Презентация для проведения мастер-класса для учителей математики

Скажи мне –

И я забуду;

Покажи мне –

И я запомню;

Дай сделать –

И я пойму.

Китайская притча

СЕМИНАР

УЧИТЕЛЕЙ

МАТЕМАТИКИ

ИСПОЛЬЗОВАНИЕ

ИНФОРМАЦИОННЫХ

ТЕХНОЛОГИЙ

НА УРОКАХ

МАТЕМАТИКИ

Информационные технологии – это совокупность методов, устройств и производственных процессов, используемых обществом для сбора, хранения, обработки и распространения информации.

« Наибольшее

значение имеет не

то, что ученик

использует новые технологии, а то,

как это использование

способствует повышению его образования»

ИКТ НА УРОКЕ

• усиливает мотивацию учения;
• дает возможность доступа к свежей информации;
• осуществляет «диалог» с источником знаний;
• экономит время;
• сочетает цвет, мультипликацию, звуковую речь, динамические модели и т.д.;
• позволяют сделать аудиторные и

самостоятельные занятия более интересными;

• предоставляют учителю большой резерв

технической и технологической поддержки.

Использование ИКТ на уроках

позволяет:

• активизировать познавательную

деятельность учащихся;

• обеспечить дифференциацию обучения;
• повысить объем работы, выполняемой на уроке;
• усовершенствовать контроль знаний;
• формировать навыки исследовательской

деятельности;

• обеспечивать доступ к различным справочным системам, электронным библиотекам и др. информационным ресурсам .

Использование компьютера в демонстрационном режиме:

~ при устном счете;

~ при объяснении нового материала;

~ при проверке домашнего задания;

~ при работе над ошибками .

Использование компьютера в индивидуальном режиме:

~ при закреплении материала;

~ при тренировке;

~ при отработке 3УН;

~ при повторении;

~ при контроле;

~ в исследовательской деятельности.

УРОКИ С

ПРИМЕНЕНИЕМ ИКТ

Уроки демонстрационного типа

Уроки тренинга или конструирования

Уроки компьютерного тестирования

С использованием

С использованием интерактивной доски

ресурсов интернет

УРОКИ ДЕМОНСТРАЦИОННОГО ТИПА

«ЗНАНИЯ БУДУТ ТЕМ ПРОЧНЕЕ И ПОЛНЕЕ,

ЧЕМ БОЛЬШИМ

КОЛИЧЕСТВОМ ОРГАНОВ ЧУВСТВ

ОНИ ВОСПРИНИМАЮТСЯ»

К.Д. УШИНСКИЙ

Внеклассное занятие по математике

РАЗРЕЗАНИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР НА ЧАСТИ

Учитель математики сош № 17

Кашенцева М.А.

ЗАДАЧИ НА РАЗРЕЗАНИЯ

Теорема Бойяи-Гервина гласит: любой многоугольник можно так разрезать на части, что из этих частей удастся сложить квадрат.

ЗАДАНИЕ 1

Разрежьте прямоугольник a ˟ 2a на такие части, чтобы из них можно было составить квадрат.

РЕШЕНИЕ ЗАДАНИЯ 1

Прямоугольник ABCD разрежем на три части по линиям MD и MC

(М – середина АВ)

РЕШЕНИЕ ЗАДАНИЯ 1

Треугольник АMD переместим так, чтобы вершина М совместилась с вершиной С, катет АМ переместится на отрезок DС.

Треугольник МВС переместим влево и вниз так, что катет МВ наложится на половину отрезка DС

РЕШЕНИЕ ЗАДАНИЯ 1

Треугольник АMD переместим так, чтобы вершина М совместилась с вершиной С, катет АМ переместится на отрезок DС.

Треугольник МВС переместим влево и вниз так, что катет МВ наложится на половину отрезка DС

ЗАДАНИЕ 2

РАЗРЕЗАТЬ РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК НА ЧАСТИ ТАК, ЧТОБЫ ИЗ НИХ МОЖНО БЫЛО СЛОЖИТЬ КВАДРАТ

РЕШЕНИЕ ЗАДАНИЯ 2

Обозначим данный правильный треугольник АВС. Необходимо разрезать ∆АВС на многоугольники так, чтобы из них можно было сложить квадрат. Тогда эти многоугольники должны иметь по крайней мере по одному прямому углу.

Пусть К – середина СВ, Т – середина АВ, точки М и Е выберем на стороне АС так, что МЕ=АТ=ТВ=ВК=СК= а , АМ=ЕС= а /2.

Проведем отрезок МК и перпендикулярные к нему отрезки ЕР и ТН.

РЕШЕНИЕ ЗАДАНИЯ 2

Разрежем треугольник на части вдоль построенных линий:

РЕШЕНИЕ ЗАДАНИЯ 2

Четырехугольник КРЕС повернем по часовой стрелке относительно вершины К так, что СК совместится с отрезком КВ.

Четырехугольник АМНТ повернем по часовой стрелке относительно вершины Т так, что АТ совместится с ТВ.

Треугольник МЕР переместим так, что в результате получится квадрат:

РЕШЕНИЕ ЗАДАНИЯ 2

РЕШЕНИЕ ЗАДАНИЯ 2

ЗАДАНИЕ 3

РАЗРЕЗАТЬ КВАДРАТ НА ЧАСТИ ТАК, ЧТОБЫ ИЗ НИХ МОЖНО БЫЛО СЛОЖИТЬ ДВА КВАДРАТА.

РЕШЕНИЕ ЗАДАНИЯ 3

ОБОЗНАЧИМ ИСХОДНЫЙ КВАДРАТ ABCD. ОТМЕТИМ СЕРЕДИНЫ СТОРОН КВАДРАТА – ТОЧКИ M, N, K, H . ПРОВЕДЕМ ОТРЕЗКИ МТ, НЕ, КF И NР – ЧАСТИ ОТРЕЗКОВ МС, НВ, КА И ND СООТВЕТСТВЕННО.

РАЗРЕЗАВ КВАДРАТ ABCD ПО ПРОВЕДЕННЫМ ЛИНИЯМ, ПОЛУЧИМ КВАДРАТ PTEF И ЧЕТЫРЕ ЧЕТЫРЕХУГОЛЬНИКА MDHT, HCKE , KBNF И NAMP .

РЕШЕНИЕ ЗАДАНИЯ 3

PTEF – УЖЕ ГОТОВЫЙ КВАДРАТ.

ИЗ ОСТАВШИХСЯ ЧЕТЫРЕХУГОЛЬНИКОВ СОСТАВИМ ВТОРОЙ КВАДРАТ.

РЕШЕНИЕ ЗАДАНИЯ 3

ВЕРШИНЫ A, B, C И D СОВМЕСТИМ В ОДНУ ТОЧКУ, ОТРЕЗКИ АМ И ВК, MD И КС, BN И СН, DH И АN СОВМЕСТЯТСЯ .

Т ОЧКИ Р, Т, Е И F СТАНУТ ВЕРШИНАМИ НОВОГО КВАДРАТА .

УРОКИ КОМПЬЮТЕРНОГО

ТЕСТИРОВАНИЯ

УРОКИ КОМПЬЮТЕРНОГО

ТЕСТИРОВАНИЯ

• ТЕСТОВЫЕ ПРОГРАММЫ ПОЗВОЛЯЮТ БЫСТРО ОЦЕНИВАТЬ РЕЗУЛЬТАТ РАБОТЫ;
• ТОЧНО ОПРЕДЕЛИТЬ ТЕМЫ, В КОТОРЫХ ЕСТЬ ПРОБЕЛЫ В ЗНАНИЯХ;
• ПРИ РЕШЕНИИ ТЕСТОВ УЧЕНИК ПОЛУЧАЕТ ОБЪЕКТИВНУЮ ОЦЕНКУ ЗНАНИЙ И УМЕНИЙ.

• КОНФИДЕНЦИАЛЬНОСТЬ РЕЗУЛЬТАТОВ БЛАГОПРИЯТНО СКАЗЫВАЕТСЯ НА ПСИХИЧЕСКОМ ЗДОРОВЬЕ РЕБЕНКА

УРОКИ С ИСПОЛЬЗОВАНИЕМ

ИНТЕРНЕТА

• свободный выход в глобальную сеть;
• возможность быстро найти

нужную информацию;

• возможность проверить свои знания.

РАБОТА С ИНТЕРАКТИВНОЙ

ДОСКОЙ

Интерактивная доска – способ организации учебного процесса, когда используемые формы, методы и средства стимулируют учебный процесс, учитывая индивидуальные особенности учащихся.

ИНТЕРАКТИВНАЯ ДОСКА -

• Заменитель обычной доски;
• Сенсорный монитор для подключенного ПК;
• Имеет собственное программное обеспечение.

УРОКИ ТРЕНИНГА

ИЛИ КОНСТРУИРОВАНИЯ

Программным обеспечением является компьютерная среда, позволяющая решать определенный тип задач. Учащиеся индивидуально или в группах работают с некоторой конструктивной средой с целью отработки навыка в решении задач или достижения какой-то учебной цели.

В любой деятельности есть:

то, что делает ее содержательной, то есть

ПРЕДМЕТНАЯ составляющая;

то, что делает ее осознанной и ответственной,

то есть МЕТАПРЕДМЕТНАЯ составляющая.

МЕТАПРЕДМЕТНАЯ составляющая деятельности « ОБУЧАЮСЬ » :

• Стратегическая
• Исследовательская
• Проектировочная
• Моделирующая
• Конструирующая
• Прогнозирующая

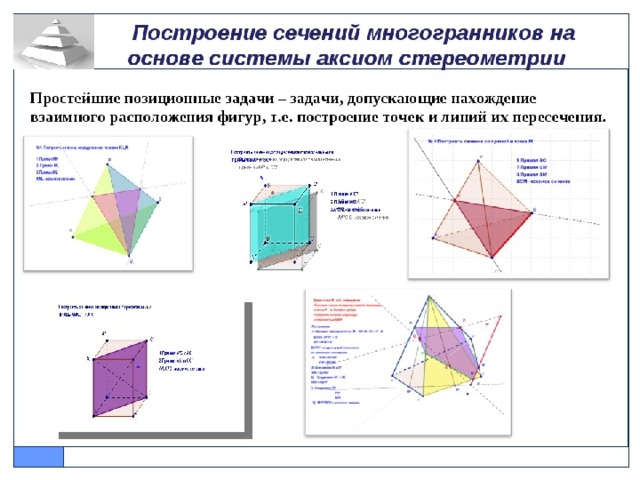
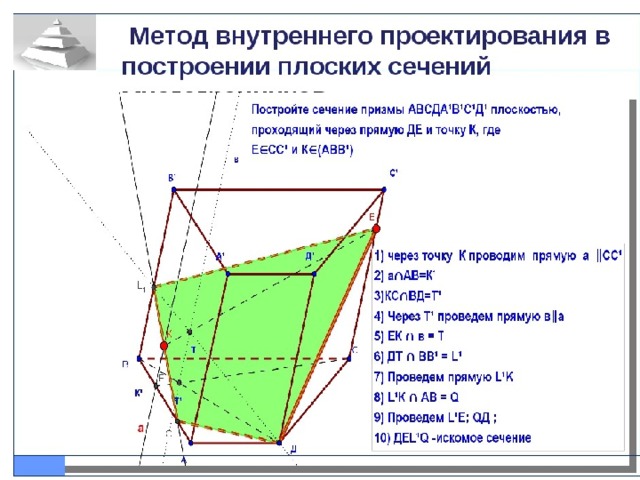
Методические особенности программы « Geogebra»

• Может использоваться как дома, так и в школе при различных формах проведения занятий и при различной компьютерной оснащенности учебного класса.
• Позволяет оптимизировать учебный процесс, более рационально используя время на различных этапах урока.
• Помогает осуществлять дифференцированный подход в обучении и проводить индивидуальную работу, используя персональные компьютеры;
• Расширяет кругозор учащихся,
• Способствует развитию познавательной активности учащихся.
• Позволяет быстрее и эффективнее освоить школьный курс по математике, повышает запоминаемость материала.
• Обеспечивает возможность изучения математики на основе деятельностного подхода за счет внедрения элементов эксперимента и исследования в учебный процесс. Повышает степень эмоциональной вовлеченности учащихся в занятия математикой, обеспечивает возможность постановки творческих задач и организации проектной работы.
• Демонстрирует, как современные технологии эффективно применяются для моделирования и визуализации математических понятий.

ВКЮЧЕНИЕ В ХОД УРОКА ИКТ

ДЕЛАЕТ ПРОЦЕСС ОБУЧЕНИЯ ИНТЕРЕСНЫМ, ЗАНИМАТЕЛЬНЫМ, СОЗДАЕТ У ДЕТЕЙ БОДРОЕ,

РАБОЧЕЕ НАСТРОЕНИЕ, ОБЛЕГЧАЕТ ПРЕОДОЛЕНИЕ ТРУДНОСТЕЙ

В УСВОЕНИИ УЧЕБНОГО МАТЕРИАЛА.

ВПЕЧАТЛЕНИЯ О

МАСТЕР-КЛАССЕ

ДО СВИДАНИЯ!

УСПЕХОВ, УДАЧИ!