Презентация к исследовательской работе "Числа Фибоначчи".

Высшее назначение математики … состоит в том, чтобы находить скрытый порядок в хаосе, который нас окружает.

Винер Н.

Числа Фибоначчи

1

1

2

3

8

13

21

5

. . .

Научный руководитель : Шелковская Елена Евгеньевна, ГБОУ РО ДККК.

Выполнили: Бочков Иван, Линьков Артем.

• Цель исследования:

• изучить проявление чисел Фибоначчи и связанного с ним закона золотого сечения, спираль в строении живых и неживых объектов,
• найти примеры использования чисел Фибоначчи.

• Задачи работы:

• Описать способ построения ряда Фибоначчи и спирали Фибоначчи.
• Увидеть математические закономерности, в строении человека, растительного мира и неживой природы с точки зрения феномена Золотого сечения.

Величайшим математиком Европы в средние века был Леонардо из Пизы, в современности он больше известен как Фибоначчи.

Леонардо Пизанский

(Фибоначчи)

Около 1175— 1250 г.

Его отец был купцом, и Леонардо много путешествовал с ним. В путешествиях он получил те знания, которые помогли ему в дальнейшей работе.

От арабов Леонардо узнал о существовании индийской, а ныне «арабской» десятичной системы счисления с ее позиционными обозначениями и нулем.

Арабская система счисления

0 1 2 3 4 5 6 7 8 9

Римская система счисления

В своем известном труде «Книга об абаке» Фибоначчи показывает превосходство десятичной системы над римской.

Памятник Леонардо

Числа Фибоначчи

• 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…

• Каждое следующее число, начиная с третьего, равно сумме двух предыдущих.
• Отношение числа ряда Фибоначчи к предыдущему стремится к Ф =1,618 :

3:2= 1,500…

1:1=1

5:3=1,666

2:1 =2,000

8:5 = 1,600

13:8= 1,625.

21:13=1,615...

• . Квадрат любого члена последовательности Фибоначчи равняется числу, которое стоит перед ним в последовательности, умноженному на то число, что идет следом за ним, плюс или минус1.
• 5 2 =(3x8)+1 8 2 =(5x13)–1 13 2  = (8 x 21) + 1…

Задача про кроликов

- пара, не дающая потомство

- пара, дающая потомство

Фибоначчи открыл свой знаменитый ряд, размышляя над задачей о количестве кроликов, которые в течении одного года должны родиться от одной пары. Он рассматривал развитие идеализированной (т.е. биологически нереальной) популяции кроликов, учитывая то, что каждая пара кроликов порождает ещё две пары на протяжении жизни, а затем погибает.

Можно заметить закономерность, которая выполняется с третьего месяца:

1

1-й месяц

3-й месяц – 1 + 1 = 2 пары;

4-й месяц – 1 + 2 = 3 пары;

5-й месяц – 2 + 3 = 5 пар;

6-й месяц – 3 + 5 = 8 пар и т.д.

2-й месяц

1

3-й месяц

2

4-й месяц

3

5-й месяц

5

6-й месяц

8

Числа Фибоначчи в природе.

Золотое сечение.

• Золотое сечение - это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей, или, другими словами, меньший отрезок так относится к большему, как больший ко всему. Прямоугольник с именно таким отношением сторон стали называть золотым прямоугольником. Его длинные стороны соотносятся с короткими сторонами в соотношении 1,168 : 1.

Спираль Фибоначчи.

233

89

144

144

13

21

55

34

На многих шишках «чешуйки» расположены в трех спиралях, полого навивающихся на стержень шишки.

• Хорошо видны эти же спирали и на ананасах: обычно их бывает 8 и 13.

Спираль и числа Фибоначчи

Гёте называл спираль «кривая жизни». Он был не только великим поэтом, но и естествоиспытателем, считал спиральность одним из характерных признаков всех организмов, проявлением самой сокровенной сущности жизни.

Если посмотреть на многие кактусы сверху, то можно и здесь обнаружить ту же спираль. Усики огурца или свернувшийся лист, бутоны цветов, брокколи также демонстрируют спиралеобразное строение.

• Нас удивляет и восхищает спиральное строение ракушек. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см. Форма спирально завитой раковины привлекла внимание Архимеда. Дело в том, что отношение измерений завитков раковины постоянно и равно 1.618. Увеличение ее шага всегда равномерно.

• В животном мире мы также можем найти множество примеров спиралей. В форме спирали развиваются рога и бивни животных, хвосты ящериц, когти львов и клювы попугаев являют собой логарифмические формы и напоминают форму оси, склонной обратиться в спираль. Паук плетёт свою паутину по спирали.

Можно увидеть спираль и в разных явлениях природы, например, таких как: смерч, ураган, облака, морские волны. Наша галактика – это спираль.

Пропорции человеческого тела.

Интересные закономерности наблюдаются, если связывать золотое сечение, числа Фибоначчи и строение человеческого тела.

Пропорции мужского тела колеблются в пределах среднего отношения 13:8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8: 5 = 1,6.

• Оказывается, спираль Фибоначчи есть и на отпечатке пальца, и в ладошках. С помощью спиралей мы слышим, во внутреннем ухе есть орган Cochlea «Улитка».

• Молекула ДНК состоит из двух вертикально переплетенных между собой спиралей. Длина каждой из этих спиралей составляет 34 ангстрема, ширина 21 ангстрема.

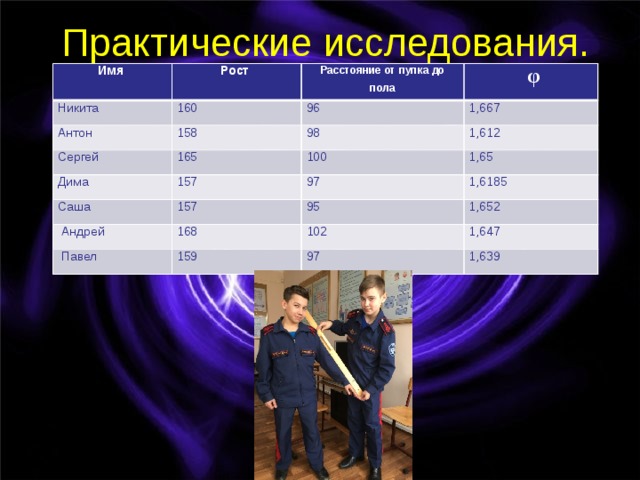
Практические исследования.

Имя

Рост

Никита

Расстояние от пупка до пола

160

Антон

Сергей

φ

96

158

165

Дима

98

1,667

1,612

100

157

Саша

1,65

97

157

Андрей

95

1,6185

168

Павел

1,652

102

159

1,647

97

1,639

Ваня.

Высота лица 16,2

ширина лица 12

высота лица 16,2

1,35

расстояние от кончика подбородка до центральной точки соединения губ 4,3

ширина рта 4,5

3,76

ширина носа3

ширина носа 3

расстояние между зрачками 5,5

1,5

расстояние между ноздрями 2,5

Артем.

расстояние между бровями 2,3

1,2

Высота лица 16,1

2,39

высота лица 16,1

ширина лица 11,8

ширина рта 4,5

расстояние от кончика подбородка до центральной точки соединения губ 4,2

1,36

3,8

ширина носа 3

ширина носа 3

1,5

расстояние между ноздрями 1,8

расстояние между зрачками 5,5

1,67

расстояние между бровями3,3

1,67

а) фуражка министра обороны РФ имеет отношение указанных частей 21,73 к 15,52, равное 1,4. б) фуражка пограничника РБ имеет размеры указанных частей 44,42 к 21,33 , что равно 2,1. в) фуражка времен СССР имеет размеры указанных частей 49,67 к 31,04, что равно 1,6. Казачья фуражка нашего офицера имеет размеры 10 к 6, что равно 1,7

Заключение

В своей исследовательской работе мы описали числа Леонардо Фибоначчи, их закономерность и историю создания. Мы убедились в том, что ряд Фибоначчи действительно очень важен для нас в изучении математики. Последовательностью ряда Фибоначчи можно объяснить многое.