Презентация к открытому уроку по теме: "Четырехугольники".

Ромб

Ромб - это параллелограмм, у которого все стороны равны.

Свойства

B

B

B

B

C

A

A

C

C

A

C

A

E

E

D

D

D

D

• 1. Противоположные углы равны
• 2. Диагонали точкой пересечения делятся пополам (BE=ED, AE=EC)
• 3. Диагонали взаимно перпендикулярны ( AC BD)
• 4. Диагонали делят углы пополам ( L ABE= L EBC, L ADE= L EDC, L BAE= L EAD, L BCE= L ECD).

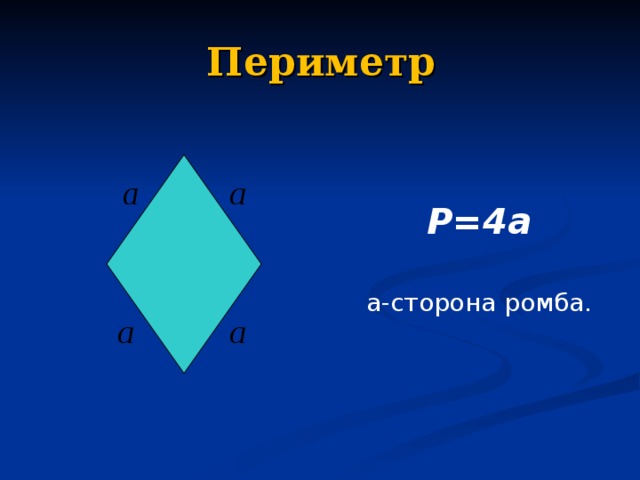
Периметр

P=4a

a- сторона ромба.

Ромб в жизни

Ромб может встречаться в жизни:

на стене в виде часов ,на стене на рисунке обоев , иногда плитка на кухне и на улице перед магазинами, на кофтах и варежках ,

на дверях, на значках футбольных команд.

Домкрат

Фигура военных летчиков

Ромб используют, как знак автомобилей

Устные задачи с ромбом

Угол B равен 150 градусов.

Найти остальные углы ромба.

Сторона AD =17см.

Найти другие стороны ромба.

Прямоугольник

B C

A D

Прямоугольник так называется, потому что у него все углы прямые.

Определение

Прямоугольник – это параллелограмм, у

которого все углы прямые

L A= L B= L C= L D=90°

B C

A D

Свойства

1. Противоположные стороны прямоугольника равны:

AD=BC, AB=CD

2. Диагонали прямоугольника равны:

AC=BD

3. Диагонали прямоугольника точкой пересечения делятся пополам:

AO=OC, BO=OD

1. 2. 3.

B C B C B C

A D A D A D

О

Формула для нахождения периметра прямоугольника

P=2(a+b)

P ABCD =2(AB+AD)

B 5см C

4см 4см

A 5см D

P ABCD =2( 4+5)=18см

Формула для нахождения площади прямоугольника

S = a · b

S ABCD =AB· BC

B 5см C

4 см

A D

S ABCD =4· 5=20 см

2

Прямоугольники в жизни

1. За основу строительства дома берут прямоугольник

2. Двери нашей школы

3. Бетонные плиты

4. Окна в доме

5. Флаг

6. Картины

7. Книги

8. Фотоаппарат

И многое другое……..

Задания для устной работы по периметру прямоугольника

№ 1

B 7 см C

3см

A D

Дано : BC=7 см, CD=3 см.

Найти : P ABCD

№ 2

B C

6см

A 2 см D

Дано: АВ=6см, AD=2 см.

Найти: P ABCD

Задания для устной работы по площади прямоугольника

№ 1

B 8 см C

3см

A D

Дано: AB=3 см , BC= 8см

Найти: S ABCD

№ 2

B C

9см

A 6 см D

Дано: CD=9 см, AD=6 см

Найти: S ABCD

Квадрат

Квадрат – это прямоугольник, у которого все стороны равны.

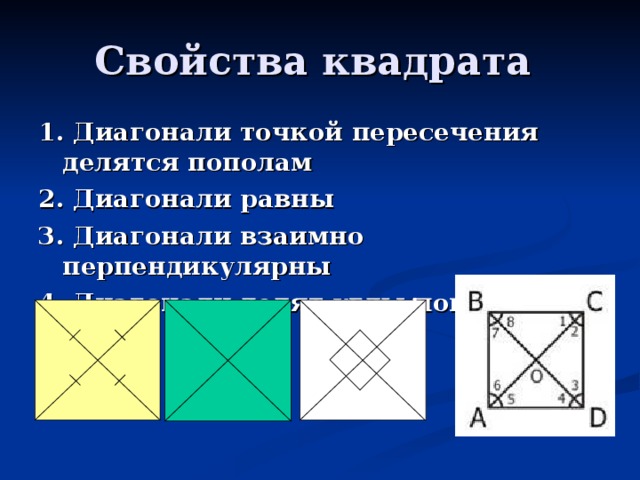
Свойства квадрата

1. Диагонали точкой пересечения делятся пополам

2. Диагонали равны

3. Диагонали взаимно перпендикулярны

4. Диагонали делят углы пополам

Периметр квадрата

Формула для нахождения периметра квадрата:

P=4a

a

Площадь квадрата

Формула для нахождения площади квадрата:

S=a²

a

Квадрат среди нас

Экран телевизора

Часы

Тарелки

Сколько квадратов изображено на рисунке?

По данным на рисунке найдите:

1) стороны квадрата ;

2) диагонали квадрата ;

3) периметр квадрата ;

4) площадь квадрата.

B 5 см C

3,5 см

A D

Трапеция

• Трапеция – это четырёхугольник, у которого две стороны параллельны, а две другие нет.

B

C

AD ll BC , AB ll CD

А

D

Элементы трапеции

основание

Боковая сторона

B

C

А

D

Боковая сторона

основание

AD, BC – основания,

AB, CD – боковые стороны

Виды трапеций

прямоугольная

равнобедренная

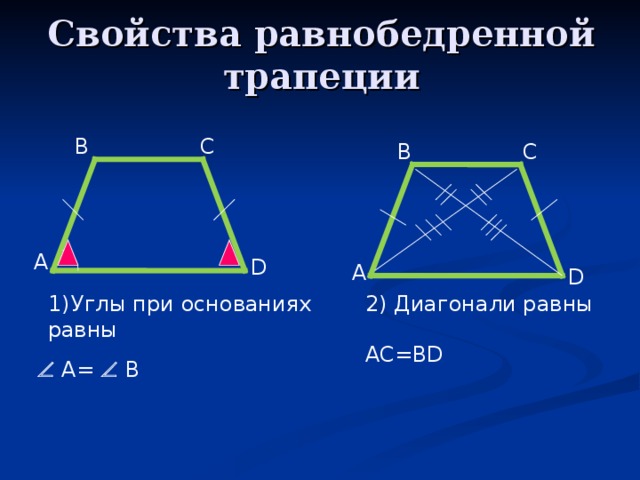
Свойства равнобедренной трапеции

B

C

C

B

А

D

А

D

• Углы при основаниях

2) Диагонали равны

AC=BD

равны

 A=  B

Средняя линия трапеции

Средняя линия трапеции –

отрезок, соединяющий середины боковых сторон

A

B

F

K

C

D

FK – средняя линия

Средняя линия трапеции равна полусумме её оснований.

FK=(AB+DC)/2

Применение формы трапеции в повседневной жизни

Стол в виде трапеции.

Подарочная упаковка, где за основу взята фигура трапеция.

Сумка в форме трапеции.

B 10 см C

M X N

A 4 см D

По данным на рис.

найдите отрезок Х

Спасибо за урок!