Презентация к проекту "Теорема Морли"

МАОУ "Лицей №14 Заслуженного учителя Российской Федерации А.М.Кузьмина

Индивидуальный проект

  Тема проекта:

Теорема Морлея

Проект сделан учеником 10-А класса Березняком Андреем Александровичем

Руководитель:  Андрющенко Алла Рудольфовна

Актуальность

Огромное количество работ по геометрии треугольника, проведённое до начала 20 века, создало впечатление, что о треугольнике уже известно всё. Тем необычнее было открытие ещё одного интересного свойства треугольника, сделанное в начале XX века известным математиком Франком Морлеем.

Цели

Изучение теоремы Морлея, областей ее применения в решении задач, написание пособия для ее изучения.

Задачи

• Изучить историю открытия теоремы Морлея
• Изучить способы доказательства теоремы
• Проанализировать область ее применения при решении различных задач
• Создать теоретико-практическое пособие по изучению теоремы Морлея

Краткая биография  Фрэнка Морлея

Франк Морлей (9 сентября 1860 — 17 октября 1937) — математик, внёсший большой вклад в алгебру и геометрию. Родился в городке Вудбридж в графстве Саффолк. Родители владели небольшим магазином фарфора. В 1884 году окончил Кингс-колледж в Кембридже, в 1887 году уехал в США, но оставался британским подданным. До 1900 года преподавал в Хэверфордском колледже (Пенсильвания), потом получил кафедру в Университете Джонса Хопкинса в Балтиморе. Был широко известен как математик, в 1919—1920 годах был президентом Американского математического общества, а с 1900 по 1921 год — редактором ведущего математического журнала American Journal of Mathematics.

История теоремы Морлея

Доказательство теоремы о трисектрисах Морлей опубликовал в 1914 году – через 15 лет после того, как нашел его. В 1924 году он изложил это доказательство более подробно и существенно усилил первоначальный результат. Доказательство Морлея весьма элегантно, но в то же время достаточно сложно. Оно базируется на рассмотрении довольно изысканных линий – так называемых кардиоид

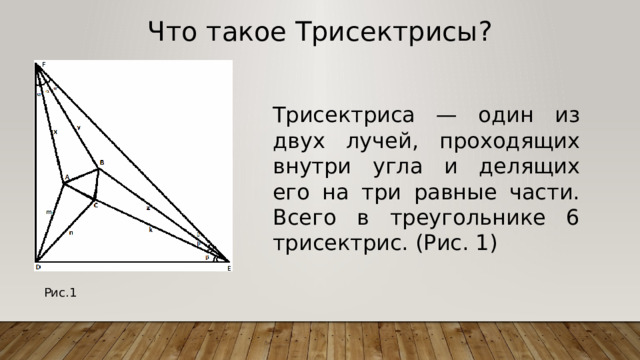
Что такое Трисектрисы?

Трисектриса — один из двух лучей, проходящих внутри угла и делящих его на три равные части. Всего в треугольнике 6 трисектрис. (Рис. 1)

Рис.1

Краткое доказательство теоремы Морлея

Доказательство Конвея

Пусть углы исходного треугольника равны 3α, 3β, 3γ. Введем удобное обозначение: будем писать ϕ ∗  вместо ϕ + 60°. Тогда α + β + γ = 0 ∗ . Заметим, что существуют треугольники с углами (0 ∗ , 0 ∗ , 0 ∗ ), (α, β ∗ , γ ∗ ), (α ∗ , β, γ ∗ ), (α ∗ , β ∗ , γ), (α ∗∗ , β, γ), (α, β ∗∗ , γ), (α, β, γ ∗∗ ), так как в каждом случае сумма углов равна 180°. Теперь для каждой тройки углов построим конкретный треугольник с этими углами, специально подбирая длины сторон. Для тройки (0∗, 0∗, 0∗) это будет равносторонний треугольник со стороной 1.

Для тройки (α ∗ , β, γ ∗ ) – это треугольник, в котором сторона, соединяющая вершины с углами α ∗  и γ ∗ , равна 1 (рис.2, а). Аналогично поступим с тройками (α, β ∗ , γ ∗ ) и (α ∗ , β ∗ , γ).

Доказательство

Для тройки (α ∗∗ , β, γ) сделаем так. Рассмотрим треугольник BXC (рис.2, б), в котором угол при вершине B равен β, при вершине X равен α ∗∗ , а при вершине C равен γ. Через вершину X проведем два луча, которые пересекают прямую BC в точках Y и Z под углом α ∗ , и подберем масштаб так, чтобы XY = XZ = 1. При этом сторона BX окажется равной стороне, лежащей против угла α ∗  в уже построенном треугольнике с углами α ∗ , β, γ ∗ . Аналогично построим треугольники и для двух оставшихся троек такого вида.

Рис 2

Доказательство

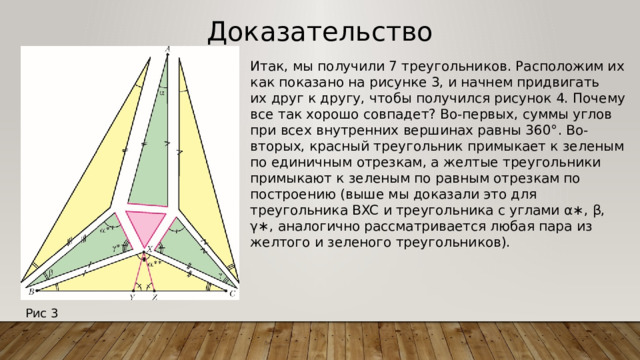
Итак, мы получили 7 треугольников. Расположим их как показано на рисунке 3, и начнем придвигать их друг к другу, чтобы получился рисунок 4. Почему все так хорошо совпадет? Во-первых, суммы углов при всех внутренних вершинах равны 360°. Во-вторых, красный треугольник примыкает к зеленым по единичным отрезкам, а желтые треугольники примыкают к зеленым по равным отрезкам по построению (выше мы доказали это для треугольника BXC и треугольника с углами α∗, β, γ∗, аналогично рассматривается любая пара из желтого и зеленого треугольников).

Рис 3

Доказательство

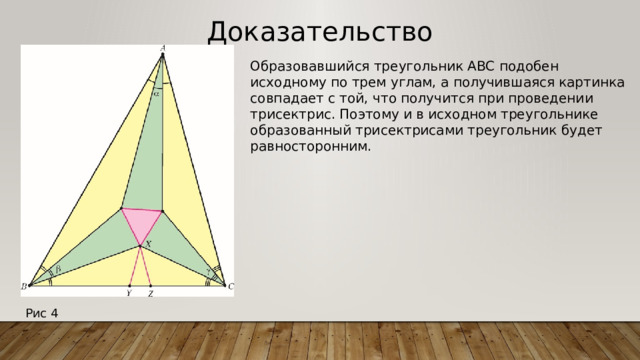
Образовавшийся треугольник ABC подобен исходному по трем углам, а получившаяся картинка совпадает с той, что получится при проведении трисектрис. Поэтому и в исходном треугольнике образованный трисектрисами треугольник будет равносторонним. 

Рис 4

Применение теоремы Морлея при решении задач

Дано: ΔABC, AZ, CZ, AQ, BQ, CD, BD трисектрисы, QD=12.

Найти: SΔZQD

Решение:

1)По теореме Морли ΔZQD равносторонний так как AZ, CZ, AQ, BQ, CD, BD трисектрисы.

2)По формуле площади равностороннего треугольника S=√3 * QD /4=√3

Ответ:36√3

Применение теоремы Морлея при решении задач

Дано: ΔABC равносторонний, AZ, CZ, AQ, BQ, CD, BD трисектрисы.

Доказать: ΔAZQ=ΔBQD= ΔCZD.

Решение:

1)Так как ΔABC равносторонний, то все углы, образованные трисектрисами равны. Следовательно, ZAC=ZAQ=QAB=ZCA=ZCD=DCB=CBD=DBQ=QBA

2)Рассмотрим ΔAZC, ΔBQA и ΔCDB они равны так как AC=AB=BC по свойству равностороннего треугольника

ZAC=ZAQ=QAB=ZCA=ZCD=DCB=CBD=DBQ=QBA Следовательно, ΔAZC=ΔBQA=ΔCDB

3)ΔAZC=ΔBQA=ΔCDB следует AZ=ZC=AQ=BQ=DB=CD

4)Рассмотрим ΔAZQ, ΔBQD и ΔCZD

AZ=ZC=AQ=BQ=DB=CD

AC=AB=BC по свойству равностороннего треугольника

Следовательно, ΔAZQ=ΔBQD= ΔCZD.

Выводы

В результате выполнения работы была достигнута поставленная цель изучить одну из самых элегантных теорем геометрии - теорему Морлея. Была исследована история открытия этой теоремы. Рассмотрены несколько современных вариантов ее доказательства. На различных задачах были исследованы возможности практического применения данной теоремы. 

Полученные результаты позволили составить теоретико-практическое пособие для школьников по изучения данной теоремы и областей ее применения при решении геометрических задач. Поставленные в работе задачи выполнены полностью.

Проведенное исследование показало, что вопрос о трисектрисах треугольника и их свойствах изучен еще не всесторонне. Полученный продукт индивидуального проекта представляет интерес с точки зрения расширения наших знаний о математике.

Список литературы

• Морли, Фрэнк [Электронный ресурс] : Материал из Википедии — свободной энциклопедии : Версия 108162001, сохранённая в 10:39 UTC 13 июля 2020 / Авторы Википедии // Википедия, свободная энциклопедия. — Электрон. дан. — Сан-Франциско: Фонд Викимедиа, 2020. — Режим доступа: https://ru.wikipedia.org/?curid=655628&oldid=108162001
• Тоноян Г., Яглом И. , Теорема Морлея. «Квант», №8, 1978
• Л. Штейнгарц, Снова о теореме Морлея. «Квант», №5, 2009
• Простой и неисчерпаемый треугольник. Режим доступа:  http://www.microanswers.ru/article/prostoj-i-neischerpaemij-treygolnik.html