Презентация к уроку по алгебре и началам анализа 11 класс на тему: " Применение производной в различных областях науки"

«Применение производной в различных областях науки» Омарова Заира Насруллаевна МКОУ «СОШ№11» г.Избербаш РД

Цели урока :

• Добиться усвоения учащимися систематических, осознанных сведений о понятии производной, её геометрическом и физическом смысле.
• Показать межпредметную связь на примере математического моделирования.
• Показать применение производной при решении жизненно важных задач.

ПРОБЛЕМНЫЙ ВОПРОС

Действительно ли это так?

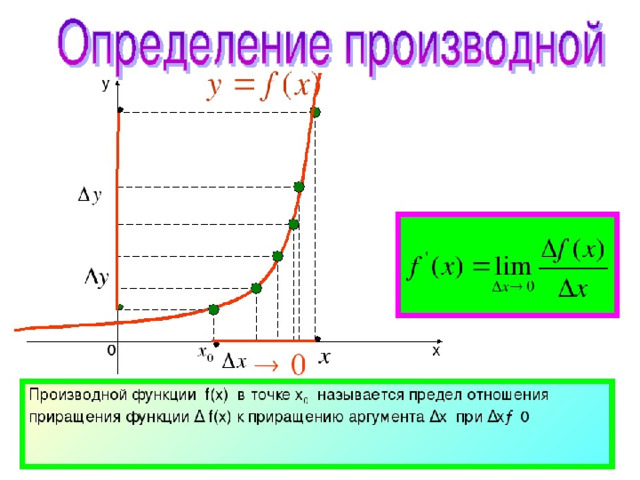
Что необходимо знать для нахождения производной? Правила дифференцирования и таблицу производных.  Вспомни!

Функция

Производная

kx+m

Функция Производная

c,c - cons t

1

ctg x

- sin x

2x

k* f (x)

f '(x)+ g '(x)

sin x

f (x)* g (x)

А

Повторение

4

tg A-?

Tg A=7/4

В

С

7

А

tg В -?

Tg B=4/7

Вычислите tgα, если

α = 135°, 120°, 150°.

В

С

3

 =-  3

 =-  3/3

 =-1

Повторение

Угловой коэффициент прямой.

Прямая проходит через начало

координат и точку Р(3; -1). Чему

равен ее угловой коэффициент?

y=kx+b

y=kx

Найдите угловые коэффициенты прямых:

Повторение

k=0,5

1

k=3

2

k=0

3

k=-1

4

б) В чем заключается геометрический смысл производной?

Найти угловой коэффициент нормали к графику у=3х ² в точке с абсциссой х=-1.

в) В чем заключается механический (физический) смысл производной?

Подведем итоги:

• Каков физический смысл производной перемещения?
• Можно ли найти производную скорости? Используется ли эта величина в физике Как она называется?
• Мгновенная скорость равна нулю. Что можно сказать о движении тела в этот момент?
• Каков физический смысл следующих высказываний: производная движения равна нулю в точке х; при переходе через точку х производная меняет знак ?

Внимание! Пришло время поработать!

Задание 1. Заполните таблицу №1:

Задание 1. Заполни таблицу №2:

ПРОЕКТЫ УЧАЩИХСЯ.

1-я группа «Исторические сведения»

1. История возникновения производной функции

Раздел математики, в котором изучаются производные и их применение к исследованию функций, называется дифференциальным исчислением . Приращения вида Δf , представляющие собой разности, играют заметную роль при работе с производными. Естественно поэтому появление латинского корня differentia (разность) в названии calculis differentialis нового исчисления, которое переводится как исчисление разностей; это название появилось уже в конце 17в., т.е. при рождении нового метода.

Термин « производная » является буквальным переводом на русский французского слова deriveе , которое ввёл в 1797г. Ж.Лагранж , он же ввёл современные обозначения у' , f'. Такое название отражает смысл понятия: функция f'(x) происходит из f(x), является производным от f(x). И.Ньютон называл производную функцию флюксией , а саму функцию – флюентой . Г.Лейбниц говорил о дифференциальном отношении и ввёл обозначение производной df/dx .

Слово «э кстремум » происходит от латинского extremum (крайний). Maximum переводится как наибольший, а minimum – наименьший.

Жозеф Луи Лагранж

« – величественная пирамида математических наук»

Наполеон I Бонапарт

• Рано изучил сочинения Евклида и Архимеда, Галлея (друга Ньютона).
• В 16 лет стал преподавать математику в Артиллерийском училище в Турине.
• В 19 лет стал профессором математических наук.
• В 23 года стал академиком и иностранным членом Берлинской академии наук.
• Автор трудов по вариационному исчислению, математическому анализу, теории чисел, алгебре, дифференциальным уравнениям.
• Его работы по математике, астрономии и механике составляют 14 томов .
• Император Франции сделал учёного сенатором, графом империи и командором ордена Почетного легиона.

1736 - 1813

Выдающийся французский математик, ввел термин « ПРОИЗВОДНАЯ » и её современное обозначение.

II группа - «Применение физического смысла производной при решении физических задач».

3. Физический (механический) смысл производной

Исаак Ньютон

Это кто?

«Когда величина является максимальной или минимальной, в этот момент она не течет ни вперед, ни назад»

}

3. Физический (механический) смысл производной

0

s

S(t) за время t

a(t)

V’(t)

S’(t)

V(t)

=

=

S(t) - перемещение точки за время t

V(t) – скорость точки в момент t

a(t) – ускорение точки в момент t

3. Физический (механический) смысл производной

Пример: Материальная точка движется по закону

(м).

Найти

В какой момент времени (с) скорость точки будет равна 12,8 м/c ?

S’(t)

Найти

V(t)

=

Решение:

t = 2,2 (с).

3. Физический (механический) смысл производной

Пример: Точка движется прямолинейно по закону

S(t) = 2 t ³ - 3 t. Вычислите скорость движения точки:

а) в момент времени t ;

б) в момент времени t=2с .

Решение:

а)

б)

Ответ: V(t)=6t 2 -3; V(2)=21 м/с

3. Физический (механический) смысл производной

Пример: Тело, подброшенное вверх движется по закону s ( t ) = 4+ 8 t – 5 t 2 . Найдите:

1) скорость тела в начальный момент времени;

2) наибольшую высоту подъёма тела.

РЕШЕНИЕ:

1) v ( t ) = s’ ( t ) = 8 – 10 t - скорость тела;

2) t = 0, v (0) = s’ (0) = 8 м/с – скорость тела в начальный момент времени

3) s (0,8)= 4+ 8·0,8 – 5· 0,64 =7,2 м – максимальная высота броска тела.

подсказка

Ответ: 8 м/с ; 7,2 м.

В наших домах, на транспорте, на заводах : всюду работает электрический ток.

Под электрическим током понимают направленное движение свободных электрически заряженных частиц.

Количественной характеристикой электрического тока является сила тока.

В цепи электрического тока электрический заряд меняется с течением времени по закону q=q (t). Сила тока I есть производная заряда q по времени.

=q’(t)

30. При какой скорости расход горючего будет наименьший? Решение: Исследуем расход горючего с помощью производной: f '(х)=0,0034х-0,18. Тогда f'(х)=0 при х≈53. Определим знак второй производной в критической точке: f''(х)=0,00340, следовательно, расход горючего при скорости 53 км/ч будет наименьшим. f(53)≈5,43 л. " width="640"

Задача

Расход горючего легкового автомобиля (литр на 100 км) в зависимости от скорости х км/ч при движении на четвертой передаче приблизительно описывается функцией

f(x)=0,0017х 2 -0,18х+10,2; х30. При какой скорости расход горючего будет наименьший?

Решение:

Исследуем расход горючего с помощью производной:

f '(х)=0,0034х-0,18.

Тогда f'(х)=0 при х≈53.

Определим знак второй производной в критической точке: f''(х)=0,00340, следовательно, расход горючего при скорости 53 км/ч будет наименьшим. f(53)≈5,43 л.

Связь производной с биохимией

Реакция организма на введенное лекарство может выражаться в повышении кровяного давления, уменьшения температуры тела, изменении пульса или других физиологических показателей. Степень реакции зависит от назначенного лекарства, его дозы. Предположим, что Х обозначает дозу назначенного лекарства, тогда У - функция степени реакции выражается формулой y = x²(a - x), где а – биомасса. При каком значении X реакция максимальна?

Решение: 0

Тогда

Это тот уровень дозы,

который даёт

максимальную реакцию.

32

ПРОИЗВОДНАЯ

В БИОЛОГИИ

Понятие на языке биологии

Обозначение

Численность в момент времени t

Понятие на языке математики

N = N (t)

Интервал времени

Функция

∆ t = t 2 – t 1

Изменение численности популяции

Скорость изменения численности популяции

∆ N = N(t 2 ) – N(t 1 )

Приращение аргумента

Приращение функции

∆ N/∆t

Относительная скорость роста в данный момент t

Отношение приращения функции к приращению аргумента

Lim ∆N/∆t

Производная

t 0

v(t) = N′ (t)

Задача

Рассчитайте на основании имеющихся данных, как будет меняться плотность популяции синиц через год и 2 года, если плотность синиц составляет 260 особей/га. За период размножения из одной кладки яиц в среднем выживает 3 птенца.

В популяции равное число самцов и самок. Смертность синиц постоянна, в среднем за год погибает 27особей. Найти скорость роста численности популяции в год.

Вспомогательные формулы и определения для решения задачи

Популяция – это совокупность особей данного вида, занимающих определённый участок территории внутри ареала вида, свободно скрещивающихся между собой и частично или полностью изолированных от других популяций, а также является элементарной единицей эволюции.

Эффективная численность популяции – это совокупность особей, которые участвуют в воспроизведении потомства.( Ne)

Плотность популяции – это численность популяции на единицу площади.

Формула Ферсхюльца: N 1 = (Ne - К смерт )( К рожд + N 0 )

Скорость численности популяции : v(t)=N’(t)

Решение: По условию плотность популяции N 0 = 260 особей/га. В популяции равное число самцов и самок, а значит эффективная численность популяции равна 100.

Nе= 100% , тогда Nе= 1

Коэффициент смертности К смерт = 27% = 0,27

За год 130 пар дает 390 птенцов, т.е. (260/2)*3 =390

Формула N 1 = (Nе- К смерт )( К рожд + N 0 ) =

= (1-0.27)(390+260)= 474 особей всего за 1-ый год N 1

Относительный прирост численности популяции ∆N= 474/260= 1,82 раза

Тогда численность популяции будет определяться функцией : N= 260* 1,82 t где t=1,2,….

Найдем тогда скорость роста численности популяции:

  v(t)= N’(t) = (260*1.82 t )’ = 260* (1.82 t )’ =

=260*1.82 t * ln 1.82 (особей/ год)

  N(1) = 260*1.82 1 = 260*1.82= 474 особи

N(2)= 260*1.82 2 = 260*3.3124= 861 особь.

Ответ: 260*1.82 t * ln 1.82 особей/ год

Производная в химии.

Например, инженерам-технологам при определении эффективности химических производств, химикам, разрабатывающим препараты для медицины и сельского хозяйства, а также врачам и агрономам, использующим эти препараты для лечения людей и для внесения их в почву. Одни реакции проходят практически мгновенно, другие идут очень медленно. Поэтому в реальной жизни для решения производственных задач в медицинской, сельскохозяйственной и химической промышленности просто необходимо знать скорости реакций химических веществ.

Математическая модель производной в химии

Понятие на языке химии

Обозначение

Количество в-ва в момент времени t

Понятие на языке математики

p = p(t)

Интервал времени

Функция

∆ t = t 2 – t 1

Изменение количества в-ва

∆ p= p(t 2 ) – p(t 1 )

Средняя скорость химической реакции

Приращение аргумента

Приращение функции

∆ p/∆t

Отношение приращения функции к приращению аргумента

V (t) = p ‘(t)

Как используют производную в химии?

Производную в химии используют для определения очень важной вещи – скорости химической реакции, одного из решающих факторов, который нужно учитывать во многих областях

научно-производственной деятельности .

Определение

Скоростью химической реакции в химии называется изменение концентрации реагирующих веществ в единицу времени или

производная от концентрации реагирующих веществ по времени (на языке математике концентрация была бы функцией, а время – аргументом)

Формула производной в химии

Если P(t) – закон изменения количества вещества, вступившего в химическую реакцию, то скорость v(t) химической реакции в момент времени t равна производной:

V (t) = p ‘(t)

Пример задачи по химии:

Пусть количество вещества, вступившего в химическую реакцию задается зависимостью:

р(t) = t 2 /2 + 3t –3 (моль)

Найти скорость химической реакции через 3 секунды.

Решение:

р(t) = t 2 /2 + 3t –3 (моль)

1. Найдем производную функции:

Р’(t) = t +3

2. Подставим значение t = 3 сек:

P’(3) = 3 + 3 = 6 (моль/сек )

Ответ: 6 моль/сек

Заключение

Понятие производной очень важно в химии при определении скорости течения реакции.

Экономический смысл производной.

Математическая модель производной в экономике

Понятие на языке экономики

Обозначение

Количество произведенной продукции в момент времени t

Понятие на языке математики

v = v(t)

Интервал времени

Функция

∆ t = t 2 – t 1

Изменение количества произведенной продукции

∆ v= v(t 2 ) – v(t 1 )

Средняя производительность труда

Приращение аргумента

Приращение функции

∆ v/∆t

Отношение приращения функции к приращению аргумента

Производительность труда P(t) = v‘(t)

Объем продукции цеха в течение рабочего дня представляет функцию – рабочее время в часах. Вычислить максимальную производительность труда в течение рабочего дня.

Вопрос: почему после третьего часа работы мы наблюдаем спад производительности труда?

Ответ: упадок сил, плохо проветрено помещение, возможно бригада рабочих использует ручной труд.

Вывод: Экономическое приложение производной помогает как экономистам и бизнесменам, так и обычным гражданам в распоряжении бюджетом.

Выберете смайлик, соответствующий вашему настроению и состоянию после проведенного урока

тревожно, не уверен в себе

спокойно, у меня все получится

безразлично, что будет, то и будет

При создании данной презентации были использованы слайды презентаций, созданные

• учитель математики МОУ «Курлекская СОШ» Томского района Томской области
• Логунова Людмила Васильевна , 2006 год
• учитель математики высшей категории МОУ «СОШ №1», г. Магнитогорска, Пупкова Татьяна Владимировна 10 класс «А» ГБОУ СОШ №717, учитель: Чернецова Карина Игоревна
• Ковальчук Лариса Ивановна , учитель математики МОУ СОШ № 288 ЗАТО г.Заозёрск Мурманской области
• 10 класс «А» ГБОУ СОШ №717
• Дацык О.Н ., учитель математики, МОУ «Гимназия», г. Костомукша, Республика Карелия

• Амбарцумян Ануш, Дешевых Андрей, Рындин Вячеслав, Макаровская Ирина, Леликова Евгения, Морохов Александр. Задания для устного счета

• Чудаева Елена Владимировна, учитель математики, г. Инсар, Республика Мордовия

и материалы с сайта

Домашнее задание.

1. Решить самостоятельно задачи.

а) Смесь состоит из углерода (С) и алюминия (Al). Требуется найти концентрацию углерода (С), при которой содержащаяся в смеси карбида алюминия реагирует с наибольшей скоростью. б) Первоначальная численность популяции состоит из 3000 особей. Найти максимальный размер этой популяции, если ее численность р(t) возрастает по закону

, где t выражается в часах.

2. Шкиль Н. И. и др. Математика: алгебра и начала математического анализа (базовый и углублённый уровень). 10-11 кл.- К.: Зодиак-ЭКО, 2014.

§15, п. 15.1-15.3

ИНСТРУКЦИЯ К ПРАКТИЧЕСКОМУ ЗАНЯТИЮ

Группа «Биологи-исследователи»

Цель : познакомиться с особенностями исследования численности популяции, его спада или роста, и выявления причин того или иного процесса; для этого выполнить задания, записать ход решения, сделать выводы.

  Ход работы:

  Задание №1.

  В среду вносят популяцию из 1000 бактерий. Численность (p) популяции

возрастает по закону p(t)= 1000 + , где t выражается в часах.

Найти максимальный размер этой популяции и проанализировать

результат.

  Задание №2.

Рассчитайте на основании имеющихся данных, как будет меняться

плотность популяции мушек дрозофил через год и 2 года, если

плотность популяции составляет 256000 особей/га. За период

размножения из одной кладки яиц в среднем выживает 22 особи. В

популяции равное число самцов и самок. Смертность дрозофил постоянна,

в среднем за год погибает 36% особей. Найти скорость роста численности

популяции в год. Полученные данные проанализировать.

Группа «Физики-исследователи»

Цель : познакомиться со cвязью производной функции в физике, определить насколько это важно для задач практического характера; для этого выполнить задания, записать ход решения, сделать выводы.

Ход работы:

Задание №1.

  Заряд, протекающий через проводник, меняется по

закону q=sin 3 (2t-10). Найти силу тока в момент t=50 сек.

Задание №2.

Тело массой m 0 движется прямолинейно по закону

s(t)= αt 2 +βt+ γ, где α, β, γ – постоянные. Доказать, что

сила, действующая на тело, постоянна .

Группа «Химики-исследователи»

Цель : познакомиться со связью производной функции с химией; для этого выполнить задания, записать ход решения, сделать выводы.  

Ход работы:

Задание №1.

Смесь состоит из серы(S) и кислорода(O 2 ). Требуется найти

концентрацию кислорода(O 2 ), при которой сера(S) реагирует с

наибольшей скоростью.

Задание №2.

При какой концентрации азота(N 2 ) и водорода(H 2 ) реакция будет

достигать наивысшей скорости, если в результате их

взаимодействия образуется аммиак(NH 3 ).

Группа «Экономисты-исследователи»

Цель : познакомиться с особенностями исследования производственной функции , её спада или роста, и выявления причин того или иного процесса; для этого выполнить задания, записать ход решения, сделать выводы.

  Ход работы:

Задача №1

Цементный завод производит X тонн цемента в день. По договору он

должен ежедневно поставлять строительной фирме не менее 20 тонн

цемента. Производственные мощности завода таковы, что выпуск не

может превышать 90 тонн в день.

Определить:

1) при каком объёме производства удельные затраты производства будут наибольшими ( наименьшими);

2) выгодно ли строительной фирме быть единственным партнёром завода?

Функция суммарных затрат имеет вид: K(x)= - x 3 + 98x 2 + 200x

Задача №2

Пусть функция затрат при производстве

апатитового концентрата имеет вид:

К(Х)=

Определить предельные издержки

производства при увеличении объёма

выпуска на x=2 единицы и на

x=10 единиц.

Вопрос: выгодно ли данному

предприятию наращивать

производство, если уровень затрат не

изменится?