Презентация на 22 конкурс"Лучший учитель школ воспитательных колоний УИС"

« Скажи мне – и я забуду. Покажи мне- и я запомню. Вовлеки меня - и я научусь » -

древняя китайская пословица .

Историческая справка

• Термин вектор (от лат. Vector – “ несущий “) впервые появился в 1845 г. у ирландского математика Уильяма Гамильтона в работах по построению числовых систем.
• Вектор это направленный отрезок.

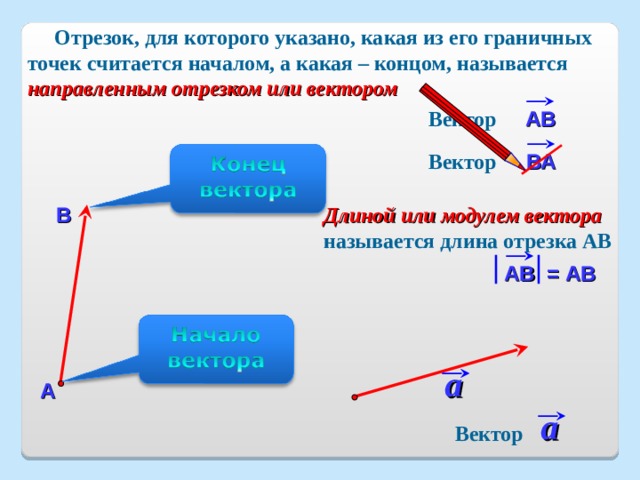
Отрезок, для которого указано, какая из его граничных точек считается началом, а какая – концом, называется направленным отрезком или вектором

Вектор

АВ

Вектор

ВА

Длиной или модулем вектора называется длина отрезка АВ

В

АВ = АВ

a

А

a

Вектор

3

Многие физические величины, например

сила, перемещение материальной точки, скорость, характеризуются не только своим числовым значением, но и направлением в пространстве. Такие физические величины называются векторными величинами ( или коротко векторами)

A

1Н

8 Н

В

4

При изучении электрических и магнитных явлений появляются новые примеры векторных величин.

Электрическое поле, создаваемое в пространстве зарядами, характеризуется в каждой точке пространства вектором напряженности электрического поля.

На рисунке изображены векторы напряженности электрического поля положительного точечного заряда.

E

+

5

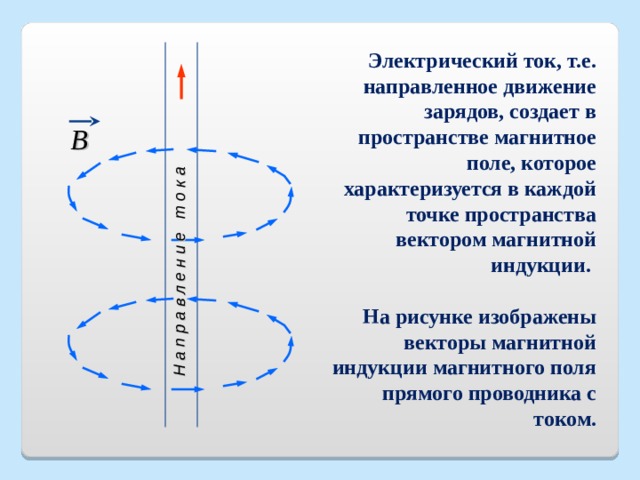
Н а п р а в л е н и е т о к а

Электрический ток, т.е. направленное движение зарядов, создает в пространстве магнитное поле, которое характеризуется в каждой точке пространства вектором магнитной индукции.

На рисунке изображены векторы магнитной индукции магнитного поля прямого проводника с током.

B

6

Сложение векторов.

Правило многоугольника.

Правило треугольника.

D

В

С

С

А

А

В

α

ABCD – пространственный многоугольник

Свойства:

- переместительный закон;

- сочетательный закон.

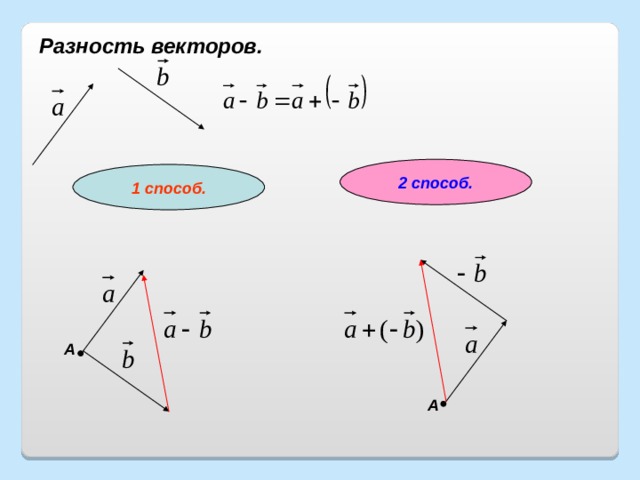
Разность векторов.

2 способ.

1 способ.

А

А

ТАКСИ

Естественно считать, что вектор 2 v получается умножением вектора v на число 2, а вектор -2 v получается умножением вектора v на число -2. Этот пример показывает каким образом следует вести умножение вектора на число и что при умножении получается вектор.

Если мы изобразим скорость первого автомобиля вектором v , то естественно изобразить скорость второго автомобиля вектором, у которого направление такое же, как у вектора v , а длина в 2 раза больше, и обозначить этот вектор 2 v . Скорость третьего автомобиля изобразиться вектором, противоположным вектору 2 v , т.е. вектором -2 v .

Прежде, чем ввести еще одно действие – умножение вектора на число, обратимся к примеру. Представим себе, что один автомобиль движется прямолинейно с постоянной скоростью, второй движется в том же направлении со скоростью, вдвое большей, а третий автомобиль движется им навстречу, т.е. в противоположном направлении, и величина его скорости такая же, как у второго автомобиля.

-2v

2v

v

«Геометрия 7-9» Л.С. Атанасян и др.

9

0 b ka «Геометрия 7-9» Л.С. Атанасян и др. 1 a 1 3 a 2 a - 2 10 " width="640"

Умножение вектора на число.

k

a

Произведением ненулевого вектора на число

называется такой вектор , длина которого равна ,

причем векторы и сонаправлены при и

притивоположно направлены при .

b

k

a

a

k0

b

k

a

«Геометрия 7-9» Л.С. Атанасян и др.

1 a

1

3 a

2

a

- 2

10

4. Умножение вектора на число.

Свойства:

- сочетательный закон

- первый распределительный закон

- второй распределительный закон

5. Если векторы и коллинеарны и , то существует число k такое, что

Назовите вектор, который получится в результате умножения.

A

N

D

C

B

F

S

E

R

M

Q

U

Y

T

V

I

P

X

G

O

K

H

J

Z

L

11

Решаем задачи

устно

Решите устно следующие задачи:

A

1.

Найдите:

3 см

3 см

M

4 см

D

5 см

B

5 см

K

N

4 см

1,5 см

C

2 см

2,5 см

Найдите k:

Дан куб.

3.

B 1

C 1

K= -1

K= 2

A 1

D 1

O

K= -

C

B

D

A

Работа

Решение задач по готовым чертежам

1. Рассмотрим первое равенство, 

.

2.Рассмотрим следующее равенство 

1. Рассмотрим первое равенство, 

.

2.Рассмотрим следующее равенство 

умею…

знаю…

Рефлексия

Закончи предложения…

Я

могу…

Домашнее

задание

Итоги урока