
Тема урока: «Некоторые следствия из аксиом стереометрии»
ЧТО ПРОХОДИЛИ НА ПРОШЛОМ УРОКЕ?
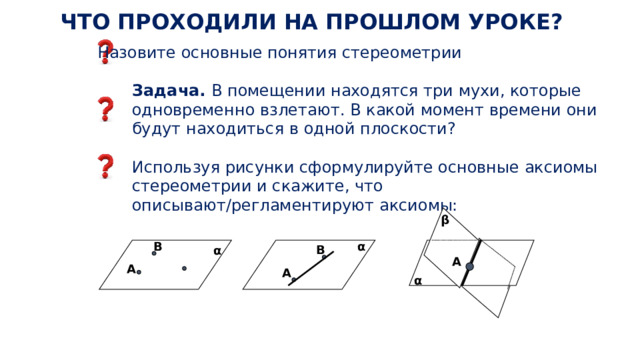
Назовите основные понятия стереометрии
Задача. В помещении находятся три мухи, которые одновременно взлетают. В какой момент времени они будут находиться в одной плоскости?
Используя рисунки сформулируйте основные аксиомы стереометрии и скажите, что описывают/регламентируют аксиомы:
β
В
α
В
α
А
А
А
α

Некоторые следствия из аксиом
Теорема 1
Через прямую и не лежащую на ней точку проходит плоскость и притом только одна.
Доказательство:
α
- Для того, чтобы доказать существование плоскости, выберем на прямой a две точки, так что:
О
Р
М
Доказать:
а
а)
По аксиоме А1: через точки Р, О, М проходит плоскость
По аксиоме А2: т.к. две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости, т.е.
2. Любая плоскость проходящая через прямую а и точку М проходит через т.Р, т.О, и т.М, значит по аксиоме А1 она – единственная.
Теорема доказана
 все точки b принадлежат плоскости . (по аксиоме А2) 5. Плоскость проходит через а и b и она единственная, т.к. любая плоскость, проходящая через прямые а и b, проходит и через Н, значит α – единственная. Теорема доказана " width="640"
все точки b принадлежат плоскости . (по аксиоме А2) 5. Плоскость проходит через а и b и она единственная, т.к. любая плоскость, проходящая через прямые а и b, проходит и через Н, значит α – единственная. Теорема доказана " width="640"
Некоторые следствия из аксиом
Теорема 2
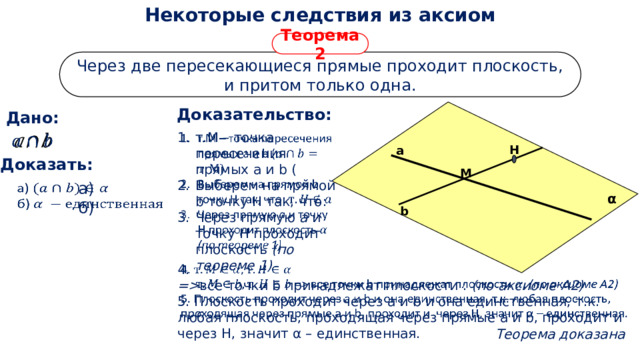
Через две пересекающиеся прямые проходит плоскость, и притом только одна.
Доказательство:
Дано:
- т.М – точка пересечения прямых a и b (
- Выберем на прямой b точку Н так, что:
- Через прямую a и точку H проходит плоскость (по теореме 1)
Н
а
Доказать:
М
а)
б)
α
b
4.
= все точки b принадлежат плоскости . (по аксиоме А2)
5. Плоскость проходит через а и b и она единственная, т.к. любая плоскость, проходящая через прямые а и b, проходит и через Н, значит α – единственная.
Теорема доказана
 С А 2. Две точки каждого отрезка лежат в плоскости, значит все точки каждого из отрезков лежат в плоскости α (по аксиоме А2) Отсюда, отрезки АВ, ВС, АС лежат в плоскости α Ч.т.д. " width="640"
С А 2. Две точки каждого отрезка лежат в плоскости, значит все точки каждого из отрезков лежат в плоскости α (по аксиоме А2) Отсюда, отрезки АВ, ВС, АС лежат в плоскости α Ч.т.д. " width="640"
РЕШАЕМ ЗАДАЧИ
№ 6
Три данные точки соединены попарно отрезками. Докажите, что все отрезки лежат в одной плоскости.
Всё ли понятно в задаче?
Можем ли мы однозначно построить чертёж?
Доказательство:
1-й случай
1. По аксиоме А1 через три точки проходит плоскость
α
В
=
С
А
2. Две точки каждого отрезка лежат в плоскости, значит все точки каждого из отрезков лежат в плоскости α (по аксиоме А2)
Отсюда, отрезки АВ, ВС, АС лежат в плоскости α
Ч.т.д.

РЕШАЕМ ЗАДАЧИ
№ 6
Три данные точки соединены попарно отрезками. Докажите, что все отрезки лежат в одной плоскости.
2-й случай
Доказательство:
Так как 3 точки принадлежат одной прямой, то все точки этой прямой лежат в плоскости.
(по аксиоме А2)
Ч.т.д.
С
В
А
α

АВСД – ромб, О – точка пересечения его диагоналей, М – точка пространства, не лежащая в плоскости ромба. Точки А, Д, О лежат в плоскости α.
Определить и обосновать:
- Лежат ли в плоскости α точки В и С?
- Лежит ли в плоскости МОВ точка Д?
- Назовите линию пересечения плоскостей МОВ и АДО.
- Вычислите площадь ромба, если сторона его равна 4 см, а угол равен 60º. Предложите различные способы вычисления площади ромба.
М
В
С
О
D
А
 С В Докажите самостоятельно, что О D А " width="640"
С В Докажите самостоятельно, что О D А " width="640"
АВСД – ромб, О – точка пересечения его диагоналей, М – точка пространства, не лежащая в плоскости ромба. Точки А, Д, О лежат в плоскости α.
Определить и обосновать:
- Лежат ли в плоскости α точки В и С?
М
Доказательство:
=
С
В
Докажите самостоятельно, что
О
D
А
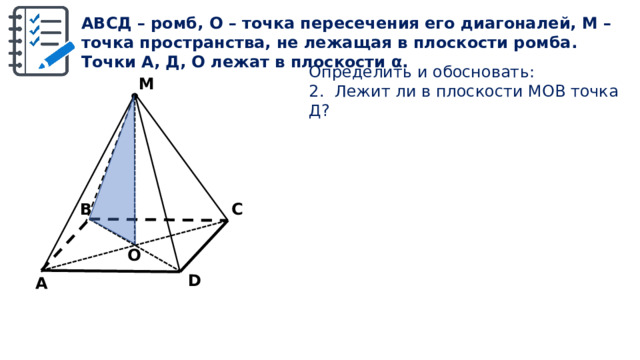
АВСД – ромб, О – точка пересечения его диагоналей, М – точка пространства, не лежащая в плоскости ромба. Точки А, Д, О лежат в плоскости α.
Определить и обосновать:
2. Лежит ли в плоскости МОВ точка Д?
М
В
С
О
D
А

АВСД – ромб, О – точка пересечения его диагоналей, М – точка пространства, не лежащая в плоскости ромба. Точки А, Д, О лежат в плоскости α.
Определить и обосновать:
3. Назовите линию пересечения плоскостей МОВ и АДО.
М
Ответ: BD
С
В
О
D
А

АВСД – ромб, О – точка пересечения его диагоналей, М – точка пространства, не лежащая в плоскости ромба. Точки А, Д, О лежат в плоскости α.
4. Вычислите площадь ромба, если сторона его равна 4 см, а угол равен 60º. Предложите различные способы вычисления площади ромба.
В
4
Какую геометрическую фигуру называют ромбом?
С
Как рассчитать площадь параллелограмма?
4
1-й способ:
4
60 0
Д
Хватает ли нам данных для решения?
4
А
Н
Из

АВСД – ромб, О – точка пересечения его диагоналей, М – точка пространства, не лежащая в плоскости ромба. Точки А, Д, О лежат в плоскости α.
4. Вычислите площадь ромба, если сторона его равна 4 см, а угол равен 60º. Предложите различные способы вычисления площади ромба.
2-й способ:
А
60 0
4
4
Нужно найти диагонали BD и AC
Из
Д
В
О
А
4
4
АС = 2АО =
30 0
4
ВД = 2ДО =
ДО = 2 (по св-ву прямоугольного
С
Д
О
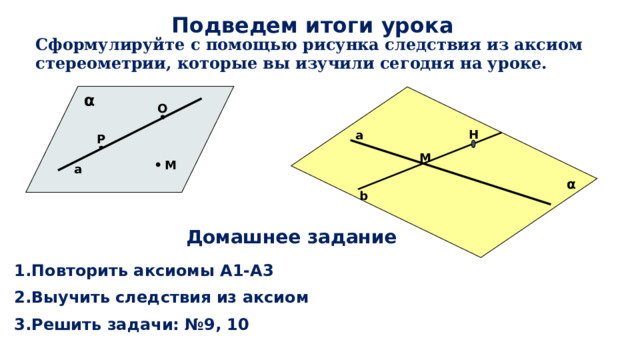
Подведем итоги урока
Сформулируйте с помощью рисунка следствия из аксиом стереометрии, которые вы изучили сегодня на уроке.
α
О
Н
а
Р
М
М
а
α
b
Домашнее задание
- Повторить аксиомы А1-А3
- Выучить следствия из аксиом
- Решить задачи: №9, 10









 все точки b принадлежат плоскости . (по аксиоме А2) 5. Плоскость проходит через а и b и она единственная, т.к. любая плоскость, проходящая через прямые а и b, проходит и через Н, значит α – единственная. Теорема доказана " width="640"
все точки b принадлежат плоскости . (по аксиоме А2) 5. Плоскость проходит через а и b и она единственная, т.к. любая плоскость, проходящая через прямые а и b, проходит и через Н, значит α – единственная. Теорема доказана " width="640"
 С А 2. Две точки каждого отрезка лежат в плоскости, значит все точки каждого из отрезков лежат в плоскости α (по аксиоме А2) Отсюда, отрезки АВ, ВС, АС лежат в плоскости α Ч.т.д. " width="640"
С А 2. Две точки каждого отрезка лежат в плоскости, значит все точки каждого из отрезков лежат в плоскости α (по аксиоме А2) Отсюда, отрезки АВ, ВС, АС лежат в плоскости α Ч.т.д. " width="640"


 С В Докажите самостоятельно, что О D А " width="640"
С В Докажите самостоятельно, что О D А " width="640"















