Презентация на тему " Основы математической логики"

ОСНОВЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ

Учебная презентация по информатике

Автор: Звездина Вера Алексеевна,

учитель информатики

МБОУ «Образовательный центр №1»,

г.Ивантеевка Московской обл.

Определение логики

Ло́гика  (др.-греч. λογική — «здравый смысл, благоразумие; логика», от др.-греч. λόγος — лόгос — «слово; речь; поговорка; логика (здравый смысл)» — наука о законах и приёмах интеллектуальной (мыслительной) познавательной деятельности.

Основная цель логики

Основная цель (функция) логики всегда оставалась неизменной:  исследование того, как из одних утверждений можно выводить другие .

При этом предполагается, что вывод зависит только от способа связи входящих в него утверждений и их строения, а не от их конкретного содержания.

Формы мышления в логике

Понятие - выделяет существенные признаки предмета или класса предметов, отличающие его от других.

Высказывание – повествовательное предложение, выражающее однозначное истинное или ложное суждение об объектах, их свойствах и взаимоотношениях.

Умозаключение - прием мышления, позволяющий на основе одного или нескольких суждений (посылок) получить новое суждение (знание или вывод).

Формы мышления в логике: понятие

В структуре каждого понятия различают две стороны:  содержание и объем.

Содержание понятия составляет совокупность существенных признаков предмета.  

Объем понятия  определяется совокупностью предметов, на которую оно распространяется, и может быть представлено в форме множества объектов, состоящего из элементов множества .

Виды отношений между множествами

Алгебра множеств позволяет исследовать отношения между множествами и, соответственно, объемами понятий. 

Виды отношени й между множествами:

  равнозначность , когда объемы понятий полностью совпадают;

  пересечение , когда объемы понятий частично совпадают;

  подчинение , когда объем одного понятия полностью входит в объем другого и т.д.

Виды отношений между множествами

Для наглядной иллюстрации объемов понятий и соотношений между ними используются диаграммы Эйлера-Венна. Если имеются какие-либо понятия A, B, C и т.д., то объем каждого понятия (множество) можно представить в виде круга, а отношения между этими объемами (множествами) в виде пересекающихся кругов.

Виды отношений между множествами

Рассмотрим их на диаграмме, где

А и В – равнозначные множества,

С пересекается с ними,

а D подчинено им:

Математическая логика

Поскольку новое знание получают посредством разума, логика также определяется как наука о формах и законах мышления - формальная логика .

Математическая логика - область знания, в которой формальная логика изучается математическими методами .

Алгебра логики (Булева алгебра)

Алгебра логики — математический аппарат, развитый и сформулированный в XIX веке английским математиком и логиком Джорджем Булем, с помощью которого записывается, вычисляется, упрощается и преобразуется логическое высказывание. Базовыми элементами, которыми оперирует алгебра логики, являются высказывания .

Виды высказываний

Простые высказывания (иначе называемые логическими переменными ) состоят из одного предложения и обозначаются заглавными буквами латинского алфавита (A, B, C, …).

Сложные высказывания состоят из двух или более простых высказываний, соединенных знаками логических

связок - операций.

Логическое выражение

Если составное высказывание выразить в виде формулы, в которую войдут простые высказывания и знаки логических операций, то получится

логическое выражение ,

значение которого можно вычислить. 

Результатом такого вычисления могут быть только  ложь  (обозначается через 0 ) или  истина (обозначается через 1 ).

Базовые логические операции

Инверсия - унарная операция над суждениями, результатом которой является суждение «противоположное» исходному

Синонимы:  логическое «НЕ», отрицание.

Обозначение : ¬ А или черта

сверху множества.

Базовые логические операции

Конъюнкция   ( А ˄ В или А & B) –

бинарная логическая операция, по смыслу максимально приближенная к союзу «и» . Синонимы:  логическое «И» ,  логическое умножение , иногда просто  «И» .

Базовые логические операции

Дизъюнкция  ( А V В или А | B) -  

бинарная логическая операция, по смыслу максимально приближённая к союзу  «или»  в смысле  «или то, или это, или оба сразу» .

Синонимы: логическое сложение ,  логическое ИЛИ , 

иногда просто  ИЛИ .

Дополнительные логические операции

Импликация  ( А → В) —

бинарная логическая связка, по своему применению приближенная к союзам 

« если …,  то …» .

Синоним: следование

Дополнительные логические операции

Логическая эквиваленция   (A↔B) —логическое выражение, которое является истинным тогда, когда оба простых

логических выражения

имеют одинаковую

истинность.

Исключающее или (A И В)

(сложение по модулю два — XOR) – операция, обратная эквиваленции.

Таблицы истинности

Решение логических выражений принято записывать в виде  таблиц истинности  – таблиц, в которых по действиям показано, какие значения принимает логическое выражение при всех возможных наборах его переменных, и при составлении которых необходимо учитывать  порядок выполнения логических операций.

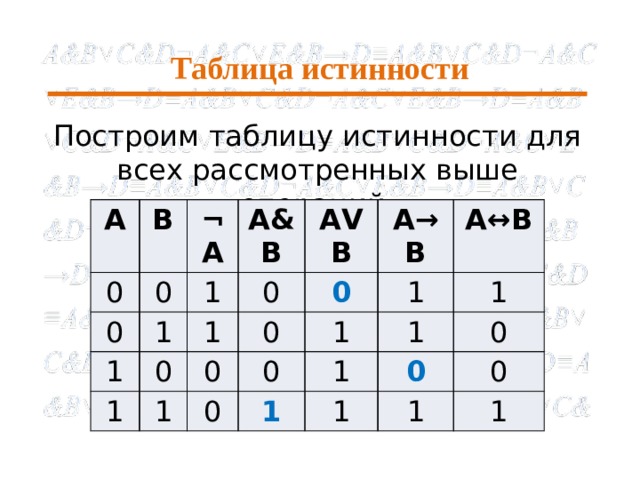
Таблица истинности

Построим таблицу истинности для всех рассмотренных выше операций:

А

В

0

¬ А

0

0

1

А&В

1

1

0

0

АVВ

1

1

1

0

А→В

0

0

0

0

А↔В

1

1

1

1

1

1

0

0

1

1

0

1

Таблица истинности

  Данная таблица построена для всех рассматриваемых нами действий. В ней много правил, но

ВСЕГО ТРИ ИСКЛЮЧЕНИЯ,

выделенных синим цветом:

А & В = 1 , когда все операнды истинны ;

А V В = 0 , когда все операнды ложны ;

А → В = 0 при А = 1 и В = 0 .

Таблица истинности

Поэтому

НЕ НУЖНО ЗАПОМИНАТЬ ПРАВИЛА, ДОСТАТОЧНО ЗАПОМНИТЬ ИСКЛЮЧЕНИЯ И ОПЕРИРОВАТЬ ИМЕННО ИМИ:

А & В = 1 , когда все операнды истинны ;

А V В = 0 , когда все операнды ложны ;

А → В = 0 при А = 1 и В = 0 .

Таблицы истинности

  Порядок выполнения логических операций :

действия в скобках,

¬ инверсия (отрицание),

& (конъюнкция),

V  (дизъюнкция),

→ (импликация),

↔  (эквиваленция).