Презентация на тему: "Пространственная система сил"

1. Пространственная система сходящихся сил.

Пространственную систему сходящихся сил можно заменить одной силой – равнодействующей.

Силовой многоугольник для пространственной системы сил не лежит в одной плоскости, поэтому для определения равнодействующей применяется алгебраический способ (метод проекций).

F Σ = √ F Σ x 2 + F Σ y 2 + F Σ z 2

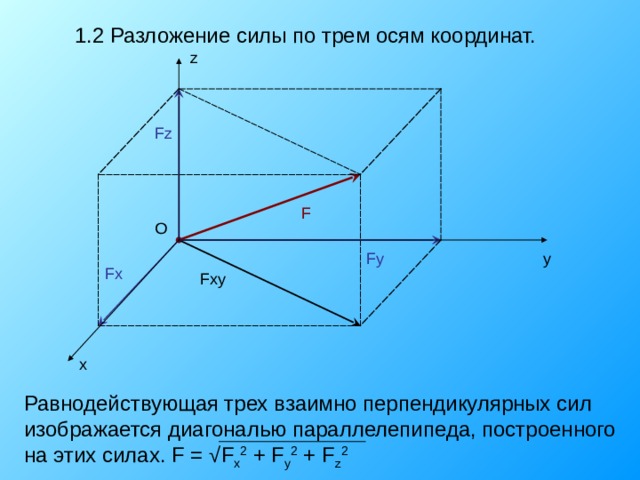
1.2 Разложение силы по трем осям координат.

z

Fz

F

O

Fy

y

Fx

Fxy

x

Равнодействующая трех взаимно перпендикулярных сил изображается диагональю параллелепипеда, построенного на этих силах. F = √ F x 2 + F y 2 + F z 2

1.3 Проекция силы на ось в пространстве.

Правила определения проекции силы остаются прежними.

Если вектор силы параллелен оси , то его проекция равна силе.

Если вектор силы лежит в плоскости, перпендикулярной оси, то его проекция на эту ось равна нулю.

Проекция силы на ось – величина скалярная.

Проекция силы на плоскость – величина векторная.

1.4 Алгебраическое определение равнодействующей пространственной системы сходящихся сил.

F Σ = √ F Σ x 2 + F Σ y 2 + F Σ z 2

1.5 Равновесие пространственной системы сходящихся сил.

Так как пространственную систему сходящихся сил можно заменить только одной силой – равнодействующей, то равновесие будет только в том случае, когда равнодействующая равна нулю. F Σ = 0

Для равновесия ПрССС необходимо, чтобы суммы проекций всех сил системы на оси координат x , y и z равнялись нулю.

Σ F i x = 0

Σ F i y = 0

Σ F i z = 0

уравнения равновесия

ПрССС

2. Момент силы относительно оси.

(xy) Oz

z

F

(xy)

Fxy

О

M z (F) = F xy * h

h

Моментом силы относительно оси называется величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью.

Момент силы относительно оси считается положительным , если при взгляде со стороны положительного направления оси сила стремится вызвать вращение против часовой стрелки.

Момент силы относительно оси равен нулю , если:

• Сила параллельна оси (направлена вдоль оси), так как ее проекция на плоскость, перпендикулярную оси равна нулю.
• Сила пересекает ось, так как при этом плечо равно нулю.

Алгоритм определения момента силы относительно оси.

• Спроецировать силу на плоскость, перпендикулярную оси.
• Найти эту проекцию.
• Определить знак момента
• Найти плечо относительно точки пересечения оси с плоскостью
• Определить момент силы, перемножив проекцию силы на плечо.

3. Равновесие пространственной системы произвольно расположенных сил.

Пространственную систему произвольно расположенных сил можно заменить главным вектором и главным моментом.

Равновесие возможно, если и главный вектор и главный момент этой системы равны нулю.

Σ F i x = 0

Σ F i y = 0

Σ F i z = 0

Σ М x = 0

Σ М y = 0

Σ М z = 0

Для равновесия произвольной пространственной системы сил необходимо, чтобы проекции всех сил на оси x , y , z и моменты всех сил относительно осей x , y и z равнялись нулю.

Уравнения равновесия произвольной пространственной системы сил