Презентация по Астрономии. Тема: "Законы Кеплера"

Законы Кеплера -

Законы движения небесных тел

Законы Кеплера — это три закона движения планет относительно Солнца. Установлены Иоганном Кеплером в начале XVII века как обобщение данных наблюдений Тихо Браге. Причем особенно внимательно Кеплер изучал движение Марса.

• Рассмотрим законы подробнее.

Первый закон Кеплера:

• Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце. Форму эллипса степень его сходства с окружностью будет тогда характеризовать отношение: e=c/a, где с — расстояние от центра эллипса до его фокуса; а — большая полуось. Величина «е» называется эксцентриситетом эллипса. При с=0 и е=0 эллипс превращается в окуржность.

Второй закон Кеплера:

• Каждая планета движется в плоскости, проходящей через центр Солнца, причем площадь сектора орбиты, описанная радиусом-вектором планеты, изменяется пропорционально времени. Применительно к нашей Солнечной системе, с этим законом связаны два понятия: перигелий — ближайшая к Солнцу точка орбиты, и афелий — наиболее удаленная точка орбиты. Тогда можно утверждать, что планета движется вокруг Солнца неравномерно: имея линейную скорость в перигелие больше, чем в афелие.

Третий закон Кеплера:

• Квадраты времен обращения планеты вокруг Солнца относятся как кубы их средних расстояний от Солнца. Этот закон, равно как и первые два, применим не только к движению планет, но и к движению как их естественных, так и искуственных спутников.
• Кеплеровские законы были уточнены и объяснены на основе закона всемирного тяготения Исааком Ньютоном. Закон же всемирного тяготения гласит:  Сила F взаимного притяжения между материальными точками массами m1 и m2, находящиеся на расстоянии r друг от друга, равна: F=Gm1m2/r^2, где G — гравитационная постоянная. Закон открыт Ньютоном также в XVII веке (понятно, что на основе законов Кеплера).

Таким образом в формулировке Ньютона законы Кеплера звучат так:

• — первый закон : под дествием силы тяготения одно небесное тело может двигаться по отношению к другому по окружности, эллипсу, параболе и гиперболе. Надо сказать, что он справедлив для всех тел, между которыми действует взаимное притяжение.  — формулирование второго закона Кеплера не дана, так как в этом не было необходимости.  — третий закон Кеплера сформулирован Ньютоном так: квадраты сидерических периодов планет, умноженные на сумму масс Солнца и планеты, относятся как кубы больших полуосей орбит планет.

Историческая справка законов Кеплера

Астрономия конца XVI века отмечает столкновение двух моделей нашей Солнечной системы: геоцентрическая система Птолемея – где центром вращения всех объектов является Земля, и гелиоцентрическая система Коперника – где Солнце является центральным телом. Модель Солнечной системы К. Птолемея:

И хотя Коперник был ближе к истинной природе Солнечной системы, его работа имела недостатки.

Основным из этих недостатков являлось утверждение, что планеты вращаются вокруг Солнца по круговым орбитам. С учетом этого, модель Коперника практически настолько же не согласовывалась с наблюдениями, как и система Птолемея. Польский астроном стремился исправить данное расхождение при помощи дополнительного движения планеты по кругу, центр которого уже двигался вокруг Солнца — эпицикл. Однако, расхождения в большей своей части не были устранены.

В начале XVII века немецкий астроном Иоганн Кеплер , изучая систему Николая Коперника, а также анализируя результаты астрономических наблюдений датчанина Тихо Браге, вывел основные законы относительно движения планет. Они были названы как Три закона Кеплера.

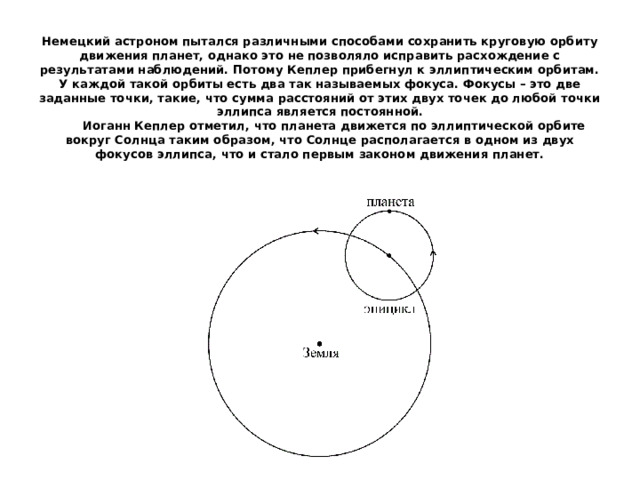
Немецкий астроном пытался различными способами сохранить круговую орбиту движения планет, однако это не позволяло исправить расхождение с результатами наблюдений. Потому Кеплер прибегнул к эллиптическим орбитам. У каждой такой орбиты есть два так называемых фокуса. Фокусы – это две заданные точки, такие, что сумма расстояний от этих двух точек до любой точки эллипса является постоянной. Иоганн Кеплер отметил, что планета движется по эллиптической орбите вокруг Солнца таким образом, что Солнце располагается в одном из двух фокусов эллипса, что и стало первым законом движения планет.

Законы Кеплера:

Проведем радиус-вектор от Солнца, которое располагается в одном из фокусов эллипсоидной орбиты планеты, к самой планете. Тогда за равные промежутки времени данный радиус-вектор описывает равные площади на плоскости, в которой движется планета вокруг Солнца. Данное утверждение является вторым законом.

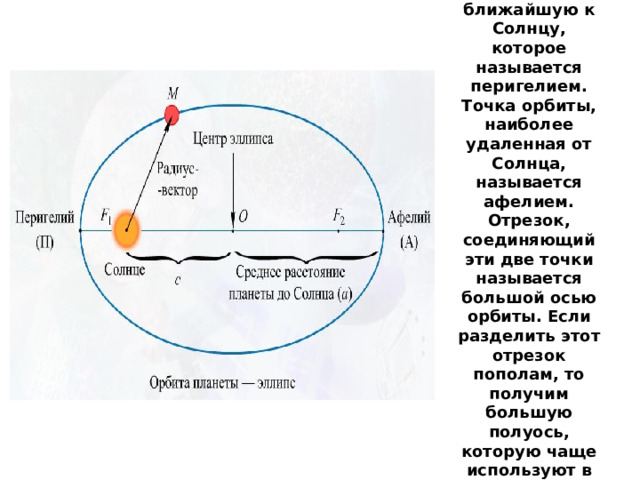
Каждая орбита планеты имеет точку, ближайшую к Солнцу, которое называется перигелием. Точка орбиты, наиболее удаленная от Солнца, называется афелием. Отрезок, соединяющий эти две точки называется большой осью орбиты. Если разделить этот отрезок пополам, то получим большую полуось, которую чаще используют в астрономии.

Третий закон движения планет Кеплера звучит следующим образом: Отношение квадрата периода обращения планеты вокруг Солнца к большой полуоси орбиты этой планеты является постоянным, и также равняется отношению квадрата периода обращения другой планеты вокруг Солнца к большой полуоси этой планеты. Также иногда записывают другое отношение:

Дальнейшее развитие

И хотя законы Кеплера имели относительно невысокую погрешность (не более 1%), все же они были получены эмпирическим способом. Теоретическое же обоснование отсутствовало. Данная проблема позже была решена Исааком Ньютоном, который в 1682-м году открыл закон всемирного тяготения. Благодаря этому закону удалось описать подобное поведение планет. Законы Кеплера стали важнейшим этапом в понимании и описании движения планет.