Презентация по теме: "Цилиндр, конус, шар" по геометрии для учащихся 11 класса.

Тема: «Цилиндр, конус, шар».

Тела вращения

ЦИЛИНДР

Цилиндр



α

Цилиндр – это тело, заключенное между двумя кругами расположенными в параллельных плоскостях и цилиндрической поверхностью.

Цилиндр – это тело, которое описывает прямоугольник при вращении вокруг одной из его сторон.

Верхний и нижний круги – это основания цилиндра.

Прямая проходящая через центры кругов – это ось цилиндра.

Отрезок , который образует поверхность цилиндра, – это образующая цилиндра.

Радиус основания - это радиус цилиндра.

Высота цилиндра - это перпендикуляр между основаниями цилиндра.

Виды цилиндров

Прямой

Наклонный

Сечения цилиндра

Осевое сечение: Плоскость сечения проходит через ось цилиндра.

В сечении –

прямоугольник .

Сечения цилиндра

Сечение плоскостью параллельной оси цилиндра.

В сечении –

прямоугольник.

Сечения цилиндра

Плоскость сечения перпендикулярна оси и параллельна основаниям цилиндра.

В сечении –

круг .

Площадь поверхности цилиндра

h

h

R

2  R

R

КОНУС

Конус

С

α

Конус – это тело, ограниченное конической поверхностью и кругом.

Конус – это тело, которое описывает прямоугольный треугольник при вращении вокруг одного из его катетов.

Круг – это основание конуса.

Точка вне круга с которой соединяются все точки окружности – это вершина конуса.

Прямая проходящая через центр круга и вершину конуса – есть ось конуса.

Отрезок , который образует коническую поверхность– это образующая конуса.

Радиус основания - это радиус конуса.

Высота конуса - это перпендикуляр, опущенный из вершины конуса к основанию.

Сечения конуса

Содержание

Осевое сечение. В сечении –

равнобедренный треугольник.

Сечение плоскостью параллельной основанию конуса. В сечении –

круг.

Площадь поверхности конуса

l

l

2  R

R

R

УСЕЧЁННЫЙ КОНУС

Усеченный конус можно получить вращением прямоугольной трапеции вокруг одной из его боковых сторон.

ШАР, СФЕРА

Шаром называется тело, которое состоит из всех точек пространства, находящихся на одинаковом расстоянии от заданной точки.

Эта точка называется центром шара.

Расстояние от центра шара до любой точки поверхности называется – радиусом шара

Шар можно получить вращением полукруга вокруг оси, содержащей его диаметр.

Сфера – это поверхность все точки которой равноудалены от заданной точки.

Сечения шара

Сечение шара, проходящее через его центр.

В сечении –

круг.

Сечение плоскостью, не проходящей через центр.

В сечении –

круг.

Площадь поверхности шара(сферы)

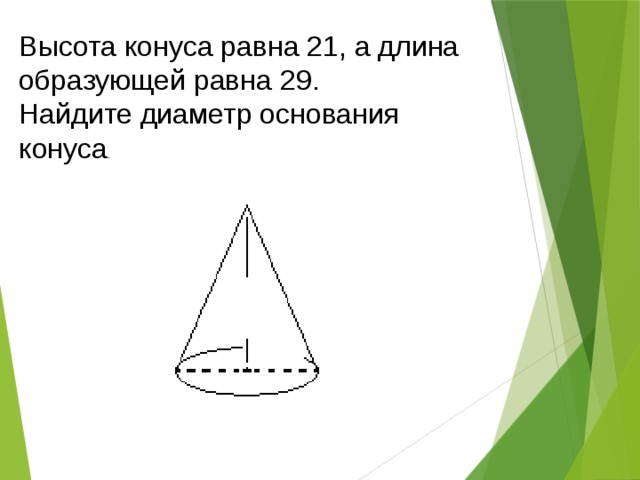
Высота конуса равна 21, а длина образующей равна 29.

Найдите диаметр основания конуса .

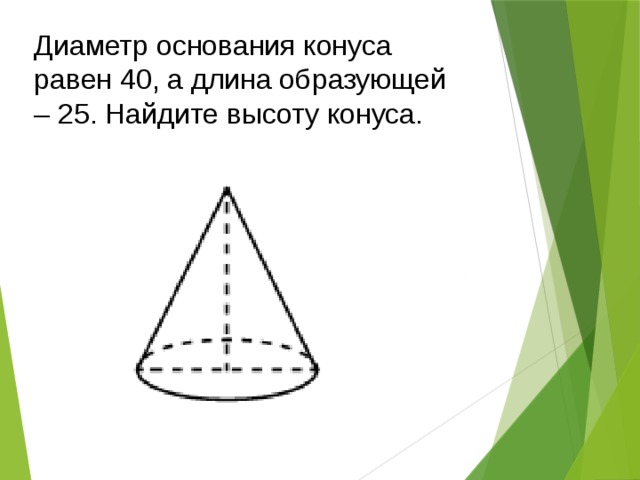
Диаметр основания конуса равен 40, а длина образующей – 25. Найдите высоту конуса.

Площадь боковой поверхности цилиндра равна  12  π , а диаметр основания равен 6. Найдите высоту цилиндра.

Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен  10√2 . Найдите образующую конуса.

Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса.

Образующая конуса равна  80√2 . Найдите радиус сферы.

Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности конуса равна  3√2 . Найдите площадь боковой поверхности цилиндра.

Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна  5√2 . Найдите площадь боковой поверхности конуса.

Шар вписан в цилиндр.   Площадь поверхности шара равна 120. Найдите площадь полной поверхности цилиндра.

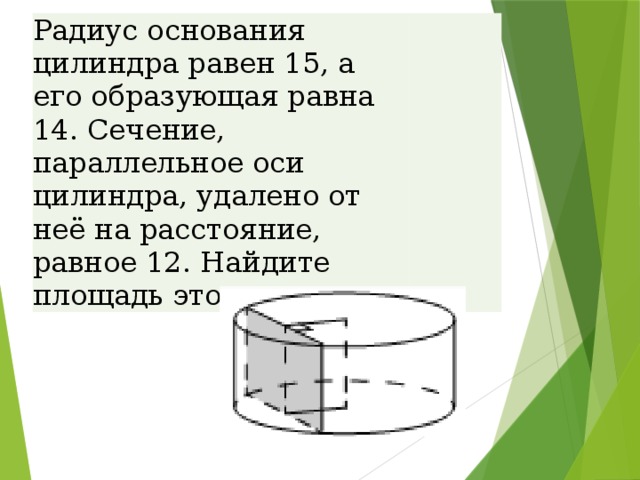
Радиус основания цилиндра равен 15, а его образующая равна 14. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 12. Найдите площадь этого сечения.

Даны два шара с радиусами 6 и 1. Во сколько раз площадь поверхности большего шара больше площади поверхности меньшего?

Даны два конуса. Радиус основания и образующая первого конуса равны соответственно 5 и 6, а второго  —  3 и 4. Во сколько раз площадь боковой поверхности первого конуса больше площади боковой поверхности второго?

Площадь полной поверхности конуса равна 35. Параллельно основанию конуса проведено сечение, делящее высоту в отношении  3:2 , считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.

Радиус основания конуса равен 8, а его высота равна 15. Плоскость сечения содержит вершину конуса и хорду основания, длина которой равна 14. Найдите расстояние от центра основания конуса до плоскости сечения.