Презентация "Подготовка к Публичному зачёту по геометрии 8 класс"

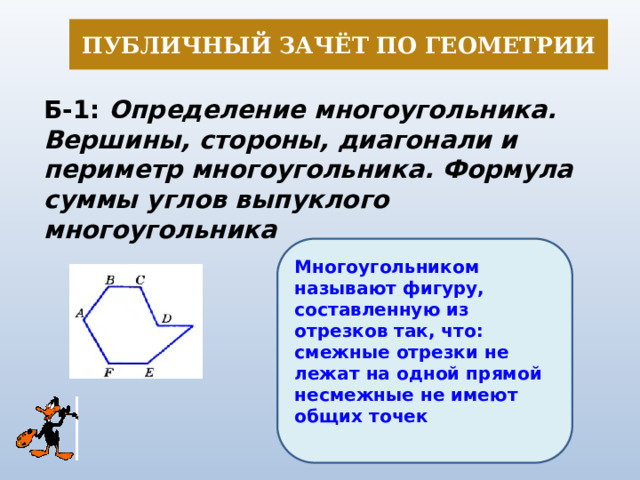
Публичный зачёт по геометрии

Б-1: Определение многоугольника. Вершины, стороны, диагонали и периметр многоугольника. Формула суммы углов выпуклого многоугольника

Многоугольником называют фигуру, составленную из отрезков так, что:

смежные отрезки не лежат на одной прямой

несмежные не имеют общих точек

Публичный зачёт по геометрии

Б-1: Радиус ОВ окружности с центром в точке О пересекает хорду АС в точке D и перпендикулярен ей. Найдите длину хорды АС, если BD= 1 см, а радиус окружности равен 5 см.

ОА=r=5см.(гипотенуза), ОD=5-1=4см.(катет). По т. Пифагора AD 2 =5 2 -4 2 =3

АС=3⸱2=6см. Ответ:6см.

Публичный зачёт по геометрии

Б-2: Определение и свойства параллелограмма

Параллелограмм – это четырехугольник, у которого противоположные стороны попарно – параллельны.

1° В параллелограмме противоположные углы равны. В параллелограмме противоположные стороны равны.

2° Диагонали параллелограмма точкой пересечения делится пополам.

3° В параллелограмме сумма углов прилежащих к одной стороне равна 180°.

Публичный зачёт по геометрии

Б-2:Проектор пол­но­стью освещает экран  А  вы­со­той 80 см, рас­по­ло­жен­ный на рас­сто­я­нии 250 см от проектора. На каком наи­мень­шем расстоянии (в сантиметрах) от про­ек­то­ра нужно рас­по­ло­жить экран  б  вы­со­той 160 см, чтобы он был пол­но­стью освещён, если на­строй­ки проектора оста­ют­ся неизменными?

Составляем пропорцию:

х/250 = 160/80

Х=160*250/80

Ответ:500см.

Публичный зачёт по геометрии

Б-3: Определение и свойства прямоугольника

Прямоугольник - параллелограмм у которого все углы прямые.

Свойства прямоугольника:

1° В прямоугольнике противоположные стороны равны.

2° В прямоугольнике диагонали точкой пересечения делится пополам.

3° В прямоугольнике диагонали равны.

Публичный зачёт по геометрии

Б-3: Найдите ве­ли­чи­ну (в градусах) впи­сан­но­го угла  α , опи­ра­ю­ще­го­ся на хорду   AB , рав­ную ра­ди­у­су окружности.

Треугольник АОВ равносторонний, значит ∠АОВ=60 ° , а он центральный . ∠АСВ=60:2=30 °, так как он вписанный и опирается на ту же дугу АВ.

Ответ: 30 °

.

Публичный зачёт по геометрии

Б-4: Определение и свойства ромба

Ромб – это параллелограмм, у которого все стороны равны.

Свойства ромба:

1° В ромбе противоположные углы равны.

2° Диагонали в ромбе точкой пересечения делится пополам.

3° Диагонали ромба перпендикулярны и являются биссектрисами его углов.

Публичный зачёт по геометрии

Б-4: Два па­ро­хо­да вышли из порта, сле­дуя один на север, дру­гой на запад. Ско­ро­сти их равны со­от­вет­ствен­но 15 км/ч и 20 км/ч. Какое рас­сто­я­ние (в километрах) будет между ними через 2 часа?

Найдем расстояние, ко­то­рое прошёл пер­вый теплоход: 15 ⸱2=30км/ч

Найдем расстояние, ко­то­рое прошёл вто­рой теплоход: 20 ⸱2=40км/ч

Теплоходы дви­жут­ся вдоль ка­те­тов пря­мо­уголь­но­го треугольника, ги­по­те­ну­за ко­то­ро­го яв­ля­ет­ся рас­сто­я­ни­ем между ними. Най­дем это рас­сто­я­ние по тео­ре­ме Пифагора:  с 2 =30 2 +40 2 с 2 =2500 с=50

  Ответ: 50.

Публичный зачёт по геометрии

Б-6: Один из острых углов прямоугольного треугольника 37°. Найти второй острый угол.

Угол Е = 90 °, так как треугольник Е FD прямоугольный, а

∠ Е+ ∠ F + ∠ D =180° , значит ∠ F =180-90-37= 53°

F

0

37

Е

D

O

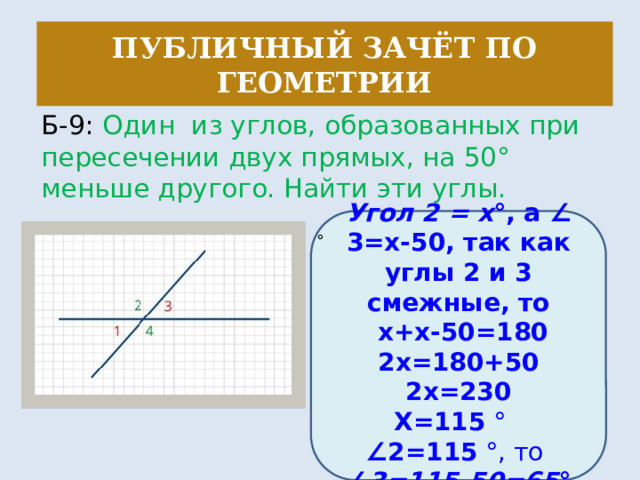
Публичный зачёт по геометрии

Б-9: Один из углов, образованных при пересечении двух прямых, на 50° меньше другого. Найти эти углы.

Угол 2 = х °, а ∠ 3=х-50, так как углы 2 и 3 смежные, то

х+х-50=180

2х=180+50

2х=230

Х=115 °

∠ 2=115 °, то ∠ 3=115-50=65 °

°

Публичный зачёт по геометрии

Б-3: Определение и свойство смежных углов (формулировка)

Смежными называются два угла, у которых одна сторона общая, а другие стороны являются продолжениями друг друга.

Сумма смежных углов равна 180°

С

А

D

В

Публичный зачёт по геометрии

Б-4: Определение и свойство вертикальных углов (формулировка).

Вертикальными  углами называются два угла, у которых стороны одного угла являются продолжениями сторон другого угла.

Вертикальные углы равны.

11

Публичный зачёт по геометрии

Б-6: Определение треугольника. Стороны, вершины, углы треугольника. Периметр треугольника.

Треугольник - это геометрическая фигура, состоящая из трех точек, которые не лежат на одной прямой, и трех отрезков, последовательно соединяющих эти точки. Указанные точки называются вершинами треугольника, а отрезки - сторонами.

Периметр треугольника – это сумма длин всех его сторон.

А

С

13

Публичный зачёт по геометрии

Б-7: Определение равнобедренного треугольника. Равносторонний треугольник. Сформулировать свойства равнобедренного треугольника.

У равнобедренного треугольника углы при основании равны . 

13