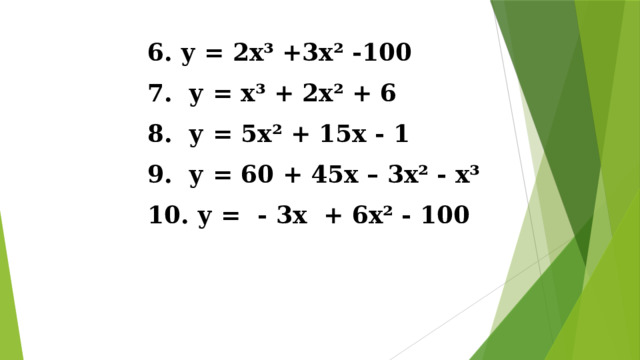Россия, Орск
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Был в сети 06.05.2024 14:31
Жаппасбаев Аманкос Сагинтаевич
учитель
49 лет
986
50 089 
Местоположение
Специализация
Презентация "Применение производной при исследовании функции"
Категория:
Математика
16.04.2024 04:06
Просмотр содержимого документа
«Презентация "Применение производной при исследовании функции"»
ПРИМЕНЕНИЕ
ПРОИЗВОДНОЙ
к исследованию функции и построению графика функции
Жаппасбаев А.С.
10 класс
Для определения промежутков возрастания и убывания функции можно использовать и производную .
0 , то f(x) – возрастает б) если f´(x) , то f(x) – убывает в) если f´(x) = 0 , то f(x) – постоянна (константа) " width="640"
Теорема :
Если f(x) – непрерывна на промежутке и имеет f´(x), то
а) если f´(x) 0 , то f(x) – возрастает
б) если f´(x) , то f(x) – убывает
в) если f´(x) = 0 , то f(x) – постоянна
(константа)
0 , то f(x) – возрастает б) если f´(x) , то f(x) – убывает в) если f´(x) = 0 , то f(x) – постоянна (константа) " width="640"
Теорема :
Если f(x) – непрерывна на промежутке и имеет f´(x), то
а) если f´(x) 0 , то f(x) – возрастает
б) если f´(x) , то f(x) – убывает
в) если f´(x) = 0 , то f(x) – постоянна
(константа)
0 , при x ϵ (-∞; 1) и (3; + ∞) f ´(x) , при х ϵ (1; 3) Ответ: при x ϵ (-∞; 1) и (3; + ∞) функция возрастает, а при х ϵ (1; 3) - убывает - + f ´(x) + х 1 3 f(x) " width="640"
Например : найти промежутки монотонности функции f(x) = x³ - 6x² + 9x – 1
1) f´(x) = 3x² - 12x + 9
2) Найдем стационарные точки:
f´(x) = 0, 3x² - 12x + 9 = 0
x² - 4x + 3 = 0
x = 1 и х = 3
3)
4)
5) f ´(x) 0 , при x ϵ (-∞; 1) и (3; + ∞)
f ´(x) , при х ϵ (1; 3)
Ответ: при x ϵ (-∞; 1) и (3; + ∞) функция возрастает, а при х ϵ (1; 3) - убывает
-
+
f ´(x)
+
х
1
3
f(x)
Нахождение
точек экстремума
функции
Определения
- Точка х о называется точкой минимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой выполняется неравенство
f(х) ≥ f(х о )
- Точка х о называется точкой максимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой выполняется неравенство
f(х) ≤ f(х о )
х0 - неравенство f΄(х) 0, то х0 – точка минимума функции у = f(х) х 0 - min " width="640"
Теорема
Пусть функция у = f(х) непрерывна на промежутке Х и имеет внутри промежутка стационарную или критическую точку х=х0. Тогда:
а) если у этой точки существует такая окрестность, в которой при х х0 выполняется неравенство f΄(х) х х0 - неравенство f΄(х) 0, то
х0 – точка минимума функции у = f(х)
х 0
- min
х0 - неравенство f΄(х) 0, то х0 – точка минимума функции у = f(х) х 0 - min " width="640"
Теорема
Пусть функция у = f(х) непрерывна на промежутке Х и имеет внутри промежутка стационарную или критическую точку х=х0. Тогда:
а) если у этой точки существует такая окрестность, в которой при х х0 выполняется неравенство f΄(х) х х0 - неравенство f΄(х) 0, то
х0 – точка минимума функции у = f(х)
х 0
- min
Найдите точки экстремума функции и определите их характер
- у = 7 + 12х - х²
- у = 3х³ + 2х² - 7
- у = -2х³ + 21х² + 19
- у = 3х² - х³
- у = х + 4/х
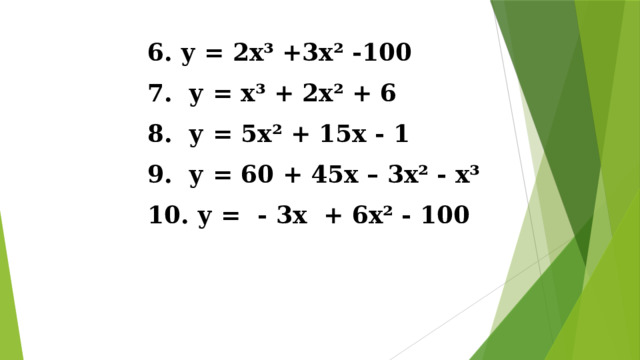
6. у = 2х³ +3х ² -100
7. у = х³ + 2х² + 6
8. у = 5х² + 15х - 1
9. у = 60 + 45х – 3х² - х³
10. у = - 3х + 6х² - 100
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
