Презентация "Тригонометрическая и показательная форма комплексного числа"

Тригонометрическая и показательная форма комплексного числа

Преподаватель СП ГБПОУ ОМЛ

Н.М. Зудина

определение

Любое комплексное число (кроме нуля) z = a + bi можно записать в тригонометрической форме:

z = |z|· (cos ϕ + i·sin ϕ ) ,

где |z| - это модуль комплексного числа ,

а ϕ – аргумент комплексного числа

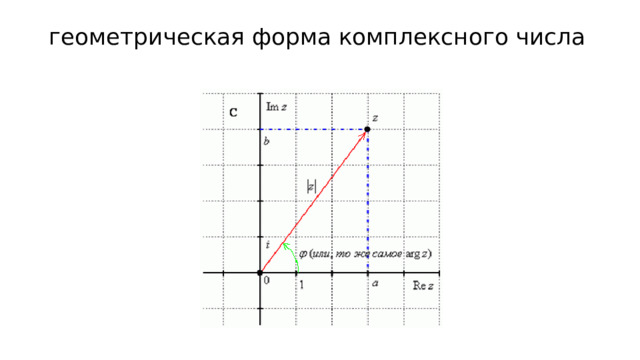
геометрическая форма комплексного числа

определение

Модулем комплексного числа z называется расстояние от начала координат до соответствующей точки комплексной плоскости

( модуль – это длина радиус-вектора):

| z | или r.

|z| =

определение

Аргументом комплексного числа z называется угол ϕ между положительной полуосью действительной оси и радиус вектором, проведённым из начала координат к соответствующей точке. (аргумент не определён для единственного числа z = 0). Обозначают ϕ или arg z

arg z = arctg

!!! Данная формула работает только в правой полуплоскости (1 и 4 четверти)

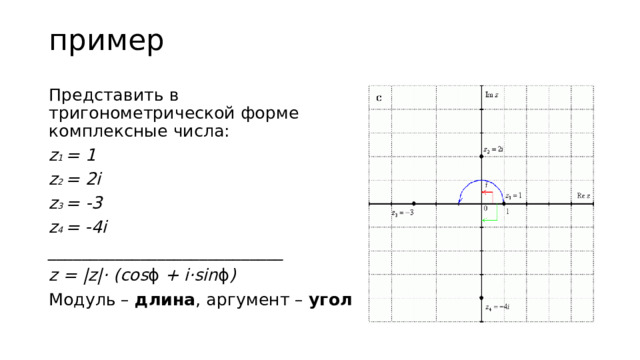
пример

Представить в тригонометрической форме комплексные числа:

z 1 = 1

z 2 = 2i

z 3 = -3

z 4 = -4i

____________________________

z = |z|· (cos ϕ + i·sin ϕ )

Модуль – длина , аргумент – угол

0 (1-я и 4-я координатные четверти, или правая полуплоскость), то аргумент нужно находить по формуле   arg z = arctg 2) Если a 0 (2-я координатная четверть), то аргумент нужно находить по формуле arg z = π + arctg 3) Если a arg z = - π + arctg " width="640"

Формулы для нахождения аргумента:

1) Если a 0 (1-я и 4-я координатные четверти, или правая полуплоскость), то аргумент нужно находить по формуле

arg z = arctg

2) Если a 0 (2-я координатная четверть), то аргумент нужно находить по формуле

arg z = π + arctg

3) Если a

arg z = - π + arctg

пример

Представить в тригонометрической форме комплексные числа:

z 1 = 3 + i

z 2 = - 2 + 4i

z 3 = - 2 – 2i

z 4 = 1 - i

определение

Любое комплексное число (кроме нуля) z = a + bi можно записать в показательной форме:

z = |z|· ,

где |z| - это модуль комплексного числа,

а ϕ – аргумент комплексного числа

Возведение комплексных чисел в степень

Формула Муавра

= · (cos(n ϕ) + i·sin(n ϕ) )

Пример: дано комплексное число z 1 = 3 + i.

Найти .