Россия, Находка
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 25.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 21.05.2025 15:48
Коптева Лайсан Мунавировна
учитель математики
61 год
848 920
11 
Местоположение
Специализация
Презентация "Задачи на теорию чисел", задание № 19 ЕГЭ по математике, профильный уровень
Категория:
Математика
26.07.2024 12:34
Просмотр содержимого документа
«Презентация "Задачи на теорию чисел", задание № 19 ЕГЭ по математике, профильный уровень»
Задача №19 ЕГЭ
Задачи на теорию чисел
Алгоритм решения задания №19 (числа и их свойства)
1. Анализ условия задачи .
2. Выделение ключевых моментов .
3. Применение теоретических знаний .
4. Решение уравнений/неравенств .
5. Логический анализ .
6. Проверка ответа .
Критерии оценивания
A = 3k (9n + 6) 3 = (n + 1) 3. = (10n + 7) 3 . 10n + 7 = 9n + n + 6 + 1 = (9n + 6) + (n + 1); Выпишем несколько чисел n , таких, что (n + 1) 3 , и найдём, чему будут равны k и A . n k 2 A 9 5 19 27 8 11 29 57 39 87 14 117 49 147 231 = 3 · 77 = 3 · (9 + 19 + 49) = 27 + 57 + 147 . " width="640"
ЕГЭ 2020 №18.1
На доске написано несколько различных натуральных чисел, каждое из которых делится на 3 и оканчивается на 7.
а) Может ли сумма этих чисел быть равна 231?
б) Может ли сумма этих чисел быть равна 1590?
в) Какое наибольшее количество чисел может быть на доске, если их сумма равна 1056?
На доске написано несколько различных натуральных чисел, каждое из которых делится на 3 и оканчивается на 7.
а) Может ли сумма этих чисел быть равна 231?
Решение. а) Да, может. 27 + 57 + 147 = 231 .
Как мы получили пример?
Числа A, которые делятся на 3 и оканчиваются на 7 можно представить как
или A = 10n + 7, где kN и nN =
A = 3k
(9n + 6) 3 = (n + 1) 3.
= (10n + 7) 3 . 10n + 7 = 9n + n + 6 + 1 = (9n + 6) + (n + 1);
Выпишем несколько чисел n , таких, что (n + 1) 3 , и найдём, чему будут равны k и A .
n
k
2
A
9
5
19
27
8
11
29
57
39
87
14
117
49
147
231 = 3 · 77 = 3 · (9 + 19 + 49) = 27 + 57 + 147 .
1590 . Противоречие. Следовательно, требуемое невозможно . " width="640"
ЕГЭ 2020 №19.1
На доске написано несколько различных натуральных чисел, каждое из которых делится на 3 и оканчивается на 7.
а) Может ли сумма этих чисел быть равна 231?
б) Может ли сумма этих чисел быть равна 1590?
в) Какое наибольшее количество чисел может быть на доске, если их сумма равна 1056?
б) Предположим, что это возможно.
Решение.
Каждое число оканчивается на 7 , а их сумма на 0 .
Такое возможно, если количество чисел кратно 10 .
Значит, таких чисел в любом случае не меньше 10 .
Число, делящееся на 3 , оканчивается на 7 только, если оно имеет вид 3n , где n N и
n оканчивается на 9 .
Найдём сумму 10 наименьших чисел, оканчивающихся на 7 и кратных 3 :
27 + 57 + 87 + … = 3 · (9 + 19 + … + 99) = 3 · 540 = 1620 1590 . Противоречие.
Следовательно, требуемое невозможно .
ЕГЭ 2020 №19.1
На доске написано несколько различных натуральных чисел, каждое из которых делится на 3 и оканчивается на 7.
а) Может ли сумма этих чисел быть равна 231?
б) Может ли сумма этих чисел быть равна 1590?
в) Какое наибольшее количество чисел может быть на доске, если их сумма равна 1056?
Решение. в) Чтобы узнать последнюю цифру в сумме из n чисел, оканчивающихся на 7 ,
нужно определить последнюю цифру в числе 7 n .
Последняя цифра равна 6 , если n = 8 , 18, … и т.д.
Пример . Найдём сумму 8 наименьших чисел , оканчивающихся на 7 :
27 + 57 + 87 + …+ 237 = 3 · (9 + 19 + … + 79) = 3 · 88 · 4 = 1056.
Таким образом, наибольшее количество чисел на доске равно 8 .
Ответ : а) да; б) нет; в) 8.
Замечания
В пункте в) рассуждения, приводящие к тому, что количество чисел обязано оканчиваться на 8, т.е. n = 8, 18, … и т.д., называются оценкой .
Однако одной лишь оценки не достаточно для получения 1 балла , ведь
в реальности пример , реализующий эту оценку, может и не существовать .
В данной задаче построение (единственного!) примера, реализующего эту оценку, т.е. 27, 57, …, 237, оценка + пример даёт 2 балла в пункте в .
Структура задания 18:
а) Да + пример; нет + доказательство;
б) Нет + доказательство;
в) Оценка + пример.
140? б) Может ли быть верным уравнение A = B · C, если 440 ⩽ A 500? в) Найдите наибольшее число A до 900, для которого выполняется A = B · C. Решение. а) Да, может. Например, если A = 625 , B = 25 , C = 25 , то получаем равенство: 625 = 25 · 25 . Или, например, если A = 150 , B = 15 , C = 10 , то получаем равенство: 150 = 15 · 10 . " width="640"
№ 19.2 ЕГЭ 2023 (основная волна)
На доске написано трёхзначное число A . Серёжа зачёркивает одну цифру и получает двузначное число B , затем Коля записывает число A и зачеркивает одну цифру (возможно ту же, что Серёжа) и получает число C . а) Может ли быть верным уравнение A = B · C, если A 140? б) Может ли быть верным уравнение A = B · C, если 440 ⩽ A 500? в) Найдите наибольшее число A до 900, для которого выполняется A = B · C.
Решение. а) Да, может. Например, если A = 625 , B = 25 , C = 25 ,
то получаем равенство: 625 = 25 · 25 .
Или, например, если A = 150 , B = 15 , C = 10 ,
то получаем равенство: 150 = 15 · 10 .
140? б) Может ли быть верным уравнение A = B · C, если 440 ⩽ A 500? в) Найдите наибольшее число A до 900, для которого выполняется A = B · C. Решение. б) Если 440 ⩽ A , то первая цифра числа A равна 4 . Тогда вторая цифра числа A не меньше 4 . Тогда B ⩾ 40 и C ⩾ 40 . Значит, A = B · C ⩾ 40 · 40 = 1600 500 . Тогда указанное равенство A = B · C не может быть верным . " width="640"
№ 19.2 ЕГЭ 2023 (основная волна)
На доске написано трёхзначное число A . Серёжа зачёркивает одну цифру и получает двузначное число B , затем Коля записывает число A и зачеркивает одну цифру (возможно ту же, что Серёжа) и получает число C . а) Может ли быть верным уравнение A = B · C, если A 140? б) Может ли быть верным уравнение A = B · C, если 440 ⩽ A 500? в) Найдите наибольшее число A до 900, для которого выполняется A = B · C.
Решение. б) Если 440 ⩽ A , то первая цифра числа A равна 4 .
Тогда вторая цифра числа A не меньше 4 . Тогда B ⩾ 40 и C ⩾ 40 .
Значит, A = B · C ⩾ 40 · 40 = 1600 500 .
Тогда указанное равенство A = B · C не может быть верным .
№ 19.2 ЕГЭ 2023 (основная волна)
На доске написано трёхзначное число A . Серёжа зачёркивает одну цифру и получает двузначное число B , затем Коля записывает число A и зачеркивает одну цифру (возможно ту же, что Серёжа) и получает число C . в) Найдите наибольшее число A до 900, для которого выполняется A = B · C.
Решение в) Сначала приведем пример: A = 810 , B = 81 , C = 10 , тогда
B · C = 81 · 10 = 810 = A.
Пусть A = . Тогда заметим, что если оба мальчика зачеркнули b или c ,
то B · C ⩾ 6400 . Такое не подходит .
Значит, один из мальчиков вычеркнул первую цифру, пусть это был Серёжа.
Если b = 0 , то B = c . Тогда B · C ⩽ · ⩽ 9 · 89 = 801 .
B · C не удовлетворяет условию.
А B · C , При с = 1 A = 81181 · 11 = А B · C , при с = 7 A = 817 81 · 17 = А B · C , при с = 2 A = 812 81 · 12 = А B · C , при с = 3 A = 813 81 · 13 = А B · C , при с = 8 A = 818 81 · 18 = А B · C , при с = 4 A = 814 81 · 14 = А B · C , при с = 9 A = 819 81 · 19 = А B · C , Тогда c может равняться только 0 . Получили наш пример: A = 810 , B = 81 , C = 10 . при с = 5 A = 815 81 · 15 = А B · C , " width="640"
№ 19.2 ЕГЭ 2023 (основная волна)
На доске написано трёхзначное число A . Серёжа зачёркивает одну цифру и получает двузначное число B , затем Коля записывает число A и зачеркивает одну цифру (возможно ту же, что Серёжа) и получает число C . в) Найдите наибольшее число A до 900, для которого выполняется A = B · C.
Решение в) Тогда b ⩾ 1 , значит, B = = 10b + c .
Оценим B · 80 . B · 80 = (10b + c) · 80 = 800b + 80c ⩾ 800. При b ⩾ 2 B · 80 ⩾ 1600 .
Тогда если Коля не вычеркнул первую цифру , то b = 1 . Значит, A = .
при с = 6 A = 81681 · 16 = А B · C ,
При с = 1 A = 81181 · 11 = А B · C ,
при с = 7 A = 817 81 · 17 = А B · C ,
при с = 2 A = 812 81 · 12 = А B · C ,
при с = 3 A = 813 81 · 13 = А B · C ,
при с = 8 A = 818 81 · 18 = А B · C ,
при с = 4 A = 814 81 · 14 = А B · C ,
при с = 9 A = 819 81 · 19 = А B · C ,
Тогда c может равняться только 0 .
Получили наш пример: A = 810 , B = 81 , C = 10 .
при с = 5 A = 815 81 · 15 = А B · C ,
810 . Тогда B 28 , так как = 784 . Значит, B = 29 . Но тогда A = 841 , что невозможно , так как 841 не оканчивается на 29 . Таким образом, 810 — наибольшее возможное A . Ответ: а) Да, может; б) Нет, не может; в) 810. " width="640"
№ 19.2 ЕГЭ 2023 (основная волна)
На доске написано трёхзначное число A . Серёжа зачёркивает одну цифру и получает двузначное число B , затем Коля записывает число A и зачеркивает одну цифру (возможно ту же, что Серёжа) и получает число C . в) Найдите наибольшее число A до 900, для которого выполняется A = B · C.
Пусть оба мальчика вычеркнули первую цифру . Тогда B = C = .
Решение в)
Значит, A = . Если A , то B . Нам надо найти A 810 .
Тогда B 28 , так как = 784 . Значит, B = 29 .
Но тогда A = 841 , что невозможно , так как 841 не оканчивается на 29 .
Таким образом, 810 — наибольшее возможное A .
Ответ: а) Да, может; б) Нет, не может; в) 810.
№ 19.3 ЕГЭ 2023
Есть числа A и B. Из них можно сделать числа A + 2 и B − 1 или B + 2 и A − 1, только если следующая пара этих чисел будет натуральной. Известно, что A = 7, B = 11.
а) Можно ли за 20 ходов создать пару, где одно из чисел равно 50?
б) За сколько ходов можно сделать пару, где сумма чисел будет равна 600?
в) Какое наибольшее число ходов можно сделать, чтобы оба числа не превышали 50?
Решение. а) При каждом действии сумма чисел увеличивается ровно на 1 .
Действительно:
• Если было (A, B) , и стало (A + 2, B − 1) , то сумма A + B стала A + 2 + B − 1 = A + B + 1.
• Если было (A, B) , и стало (A − 1, B + 2) , то сумма A + B стала A − 1 + B + 2 = A + B + 1.
Значит, за 20 ходов сумма увеличится на 20 , то есть будет равна 7 + 11 + 20 = 38 .
Нельзя представить 38 в виде суммы двух натуральных слагаемых, одно из которых 50 .
№ 19.3 ЕГЭ 2023
Есть числа A и B. Из них можно сделать числа A+ 2 и B −1 или B + 2 и A−1, только если следующая пара этих чисел будет натуральной. Известно, что A = 7, B = 11.
б) За сколько ходов можно сделать пару, где сумма чисел будет равна 600?
в) Какое наибольшее число ходов можно сделать, чтобы оба числа не превышали 50?
Решение.
б) Как было показано в пункте а),
сумма чисел увеличивается на 1 после каждого хода.
Начальная сумма чисел равна A + B = 7 + 11 = 18 .
Тогда понадобится ровно 600 − 18 = 582 хода для достижения искомой суммы,
которую можно получить путём проведения следующего алгоритма 291 раз :
(A, B) → (A + 2, B - 1) → (A + 1, B + 1).
№ 19.3 ЕГЭ 2023
Есть числа A и B. Из них можно сделать числа A+ 2 и B − 1 или B + 2 и A−1, только если следующая пара этих чисел будет натуральной. Известно, что A = 7, B = 11.
в) Какое наибольшее число ходов можно сделать, чтобы оба числа не превышали 50?
Решение. в) Рассмотрим разность вида «второе число — первое число» .
Вначале она равна B − A . Далее возможны два варианта :
B + 2 − ( A − 1 ) = B − A + 3 либо B − 1 − ( A + 2 ) = B − A − 3 .
Числа B − A , B − A + 3 и B − A − 3 имеют одинаковый остаток при делении на три .
То есть разность второго и первого чисел (именно в этом порядке)
всегда даёт один и тот же остаток при делении на 3.
Вначале эта разность равна 11 − 7 = 4 даёт остаток 1 при делении на 3 .
№ 19.3 ЕГЭ 2023
Есть числа A и B. Из них можно сделать числа A+ 2 и B −1 или B + 2 и A−1, только если следующая пара этих чисел будет натуральной. Известно, что A = 7, B = 11.
в) Какое наибольшее число ходов можно сделать, чтобы оба числа не превышали 50?
Решение. в)
По условию оба числа не превышают 50 , то максимальное количество ходов
возможно при максимальной сумме чисел, которая равна 100 .
Каждый ход меняет разность пары на 3 .
Начальная разность чисел равнялась 11 − 7 = 4 .
Тогда новая пара чисел не сможет в разности дать нулевой остаток при делении на 3 ,
то есть A ≠ B . Тогда максимальная сумма чисел указанных чисел уже не 100 , а 99 .
Из чисел (7, 11) сделаем пару чисел (49, 50) за 99 −18 = 81 ход следующим образом :
(A, B) → (A + 2, B - 1) → (A + 1, B + 1).
(7, 11) (46, 50)
→ (48, 49) → (50, 48) → (49, 50) .
Ответ: а) Нет, нельзя; б) 582; в) 81.
№ 19.4 ЕГЭ-2016
Трёхзначное натуральное число, в десятичной записи которого нет нулей, разделили на произведение его цифр.
а) Может ли получившееся частное быть равным 5?
б) Может ли получившееся частное быть равным 1?
в) Какое наименьшее значение может принимать это частное?
Решение. а) Пусть наше трехзначное число 100a + 10b + c . = 5.
Заметим, все цифры числа не равны нулю и число кратно 5 , тогда c = 5 .
100a + 10b + 5 = 25ab, 20a + 2b + 1 = 5ab.
Пусть a = 1 , тогда 20 + 2b + 1 = 5a ,
21 = 3b , b = 7 .
Итак , = 5 .
0) , что невозможно . Указанное в условии частное не может быть равно 1 . " width="640"
№ 19.4 ЕГЭ-2016
Трёхзначное натуральное число, в десятичной записи которого нет нулей, разделили на произведение его цифр.
б) Может ли получившееся частное быть равным 1?
в) Какое наименьшее значение может принимать это частное?
Решение . б) Пусть наше трехзначное число 100a + 10b + c = abc .
Тогда 10b + c = a ( bc 100 ) ,
Правая часть отрицательна ( bc 100 , а левая положительна ( 10b + с 0) ,
что невозможно .
Указанное в условии частное не может быть равно 1 .
№ 19.4 ЕГЭ-2016
Трёхзначное натуральное число, в десятичной записи которого нет нулей, разделили на произведение его цифр.
б) Может ли получившееся частное быть равным 1?
в) Какое наименьшее значение может принимать это частное?
Решение. в) Частное числа и произведения его цифр равно
= + + + + = .
Итак , а = b = с = 9 .
.
Ответ: а) да; б) нет; в) .
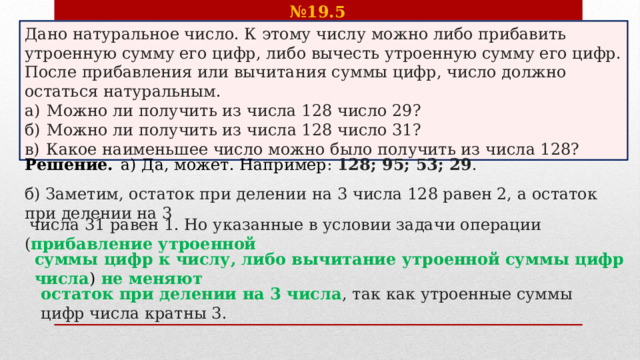
№ 19.5
Дано натуральное число. К этому числу можно либо прибавить утроенную сумму его цифр, либо вычесть утроенную сумму его цифр. После прибавления или вычитания суммы цифр, число должно остаться натуральным.
а) Можно ли получить из числа 128 число 29?
б) Можно ли получить из числа 128 число 31?
в) Какое наименьшее число можно было получить из числа 128?
Решение. а) Да, может. Например : 128; 95; 53; 29 .
б) Заметим, остаток при делении на 3 числа 128 равен 2, а остаток при делении на 3
числа 31 равен 1. Но указанные в условии задачи операции ( прибавление утроенной
суммы цифр к числу, либо вычитание утроенной суммы цифр числа ) не меняют
остаток при делении на 3 числа , так как утроенные суммы цифр числа кратны 3.
№ 19.5
Дано натуральное число. К этому числу можно либо прибавить утроенную сумму его цифр, либо вычесть утроенную сумму его цифр. После прибавления или вычитания суммы цифр, число должно остаться натуральным.
в) Какое наименьшее число можно было получить из числа 128?
Решение. в) По замеченному в пункте б, понимаем, что наименьшим числом не может
оказаться 1, так как числа 128 и 1 имеют разные остатки при делении на 3 .
Попробуем подобрать пример для 2.
95 53 77 35 59 17 41 26 2 .
или
95 53 29 62 38 5 20 26 2 .
Ответ : а) да; б) нет; в) 2.
№ 19.6
Дана правильная несократимая дробь , где и натуральные числа.
За один ход можно увеличить числитель на знаменатель, а знаменатель — на два числителя, то есть получить дробь .
а) Можно ли из дроби получить дробь ?
б) Можно ли из некоторой дроби за 3 хода получить дробь, равную ?
в) Дробь меньше . Найдите ее наибольшее значение, которое нельзя получить из другой правильной несократимой дроби за 2 хода.
Решение . а) Да, можно:
№ 19.6
Дана правильная несократимая дробь , где и натуральные числа.
За один ход можно увеличить числитель на знаменатель, а знаменатель — на два числителя, то есть получить дробь .
б) Можно ли из некоторой дроби за 3 хода получить дробь, равную ?
в) Дробь меньше . Найдите ее наибольшее значение, которое нельзя получить из другой правильной несократимой дроби за 2 хода.
Решение . б) Если начальная дробь , то через три хода
Несократимая дробь остается несократимой , так как по алгоритму Евклида
НОД( ; ) = НОД( ; ) = НОД( ; ) = .
НОД (a, b) = НОД (b, с), где с — остаток от деления a на b .
№ 19.6
Дана правильная несократимая дробь , где и натуральные числа.
За один ход можно увеличить числитель на знаменатель, а знаменатель — на два числителя, то есть получить дробь .
б) Можно ли из некоторой дроби за 3 хода получить дробь, равную ?
в) Дробь меньше . Найдите ее наибольшее значение, которое нельзя получить из другой правильной несократимой дроби за 2 хода.
Решение . б) Если начальная дробь , то через три хода
Не удовлетворяет условию и натуральные числа , следовательно невозможно
за 3 хода получить дробь, равную .
0 , а за два хода , так как, Натуральные и должны удовлетворять системе " width="640"
№ 19.6
Дана правильная несократимая дробь , где и натуральные числа.
За один ход можно увеличить числитель на знаменатель, а знаменатель — на два числителя, то есть получить дробь .
в) Дробь меньше . Найдите ее наибольшее значение, которое нельзя получить из другой правильной несократимой дроби за 2 хода.
Решение . в) Несократимую дробь , за один ход можно получить из дроби
так как = 0 , а
за два хода , так как,
Натуральные и должны удовлетворять системе
№ 19.6
Дана правильная несократимая дробь , где и натуральные числа.
За один ход можно увеличить числитель на знаменатель, а знаменатель — на два числителя, то есть получить дробь .
в) Дробь меньше . Найдите ее наибольшее значение, которое нельзя получить из другой правильной несократимой дроби за 2 хода.
Решение. в)
Натуральные и должны удовлетворять системе
Так как , то наибольшее значение , которое нельзя получить из другой
правильной несократимой дроби за 2 хода .
Ответ : а) да; б) нет; в)
№ 19.7
В классе учатся мальчики и девочки, при этом в классе больше 10, но не более 26 человек, а процентная доля девочек в классе не более 21%.
а) Могло ли в классе учиться 5 девочек?
б) В класс перевелась еще одна девочка. Могла ли после этого доля девочек в классе составлять 30%?
в) Какое максимально возможное целое значение могла принимать доля девочек в классе после перевода девочки в него?
а) Да, могло. Если в классе учились 5 девочек и 20 мальчиков,
Решение .
то процентная доля девочек была равна
100% 100%
При этом условие на общее количество детей в классе выполняется
так, как .
№ 19.7
После перевода еще одной девочки в класс
В классе учатся мальчики и девочки, при этом в классе больше 10, но не более 26 человек, а процентная доля девочек в классе не более 21%.
б) В класс перевелась еще одна девочка. Могла ли после этого доля девочек в классе составлять 30%?
в) Какое максимально возможное целое значение могла принимать доля девочек в классе после перевода девочки в него?
Решение .
б) Пусть в классе учились n детей, при этом d из них — девочки.
В этом случае процентная доля девочек составляла 100%.
Начальная процентная доля девочек была не более 21% , значит,
количество девочек в классе стало равно d + 1 ,
а количество детей — n + 1 .
В этом случае процентная доля девочек составила 100%.
10 . После перевода еще одной девочки процентная доля девочек не могла составлять 30% . " width="640"
№ 19.7
После перевода еще одной девочки процентная доля девочек составила 100%.
В классе учатся мальчики и девочки, при этом в классе больше 10, но не более 26 человек, а процентная доля девочек в классе не более 21%.
б) В класс перевелась еще одна девочка. Могла ли после этого доля девочек в классе составлять 30%?
в) Какое максимально возможное целое значение могла принимать доля девочек в классе после перевода девочки в него?
Решение.
б) Пусть в классе учились n детей, при этом d из них — девочки.
, ,
что противоречит условию n 10 . После перевода еще одной девочки процентная
доля девочек не могла составлять 30% .
№ 19.7
В классе учатся мальчики и девочки, при этом в классе больше 10, но не более 26 человек, а процентная доля девочек в классе не более 21%.
в) Какое максимально возможное целое значение могла принимать доля девочек в классе после перевода девочки в него?
Решение.
в) Оценим .
10 n 11, .
.
Значит, наибольшее целое значение, которое могла принимать процентная доля
девочек, равно 27% .
— несократимая дробь, то 100 , что противоречит условию .
Значит, наибольшее целое значение, которое могла принимать процентная доля
девочек, равно 26% .
№ 19.7
В классе учатся мальчики и девочки, при этом в классе больше 10, но не более 26 человек, а процентная доля девочек в классе не более 21%.
в) Какое максимально возможное целое значение могла принимать доля девочек в классе после перевода девочки в него?
Наибольшее целое значение, которое могла принимать процентная
Решение.
в)
доля девочек, равно 26% .
— несократимая дробь, тогда
то 50 , что противоречит условию
Значит, наибольшее целое значение, которое могла принимать
процентная доля девочек, равно 25% .
№ 19.7
В классе учатся мальчики и девочки, при этом в классе больше 10, но не более 26 человек, а процентная доля девочек в классе не более 21%.
в) Какое максимально возможное целое значение могла принимать доля девочек в классе после перевода девочки в него?
Если вначале было 2 девочки и 9 мальчиков,
в)
Решение .
то исходная процентная доля девочек была равна
100% 100% 20% 21%.
После перевода еще одной девочки в класс
процентная доля девочек стала равняться
100% 100% 25%.
Ответ: а) да; б) нет; в) 25.
№ 19.8 Сборник И.В. Ященко 2024 г. Вариант 33
В школах №1 и №2 учащиеся писали тест. Из каждой школы тест писали по крайней мере 2 учащихся, а суммарно тест писал 51 учащийся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешёл из школы №1 в школу №2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе №1 вырасти в 2 раза?
б) Средний балл в школе №1 вырос на 10%, средний балл в школе №2 также вырос на 10%. Мог ли первоначальный средний балл в школе №2 равняться 1?
в) Средний балл в школе №1 вырос на 10%, средний балл в школе №2 также вырос на 10%. Найдите наименьшее значение первоначального среднего балла в школе №2.
№ 19.8 Сборник И.В. Ященко 2024 г. Вариант 33
В школах №1 и №2 учащиеся писали тест. Из каждой школы тест писали по крайней мере 2 учащихся, а суммарно тест писал 51 учащийся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешёл из школы №1 в школу №2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе №1 вырасти в 2 раза?
Решение.
а)
До перехода учащегося
Школа
До перехода учащегося
Школа
Количество учащихся, чел.
№ 1
Количество учащихся, чел.
№ 1
Средний балл
Средний балл
n
n
После перехода учащегося
После перехода учащегося
Суммарный балл
Суммарный балл
А
А
Количество учащихся, чел.
Количество учащихся, чел.
nА
nА
Средний балл
n1
Средний балл
Суммарный балл
Суммарный балл
2А
2А
2А(n1)
nА
Суммарный балл после перехода учащегося уменьшился на
Каждый учащийся набрал натуральное число баллов,
так, как n
то суммарный балл после перехода учащегося в школу №2 должен был уменьшится
на положительное число.
№ 19.8 Сборник И.В. Ященко 2024 г. Вариант 33
б) Средний балл в школе №1 вырос на 10%, средний балл в школе №2 также вырос на 10%. Мог ли первоначальный средний балл в школе №2 равняться 1?
Решение.
б) Пусть учащийся, который перешёл из школы №1 в школу №2 набрал x баллов.
Школа
Школа
До перехода учащегося
До перехода учащегося
Количество учащихся, чел.
№ 1
Количество учащихся, чел.
№ 1
n
n
Средний балл
Средний балл
Суммарный балл
Суммарный балл
После перехода учащегося
А
А
После перехода учащегося
nА
nА
Количество учащихся, чел.
Количество учащихся, чел.
n1
Средний балл
Средний балл
1,1А
1,1А
Суммарный балл
Суммарный балл
1,1А(n1)
Начальный суммарный балл в школе №1 nА = 1,1А(n1) + x.
nА = 1,1nА 1,1А + x ⇔
⇔ 10 x = А(11n)
10nА = 11nА 11А + 10 x
Так как x N, то 10x N и А(11 n) N , тогда 11 n 0 ⇔ n 11 .
№ 19.8 Сборник И.В. Ященко 2024 г. Вариант 33
б) Средний балл в школе №1 вырос на 10%, средний балл в школе №2 также вырос на 10%. Мог ли первоначальный средний балл в школе №2 равняться 1?
Решение. б) Пусть учащийся, который перешёл из школы №1 в школу №2 набрал x баллов.
Школа
Школа
До перехода учащегося
До перехода учащегося
Количество учащихся, чел.
№ 2
Количество учащихся, чел.
№ 2
51n
Средний балл
Средний балл
Суммарный балл
После перехода учащегося
В
После перехода учащегося
Суммарный балл
В
(51n)В
Количество учащихся, чел.
Количество учащихся, чел.
52n
Средний балл
Средний балл
1,1В
1,1В
Суммарный балл
Суммарный балл
1,1В(52n)
После перехода ученика суммарный балл школе №2 1,1(52n)В = (51n)В + x.
57,2 В В = 51 nВ + x ⇔
⇔ 10 x = В(62n).
nВ = 62В 10 x
По условию В = 1, 10 x = 62n. Так как n N, то (62n)10. Так как 2 то n 2 .
А(11n) = 10 x = В(62n), 9А= 60, А =
— противоречие , так как А N .
№ 19.8 Сборник И.В. Ященко 2024 г. Вариант 33
в) Средний балл в школе №1 вырос на 10%, средний балл в школе №2 также вырос на 10%. Найдите наименьшее значение первоначального среднего балла в школе №2.
в) По условию В N В 1 . Из пункта б) В 1 , тогда В = 2,
Решение.
10 x = А(11n) и
10 x = В(62n).
При В = 2 10 x = 2(62n) 5 x = 62n ) .
По доказанному ранее , тогда или = 7.
Пусть В = 2 , = 2 , тогда А(11n) = В(62n) 9А = 120 А = — противоречие ,
так как А N .
Пусть В = 2 , = 7 , тогда А(11n) = В(62n) 4А = 110 А = — противоречие , А N .
Значит В 3 , тогда minB = 3 и 10 x = В(62n) 10 x = 3(62n).
Приведем пример с В = 3.
№ 19.8 Сборник И.В. Ященко 2024 г. Вариант 33
в) Средний балл в школе №1 вырос на 10%, средний балл в школе №2 также вырос на 10%. Найдите наименьшее значение первоначального среднего балла в школе №2.
Пример с В = 3.
10 x = А(11n) ,
Решение. в)
Пусть = 2 , x = 18 , тогда средний балл A в школе №1 равен А = 20.
Пусть у перешедшего учащегося было 18 баллов, у оставшегося в школе №1 — 22 балла.
Тогда средний балл до перехода в школе №1 был равен 20. После перехода
учащегося с 18 баллами средний балл в школе №1 стал равен 22 = 1,1 20 баллам.
Пусть в школе №2 до перехода учащегося из школы №1 было 49 учащихся с баллом 3 .
Тогда средний балл в школе №2 был 3 . После перехода учащегося из школы №1
средний балл стал равен 3,3 = 1,1 .
Ответ: а) нет; б) нет; в) 3.
№ 19.9
Последовательность () состоит из 100 натуральных чисел. Каждый член последовательности, начиная со второго, либо вдвое меньше предыдущего,
либо больше его на 90.
а) Может ли такая последовательность быть образована ровно четырьмя различными числами?
б) Чему может равняться , если = 89?
в) Какое наименьшее значение может принимать самое большое из чисел такой последовательности?
Решение. а) Да, может. Пример. (): 270 , 360 , 180 , 90 , 180, 90, …
б) Если в последовательности нечётное число, а все члены натуральные числа,
то следующее за ним должно быть на 90 больше.
Если = 89 , то все числа в последовательности нечётные и
= + 99 90 = 89 + 99 90 = 8999.
96 при i 98 - чётное. Наименьшее k при , то k 7. " width="640"
№ 19.9
Последовательность () состоит из 100 натуральных чисел. Каждый член последовательности, начиная со второго, либо вдвое меньше предыдущего,
либо больше его на 90.
в) Какое наименьшее значение может принимать самое большое из чисел такой последовательности?
Решение. в)
Пример. Последовательность (): 96, 48, 24, 12, 6, … удовлетворяет
условию и наибольшее число 96. Докажем, что самое большое из чисел такой
последовательности не может быть меньше 96.
Пусть все числа в последовательности меньше 96, тогда для i
, тогда
Если - нечётное, тогда + 180 96 при i 98 - чётное.
Наименьшее k при , то k 7.
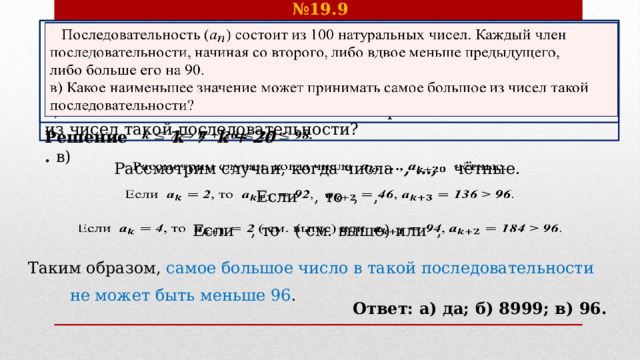
№ 19.9
Последовательность () состоит из 100 натуральных чисел. Каждый член последовательности, начиная со второго, либо вдвое меньше предыдущего,
либо больше его на 90.
в) Какое наименьшее значение может принимать самое большое из чисел такой последовательности?
k 7 k + 20
Решение. в)
Рассмотрим случаи, когда числа , …, чётные.
Если , то , ,
Если , то ( см. выше) или ,
Таким образом, самое большое число в такой последовательности
не может быть меньше 96 .
Ответ: а) да; б) 8999; в) 96.
( + + ) 3 , что противоречит условию. Аналогично рассуждая, мы можем сказать, что из этой четверки не делится на 3 . Так как числа расставлены по кругу, то для каждого числа есть две четверки, где оно первое или четвертое . Следовательно, все N чисел не делятся на 3 . Чисел от 1 до 339 , делящихся на 3 , 113 штук. Следовательно, не кратных 3 — 226 штук, что меньше 240 . Ответ: нет, не может. " width="640"
№ 19.10 ЕГЭ-2022, Дальний Восток
По кругу расставлены N чисел, меньших 340, так, что сумма трех последовательных чисел не делится на 3, а сумма четырех последовательных делится на 3.
а) Может ли N быть равно 240?
По кругу расставлены N чисел, меньших 340, так, что сумма трех последовательных чисел не делится на 3, а сумма четырех последовательных делится на 3.
а) Может ли N быть равно 240?
б) Может ли N быть равно 129?
в) Какое наибольшее значение может принимать N?
Решение. а) Рассмотрим четыре подряд идущих числа , , ,
Если бы ai 3 , то из ( + + + ) 3 = ( + + ) 3 ,
что противоречит условию.
Аналогично рассуждая, мы можем сказать, что из этой четверки не делится на 3 .
Так как числа расставлены по кругу, то для каждого числа есть две четверки, где оно
первое или четвертое . Следовательно, все N чисел не делятся на 3 .
Чисел от 1 до 339 , делящихся на 3 , 113 штук.
Следовательно, не кратных 3 — 226 штук, что меньше 240 .
Ответ: нет, не может.
№ 19.10 ЕГЭ-2022, Дальний Восток
По кругу расставлены N чисел, меньших 340, так, что сумма трех последовательных чисел не делится на 3, а сумма четырех последовательных делится на 3.
б) Может ли N быть равно 129?
Решение. б)
Из пункта а) все N чисел не делятся на 3 .
Значит, могут быть только остатки 1 и 2 , т. е. на круге все числа вида 3m + 1 или 3m + 2 ..
По условию любые три подряд идущие числа не делятся на 3 , значит,
числа вида 3m + 1 не стоят три подряд , а стоят через одно или через два .
Аналогично, числа вида 3m + 2 не стоят три подряд , а стоят через одно или через два .
№ 19.10 ЕГЭ-2022, Дальний Восток
…
…
…
…
По кругу расставлены N чисел, меньших 340, так, что сумма трех последовательных чисел не делится на 3, а сумма четырех последовательных делится на 3.
б) Может ли N быть равно 129?
Обозначим числа, дающие при делении на 3 остаток 1 , как (1) .
Решение. б)
Числа, дающие при делении на 3 остаток 2 , обозначим как (2) .
Получим варианты:
Других вариантов нет , так как сумма чисел в четверке
Вариант 1
Вариант 2
(1)
(1)
(1)
(2)
должна быть кратна трем .
(2)
(2)
(1)
(2)
(2)
Это значит, что если в ней 2 числа типа (1) ,
(2)
(1)
(1)
(2)
то должно быть и 2 числа типа (2 ) .
(1)
(1)
(1)
(2)
(2)
№ 19.10 ЕГЭ-2022, Дальний Восток
…
…
…
…
По кругу расставлены N чисел, меньших 340, так, что сумма трех последовательных чисел не делится на 3, а сумма четырех последовательных делится на 3.
б) Может ли N быть равно 129?
Вариант 2
Вариант 1
Решение. б)
(1)
(1)
(2)
(1)
Если где-то рядом стоят 1,2,
Если где-то стоят рядом
(2)
(2)
(1)
то по краям от них стоят
две единицы, то
(2)
(2)
(2)
1 и 2 , то есть имеем либо
справа и слева
(1)
(1)
(1)
четверку 1 , 1 , 2 , 2 , либо 2,1,2,1 .
(1)
(2)
от 1,1 должны быть 2,2 .
(2)
(1)
(2)
Тогда числа можно разбить на пары вида 1,2 .
Следовательно, единиц и двоек
должно быть четно , значит и
Однако 129 чисел нельзя разбить на пары .
всех чисел должно быть четно .
129 нечетно .
Ответ : нет, не может.
№ 19.10 ЕГЭ-2022, Дальний Восток
…
…
По кругу расставлены N чисел, меньших 340, так, что сумма трех последовательных чисел не делится на 3, а сумма четырех последовательных делится на 3.
в) Какое наибольшее значение может принимать N?
Решение. в)
Из пункта а) получаем оценку на количество чисел N ≤ 226 .
А в пункте б) мы получили, что количество чисел четно ,
следовательно, наибольшее возможное значение N равно 226 .
Пример.
Числа от 1 до 338 в порядке возрастания,
1
2
338
4
337
исключив из них делящиеся на 3 ,
5
7
что соответствует последовательности остатков
8
..., 1, 2, 1, 2, 1, 2, ...
10
11
Ответ: нет; нет; 226.
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
Закрыть через 5 секунд
