Презентация к итоговому уроку по теме " Производная и ее применение"

Производная и ее применение

Скажи мне, и я забуду.

Покажи мне, и я запомню.

Вовлеки меня, и я научусь.

Содержание диктанта

1 вариант

2 вариант

y = sin x

y' (0) - ?

у = tgx y'(0)-?

y=2 +4

y= (x-3) 5

y' (1) - ?

y= -

y=

y' (4) - ?

y=

y'(1)-?

y=ln(3x-9) y'(4)-?

y=

y' (3) - ?

y'(3)-?

y= y'(3)-?

y' (0) - ?

Задача №1.

Найти промежутки возрастания и убывания функции у = lnх +

Задача №2.

Найти наибольшее значение функции

у = 19 – 2 cos х - на отрезке [- ]

Задача №3.

Составить уравнение касательной к графику функции f (х) = ln (2е - х) в точке х 0 = е

Задача №4.

Тело движется по прямой так, что расстояние S до него от некоторой точки А этой прямой изменяется по закону

S = 0,5 t 2 +3 t + 2 , где t – время движения. Через какое время после начала движения скорость тела окажется равной 15м/с?

Карточка 1

1. Расшифруйте, как И. Ньютон называл производную функцию.

С

Я

Ю

Ф

К

И

Л

1

3

-3/2

-4

-1

-3

-5

Карточка 2

1. Решив эти примеры, вы расшифруете фамилию французского математика, который ввел термин .

Р

Н

Г

А

Ж

А

Л

-1

-5

1

12

2

1/6

Карточка 3

1. Решив эти примеры, вы узнаете, как И. Ньютон называл функцию

А

Л

Н

Е

Т

Ф

Ю

3

5

-3

2

1/6

-5

1

Карточка 4

1. Решив эти примеры, вы узнаете фамилию ученого, который вывел формулы, связывающие тригонометрические функции с показательной

Й

Е

Э

Р

Л

e/3

1872

-2

32/3

57,5

Производная и ее применение

Производной функции f(х) в точке х 0 называется предел отношения приращения функции Δf = f(х 0 + Δх) – f(х 0 ) к приращению аргумента Δх при Δх →0, если этот предел существует: f' (х 0 ) =

Геометрический смысл производной заключается в том, что значение производной функции в точке х равно угловому коэффициенту касательной к графику функции в точке (х, f (x))

Уравнение касательной к графику функции y = f (х) в точке х 0 :

у = f (х 0 ) + f ' (х 0 )(х-х 0 )

Алгоритм нахождения уравнения касательной к графику функции

Этапы

Пример: для функции у= найти уравнение касательной в точке х 0 = 1

1. Найти значение функции в точке х 0

f(x 0 ) = f (1) = 1

• Найти производную функции

f ' (х)

f ' (x) = ( )' =

3. Найти значение производной в точке х 0 = 1

f ' (x 0 ) = f (1) =

4. Составить уравнение касательной к графику функции

У = 1 + (х-1) = х +

  Вторая производная

Второй производной функции у = f (х) называется производная от производной f' (х) (обозначается f '' (х)).

Физический смысл производной

Если точка движется вдоль оси х и ее координата изменяется по закону х (t), то мгновенная скорость точки

v(t)= = x' (t),

а ускорение :

a (t)=

0, то функция f (х) монотонно возрастает на этом интервале. Достаточное условие убывания функции: если в каждой точке интервала (а,b) f ' (x) Необходимое и достаточное условие постоянства функции: функция f (x) постоянна на интервале (а; b) тогда и только тогда, когда f ' (x) = 0 в каждой точке этого интервала. " width="640"

  Исследование функции монотонность

Достаточное условие возрастания функции : если в каждой точке интервала (а,b) f ' (x) 0, то функция f (х) монотонно возрастает на этом интервале.

Достаточное условие убывания функции: если в каждой точке интервала (а,b) f ' (x)

Необходимое и достаточное условие постоянства функции: функция f (x) постоянна на интервале (а; b) тогда и только тогда, когда f ' (x) = 0 в каждой точке этого интервала.

0 при х f ' (х) х 0 , Если f '(х)то х 0 – точка максимума. f ' (х) 0 при х х 0 , то х 0 – точка минимума . " width="640"

  Экстремумы Необходимое условие экстремума

Если х 0 – точка экстремума функции у = f (x), то эта точка является критической точкой данной функции, то есть в этой точке производная либо равна нулю, либо не существует.

Достаточное условие экстремума

Если функция у = f(х) непрерывна в точке х 0 и производная f ' (x) меняет знак в этой точке, то х 0 - точка экстремума функции у = f(х).

Если f ' (х) 0 при х

f ' (х) х 0 ,

Если f '(х)

то х 0 – точка максимума.

f ' (х) 0 при х х 0 ,

то х 0 – точка минимума .

  Алгоритм нахождения интервалов монотонности и экстремумов

Этапы

Пример для функции у = 2х 3 – 3х 2 – 36х +5

1.Найти область определения функции и интервалы, на которых функция непрерывна

2.Найти производную f (х)

Область определения: R

Функция непрерывна на всей области определения

f ' (х) = 6х 2 – 6х – 36

3.Найти критические точки, т.е. точки, в которых производная функции равна нулю или не существует

f ' (х) = 0 при х = -2, х = 3

4.В каждом из интервалов, на которые область определения разбивается критическими точками, определить знак производной и характер изменения функции

5.Относительно каждой критической точки определить , является ли она точкой максимума, минимума или не является точкой экстремума

знак f

_+______-__________+______

Х = -2 точка максимума

6.Записать результат исследования функции: промежутки монотонности и экстремумы.

-2 3

Х = 3 точка минимума

f(х) возрастает при х є (-∞;- 2) и при х є (3;∞); f(х) убывает при х є (-2; 3);

х max = -2, у max = f (-2) = 49; х min =3, у min = f(3) = -76

Наибольшее и наименьшее значения функции

Функция, непрерывная на отрезке, достигает своего наибольшего и наименьшего значений на этом отрезке либо в критических точках, принадлежащих отрезку, либо на его концах.

Алгоритм нахождения наибольшего и наименьшего значений функции, непрерывной на отрезке

Этапы

Пример: для функции

1.Найти производную f ' (х)

у = 2х 3 – 3х 2 – 36х +5 на отрезке [0;4]

f ' (х) = 6х 2 – 6х – 36

2.Найти на данном отрезке критические точки, т.е точки, в которых f ' (х) = 0 или не существует

3.Вычислить значения функции в критических точках, принадлежащих этому отрезку и на концах отрезка.

f ' (х) = 0 при х = -2, х = 3

отрезку [0;4] принадлежит только одна критическая точка: х = 3

f (0) = 5

4.Из вычисленных значений выбрать наименьшее и наибольшее

f(3) = -76

max f (x) = f (0) = 5

f (4) = -59

min f (x) = f(3) = -76

  Применение производной к исследованию функции

Схема исследования функции

При исследовании свойств функции полезно найти:

- область ее определения;

- производную;

- критические точки;

- промежутки возрастания и убывания;

- точки экстремума и значения функции в этих точках.

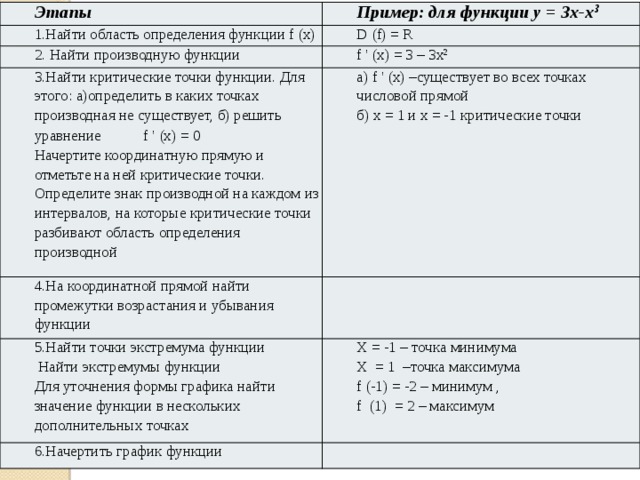
Этапы

1.Найти область определения функции f (х)

Пример: для функции у = 3х-х 3

D (f) = R

2. Найти производную функции

f ' (x) = 3 – 3x 2

3.Найти критические точки функции. Для этого: а)определить в каких точках производная не существует, б) решить уравнение f ' (х) = 0

4.На координатной прямой найти промежутки возрастания и убывания функции

а) f ' (x) –существует во всех точках числовой прямой

Начертите координатную прямую и отметьте на ней критические точки. Определите знак производной на каждом из интервалов, на которые критические точки разбивают область определения производной

б) х = 1 и х = -1 критические точки

5.Найти точки экстремума функции

Найти экстремумы функции

Х = -1 – точка минимума

6.Начертить график функции

Х = 1 –точка максимума

Для уточнения формы графика найти значение функции в нескольких дополнительных точках

f (-1) = -2 – минимум ,

f (1) = 2 – максимум

Спасибо за внимание !