Презентация к проекту "Красивые задачи в математике"

«Красивые» задачи в математике

«Красивые» задачи

в математике

Автор: Назаренко Наталья

Ученица 9 класса МБОУ ООШ № 46

Авторы:

Битюцкая Анастасия 10Б

Красовская Виктория 9Б

Тимошенкова Любовь 10Б

Руководитель : Дериболот М.И.,

учитель математики

Цель работы: создать сборник «красивых» математических задач .

Задачи:

• Изучение научной литературы, научных публикаций по данной теме, анализ полученной информации.
• Определение понятия «красивая» задача в математике.
• Классификация найденных задач по разделам.
• Создание сборника «красивых» математических задач.

Гипотеза: если окажется возможным из множества математических задач выбрать определенные («красивые») задачи и классифицировать их по некоторым признакам, то возможно создание сборника таких задач и использование его в качестве пособия для математического саморазвития.

• Объект исследования
• - решение математических задач.
• Предмет исследования
• - математические задачи определенного типа.

Объектная область

исследования

– учебный предмет «математика».

Методика исследования:

- изучение литературы;

- «красивые» задачи в математике;

- беседы;

- опросы;

- анкетирование.

Требования к «красивым» задачам:

• интересное условие, красивый чертеж;
• нестандартный элемент (в условии, в методах решения);
• установление интересного факта;
•   доступность по формулировке и по сложности;
• изюминка в решении (наглядность и простота.

«Красивые» задачи в математике делим на:

«Красивые» задачи по содержанию;

  «красивые» задачи по чертежу;

«красивые» задачи по решению;

  «красивые» олимпиадные задачи;

  «красивые» экономические задачи.

«Красивые» задачи по содержанию Задача Кольцо вокруг Земли

• Образно представьте себе нашу планету, плотно стянутую кольцом по всему ее экватору. После увеличения длины окружности кольца на 10 метров, между кольцом и поверхностью земли образовался зазор определенной величины. Сможет ли человек пройти, или хотя бы протиснуться в этот зазор?

Решение

Известно, что экватор имеет длину приблизительно равную 40000 километров.

Изначально может показаться, что увеличение длины кольца на 10 метров, по сравнению с его длиной в 40 000 км будет способствовать образованию практически незаметного зазора. Однако, исходя из формулы определения длины окружности L=2πR видно, что радиус Земли (кольца) R= L/2π   и при увеличении длины кольца на 10м, его радиус приблизительно увеличиться на 1,59м (10м/6,28), образуя соответствующий зазор, в который человек сможет не только протиснуться, но и даже пройти, немного нагнувшись.

«Красивые» задачи по содержанию древнегреческая Задача

• -Скажи мне, знаменитый Пифагор, сколько учеников посещают твою школу и слушают твои беседы.
• -Вот сколько, - ответил Пифагор, - половина изучает математику, четверть - природу, седьмая часть проводит время в размышлении и, кроме того, есть три женщины.

Решение

Пусть х  всего человек. По условию задачи составим уравнение.

1/2•х+1/4•х+1/7•х+3 = х |•28

14•х+7•х+4•х+84 = 28х

3х =84

х  = 28

28 учеников посещают школу

Ответ.28 человек.

«Красивые» задачи по содержанию Древнеиндийская Задача

Над озером тихим

С полфута размером

Высился лотоса цвет.

Он рос одиноко,

И ветер порывом

Отнёс его в сторону. Нет

Боле цветка над водой.

Нашёл же рыбак его

Ранней весною

В двух футах от места, где рос.

Итак, предложу я вопрос:

“ Как озера вода здесь глубока?”

Какова глубина озера в современных единицах длины (1 фут приближённо равен 0,3 м)?

Обозначим глубину озера АС =Х, тогда AD = AB = Х + 0,5 .

Из треугольника ACB по теореме Пифагора имеем AB 2 – AC 2 = BC 2 ,

(Х + 0,5) 2 – Х 2 = 2 2 ,

Х 2 + Х + 0,25 – Х 2 = 4,

Х = 3,75.

Таким образом, глубина озера составляет 3,75 фута.

3, 75 • 0,3 = 1,125 (м)

Ответ: 3,75 фута или 1, 125 м.

«Красивые» задачи по чертежу Задача

• Зигзаг разделил правильный девятиугольник на треугольники, как показано на рисунке. Какая часть площади больше: закрашенная или не закрашенная?

Решение.

Проведем в девятиугольнике еще несколько диагоналей.

Девятиугольник разбился на 13 треугольников. На рисунке образовалось много параллелограммов и трапеций с диагоналями. Расставим номера треугольников, причем одинаковым номером отметим равные треугольники разных цветов. 12 из них разбились на пары, а тринадцатому, который оказался закрашенным, пары не хватило. Значит, закрашенная часть площади девятиугольника больше его не закрашенной части.

Ответ: закрашенная.

«Красивые» задачи по чертежу Задача

• Все углы в шестиугольнике ABCDEF равны по 120 градусов. Известно, что EF=1, AB=3, BC=4, CD=1. Найдите AF+DE.

Решение.

Продлим стороны FA, СВ и ED. В этом случае к нашему шестиугольнику дополнительно прикрепятся 3 треугольника. Определим их вид.

Так как все внутренние углы шестиугольника равны по 120 градусов, то все внешние с ними углы содержат по 60 градусов последний угол в каждом треугольнике равен 60 град. и — равносторонние. Отсюда можно сделать вывод, что CN=ND=5, AK=BK=3 и MF=EM=1. Тогда KM=3+4+5=12.

Пользуемся тем, что MN=KN=12 получаем, что

ED=MN-ME-DN=12-1-5=6

AF=MK-MF-AK=12-1-3=8

Теперь проще простого найти нужную сумму: ED+AF=6+8=14

Ответ: 14

«Красивые» задачи по чертежу Задача

• Два противоположных ребра единичного куба лежат в основаниях цилиндра, а остальные вершины – на его боковой поверхности. Одна из граней куба образует с основаниями цилиндра угол .  (  90º). Найдите высоту цилиндра.

Решение.

Рассмотрим плоскость, проходящую через прямую АВ и образующую l . Пусть грань ABCD образует с плоскостью нижнего основания угол  , тогда  ВАЕ   . Высота цилиндра состоит из двух отрезков FB и BE. Найдем длины этих отрезков.

Из прямоугольного треугольника АВЕ: ВЕ=1•sin  = sin  . Заметим, что в прямоугольном треугольнике OFB:  FBO=  , значит FB=1•cos  = cos  . Итак, FE=FB+BE=cos  +sin  .

Ответ: cos  +sin  .

«Красивые» задачи по решению Задача

• В XIX веке один учитель задал своим ученикам вычислить сумму всех целых чисел от единицы до ста. Компьютеров и калькуляторов тогда еще не было, и ученики принялись добросовестно складывать числа. И только один ученик нашел правильный ответ всего за несколько секунд. Им оказался Карл Фридрих Гаусс - будущий великий математик. Как он это сделал?

Решение

Он выделил 49 пар чисел: 99 и 1, 98 и 2, 97 и 3 ... 51 и 49. В сумме каждая пара чисел равнялась ста, и оставалось два непарных числа 50 и 100. Следовательно, 49х100+50+100=5050.

Ответ: 5050.

«Красивые» задачи по решению Задача о пяти линиях

• Перед вами пять линий и десять кружков. Нужно разместить кружки и линии так, чтобы на каждой линии было по четыре кружка и вместе с тем линии должны образовать законченную геометрическую фигуру, хорошо знакомую каждому человеку. Как расположить линии, чтобы на каждой из них было по четыре кружка?

Ответ: Линии выкладываются в виде звезды, как показано на рисунке.

«Красивые» задачи по решению Задача

• Дан острый угол А, вершина которого недоступна (находится за пределами чертежа). Постройте биссектрису данного угла.

Решение.

Факт: три биссектрисы треугольника пересекаются в одной точке. Взяв две произвольные точки В и С на сторонах данного угла, получим треугольник АВС (с одной недоступной вершиной), две биссектрисы которого можно построить. Точка пересечения этих биссектрис лежит на искомой биссектрисе. Аналогично можно найти и вторую точку, выбрав другой треугольник.

«Красивые» олимпиадные задачи Задача

• Дана белая доска размером 100*100 клеток. Двое по очереди красят ее клетки в черный цвет, причем первый всегда закрашивает квадрат 2*2, а второй — три клетки, образующие «уголок». Уже покрашенную клетку второй раз красить нельзя. Проигрывает тот, кто не может сделать очередной ход. Кто выигрывает при правильной игре: первый или второй?

Решение.

В одном из углов доски второй игрок своим первым ходом закрашивает три клетки в прямоугольнике 2x3, а три оставшиеся клетки из этого прямоугольника объявляет резервом (рис. 10). В дальнейшем второй игрок делает все возможные ходы, не затрагивая резерва. Если такой ход становится невозможным, то закрашиваются клетки резерва. Ясно, что ответного хода у первого игрока нет.

Ответ: второй

«Красивые» олимпиадные задачи Задача

• Дана возрастающая арифметическая прогрессия с положительными членами. Определить их количество, если известно, что сумма членов прогрессии с нечётными номерами составляет 52% от общей суммы всех членов этой прогрессии?

Решение.

Сразу обратим внимание, что количество членов этой прогрессии не может быть чётным. В противном случае сумма её членов с нечётными номерами была бы меньше суммы её членов с чётными номерами, поскольку прогрессия возрастающая.

Обозначим искомое число членов прогрессии за . Тогда сумма её членов с нечётными номерами равна

А сумма всех членов прогрессии равна:

Тогда имеет место равенство:

Из последнего уравнения получаем n=25 .

Ответ: 25.

«Красивые» олимпиадные задачи Задача «Волк, коза и капуста»

Старику необходимо переправить через реку капусту, козу и волка. Но дело в том, что в лодке кроме самого старика, есть ещё одно место для капусты, козы или волка. Если старик оставит козу с волком, то волк может съесть козу, а если оставить капусту с козой, то она съесть капусту. В присутствии старика никто никого не ест. Подскажите ему способ переправы на другой берег всех.

волк капуста

коза

коза



волк



волк коза

капуста

коза

коза капуста

коза



капуста

волк





капуста волк



коза

капуста волк коза



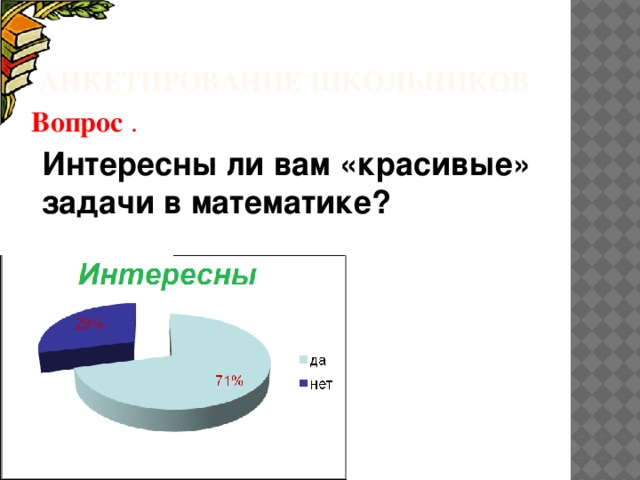
Анкетирование школьников

Вопрос .

Интересны ли вам «красивые» задачи в математике?

Вопрос №2. Удобен ли сборник по изучению «Красивых» задач в математике?

Результаты исследований

  В результате исследования выявлено, что:

• 71 % учащихся интересно изучать «красивые» задачи;

2. 86 % учащихся удобно пользоваться м сборником по изучению «красивых» задач в математике.

Выводы:

Анализ анкет подтвердил, что большинство учащихся нашего класса интересуются изучением «красивых» задач в математике и создание сборника «красивых» математических задач – актуально

Заключение

• Работа по выбранной теме осуществлялась в полном соответствии с планом исследования.
• В ходе исследования дано определение «красивой» математической задачи, проведена классификация таких задач по определенным признакам.
• Изучена литература по вопросу исследования.
• Идет работа над созданием сборника «красивых» математических задач

Спасибо!