Презентация к работе "Загадочная лента Мебиуса"

Районная конференция

«Старт в науку»

Номинация: МАТЕМАТИКА

Тема работы:

«Загадочная лента Мебиуса»

Автор: Новоселова Анастасия

Ученица 7-а класса

Руководитель проекта Вакуленко Е.Ю.

Проблема:

Узнать, что такое «лист Мёбиуса» и как его можно использовать.

Гипотезы исследования:

Вероятно Мёбиус-это учёный.

А что если лист Мёбиуса растёт на дереве «Мёбиус»?

Скорей всего на листе Мёбиуса можно писать, делать рисунки, резать

его на части.

Возможно, лист Мёбиуса применяется в технике и искусстве.

Цель:

Выяснить, что такое Мёбиус?

Задачи исследования:

1.Прочитать математическую литературу, в которой авторы рассказывают о таком объекте как «Мёбиус», исследовать полученную информацию.

2.Познакомиться со свойствами листа Мёбиуса.

3. Выяснить, где применяется лист Мёбиуса.

4.Изучить опыты с листом Мёбиуса, которые описываются в математической литературе и провести эксперименты.

Официальный термин.

Ле́нта Мёбиуса (лист Мёбиуса, петля́ Мёбиуса) — топологический объект, простейшая неориентируемая поверхность с краем, односторонняя при вложении в обычное трёхмерное евклидово пространство.

Топология

В ходе исследования я узнала, что Мёбиуса считают основателем топологии.

Лист Мёбиуса — один из объектов области математики под названием «топология» (по-другому — «геометрия положения»).

В топологии изучаются свойства фигур и тел, которые не меняются при их непрерывных деформациях (как если бы они были сделаны из резины).

Замечательные ученые

Лента Мёбиуса была открыта независимо немецкими математиками Августом Фердинандом Мёбиусом и Иоганном Бенедиктом Листингом в 1858 году. Листинг опубликовал свою работу, на три года раньше Мебиуса, но лента была названа именем второго

Мёбиус

Листинг

Создание ленты

Свойства ленты

Односторонность Непрерывность Двусвязность Отсутствие ориентированности.

Односторонность

У листа Мёбиуса – всего одна сторона. Убедиться в односторонности листа Мёбиуса несложно: если начать постепенно окрашивать его в какой-нибудь цвет, начиная с любого места, и по завершении работы вы обнаружите, что весь он полностью окрашен. ‘

Вот, картинка иллюстрирующая односторонность петли мебиуса

Непрерывность

На листе Мёбиуса любая точка может быть соединена с любой другой точкой и при этом муравью на гравюре Эшера ни разу не придётся переползать через край «ленты». Разрывов нет – непрерывность полная.

Двусвязность

Лист Мёбиуса конечно двусвязен, т.к. если разрезать его вдоль, он превратится не в два отдельных кольца, а в одну целую ленту.

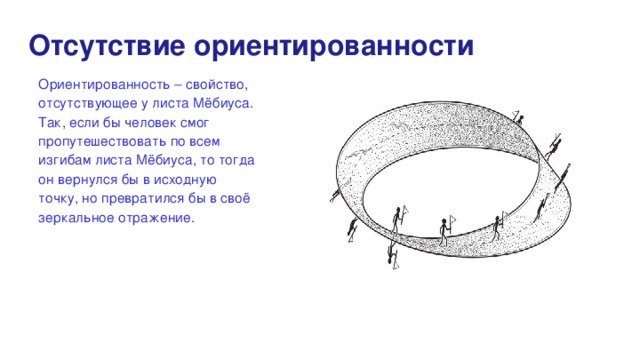
Отсутствие ориентированности ориентированности

Ориентированность – свойство, отсутствующее у листа Мёбиуса. Так, если бы человек смог пропутешествовать по всем изгибам листа Мёбиуса, то тогда он вернулся бы в исходную точку, но превратился бы в своё зеркальное отражение.

Лента Мёбиуса в...

Спираль ДНК

Есть предположение, что спираль ДНК сама по себе тоже является фрагментом ленты Мебиуса и только поэтому генетический код

так сложен для расшифровки и восприятия. Больше того - такая структура объясняет причину наступления биологической смерти

- спираль замыкается сама на себя

и происходит самоуничтожение.

В жизни.

- полоса ленточного конвейера, шлифовальная лента, выполненная в виде ленты Мёбиуса, позволяет ему работать дольше, потому что вся поверхность ленты равномерно изнашивается.

- в системах записи на непрерывную плёнку применялись ленты Мёбиуса (чтобы удвоить время записи).

- в матричных принтерах красящая лента имела вид листа Мёбиуса для увеличения срока годности. Это дает ощутимую экономию.

Живописи

Лента Мёбиуса вдохновляющая многих художников своей таинственность. Она лежит в основе некоторых картин знаменитых художников

Живописи

Скульптура

Опыт воссоздания ленты Мёбиуса интересен не только художникам, но и архитекторам и скульпторам

Скульптура

Архитектура

Маркетинг

Всем известный знак, тоже лента Мёбиуса. А вы об этом задумывались?

Фокусы

Фокусники полюбили ленту Мёбиуса, за свои удивительные свойства.

Эти фокусы точь-в-точь наши опыты, но они очень удивляли зрителей

Опыты

С лентой Мебиуса можно проводить множество экспериментов, чем мы собственно и займёмся

Опыты

№

Суть опыта

Полученный результат

Что получится, если начать закрашивать лист Мёбиуса с одной стороны, не переходя через край, какая часть ленты окажется закрашенной?

весь лист полностью окрашен

Что произойдёт с обычным кольцом, если его разрезать посередине?

два отдельных обычных кольца

если лист Мёбиуса разрезать посередине

Результат разрезания кольца посередине – одно кольцо.

Каков результат разрезания листа Мёбиуса на 3 полоски?

получается 2 кольца. Одно из них вдвое длиннее первоначальной ленты и вдвое перекручено.

Разрезаем его по пунктиру (на 5 полосок).

получим 3 кольца: I — лист Мёбиуса — 1 перекрут, ширина 1 см, длина равна длине исходного кольца. II, III — кольца с двумя перекрутами, ширина 1 см, длина в 2 раза больше исходного листа. II и III кольцо сцеплены с I кольцом и между собой.

Выводы .

Поставленной цели я достигла, так как я теперь знаю, что Мёбиус – это великий немецкий учёный, который внёс огромный вклад в развитие науки. Таким образом, получается, что верна первая гипотеза, а предположение что лист Мёбиуса растёт на дереве «Мёбиус» совершенно не верно. Ещё по ходу исследования я узнала, что наука топология – это раздел математики, изучающий явление непрерывности и познакомилась со свойствами листа Мёбиуса. Предположение о применении листа Мёбиуса (ленты Мёбиуса) в технике и искусстве оказалось верным. Ленту Мёбиуса можно встретить в различных сферах деятельности человека. Гипотеза о том, что на листе Мёбиуса можно писать, делать рисунки, резать его на части – верна частично. Ведь писать и рисовать удобнее в тетради и альбоме, а вот разрезая его на части можно проводить различные увлекательные эксперименты.

Заключение

Несмотря на то, что Мёбиус сделал своё удивительное открытие очень давно, оно очень популярно и в наши дни: У математиков - идут дальнейшие исследований

У школьников - очень интересно экспериментировать с лентой Мёбиуса; учителей – есть ещё один способ заинтересовать учеников математикой; В технике – открываются всё новые способы использования ленты Мёбиуса. Мёбиус повлиял не только на математиков, но и на художников, скульпторов, архитекторов и многих, многих, многих…

«Мышление начинается с удивления»,- заметил 2500 лет назад Аристотель. А математика замечательный предмет для удивления. В ходе математического исследования я узнала много нового и интересного, необычного. Чтобы проверить свои гипотезы, я читала книги, работала с различными источниками информации в сети Интернет, проводила эксперименты.

Спасибо за внимание!