Презентация к уроку геометрии 6 класс "Золотое сечение"

Золотое сечение в нашей жизни

Цели и задачи

Цель данной работы – изучение золотого сечения.

Задачи: познакомиться с историей возникновения золотого сечения; показать деление отрезка в золотой пропорции, построить золотой треугольник; исследовать опытным путём стремление людей и природы к гармонии и совершенству; установить области применения золотого сечения.

«…Геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением, и если первое из них можно сравнить с мерой золота, то второе – с драгоценным камнем…», - эти слова сказал четыре столетия назад немецкий астроном и математик Иоганн Кеплер, они являются эпиграфом практически ко всем трудам, посвященным «золотому сечению».

Математики установили, что примерное значение идеальной пропорции «золотого сечения» равняется 1,618... Полученное значение есть знаменитое число «фи», названное так американским математиком Марком Барром по первой букве имени великого скульптора Фидия, который, по преданию, использовал «золотое сечение» в своих работах.

Золотое сечение - это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему a : b = b : c или с : b = b : а .

История возникновения золотого сечения

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик. Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.

В фасаде древнегреческого храма Парфенона присутствуют золотые пропорции.

В средневековой Европе с золотым делением познакомились по арабским переводам “Начал” Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.

В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве.

Переходя к примерам “золотого сечения” в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи. Композиция портрета «Джоконда» построена на"золотых треугольниках".

Ощущение динамики, волнения проявляется, пожалуй, сильней всего в другой простой геометрической фигуре - спирали. Многофигурная композиция, выполненная в 1509 - 1510 годах Рафаэлем названа "Избиение младенцев".

Геометрические построения

Золотое сечение отрезка АВ:

1. В точке В восстанавливают перпендикуляр к АВ;

2. Откладывают на нём отрезок , равный половине АВ;

3. На отрезке АС откладывают отрезок СD = ВC;

4. На отрезке АВ откладывают отрезок АЕ = АD;

5. Точка Е делит отрезок АВ в отношении золотой пропорции.

Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE = 0,618..., если АВ принять за единицу, ВЕ = 0,382... Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям.

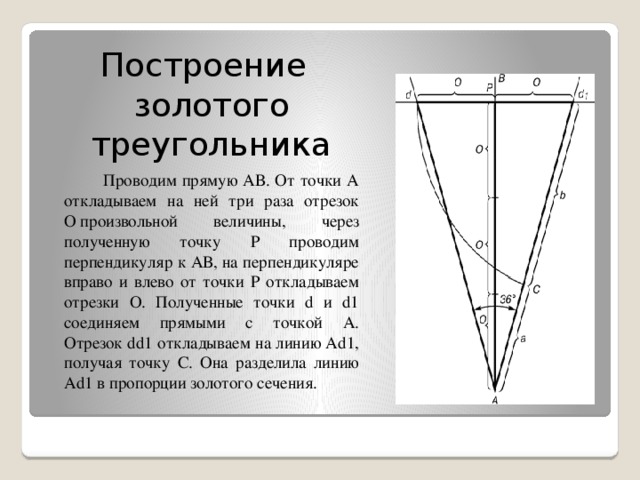
Построение золотого треугольника

Проводим прямую АВ. От точки А откладываем на ней три раза отрезок О произвольной величины, через полученную точку Р проводим перпендикуляр к АВ, на перпендикуляре вправо и влево от точки Р откладываем отрезки О. Полученные точки d и d1 соединяем прямыми с точкой А. Отрезок dd1 откладываем на линию Ad1, получая точку С. Она разделила линию Ad1 в пропорции золотого сечения.

Из выше сказанного можно сделать выводы о том, что принципы золотого сечения используются во всех областях деятельности человека. Знакомство с принципами «золотого сечения» помогает видеть гармонию и целесообразность окружающих нас творений природы и человека. Золотое сечение – это один из основных основополагающих принципов природы; человеческое представление о красивом явно сформировалось под влиянием того, какой порядок и гармонию человек видит в природе.