Презентация к уроку информатики на тему "упрощение логических выражений"

Упрощение логических выражений

10 класс

Учитель математики и информатики

МОБУ Стогинской СШ Ярославской области

Киселева И.В.

Проверка д/з

математика

1 урок

2 урок

информатика

физика

3 урок

Ответ

• Информатика

• Математика

• Физика

• Математика

• Физика

• Информатика

Закон

Для умножения

Двойного отрицания

Для сложения

Исключение третьего

Исключение констант

Повторения

Поглощения

Переместит.

Сочетат.

Распределит.

де Моргана

№ 1.Упростите выражение

№ 2.Упростите выражение

№ 3. Упростите выражение

№ 5.Упростите выражение

д/з

• Упростите:

• Докажите:

В каждой из двух аудиторий может находиться либо каб. Информатики, либо каб. Физики. Таблички: на первой - «По крайне мере в одной из аудиторий размещается кабинет информатики», на второй - «Кабинет физики находится в другой аудитории». Известно, что надписи либо обе Истинны, либо обе Ложны. Найдите кабинет информатики.

В=1 и

Решение.

А=«В 1-ой ауд. каб. Информатики»

В=«Во 2-ой ауд. каб. Информатики»

=«В 1-ой ауд. каб. Физики»

=«Во 2-ой ауд. каб. Физики»

• X=(АvB)
• Y=Не А

Ответ: «В 1-ой ауд. каб. Физики»

«Во 2-ой ауд. каб. Информатики»

Переведите высказывания на язык алгебры логики:

а) (Аv  A)&B=1&B=B

б) (A&(AvB)&(Bv  B)=A&(AvB)&1=A&(A&B)

Равносильность логических выражений

10 класс

Логические выражения, у которых последние столбцы в таблице истинности совпадают, называются равносильными .

Обозначение “=“

Докажите равносильность

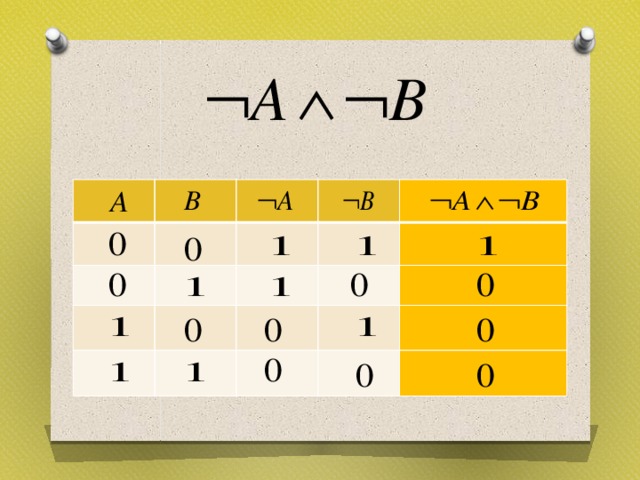
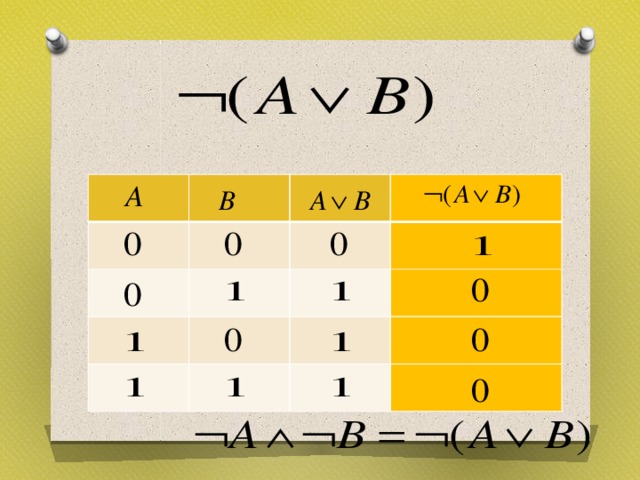
Самостоятельная работа

Вариант 1 № 1 В № 2 А^В

Вариант 2 № 1 В № 2 А или В

Вариант 3 № 1 А^В № 2 А

Вариант 4 № 1 А или В № 2 А^В

Самостоятельная работа

Вариант I

Вариант II

• Постройте ТИ выражения

• Постройте ТИ выражения

• Докажите равносильность

• Докажите равносильность

Проверка

Вариант II

Вариант I

ТИ

ТИ

Молодцы