Презентация к уроку: "КОМБИНАЦИИ МНОГОГРАННИКОВ И ТЕЛ ВРАЩЕНИЯ"

КОМБИНАЦИИ МНОГОГРАННИКОВ И ТЕЛ ВРАЩЕНИЯ

МНОГОГРАННИКИ

Многогранник  или  полиэдр  — обычно замкнутая поверхность, составленная из многоугольников, но иногда так же называют тело, ограниченное этой поверхностью.

2/18/17

2/18/17

ПРИЗМА

Призма   многогранник, две грани

которого являются конгруэнтными

(равными) многоугольниками,

  лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками. Эти параллелограммы называются  боковыми гранями  призмы,

  а оставшиеся два многоугольника называются её  основаниями .

2/18/17

2/18/17

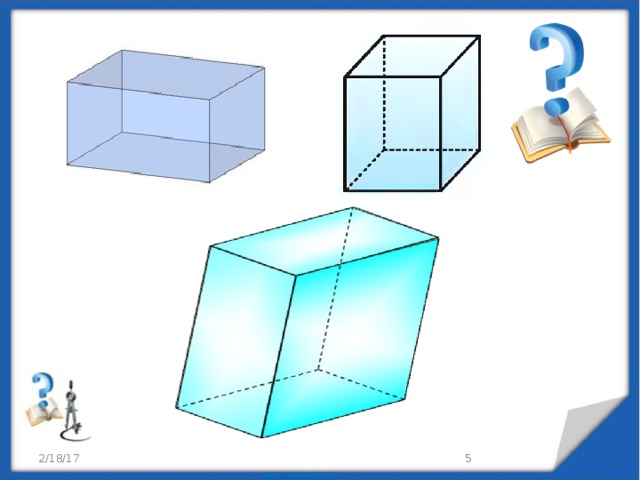
Параллелепипед

Параллелепипед  — призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого шесть граней и каждая из них —  параллелограмм .

2/18/17

2/18/17

КУБ

Куб  (гексаэдр)— правильный многогранник, каждая грань которого представляет собой квадрат. Частный случай параллелепипеда и призмы.

2/18/17

2/18/17

Пирамида

Пирамида  — многогранник, одна из граней которого (называемая  основанием ) — произвольный многоугольник, а остальные грани (называемые  боковыми гранями ) — треугольники, имеющие общую вершину.

2/18/17

2/18/17

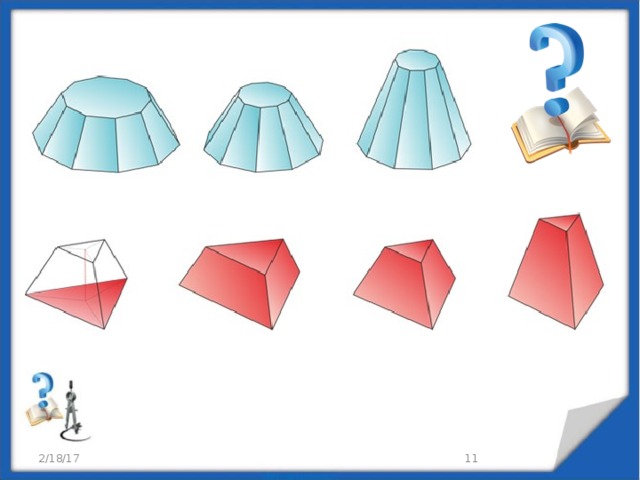
Усеченная пирамида

Усечённая пирамида  — многогранник, образованный пирамидой и её сечением, параллельным основанию.

2/18/17

ТЕЛА ВРАЩЕНИЯ

Тела вращения  — объёмные тела, возникающие при вращении плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости

2/18/17

2/18/17

Шар/Сфера

Шар  — совокупность всех точек пространства, находящихся от центра на расстоянии, не больше заданного.

Сфера  — это геометрическое место точек в пространстве, равноудаленных от некоторой заданной точки ( центра  сферы) или поверхность шара.

Или тело полученное вращением полукруга около его неподвижного диаметра.

2/18/17

2/18/17

Цилиндр

Цилиндр  – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её,

Или тело , полученное в результате вращения прямоугольника вокруг одной из его сторон.

2/18/17

2/18/17

Конус

Конус  – тело, полученное объединением всех лучей, исходящих из одной точки (вершины  конуса ) и проходящих через плоскую поверхность, или

Тело, полученное вращением прямоугольного треугольника вокруг одного из его катетов.

2/18/17

2/18/17

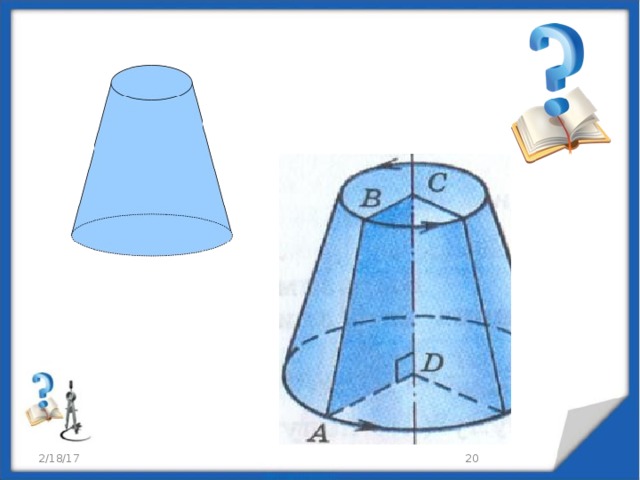
Усеченный конус

Усеченный   конус  – часть  конуса , расположенная между его основанием и секущей плоскостью, параллельной основанию, или

Тело , полученное в результате вращения прямоугольной трапеции вокруг высоты трапеции.

2/18/17

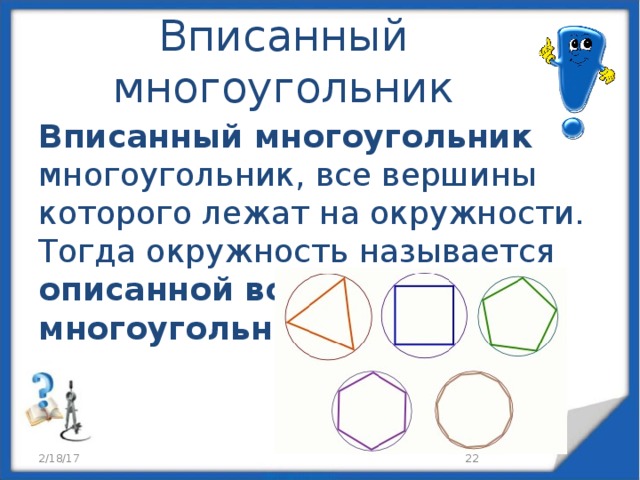
Вписанный многоугольник

Вписанный многоугольник  — многоугольник, все вершины которого лежат на окружности. Тогда окружность называется описанной вокруг многоугольника .

2/18/17

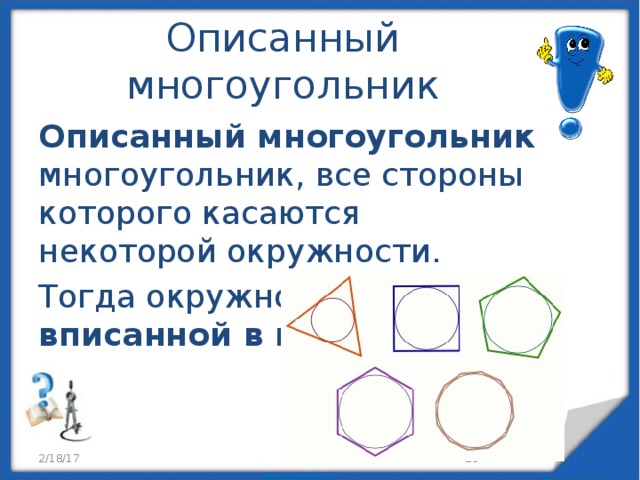
Описанный многоугольник

Описанный многоугольник  — многоугольник, все стороны которого касаются некоторой окружности.

Тогда окружность называется вписанной в многоугольник .

2/18/17

Правила для многоугольников которые можно вписать в окружность и описать окружность вокруг них

Для треугольника всегда возможны и вписанная окружность и описанная окружность.

2/18/17

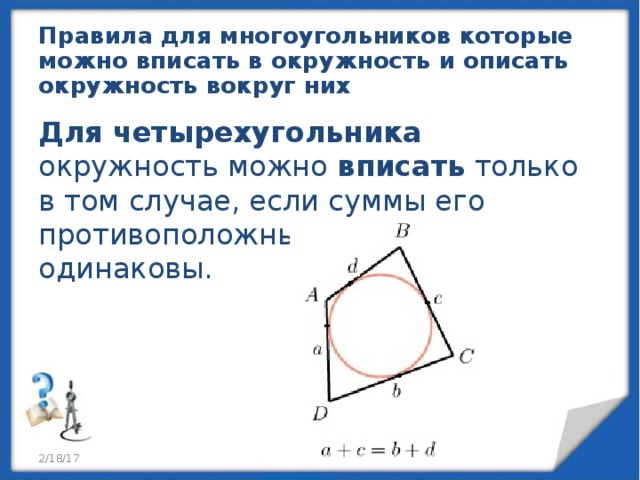
Правила для многоугольников которые можно вписать в окружность и описать окружность вокруг них

Для четырехугольника окружность можно вписать только в том случае, если суммы его противоположных сторон одинаковы.

2/18/17

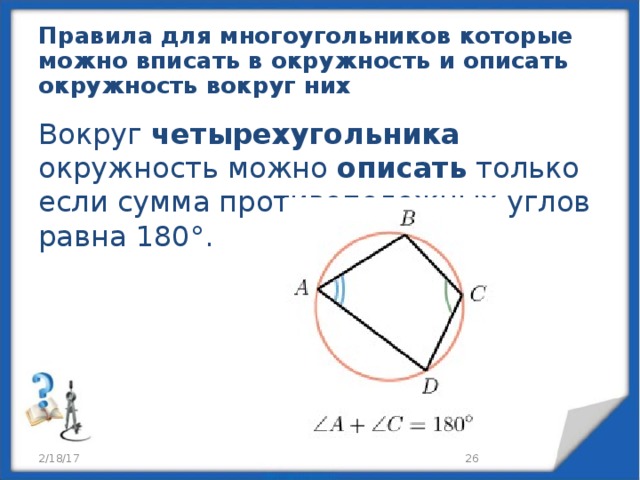
Правила для многоугольников которые можно вписать в окружность и описать окружность вокруг них

Вокруг четырехугольника окружность можно описать только если сумма противоположных углов равна 180°.

2/18/17

Вписанный многогранник

Выпуклый многогранник называется вписанным  , если все его вершины лежат на некоторой сфере.

2/18/17

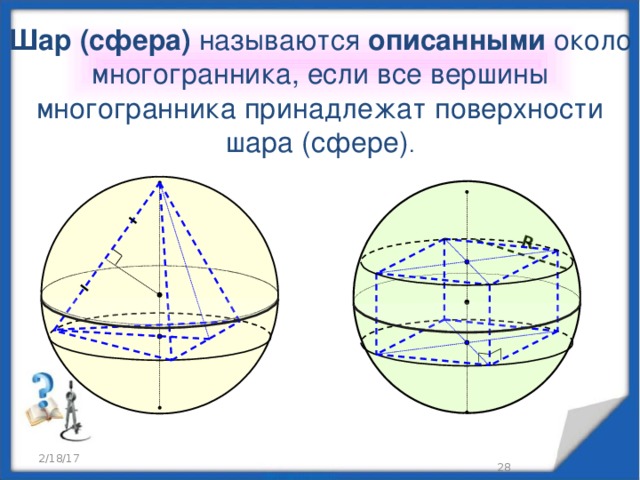
R

Шар (сфера) называются описанными около многогранника, если все вершины многогранника принадлежат поверхности шара (сфере) .

2/18/17

Описанный многогранник

Выпуклый многогранник называется  описанным  , если все его грани касаются некоторой сферы. Эта сфера называется  вписанной  для данного многогранника.

2/18/17

R ш

R ш

R ш

R ц

Шар (сфера) называются вписанными в многогранник, если все грани многогранника касаются поверхности шара (сферы).

2/18/17

30

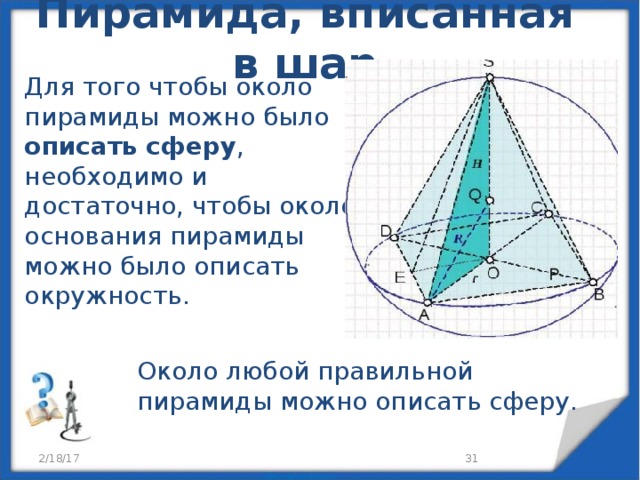
Пирамида, вписанная в шар

Для того чтобы около пирамиды можно было описать сферу , необходимо и достаточно, чтобы около основания пирамиды можно было описать окружность.

Около любой правильной пирамиды можно описать сферу.

2/18/17

30

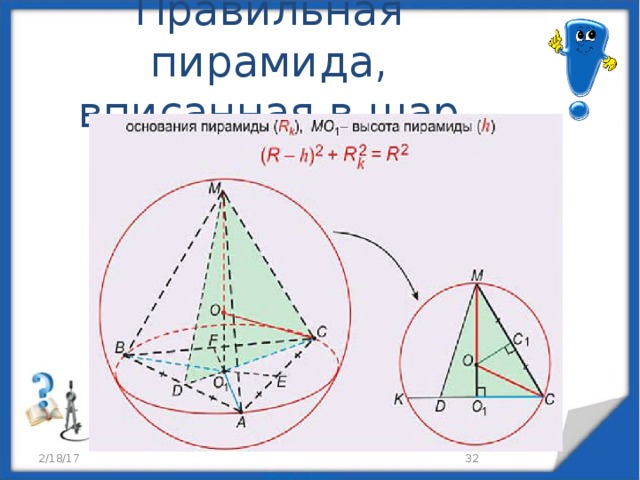
Правильная пирамида, вписанная в шар

2/18/17

30

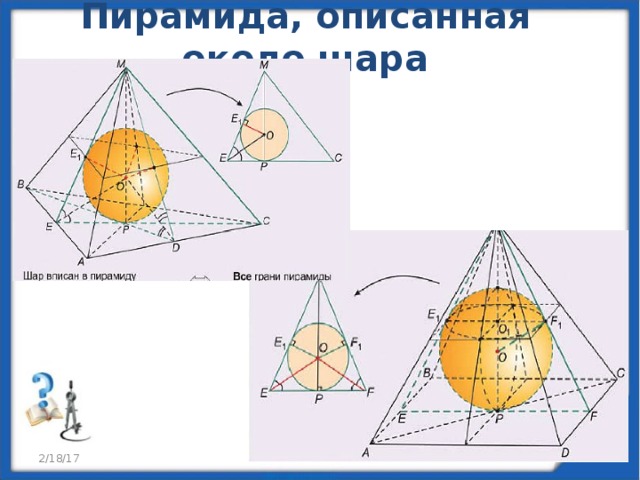
Пирамида, описанная около шара

2/18/17

30

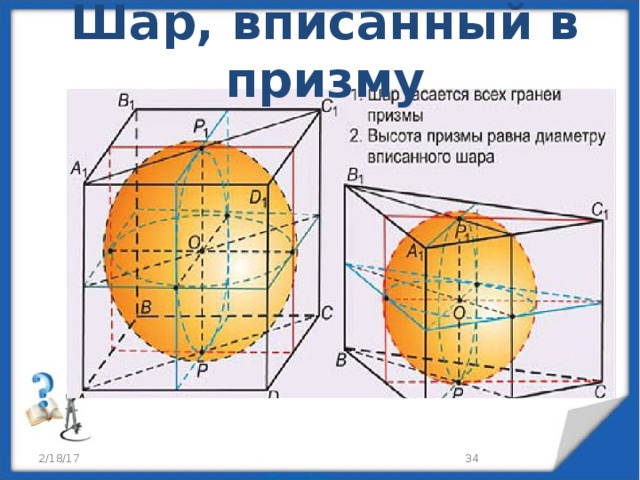
Шар, вписанный в призму

2/18/17

30

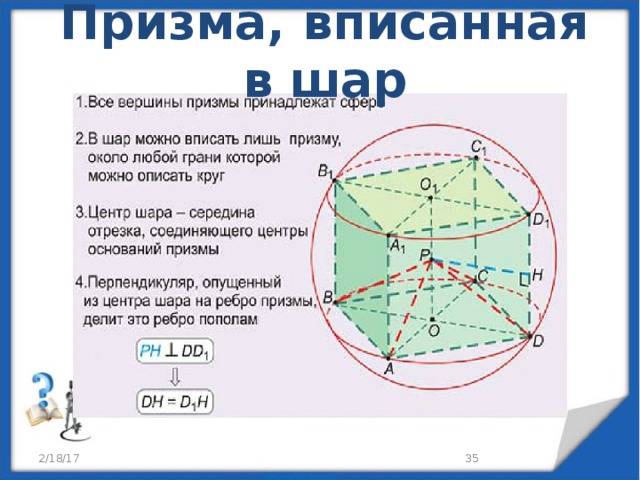
Призма, вписанная в шар

2/18/17

30

R ш

R ш

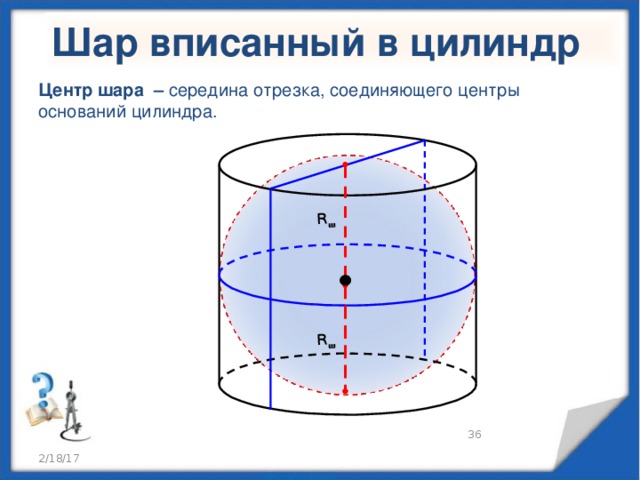
Шар вписанный в цилиндр

Центр шара – середина отрезка, соединяющего центры оснований цилиндра.

30

2/18/17

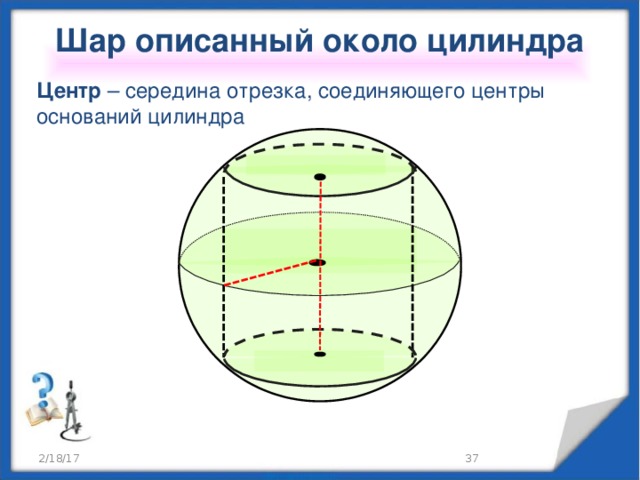
Шар описанный около цилиндра

Центр – середина отрезка, соединяющего центры оснований цилиндра

2/18/17

37

А

А

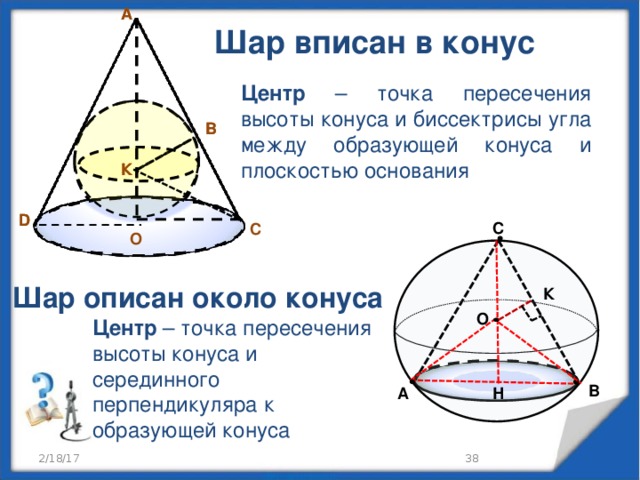
Шар вписан в конус

Центр – точка пересечения высоты конуса и биссектрисы угла между образующей конуса и плоскостью основания

В

В

К

К

D

D

С

С

О

О

Шар описан около конуса

К

О

Центр – точка пересечения высоты конуса и серединного перпендикуляра к образующей конуса

В

Н

А

37

2/18/17

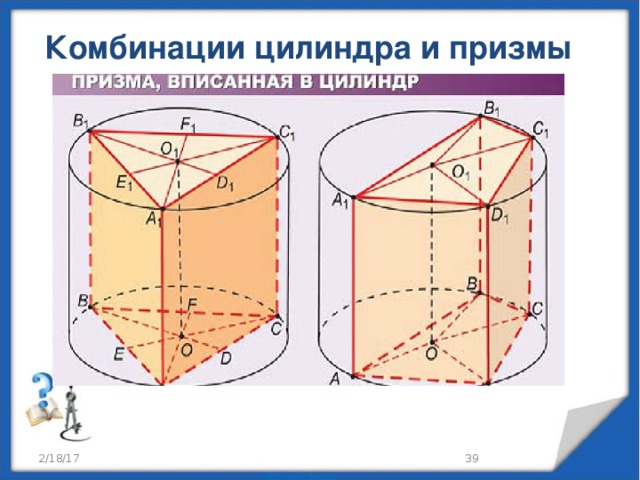
Комбинации цилиндра и призмы

2/18/17

38

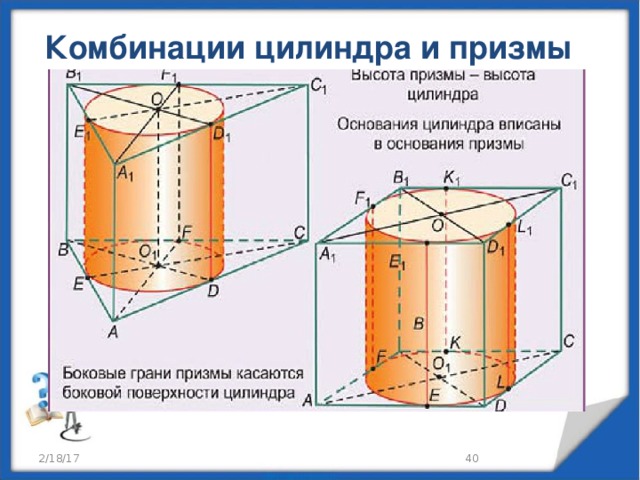
Комбинации цилиндра и призмы

2/18/17

38

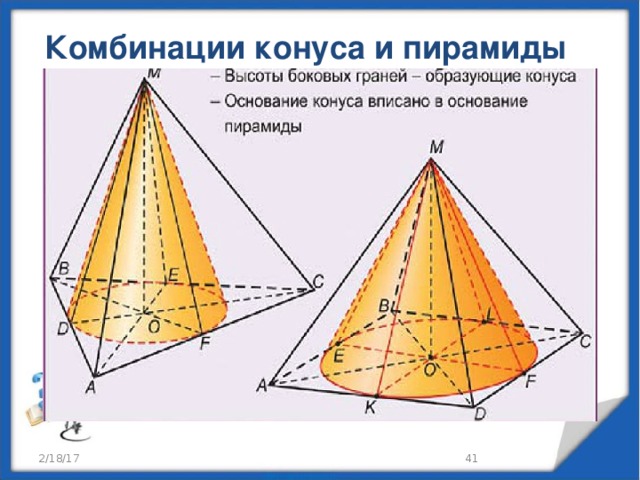
Комбинации конуса и пирамиды

2/18/17

38

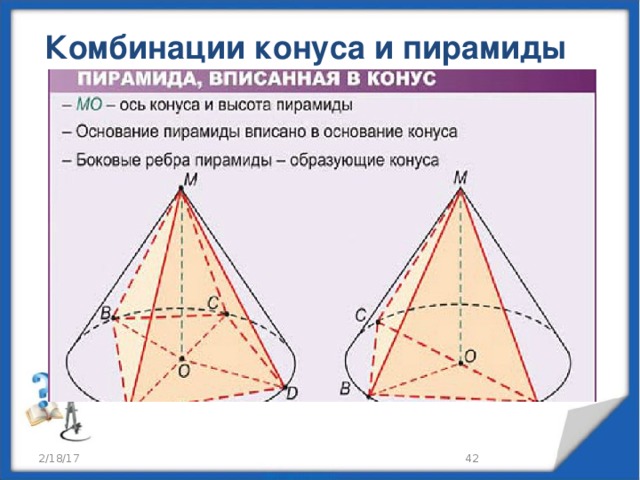
Комбинации конуса и пирамиды

2/18/17

38

2/18/17

38

Изображения комбинаций фигур

2/18/17

38

Изображение сферы

Для большей наглядности изображения сферы в ней выделяют большую окружность - экватор и полюсы.

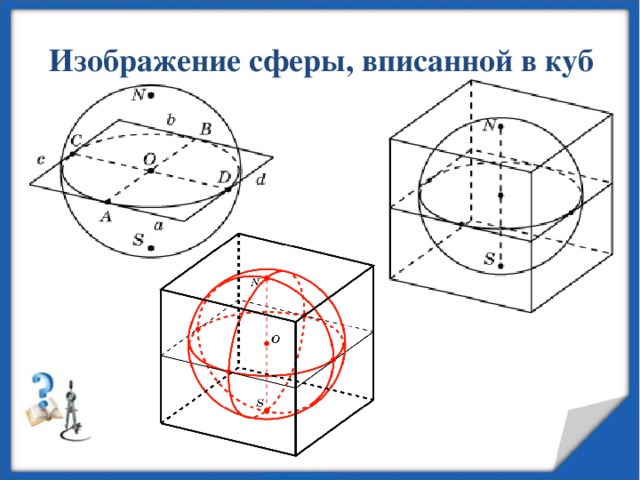
Изображение сферы, вписанной в куб

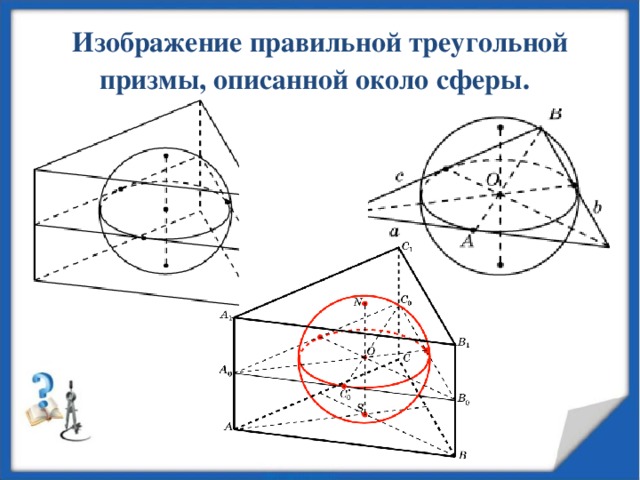
Изображение правильной треугольной призмы, описанной около сферы.

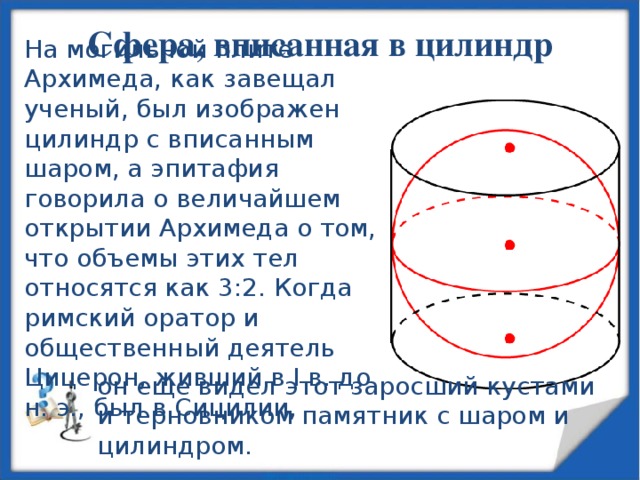
Сфера, вписанная в цилиндр

На могильной плите Архимеда, как завещал ученый, был изображен цилиндр с вписанным шаром, а эпитафия говорила о величайшем открытии Архимеда о том, что объемы этих тел относятся как 3:2. Когда римский оратор и общественный деятель Цицерон, живший в І в. до н. э., был в Сицилии,

он еще видел этот заросший кустами и терновником памятник с шаром и цилиндром.

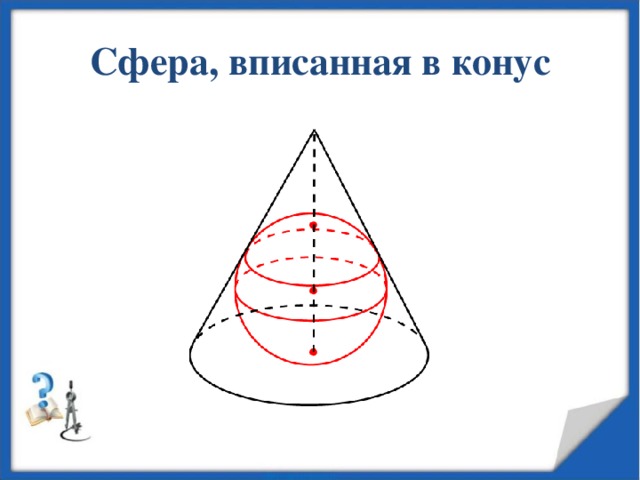
Сфера, вписанная в конус

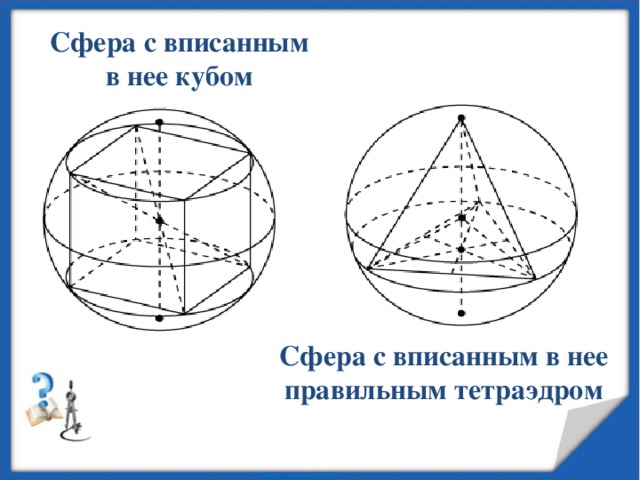
Сфера с вписанным в нее кубом

Сфера с вписанным в нее правильным тетраэдром

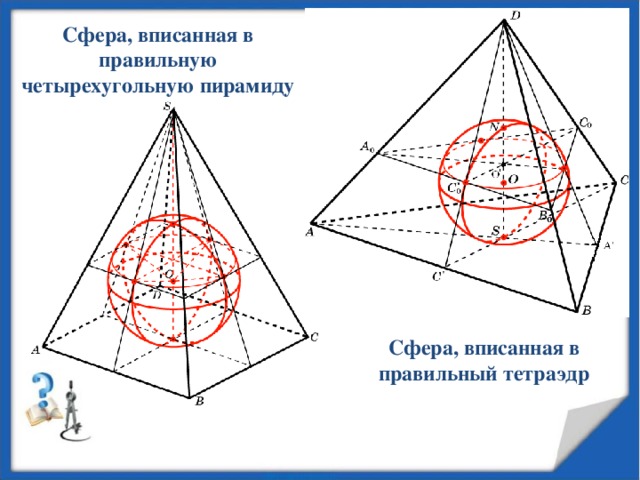
Сфера, вписанная в правильную четырехугольную пирамиду

Сфера, вписанная в правильный тетраэдр

Задачи

38

10

10

Высота конуса 8, образующая 10. Найдите радиус вписанного шара

1

Решение:

А

А

1)

2)

3)

8

8

В

В

4)

К

К

5)

D

С

О

О

2/18/17

38

2

Площадь поверхности шара равна 330.

Найдите площадь полной поверхности цилиндра,

описанного около шара.

Решение:

1)

Н

С

2)

К

О

3)

А

В

4)

2/18/17

54

54

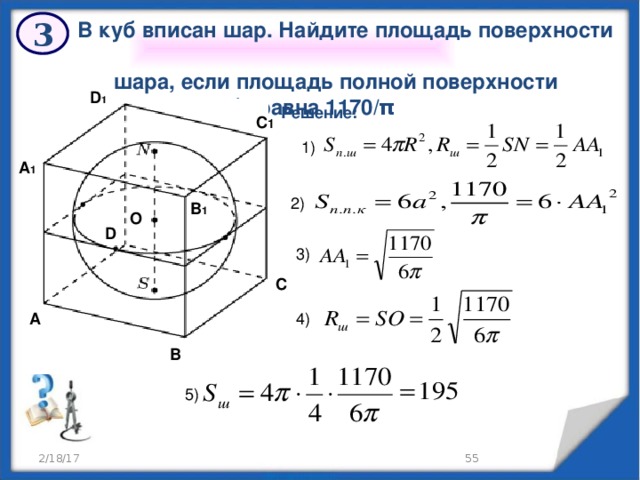
3

В куб вписан шар. Найдите площадь поверхности

шара, если площадь полной поверхности

куба равна 1170/π

D 1

Решение:

С 1

1)

А 1

2)

B 1

О

D

3)

С

4)

А

В

5)

54

2/18/17

54

4

Высота конуса равна 2, образующая равна 4. Найдите радиус описанного шара.

4

С

Решение:

1)

2

2)

О

3)

В

А

Н

4)

5)

54

2/18/17

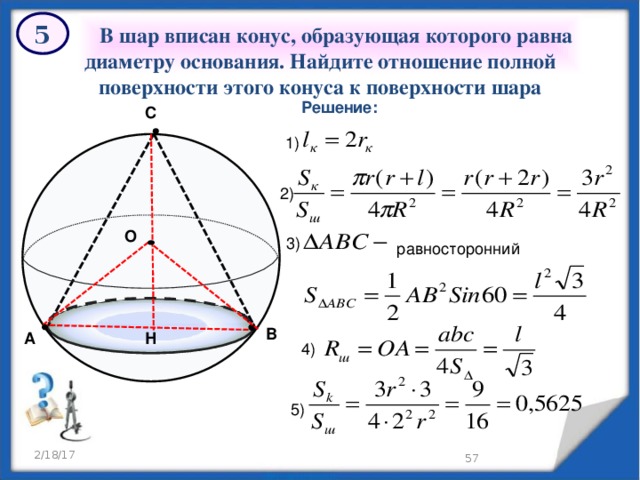
5

В шар вписан конус, образующая которого равна диаметру основания. Найдите отношение полной поверхности этого конуса к поверхности шара

Решение:

С

1)

2)

О

3)

равносторонний

В

А

Н

4)

5)

2/18/17

54

57

Задачи для самостоятельного решения

1В. 1 Найдите площадь поверхности шара, описанного около конуса, у которого радиус основания , а высота равна

Ответ: 25

1В.2 Радиус шара, описанного около куба, равен 3. Найдите площадь поверхности куба.

Ответ:24

2В.2 В шар, площадь поверхности которого равна 100π, вписан цилиндр. Найдите высоту цилиндра, если радиус его основания равен 4.

Ответ: 8

2В.1 В шар вписан конус. Найдите высоту конус, если радиус шара равен 5, а радиус основания конуса равен 4.

Ответ: 6

57

2/18/17

57