Презентация к уроку математики на тему: «Четырёхугольники. Виды четырёхугольников»

Презентация к уроку математики на тему: «Четырёхугольники. Виды четырёхугольников» Презентация предназначена для обучающихся 8 классов (13-14 лет) Работу в ыполнила: Субботина Елена Владимировна, учитель математики МОУ «СОШ № 7 г. Ртищево Саратовской области»

МАТЕМАТИКА - 8 КЛАСС

Четырёхугольник

Дельтоид

Трапеция

Параллелограмм

Ромб

Прямоугольник

Квадрат

ЧЕТЫРЁХУГОЛЬНИК

Четырехугольник  фигура ( многоугольник ), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки. Различают  выпуклые  и невыпуклые четырёхугольники

ПАРАЛЛЕЛОГРАММ

А

В

С

D

5

А

В

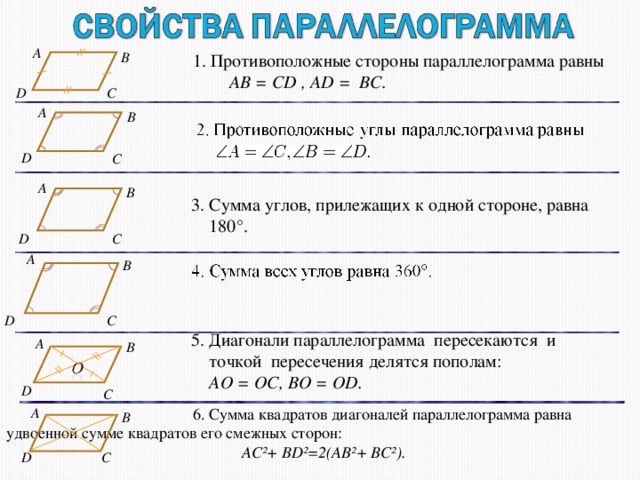
1. Противоположные стороны параллелограмма равны

AB = CD , AD = BC.

• AB = CD , AD = BC.

С

D

А

В

D

С

А

В

3. Сумма углов, прилежащих к одной стороне, равна

180°.

С

D

А

В

С

D

5. Диагонали параллелограмма пересекаются и

точкой пересечения делятся пополам:

AO = OC, BO = OD.

А

В

D

С

А

6. Сумма квадратов диагоналей параллелограмма равна

удвоенной сумме квадратов его смежных сторон:

AC²+ BD²=2(AB²+ BC²).

В

С

D

6

Четырёхугольник ABCD является параллелограммом, если выполняется одно из следующих условий:

В

А

• Две стороны равны и параллельны

AD=BC и AD II BC .

D

С

А

В

2. Противоположные стороны попарно равны

AD=BC и AB=DC .

С

D

А

В

3. Противоположные углы попарно равны:

∠ A = ∠C, ∠B = ∠D.

D

С

А

В

4. Диагонали делятся в точке их пересечения

пополам: AO = OC, BO = OD.

О

D

С

А

В

5. Сумма соседних углов равна 180 градусов:

∠ A + ∠B = 180, ∠B + ∠C = 180,

∠ C + ∠D = 180, ∠D + ∠A = 180.

D

С

7

РОМБ

А

Ромб – параллелограмм,

у которого все стороны равны

AB=BC=CD=DA

D

В

С

8

ПРИЗНАКИ РОМБА

D

D

В

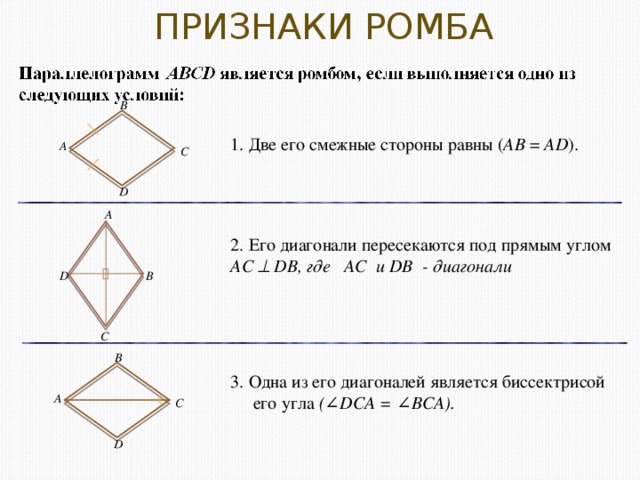
1. Две его смежные стороны равны ( AB = AD ).

А

С

А

2. Его диагонали пересекаются под прямым углом

AC  DB , где AC и DB - диагонали

D

В

С

В

3. Одна из его диагоналей является биссектрисой

его угла (∠DCA = ∠BCA).

А

С

9

ПРЯМОУГОЛЬНИК

Прямоугольник – параллелограмм,

А

В

у которого все углы прямые (равны 90 ˚ )

D

С

10

СВОЙСТВА ПРЯМОУГОЛЬНИКА

• Прямоугольник является параллелограммом,

а поэтому его противоположные стороны

параллельны АВ || CD, AD || ВС.

В

А

С

D

В

2. Диагонали прямоугольника равны

AC=BD и BD=AC .

А

С

D

ПРИЗНАКИ ПРЯМОУГОЛЬНИКА

Параллелограмм является прямоугольником, если выполняются условия:

В

А

1. Диагонали параллелограмма равны

AC=BD , где AC , BD – диагонали.

D

С

А

В

2. Хотя бы один угол прямой.

С

D

11

D

C

B

A

КВАДРАТ –

• прямоугольник, у которого все стороны равны;
• правильный четырёхугольник (все углы и стороны равны)

Квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.

ДЕЛЬТОИД – четырёхугольник, у которого две пары смежных сторон равны.

Дельтоид имеет форму воздушного змея .

B

A

C

D

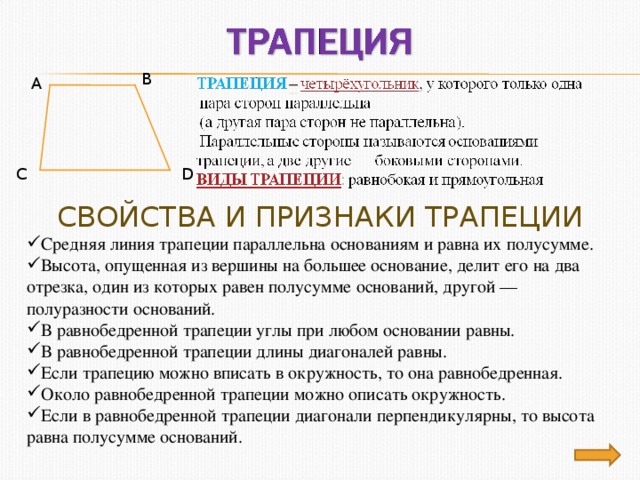
СВОЙСТВА И ПРИЗНАКИ ТРАПЕЦИИ

• Средняя линия трапеции параллельна основаниям и равна их полусумме.
• Высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, другой — полуразности оснований.
• В равнобедренной трапеции углы при любом основании равны.
• В равнобедренной трапеции длины диагоналей равны.
• Если трапецию можно вписать в окружность, то она равнобедренная.
• Около равнобедренной трапеции можно описать окружность.
• Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

• За счёт трёхмерной оптической иллюзии в комнате Эймса (придумал в 1946 году) ребёнок в ближнем углу кажется великаном по сравнению с тем, что стоит в дальнем. На самом деле форма комнаты – трапеция . Эффект усиливается из-за искажённой шахматной клетки.

• Более 100 парашютистов сделали самый большой ромб в мире.

• Чёрный квадрат — самая известная работа Казимира Малевича, созданная в 1915 году. Представляет собой полотно размером 79,5 на 79,5 сантиметров, на котором изображён чёрный квадрат на белом фоне. Малевич писал квадрат тонкой кисточкой, есть версия, что там что-то уже было нарисовано.

• https://ru.wikipedia.org/wiki/ Четырёхугольник
• https://ru.wikipedia.org/wiki/ Воздушный_змей
• https://ru.wikipedia.org/wiki/ Трапеция
• http://flogiston.ru/blog/ames_room комната Эймса
• https://ru.wikipedia.org/wiki/%D7%B8%F0%ED%FB%E9_%EA%E2%E0%E4%F0%E0%F2 чёрный квадрат
• https://ru.wikipedia.org/wiki/%D0%EE%EC%E1 ромб
• Геометрия: учеб. Для 7-9 кл. общеобразовательных учреждений/ А.В. Погорелов- м.: Просвещение, 2013
• Энциклопедия для детей. Математика/ ред. Коллегия М. Аксёнова. - М.: Астрель, 2007