Презентация к уроку математики в 10 классе по теме "Четность функций"

ЧЁТНЫЕ И НЕЧЁТНЫЕ ФУНКЦИИ

Учитель математики

Хаматова С.Н.

10 класс

ПЛАН УРОКА

• Организационный момент.
• Повторение изученного.
• Самостоятельная работа.
• Подготовка к изучению нового материала.
• Изучение новой темы.
• Закрепление изученного материала.
• Проверка усвоения нового материала.
• Подведение итогов урока.
• Домашнее задание

Сформулировать определения

САМОСТОЯТЕЛЬНАЯ РАБОТА

ВАРИАНТ 1

1. Найдите область определения функции:

а) б)

в)

2. Найдите область значений функции:

а)

б)

ВАРИАНТ 2

1. Найдите область определения функции:

а) б)

в)

2. Найдите область значений функции:

а)

б)

ПРОВЕРЬ ОТВЕТЫ

ВАРИАНТ 1

1. Найдите область определения функции:

а)

б)

в)

2. Найдите область значений функции:

а)

б)

ВАРИАНТ 2

1. Найдите область определения функции:

а)

б)

в)

2. Найдите область значений функции:

а)

б)

?Какие промежутки симметричны относительно нуля?

• (-∞;+∞)
• (-10;10)
• (-10;10 ]
• (-∞;-5)(5;+∞)
• (-7;+∞)
• (-∞;+∞) \{-1 ;0;1 }
• (-∞;+∞) \{-1 ;1 }
• (-∞;+∞) \{-1 ;0 }
• (-∞;+∞) \{ 1 }

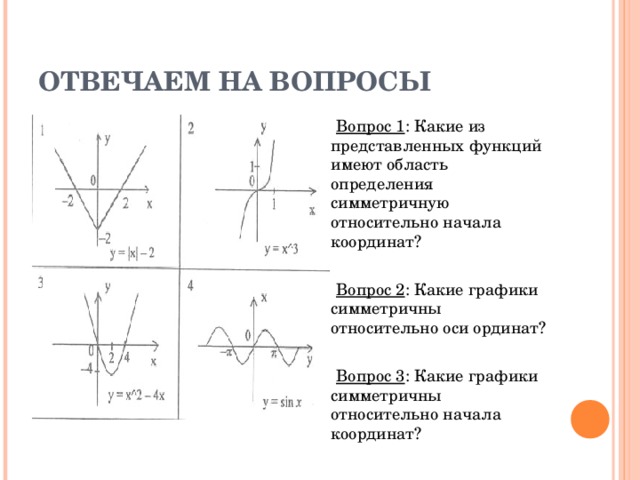
ОТВЕЧАЕМ НА ВОПРОСЫ

Вопрос 1 : Какие из представленных функций имеют область определения симметричную относительно начала координат?

Вопрос 2 : Какие графики симметричны относительно оси ординат?

Вопрос 3 : Какие графики симметричны относительно начала координат?

Изучение нового материала

«Чётные и нечётные

функции»

Функции

Чётные

Нечётные

Ни чётные ни нечётные

ЧЁТНАЯ ФУНКЦИЯ

Функция f ( x ) называется чётной, если она обладает двумя свойствами:

• её область определения симметрична относительно нуля; для любого х из области определения выполняется равенство: f (- x ) = f ( x ).
• её область определения симметрична относительно нуля;
• для любого х из области определения выполняется равенство: f (- x ) = f ( x ).

График чётной функции симметричен относительно оси ординат.

НЕЧЁТНАЯ ФУНКЦИЯ

Функция f ( x ) называется нечётной, если она обладает двумя свойствами:

• её область определения симметрична относительно нуля; для любого х из области определения выполняется равенство: f (- x ) = - f ( x ).
• её область определения симметрична относительно нуля;
• для любого х из области определения выполняется равенство: f (- x ) = - f ( x ).

График нечётной функции симметричен относительно начала координат.

Алгоритм проверки функции на чётность:

• найти D(f) ;
• проверить её на симметрию относительно 0

(если D(f) не симметрична относительно 0, то функция ни чётная ни нечётная);

• подставить в функцию вместо

каждого х (-х) ;

• если f(-x) = f(x) , то функция – чётная;
• если f(-x) = - f(x) , то функция – нечётная;
• в противном случае, функция – ни чётная ни нечётная.

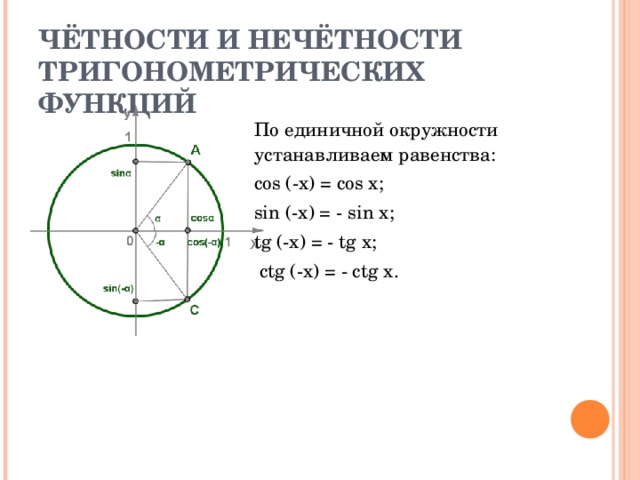
ЧЁТНОСТИ И НЕЧЁТНОСТИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ

По единичной окружности устанавливаем равенства:

cos (-x) = cos x;

sin (-x) = - sin x;

tg (-x) = - tg x;

ctg (-x) = - ctg x .

Функции y = sin x , y = tg x , y = ctg x являются нечётными.

Функция y = cos x является чётной.

КАКИЕ ИЗ ПРЕДСТАВЛЕННЫХ ФУНКЦИЙ ЯВЛЯЮТСЯ ЧЁТНЫМИ, А КАКИЕ НЕЧЁТНЫМИ?

ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА

ПРОВЕРКА УСВОЕННОГО МАТЕРИАЛА

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

13)

14)  

b

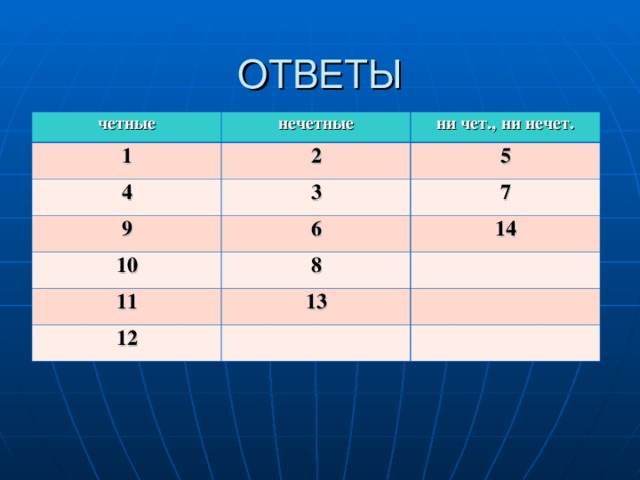
четные

нечетные

1

ни чет., ни нечет.

2

4

3

5

9

10

7

6

8

14

11

13

12

ЧЕТНОСТЬ ФУНКЦИЙ В ЗАДАНИЯХ ЕГЭ

ЧЕТНОСТЬ ФУНКЦИЙ В ЗАДАНИЯХ ЕГЭ

ЧЕТНОСТЬ ФУНКЦИЙ В ЗАДАНИЯХ ЕГЭ

1 вариант

№ 1

2 вариант

4

№ 2

-2

-2

№ 3

2

12

№ 4

3

36

5

• 12-16 «3»
• 17- 21 «4»
• 22- 23 «5»

ДОМАШНЕЕ ЗАДАНИЕ

№ 57 (а, б); №59(а,б)