Россия, Бокситогорск
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 15.06.2025 20:39
Мурзалиева Татьяна Александровна
учитель математики
75 лет
1 805
34 870 
Местоположение
Специализация
Презентация к уроку "Решение неравенств второй степени с одной переменной"
Категория:
Математика
22.10.2016 01:02
Просмотр содержимого документа
«Презентация к уроку "Решение неравенств второй степени с одной переменной"»
Тема: «Решение неравенств второй степени с одной переменной».
9 класс
«С тех пор как существует мирозданье, Такого нет, кто б не нуждался в знанье. Какой мы ни возьмем язык и век, Всегда стремится к знанью человек »
персидско-таджикский поэт Рудаки
+
-
Вопрос 1.
Время на ответ 30 сек.
Ваше время истекло
- Округлите число 23,387 до сотых?
Ответы: А) 23,38
Б) 23,3
В) 23,39
Г) 23,4
Время
Вопрос 2.
Время на ответ 30 сек.
Ваше время истекло
- Из формулы мощности N = выразите время t.
Ответ: ________
Время
Вопрос 3.
Время на ответ 30 сек.
Ваше время истекло
2
- Как величина 506 тыс. км записывается в стандартном виде
Ответы:
А) 5,06*10
Б) 5,06*10
В) 5,06*10
Г) 5,06*10
2
3
4
5
Время
Вопрос 4.
Время на ответ 30 сек.
Ваше время истекло
- Какое из приведенных ниже выражений тождественно равно (х–7)(х-3)?
Ответы: А) (х-7)(3-х) Б) –(х-7)(3-х) В) (7-х)(х-3) Г) –(7-х)(3-х)
Время
Вопрос 5.
Ваше время истекло
Время на ответ 30 сек.
- Решите уравнение:
х - 7х + 6 = 0
2
Ответ: ____________
Время
Вопрос 6.
Время на ответ 30 сек.
Ваше время истекло
- Найдите дискриминант квадратного
уравнения х + 6х – 5 = 0 .
2
Ответы: А) 16 Б) 56 В) 32 Г) 1
Время
Вопрос 7.
Время на ответ 30 сек.
Ваше время истекло
- Найдите значение выражения
Ответы: А) 1 В) -1 Б) 0 Г)
Время
Вопрос 8.
Ваше время истекло
Время на ответ 30 сек.
- Какое число стоит в конце цепочки?
+4 - 10 ·50 :7
?
6,8
Ответы: А) 5 В) Б) Г)
40
Время
0 , 1 корень В) a Г) a0, 2 корня у х Время " width="640"
Вопрос 9.
Ваше время истекло
Время на ответ 30 сек.
- Укажите знак коэффициента а и количество корней уравнения
2
аx + вx + c=0
Ответы: А) а Б) a0 , 1 корень
В) a
Г) a0, 2 корня
у
х
Время
Вопрос 10.
Время на ответ 30 сек.
Ваше время истекло
у
- При каких значениях х
у ?
Ответы: А)
Б)
В)
Г)
1
-3
0
U
х
U
Время
+
-
Правильные ответы
№ вопроса
1
Ответ
В
2
3
Nt
Г
4
5
Б
1;6
6
7
Б
Б
8
9
В
10
А
Б
Оценка
Баллы
Оценка
10
9 - 8
5
5 - 7
4
0 - 4
3
2
Устная работа
Что можно сказать о количестве корней уравнения
ах ² + вх +с =0 и знаке коэффициента а, если график функции у = ах ² + вх +с расположен следующим образом:
0 ах² + вх +с ≥0 ах² + вх +с 0 ах² + вх +с ≤ 0 " width="640"
Назовите промежутки знакопостоянства функции
у = ах² + вх +с, если ее график расположен следующим образом:
ах² + вх +с 0
ах² + вх +с ≥0
ах² + вх +с 0
ах² + вх +с ≤ 0
Решение неравенств второй степени с одной переменной
0 ( ах ² + вх +с ≥0 ), ах ² + вх +с 0 ( ах ² + вх +с ≤ 0), где а ≠ 0, с опорой на сведения о графике квадратичной функции ( направление ветвей параболы, ее расположение относительно оси 0х ). " width="640"
Цель:
Сформировать умения решать неравенства
ах ² + вх +с 0 ( ах ² + вх +с ≥0 ),
ах ² + вх +с 0 ( ах ² + вх +с ≤ 0),
где а ≠ 0, с опорой на сведения о графике квадратичной функции ( направление ветвей параболы, ее расположение относительно оси 0х ).
0 ( ах² + вх +с ≥0 ), ах² + вх +с 0 (ах² + вх +с ≤ 0), где х – переменная, а, в и с – некоторые числа и а ≠ 0, называют неравенствами второй степени с одной переменной. Решение неравенства второй степени с одной переменной можно рассматривать как нахождение промежутков, в которых соответствующая квадратичная функция принимает положительные или отрицательные значения " width="640"
Неравенства вида
ах² + вх +с 0 ( ах² + вх +с ≥0 ),
ах² + вх +с 0 (ах² + вх +с ≤ 0),
где х – переменная, а, в и с – некоторые числа и а ≠ 0, называют неравенствами второй степени с одной переменной.
Решение неравенства второй степени с одной переменной можно рассматривать как нахождение промежутков, в которых соответствующая квадратичная функция принимает положительные
или отрицательные значения
Какие из следующих неравенств являются неравенствами второй степени с одной переменной?
- Какие из следующих неравенств являются неравенствами второй степени с одной переменной?
Квадратные неравенства
0 9 8 7 6 5 4 3 2 1 № 2. х 2 – х – 6 0 о х -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 № 3. х 2 – х – 6 -1 -2 -3 -4 -5 -6 № 4. х 2 – х – 6 0 " width="640"
Решите неравенство
у = х 2 – х – 6
у
№ 1.
х 2 – х – 6 0
9
8
7
6
5
4
3
2
1
№ 2.
х 2 – х – 6 0
о
х
-7 -6 -5 -4 -3 -2 -1
1 2 3 4 5 6 7
№ 3.
х 2 – х – 6
-1
-2
-3
-4
-5
-6
№ 4.
х 2 – х – 6 0
0 ( a x 2 + b x+ c 2. Рассмотрите функцию y= a x 2 + b x+ c 3. Определите направление ветвей параболы. 4. Найдите точки пересечения параболы с осью абсцисс (для них y=0; х 1 и х 2 найдите, решая уравнение a x 2 + b x+ c =0 ) 5. Схематически постройте график функции y= a x 2 + b x+ c 6. Выделите часть параболы, для которой y 0 (y -2 0 " width="640"
Пример решения неравенства
Алгоритм решения неравенств второй степени с одной переменной
5х 2 +9х-2
2.Рассмотрим функцию
y= 5х 2 +9х-2
3. График функции - парабола, ветви направлены вверх.
4. 5х 2 +9х-2=0
х 1 =-2; х 2 =
5.
1. Приведите неравенство к виду
a x 2 + b x+ c 0 ( a x 2 + b x+ c
2. Рассмотрите функцию
y= a x 2 + b x+ c
3. Определите направление ветвей параболы.
4. Найдите точки пересечения параболы с осью абсцисс (для них y=0; х 1 и х 2 найдите, решая уравнение a x 2 + b x+ c =0 )
5. Схематически постройте график функции y= a x 2 + b x+ c
6. Выделите часть параболы, для которой y 0 (y
-2
0
0 ( a x 2 + b x+ c 2. Рассмотрите функцию y= a x 2 + b x+ c 3. Определите направление ветвей 4. Найдите точки пересечения параболы с осью абсцисс (для них y=0; х 1 и х 2 найдите, решая уравнение a x 2 + b x+ c =0 ) 5. Схематически постройте график функции y= a x 2 + b x+ c 6. Выделите часть параболы, для которой y 0 (y7. На оси абсцисс выделите те значения х, для которых y0 (y 0 -2 " width="640"
Алгоритм решения неравенств второй степени с одной переменной
Пример решения неравенства
5х 2 +9х-2
2.Рассмотрим функцию
y= 5х 2 +9х-2
3. Графиком функции является парабола, ветви которой направлены вверх.
4. 5х 2 +9х-2=0
х 1 =-2; х 2 =
5.
1. Приведите неравенство к виду
a x 2 + b x+ c 0 ( a x 2 + b x+ c
2. Рассмотрите функцию
y= a x 2 + b x+ c
3. Определите направление ветвей
4. Найдите точки пересечения параболы с осью абсцисс (для них y=0; х 1 и х 2 найдите, решая уравнение a x 2 + b x+ c =0 )
5. Схематически постройте график функции y= a x 2 + b x+ c
6. Выделите часть параболы, для которой y 0 (y
7. На оси абсцисс выделите те значения х, для которых y0 (y
0
-2
0 ( a x 2 + b x+ c 2. Рассмотрите функцию y= a x 2 + b x+ c 3. Определите направление ветвей 4. Найдите точки пересечения параболы с осью абсцисс (для них y=0; х 1 и х 2 найдите, решая уравнение a x 2 + b x+ c =0 ) 5. Схематически постройте график функции y= a x 2 + b x+ c 6. Выделите часть параболы, для которой y 0 (y7. На оси абсцисс выделите те значения х, для которых y0 (y8. Запишите ответ в виде промежутков 0 -2 " width="640"
Алгоритм решения неравенств второй степени с одной переменной
Пример решения неравенства
5х 2 +9х-2
2.Рассмотрим функцию
y= 5х 2 +9х-2
3. Графиком функции является парабола, ветви которой направлены вверх.
4. 5х 2 +9х-2=0
х 1 =- 2 ; х 2 =
5.
8. х Є (-2; )
1. Приведите неравенство к виду a x 2 + b x+ c 0 ( a x 2 + b x+ c
2. Рассмотрите функцию
y= a x 2 + b x+ c
3. Определите направление ветвей
4. Найдите точки пересечения параболы с осью абсцисс (для них y=0; х 1 и х 2 найдите, решая уравнение a x 2 + b x+ c =0 )
5. Схематически постройте график функции y= a x 2 + b x+ c
6. Выделите часть параболы, для которой y 0 (y
7. На оси абсцисс выделите те значения х, для которых y0 (y
8. Запишите ответ в виде промежутков
0
-2
2
5х + 9х - 2=0
Рассмотрим функцию . График
функции - парабола, ветви направлены вверх, т.к.
Решим уравнение .
Ответ:
Решить неравенство:
-
-
Нет решений
№ 306.
Решите неравенство :
ветви вверх
Ответ:
Найдите множество решений неравенства
или
ветви вниз
Ответ:
- Найдите множество решений неравенства
у
х
0
Ответ:
- При каких значениях t уравнение
не имеет корней
у
2
t
- 64
=
0
2
- 64= 0
t
-8
8
t
t = 8 или t = -8
Ответ:
В таблице 1 найдите верное решение неравенства 1, в таблице 2 - решение неравенства 2:
1.
2.
Таблица 1
Таблица 2
а
в
в
а
d
с
с
d
В таблице 1 найдите верное решение неравенства 1, в таблице 2- решение неравенства 2:
2.
1.
Таблица 1
Таблица 2
в
а
в
а
с
d
d
с
В таблице 2 найдите верное решение неравенства 1, в таблице 3- решение неравенства 2:
2.
1.
Таблица 2
Таблица 3
а
в
в
а
d
с
с
d
![Маленький тест ПОДУМАЙ! Решите неравенство х 2 + 4х 7 6 5 4 3 2 1 ВЕРНО! [-4; 0] 1 ПОДУМАЙ! (-4; 0) 2 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1 -2 -3 -4 -5 -6 -7 3 4 ПОДУМАЙ!](https://fhd.multiurok.ru/d/4/5/d4579d3617b0a275090d00e5742551e1313297c9/img37.jpg)
Маленький тест
ПОДУМАЙ!
Решите неравенство
х 2 + 4х
7
6
5
4
3
2
1
ВЕРНО!
[-4; 0]
1
ПОДУМАЙ!
(-4; 0)
2
-7 -6 -5 -4 -3 -2 -1
1 2 3 4 5 6 7
-1
-2
-3
-4
-5
-6
-7
3
4
ПОДУМАЙ!
![Маленький тест ПОДУМАЙ! Решите неравенство х 2 + 4х 0 7 6 5 4 3 2 1 ВЕРНО! ПОДУМАЙ! 1 [-4; 0] (-4; 0) 2 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1 -2 -3 -4 -5 -6 -7 3 4 ПОДУМАЙ!](https://fhd.multiurok.ru/d/4/5/d4579d3617b0a275090d00e5742551e1313297c9/img38.jpg)
Маленький тест
ПОДУМАЙ!
Решите неравенство
х 2 + 4х 0
7
6
5
4
3
2
1
ВЕРНО!
ПОДУМАЙ!
1
[-4; 0]
(-4; 0)
2
-7 -6 -5 -4 -3 -2 -1
1 2 3 4 5 6 7
-1
-2
-3
-4
-5
-6
-7
3
4
ПОДУМАЙ!
Маленький тест
ПОДУМАЙ!
Решите неравенство
– х 2 + 4х–6 0
7
6
5
4
3
2
1
ПОДУМАЙ!
1
x=2
2
-7 -6 -5 -4 -3 -2 -1
1 2 3 4 5 6 7
-1
-2
-3
-4
-5
-6
-7
3
Нет решений
4
ВЕРНО!
ПОДУМАЙ!
Маленький тест
Решите неравенство
– х 2 + 6х–9
ПОДУМАЙ!
7
6
5
4
3
2
1
ПОДУМАЙ!
x = 3
1
2
-7 -6 -5 -4 -3 -2 -1
1 2 3 4 5 6 7
-1
-2
-3
-4
-5
-6
-7
3
ВЕРНО!
4
ВЕРНО!
Пример 1. Решим неравенство 3 х - 11х – 4 .
2
y
3 x 2 - 11 x –4
2
y = 3 x - 11 x – 4;
Ветви параболы направлены вверх.
3 x 2 - 11 x – 4 = 0;
x
4
-1/3
x € (-∞; -1/3) U (4; +∞).
x € (-1/3; 4).
Ответ: (-∞; -1/3) U (4; +∞).
Ответ: (-1/3; 4).
Пример 2. Решим неравенство
y
x = 4
4
x
Все числа
Все числа кроме 4.
Ответ: все числа.
Ответ: все числа кроме 4.
Пример 3. Решим неравенство
y
D = -7
Уравнение не имеет корней.
x
Решений нет.
х – любое число
Ответ: решений нет.
Ответ: х – любое число.
А
Решите неравенство
ответ
Б
Найдите решение неравенства:
ответ
ответ
Решите неравенство
В
Найдите решение неравенства:
2
ветви вверх
Ответ:
Решите неравенство
у
х
0
3
или
а = - 2 - ветви вниз
Ответ:
0 и ах ² + вх +с 0 поступают следующим образом: Находят дискриминант квадратного трехчлена и выясняют, имеет ли трехчлен корни; Если трехчлен имеет корни , то отмечают их на оси х и через отмеченные точки проводят схематически параболу , ветви которой направлены вверх при а 0 или вниз при а 0 ; если трехчлен не имеет корней, то схематически изображают параболу, расположенную в верхней полуплоскости при а 0 и в нижней при а 0 ; Находят на оси х промежутки , для которых точки параболы расположены выше оси х ( если решают неравенство ах ² + вх +с 0 или ниже оси х (если решают неравенство ах ² + вх +с 0 ). " width="640"
Для решения неравенств вида ах ² + вх +с 0 и ах ² + вх +с 0 поступают следующим образом:
- Находят дискриминант квадратного трехчлена и выясняют, имеет ли трехчлен корни;
- Если трехчлен имеет корни , то отмечают их на оси х и через отмеченные точки проводят схематически параболу , ветви которой направлены вверх при
а 0 или вниз при а 0 ; если трехчлен не имеет корней, то схематически изображают параболу, расположенную в верхней полуплоскости при а 0 и в нижней при а 0 ;
- Находят на оси х промежутки , для которых точки параболы расположены выше оси х ( если решают неравенство ах ² + вх +с 0 или ниже оси х (если решают неравенство ах ² + вх +с 0 ).
X. Рефлексия.
На уроке я работал активно / пассивно
Своей работой на уроке я доволен / не доволен
Урок для меня показался коротким / длинным
За урок я не устал / устал
Моё настроение стало лучше / стало хуже
Материал урока мне был понятен / не понятен
полезен / бесполезен
интересен / скучен
Домашнее задание мне кажется лёгким / трудным
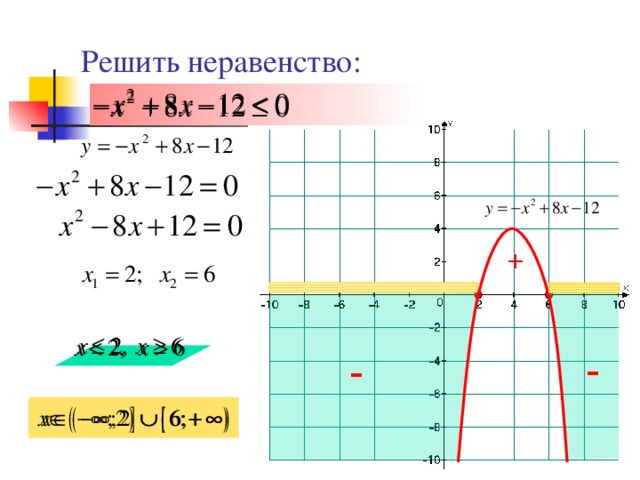
Решить неравенство:
+
-
-
Решить неравенство:
+
+
Нет решений
ЕГЭ. В 10
Камень брошен вертикально вверх. Пока камень не упал, высота, на которой он находится, описывается формулой
h(t)=-5t 2 +18t
(h- высота в метрах,t-время в секундах, прошедшее с момента броска).
Найдите, сколько секунд камень находился на высоте не менее 9 метров.
Для решения необходимо составлять неравенство:
-5t 2 +18t≥9
-5t 2 +18t-9≥0
-5t 2 +18t-9=0
D=324-180=144,
t 1 =(-18+12):(-10) = -6: (-10) = 0,6
t 2 = (-18 – 12) : (-10) = 3
3-0,6=2,4
Ответ: 2,4 с
0 б) 4х - 4х+12 2 " width="640"
Ι вариант
2
2
а) х + х -12 0
ΙΙ вариант.
а) 2х -7х+50 б) 4х - 4х+1
2
2
0 б) 4х 2 -4х+1хЄ(-∞;1)U(2,5;+∞) нет решений " width="640"
Ι вариант. а) х 2 +х-12 0
х Є (-4;3) х Є (-∞;-3)U(-3;+∞)
ΙΙ вариант. а) 2х 2 -7х+50 б) 4х 2 -4х+1
хЄ(-∞;1)U(2,5;+∞) нет решений
Выберите из таблицы 1 графическую интерпретацию для каждого из неравенств 1-4:
1.
2.
3.
Таблица 1
4.
а
в
с
d
e
f
3
4
Выберите из таблицы 1 графическую интерпретацию для каждого из неравенств 1-4:
1.
2.
3.
Таблица 1
4.
а
в
с
d
e
f
4
3
Выберите из таблицы 1 графическую интерпретацию для каждого из неравенств 1-4:
1.
2.
3.
4.
Таблица 1
а
в
с
d
e
f
3
4
Выберите из таблицы 1 графическую интерпретацию для каждого из неравенств 1-4:
1.
2.
3.
Таблица 1
4.
а
в
с
d
e
f
3
4
Выберите из таблицы 1 графическую интерпретацию для каждого из неравенств 1-4:
1.
2.
3.
Таблица 1
4.
а
в
с
d
e
f
3
4
Решаем уравнение:
Находим дискриминант:
- 2 корня
-корней нет
- 1 корень
Находим корни уравнения:
-ветви вверх
(решений нет)
(реш.нет)
(реш.нет)
(решений нет)
-ветви вверх
(решений нет)
(реш.нет)
(реш.нет)
(решений нет)
-ветви вверх
(решений нет)
(реш.нет)
(реш.нет)
(решений нет)
-ветви вниз
(решений нет)
(реш.нет)
(реш.нет)
-ветви вниз
(решений нет)
(реш.нет)
(реш.нет)
-ветви вниз
(решений нет)
(реш.нет)
(реш.нет)
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
