Презентация "Математика на пальцах"

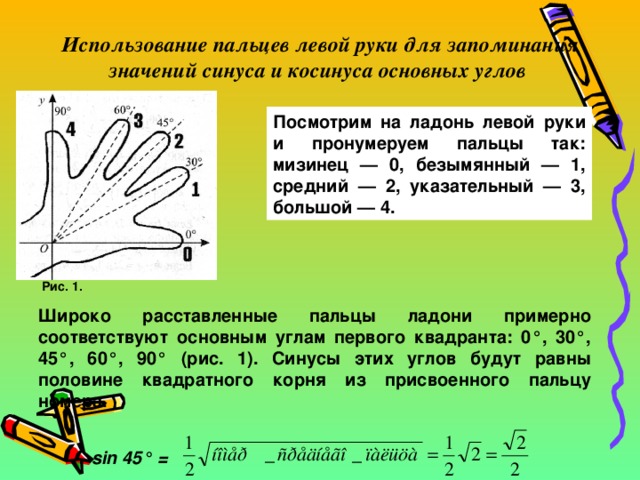
Здравствуйте, уважаемые коллеги!

Разрешите представить Вашему вниманию «Математику на пальцах»

Вам не раз приходилось слышать фразу о том, что математика - страна без границ. Несмотря на свою банальность, она имеет под собой очень веские основания. Позволю утверждать, что математика в жизни человека занимает особое место. Мы настолько срослись с ней, что попросту не замечаем её.

А ведь с математики начинается всё. Ребёнок только родился, а первые цифры в его жизни уже звучат: дата рождения, рост, вес.

Малыш растет, он еще не может выговорить слово "математика", а уже занимается ею, решает небольшие задачи по подсчету игрушек, кубиков. Да и родители о математике не забывают. Готовя ребенку пищу, взвешивая его, решают элементарные задачи: сколько еды нужно приготовить для малыша, учитывая его вес.

Не успели оглянуться, он - уже школьник! Вот здесь и начинаются первые трудности в учебе. Признаемся себе, что у многих самым нелюбимым предметом в школе была математика. И ничего удивительного в этом нет. Мы любим заниматься тем, что у нас получается? Вопрос не риторический. Дело в том, что детишки, которые не в ладах с математикой чаще всего жалуются на то, что они ничего не понимают в этих «дурацких задачах» и этих «длиннющих как удавы» примерах. Сложно полюбить то, чего не понимаешь. Тем не менее, требования для всех учеников школы таковы, что хочешь - не хочешь, любишь - не любишь, а решать, считать, запоминать теоремы все равно придется.

Я работаю учителем математики для того, чтобы научить каждого ученика мыслить, принимать участие в добывании знаний.
Это удивительный мир, в котором, позабыв обо всем на свете, можно решать задачи, доказывать теоремы и получать от этого огромное удовольствие!

Моя задача – помочь ученику сделать первое и самое главное открытие в жизни – открыть свои математические способности.

Как же сформировать у учащихся интерес к математике?

Сделать учебную работу насколько возможно интересной для ребенка и не превратить ее в забаву – это одна из труднейших задач в дидактике (К.Д.Ушинский)

Человеческий мозг, тем более мозг ребенка, не выдерживает однообразия. Чтобы ученик полюбил математику, надо показать всю ее красоту.

 Ещё К.Д. Ушинский писал: «…ученье, лишённое всякого интереса, убивает в ученике охоту к ученью…».

Я стараюсь на уроке похвалить каждого ребенка, сделать все зависящее от меня для того, чтобы у ребенка возникла вера в свои возможности и желание учиться.

Поэтому я не могу допустить, чтобы в глазах моих учеников появилось разочарование. Считаю, что интерес – это ключ к знаниям, и его необходимо поддерживать в детях.

Как заинтересовать математикой? Успех урока целиком зависит от методических приемов, которые выбирает учитель. Как сформировать интерес к предмету у ребенка? Через самостоятельность и активность, через поисковую деятельность на уроке и дома, создание проблемной ситуации, разнообразие методов обучения, через новизну материала, эмоциональную окраску урока.

В своей педагогической работе я стараюсь использовать разнообразные приёмы, которые активизируют учебную деятельность школьников, воспитывают у них активность, самостоятельность мышления, учат применять знания в процессе обучения.

Математика – наука серьезная, чтобы её хорошо освоили ученики вводятся элементы игры. Для любого ребёнка игра – это норма, поэтому в детском возрасте каждый должен играть, даже когда делает серьезное дело. У ребенка есть страсть к игре и её надо удовлетворить

Слабоуспевающий ученик берёт на себя роль «хорошего» ученика в игровых условиях и выполняет её.
Даже самые пассивные из детей включаются в игру с огромным желанием. Они изо всех сил стараются не подвести товарищей.

Какими заданиями можно заинтересовать ученика на уроке математики?

• Числовые ребусы;

• Задачи шутки;

• Числовые построения;

• Текстовые задачи;

• Задачи на разрезание;

• Стихотворения, сказки

• Рисунки, картины из графиков

• Кроссворды, ребусы.

Приведу примеры некоторых упражнений.

1. Подумай и сосчитай:

Чтоб одеть тепло сыночков,

Не хватает двух носочков.

Сколько же в семье сынков,

Если в доме шесть носков? (4)

1. Три курицы за три дня несут три яйца. Сколько яиц снесут 12 таких же курей за 12 дней?

(Одна курица несет одно яйцо за три дня. За 12 дней одна курица снесет четыре яйца, следовательно, 12 курей за 12 дней снесут 12х4=48 яиц)

4. Наблюдательность можно проверить путем счета треугольников.
     Сколько треугольников изображено в геометрической фигуре? ( 35 треугольников)

Незаметно бежит время. И вот уже выпускной класс. Пора сдавать ЕГЭ. Все хотят хорошо сдать ЕГЭ по математике. Тогда просто необходимо уметь считать быстро, правильно и без калькулятора. Ведь главная причина потери баллов на ЕГЭ по математике – вычислительные ошибки.

По правилам проведения ЕГЭ, пользоваться калькулятором на экзамене по математике не разрешено. Главное – внимание, аккуратность и некоторые секретные приемы, о которых я сейчас расскажу. Слайды 5-18

• Три курицы за три дня несут три яйца. Сколько яиц снесут 12 таких же курей за 12 дней?

(Одна курица несет одно яйцо за три дня. За 12 дней одна курица снесет четыре яйца, следовательно, 12 курей за 12 дней снесут 12х4=48 яиц)

Наблюдательность можно проверить путем счета треугольников.

Сколько треугольников изображено на этой геометрической

фигуре?

( 35 треугольников)

• Умножение двухзначных чисел
• Возведение в квадрат двузначных чисел
• Примеры возведения в квадрат двузначных чисел, оканчивающихся на 5
• Умножение двузначного числа на 11
• Извлечение квадратного корня
• Извлечение кубического корня
• Использование пальцев левой руки для запоминания значений синуса и косинуса основных углов

• Пояснения:

1

3

1) 2·6 = 12; два пишем и один запоминаем;

32 . 46=

14

2.

7

+

2) 2·4 = 8; 3·6 = 18; 8 + 18=26; 26 + 1 =27 (десятков); семь пишем и два запоминаем;

2

a b·cd = (10 a + b)·(10c + d) = 100 a c + 10bc + 10 a d + bd = 100 a c + 10(bc + a d) + bd

3) 3·4 = 12; 12 + 2 = 14 (сотен); записываем 14.

36 . 98 =

3

1

+

2

2

8

3 5

ПРАВИЛО

ПРАВИЛО

1

3

• Пояснения:

1)  3 2 =9 ; 2)  (4 . 3) . 2=24 , четыре пишем и два запоминаем;

3) 4 . 4 = 16;

16 + 2 = 18 

43 . 43= 1849

+

2

( a b ) 2 = (10 a + b) 2 = 100 a 2 + 20 a b+ b 2 =

100 a 2 + 10( 2 b a ) + b 2

Возведение в квадрат двузначных чисел

Д ля возведения двузначного числа в квадрат нужно к этому двузначному числу прибавить количество единиц этого числа и полученную сумму умножить на 10 и на цифру десятков числа, а к полученному произведению прибавить квадрат единиц числа.

Другой способ возведения в квадрат задается формулой:

а 2 =а 2 - b 2 + b 2 =(а + b )(а- b ) + b 2 .

Пример 20. Найти квадрат числа 12.

12 2 =(12 + 2)10 • 1 + 2 2 =144 или

12 2 =(12-2)(12+2) + 2 2 =144.

Пример 21. Найти квадрат числа 29.

29 2 =(29 + 9)10 • 2 + 9 2 =841 или

29 2 = (29 + 9)(29 - 9) + 9 2 = 841.

3

1

29 . 29

+

2

8

4

1

ПРАВИЛО

примеры

(10 a + 5) 2 =

= 100 a 2 + 100 a + 25 =

= 100 a ( a + 1) + 25.

a ( a + 1)  — число сотен искомого квадрата; 25 — две последние цифры.

35 2 = 1225 (3 . 4 = 12)

95 2 = 9025

(9 . 10 = 90)

6 5 2 =

( 6 . 7 = 42 )

4 2

2 5

ПРАВИЛО

Умножение двузначного числа на 11

Рассмотрим случай умножения двузначного числа на 11.

Поскольку а b •11=(10 а+ b )(10+1)=100 а +10( а+ b )+ b ,

то ab •11 = a ( a + b ) b , где а — цифра сотен, (а + b ) — цифра десятков, b — цифра единиц.

Пример . Найти произведение 71•11.

Поскольку 7+1 = 8, то цифру 8 запишем между цифрами 7 и 1. Получим 781.

Пример . Найти произведение 79 • 11.

Поскольку 7 + 9=16, цифру 7 увеличим на 1 и получим 8. Между 8 и 9 запишем 6. В итоге получается 869.

Извлечение квадратного корня из полных квадратов

1 2 = 1; 9 2 = 81;

2 2 = 4; 8 2 = 64;

3 2 = 9; 7 2 = 49;

4 2 = 16; 6 2 = 36.

5 2 = 25.

Итак, полный квадрат может оканчиваться только цифрами: 1; 4; 9; 6 ; 5

Пример . 

1) 72 = 49 5329,

следовательно, из тройки и семерки на конце берем 3.

Извлечение кубического корня

1 3 = 1

4 3 =6 4

5 3 =12 5

6 3 =21 6

9 3 =72 9

1 3 = 1

4 3 =6 4

5 3 =12 5

6 3 =21 6

9 3 =72 9

Значит, кубический корень из числа, на конце которого 8, 7, 3, 2, имеет число единиц, дополняющее эти цифры до 10, т. е. 2, 3, 7, 8.

Значит, кубический корень из числа, на конце которого 1, 4, 5, 6, 9 имеет число единиц также 1, 4, 5, 6, 9.

примеры

(27

( 125

(343

Использование пальцев левой руки для запоминания значений синуса и косинуса основных углов

Посмотрим на ладонь левой руки и пронумеруем пальцы так: мизинец — 0, безымянный — 1, средний — 2, указательный — 3, большой — 4.

  Рис. 1.

Широко расставленные пальцы ладони примерно соответствуют основным углам первого квадранта: 0°, 30°, 45°, 60°, 90° (рис. 1). Синусы этих углов будут равны половине квадратного корня из присвоенного пальцу номера.

sin 45° =

Значения косинуса находятся аналогично, только пальцы нужно пронумеровать в обратном порядке: большой — 0, указательный — 1, средний — 2, безымянный 3, мизинец –4 (рис. 2)

Рис.2

cos 30º=.

Математика - интересная наука!

Математику, друзья,

Не любить не как нельзя.

Очень строгая наука,

Очень точная наука

Интересная наука-

Это математика.