Презентация " Наибольшее и наименьшее значение функции на отрезке"

f min (x) = f (a) .

f max (x) = f (b) ;

[a ; b]

[a ; b]

Вывод:

Если функция, непрерывная на [a ; b] ,

является монотонной

на этом отрезке,

то своё наибольшее и наименьшее значение она принимает в концах этого отрезка.

у

а)

а

b

0

f max (x) = f ( а ) ;

[a ; b]

б)

f min (x) = f (a) .

[a ; b]

b

0

Рассмотрим функцию y=f(x) , непрерывную на некотором отрезке [a ; b]

в)

f (Xmax)

Функция у= f(x) немонотонная .

Х 0 = X max

f min (x) = f (b) .

f max (x) = f (Xmax) ;

[a ; b]

[a ; b]

0

а

b

Х 0

Функция у= f(x) немонотонная .

Х0 = X min

г)

f min (x) = f ( X min ).

f max (x) = f (b) ;

[a ; b]

[a ; b]

f(b)

Вывод:

Если функция немонотонная на отрезке, то она может достигать своего наибольшего или наименьшего значения в точках экстремума, принадлежащих данному отрезку.

Х 0

0

a

b

f(Xmin)

д)

Функция у= f(x) немонотонная .

X 0= Xmax

X 1= Xmin

f(X 0 )

f min (x) = f (a) .

f max (x) = f (b) ;

[a ; b]

[a ; b]

а

X 1

0

b

X 0

f(X 1 )

Функция у= f(x) немонотонная .

f(b)

X 0 =Xmin

f min (x) = f (X 0 ) ;

[a ; b]

X 1 =Xmax

f max (x) = f (b) .

X 2 =Xmin

[a ; b]

X 0

a

b

X 2

X 1

0

f(X 0 )

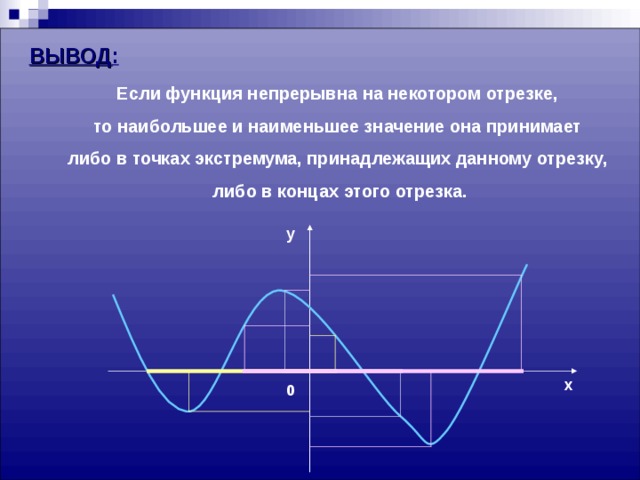
ВЫВОД :

Если функция непрерывна на некотором отрезке,

то наибольшее и наименьшее значение она принимает

либо в точках экстремума, принадлежащих данному отрезку,

либо в концах этого отрезка.

у

х

0

Алгоритм нахождения наибольшего и наименьшего значений функции на отрезке.

1.Выяснить, является ли данная функция непрерывной на данном отрезке.

2.Найти критические точки функции.

3.Выбрать те критические точки, которые принадлежат данному отрезку.

4.Найти значения функции в критических точках (из п.3)

5.Найти значения функции в концах данного отрезка.

6.Выбрать из полученных в п.4 и п.5 значений наибольшее и наименьшее.

7. Записать ответ.