Презентация. Основные свойства фигур

Немного истории

В переводе с греческого слово « геометрия» означает « землемерие». За несколько столетий до н.э в Вавилоне, Египте, Китае и Греции существовали простейшие геометрические знания в основном добываемые практическим путём, они не были собраны в единую систему и передавались от поколения к поколению в виде правил, рецептов, не представляя собой научной теории.

Первым кто начал получать геометрические факты при помощи рассуждений (доказательств), был древнегреческий математик ФАЛЕС, живший в VI в.до н.э.

Постепенно геометрия становилась наукой, в которой большинство фактов устанавливалось путём выводов, рассуждений, доказательств. Систематизация знаний началась с V в.до н.э. Наибольшее влияние на развитие геометрии оказали труды греческого ученого ЕВКЛИДА, жившего в Александрии в III в до н.э Сочинения Евклида руководство по математике «НАЧАЛА» почти 2000 лет служило основной книгой, по которой изучали геометрию В книге была система геометрических сведений, и геометрия впервые предстала, как математическая наука. В геометрии изучали формы, размеры, взаимное расположение предметов и т. д.

Геометрия – это наука о свойствах геометрических фигур

окружность

квадрат

цилиндр

Планиметрия –

Стереометрия

треугольник

куб

параллелограмм

трапеция

многоугольник

• Точка и прямая
• Отрезок
• Полуплоскость
• Полупрямая
• Угол
• Откладывание углов и отрезков
• Треугольник

Точка и прямая – основные геометрические фигуры

B

A

A

a

• a , AB - прямая

• A - точка

Основные свойства

• Какова бы ни была прямая, существуют точки , принадлежащие этой прямой, и точки, не принадлежащие ей.

Через любые две точки можно провести прямую, и только одну

Отрезок

Отрезок – это часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными её точками

A

• «отрезок AB »

B

Основные свойства

• Из трёх точек на прямой одна и только одна лежит между двумя другими.
• Каждый отрезок имеет определённую длину, большую нуля.

Длина отрезка равна сумме длин частей, на которые он разбивает любой его точкой.

A

AC + CB = AB

C

B

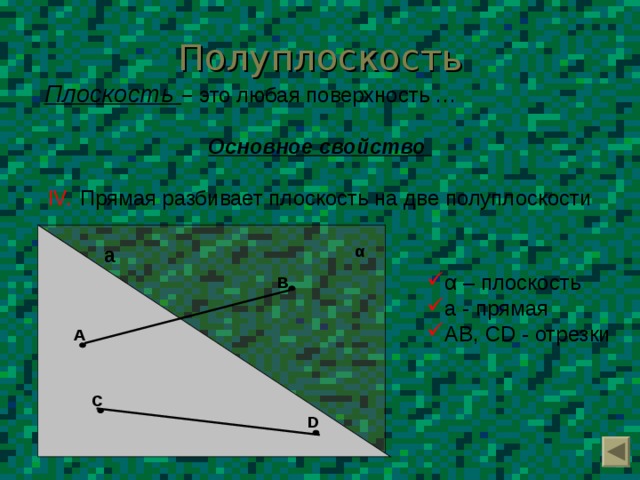
Полуплоскость

Плоскость – это любая поверхность …

Основное свойство

• Прямая разбивает плоскость на две полуплоскости

a

α

• α – плоскость
• a - прямая
• AB , CD - отрезки

B

A

C

D

Полупрямая луч это часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной её точки.

B

• «луч AB и луч a »

A

a

Дополнительные полупрямые это различные полупрямые одной и той же прямой, имеющие общую начальную точку.

O

A

B

Лучи AO и OB – дополнительные лучи

Угол

Угол – это фигура, которая состоит из точки – вершины угла – и двух различных полупрямых, исходящих из этой точки, - сторон угла.

a

• «угол AOB » -
• «угол ab » -

A

O

b

B

Основное свойство

• Каждый угол имеет определённую градусную меру, большую нуля. Развёрнутый угол равен 180 0 . Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.

c

a

b

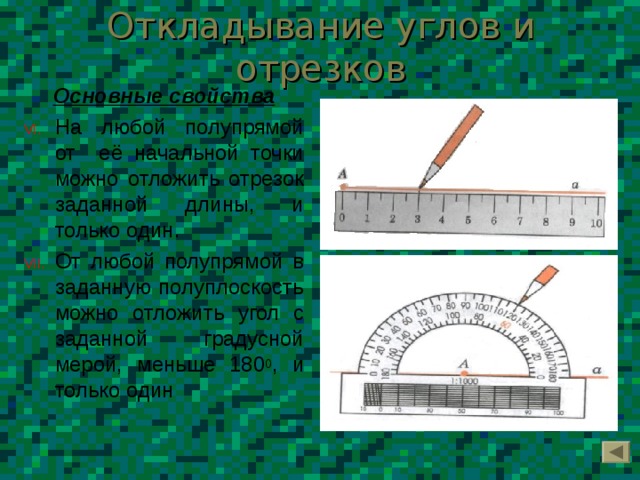
Откладывание углов и отрезков

Основные свойства

• На любой полупрямой от её начальной точки можно отложить отрезок заданной длины, и только один.
• От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньше 180 0 , и только один

Треугольник фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки – сторонами.

B

• A , B , C – вершины
• AB , BC , AC – стороны
• углы

A

C

Основное свойство

• Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой

B 1

B

• ∆ ABC = ∆ A 1 B 1 C 1

A

C

C 1

A 1

a

Параллельные прямые – прямые, которые не пересекаются

• a ║b – «прямая a параллельна прямой b »

a

b

Основное свойство

• Через точку не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.

• a , b – прямые, А – точка не лежит на прямой a
• b є A
• a║b

a

A

b