Россия, Махачкала
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Вам необходимо войти на сайт или зарегистрироваться
Была в сети 20.04.2021 16:44
Алиева Эльмира Асхабовна
учитель математики и информатики
54 года
2 285
27 295 
Местоположение
Специализация
Презентация по математике "Построение графика квадратичной функции, содержащий модуль."
Категория:
Математика
23.08.2017 14:34
Просмотр содержимого документа
«Презентация по математике "Построение графика квадратичной функции, содержащий модуль."»
«Учиться можно только весело.
Чтобы переварить знания, надо поглощать их с аппетитом».
Анатоль Франс
10.2014год
Тема урока:
«Построение графика квадратичной функции, содержащий модуль»
«Быть сильным хорошо, быть умным лучше вдвое»
Математика-
царица
Всех наук
Цели урока:
- Образовательные:
повторение пройденного материала, закрепить навыки по построению графика квадратичной функции
научиться строить графики кв.функции, содержащие модуль.
- Развивающие: развивать логическое мышление, алгоритмическую культуру, внимание, навыки самостоятельной работы с источником информации и самоконтроля, поддерживать интерес к математике.
- Воспитательные: воспитывать последовательность, ответственность, самостоятельность, настойчивость, дисциплинированность.
ГЛАВНАЯ
ВЫХОД
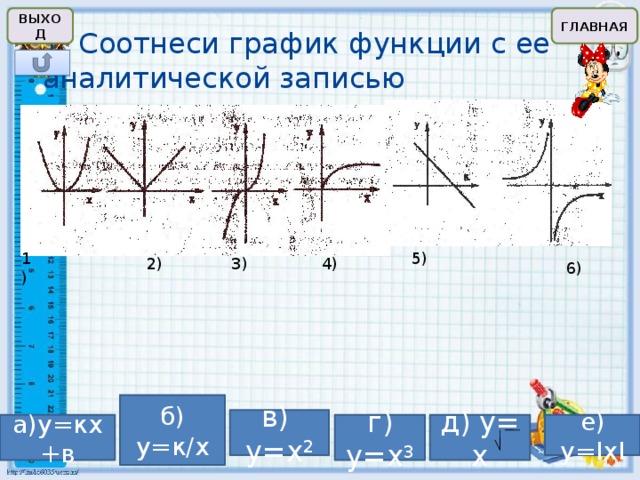
1. Соотнеси график функции с ее аналитической записью
5)
1)
3)
4)
2)
6)
б) у=к/х
в) у=х 2
д) у= х
а)у=кх+в
г) у=х 3
е) y=IxI
Давайте узнаем следующие графики функций :
“ В меня поэты влюблены, Буквально все восхищены. Литературный я прием И график функции притом”.
Гипербола
1. Какова ее область определения? область значений?
2. Как располагаются ветви гиперболы в зависимости от знака числа к?
0 " width="640"
y = k / x
k
y = k / x
k 0
Угадайте следующий график.
“ А я бесхитростна, проста – Такой характер у меня. Смеются надо мной друзья: Мол, нет извилин у меня. Но я с дороги не сверну, Ведь жить иначе не могу”.
Прямая
1. Назовите общее уравнение прямой.
2. Графиком какой функции является прямая?
3. Что такое прямая пропорциональность?
0 k " width="640"
k 0
k
Алгебраическое определение модуля
|a| =
Сократить дробь:
График любой квадратичной
функции – парабола.
Квадратичная функция
Квадратичной функцией называют функцию, которую можно задать формулой вида
y = a x 2 + b x + c , где a , b и с - некоторые числа, причём а ≠ 0.
Падение баскетбольного мяча
Вращающийся сосуд с жидкостью
Параболический фонтан
Библиотека с крышей в форме параболы в норвегии
Укажите алгоритм построения графиков функций:
Построение графика функции
y=(x-4) 2 -8.
17
y=x 2
y=x 2 .
y=(x-4) 2
y=(x-4) 2_ 8
I этап.
Построение
параболы
y
.
.
.
.
.
II этап.
Сдвиг вдоль
оси абсцисс
на 4 единицы
вправо.
.
.
.
.
1
x
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0
1
.
4
III этап.
Сдвиг вдоль
оси ординат
на 8 единиц
вниз.
.
.
.
.
.
.
-8
17
18
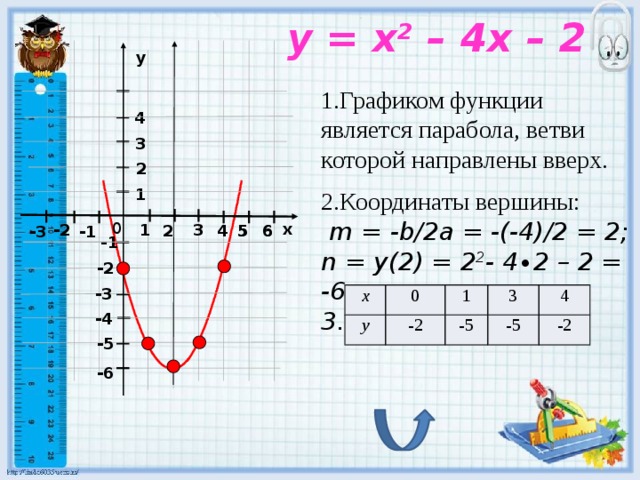
y = x 2 – 4x – 2
y
1.Графиком функции является парабола, ветви которой направлены вверх.
2.Координаты вершины:
m = -b/2a = -(-4)/2 = 2;
n = y(2) = 2 2 - 4∙2 – 2 = -6
3.
4
3
2
1
0
x
-2
1
3
4
4
6
5
5
6
2
-1
-3
-1
-2
-3
х
у
0
-2
1
-5
3
-5
4
-2
-4
-5
-6
Древняя китайская мудрость Скажи мне - и я забуду, Покажи мне - и я запомню, Вовлеки меня – и я пойму
Практическая работа. Построить графики функций:
- 1группа
- 2группа
- 3группа
- 4группа
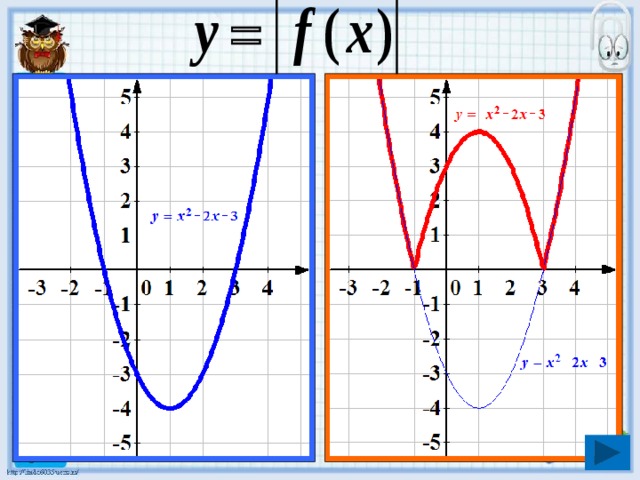
Построение графика функции
1. Построить график функции
2 .Часть графика, где т.е в верхней полуплоскости, оставить без изменения .
3 .Часть графика, которая
расположена в нижней
полуплоскости, отобразить
симметрично относительно оси абсцисс.
Построение графика функции
1 .Построить график функции
2. Часть графика при ,
т.е в правой полуплоскости, оставить без изменения и отобразить симметрично относительно ОУ
Функция и живопись,
что между ними общего?
The Code of Da Vinchi
у
0
Найти наибольшее целое значение «а», при котором уравнение имеет более двух корней?
Решение:
Если а = 1, то 3 корня
Если 1
Если то боле 2 корней.
Наибольшее целое а=2.
Ответ : а=2
Домашнее задание:
№ 107,110.
В тетрадях записать полученные на уроке выводы
Спасибо за работу!
Оцените своё настроение и состояние после проведённого урока. (выберите левой кнопкой мыши соответствующее изображение )
?
Выход
Выход
Выход
Выход
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
