Презентация по теме: "Логика"

ПОДУМАЙ И ОТВЕТЬ…

• Чтобы проползти по беговой дорожке одного стадиона по часовой стрелке, улитке потребуется полтора часа. Когда улитка ползет по той же дорожке против часовой стрелке, то полный круг она совершает за 90 минут. Чем объяснить несовпадение результатов?
• Поезд отправляется из Бостона в Нью-Йорк. Через час другой поезд отправляется из Нью-Йорка в Бостон. Оба поезда едут с одинаковой скоростью. Какой из них в момент встречи будет находиться на меньшем расстоянии от Бостона?

Клокова Е.Е.

Разгадайте ребус

Клокова Е.Е.

Алгебра логики

• Урок № 1
• Урок № 2

Выход

Клокова Е.Е.

Историческая справка

В 1842 году английский математик Джордж Буль разработал математическую логику или алгебру логики, которую впоследствии стали называть «булевой алгеброй». В булевой алгебре высказывания принято обозначать прописными латинскими Буквами: А,В, X,Y . В алгебре Буля введены три основные логические операции с высказываниями: сложение, умножение, отрицание .

Определены аксиомы (законы) алгебры логики для выполнения этих операций. Действия, которые производятся над высказываниями, записываются в виде логических выражений.

Спустя 100 лет алгебра логики стала основой теории цифровых вычислительных машин, ее используют в компьютерной логике, электронике, в основе всех микропроцессорных операций.

Джордж Буль

2 .11.1815г. - 8.12.1864г.

Клокова Е.Е.

ЛОГИКА - ЭТО

наука, изучающая мышление как средство познания объективного мира.

Основные формы мышления:

• Понятие
• Суждение
• Умозаключение

Клокова Е.Е.

ПОНЯТИЕ - это

форма мышления, в которой отражаются существенные признаки отдельного предмета или класса однородных предметов

Например : класс МЕБЕЛЬ – к ней относятся предметы однородные по своему составу

Клокова Е.Е.

СУЖДЕНИЕ - это

мысль, в которой что-либо утверждается или отвергается о предметах.

Например : Весна наступила, и грачи прилетели.

Клокова Е.Е.

Умозаключение - это

прием мышления, посредством которого из исходного знания получается новое знание.

Например :

Все металлы – простые вещества.

Литий – металл.

Литий – простое вещество .

Клокова Е.Е.

Иначе называют…

• Алгебра логики
• Алгебра высказываний
• Математическая логика
• Булева алгебра

Суждение – это высказывание, т.е. повествовательное предложение, о котором можно сказать истинно или ложно.

Клокова Е.Е.

НАПРИМЕР:

• Земля – планета солнечное системы
• 2+8
• Всякий квадрат есть параллелограмм
• Каждый параллелограмм есть квадрат
• 2*2=5

Это всё высказывания, то есть суждения. Простое высказывание в алгебре логики называется логической переменной и обозначается латинской буквой (например: А, В, С и т.д.).

Клокова Е.Е.

Но…

• Уходя, гасите свет.
• Да здравствует мыло душистое и полотенце пушистое.

Повествовательные предложения, о которых нельзя сказать истинны они или ложны, не являются высказываниями.

Клокова Е.Е.

Сложные высказывания.

Сложные высказывания получают путем объединения простых высказываний связками – союзами И, ИЛИ и частицей НЕ .

Значение истинности сложных высказываний зависит от истинности входящих в них простых высказываний.

Клокова Е.Е.

Составьте сложное высказывание

• На улице идет дождь.
• На улице идет снег.
• На улице пасмурно.
• На улице светит солнце.

В первом случае оно должно быть всегда истинным, а во втором – всегда ложным .

Клокова Е.Е.

Ответ

• А или В или С или D – всегда будет истинно
• А и В и С и D – всегда будет ложно

Клокова Е.Е.

ПОДУМАЙ и ответь:

• Крыша одного дома несимметрична. Один скат её составляет с горизонталью угол 60 градусов, другой – угол 70 градусов. Предположим, что петух откладывает яйцо на гребень крыши. В какую сторону упаде яйцо – в сторону более пологого или более крутого ската?
• На границе США и Канады произошла авиационная катастрофа. В какой из двух стран, по вашему мнению, должны быть похоронены уцелевшие пассажиры?

Клокова Е.Е.

Логические функции

• Конъюнкция

• Дизъюнкция Инверсия Эквивалентность Импликация
• Дизъюнкция Инверсия Эквивалентность Импликация
• Дизъюнкция Инверсия Эквивалентность Импликация
• Дизъюнкция Инверсия Эквивалентность Импликация
• Дизъюнкция
• Инверсия
• Эквивалентность
• Импликация

Клокова Е.Е.

Конъюнкция

• Соответствует союзу И
• Обозначается знаком ^, *, &, and
• Иначе – логическое умножение

Конъюнкция двух переменных истинна тогда и только тогда, когда оба высказывания истинны

Клокова Е.Е.

Таблица истинности

Значения логической функции при разных сочетаниях значений входных переменных называют таблицей истинности.

Клокова Е.Е.

Алгоритм построения ТИ для простых высказываний

• Определить количество входных переменных (простых высказываний) n
• Определить количество комбинаций входных переменных по формуле: Q= 2 n
• Определить количество строк: К = Q + 1 ( строка для заголовка )
• Определить количество столбцов: K c = n + количество логических операций
• Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности.

Клокова Е.Е.

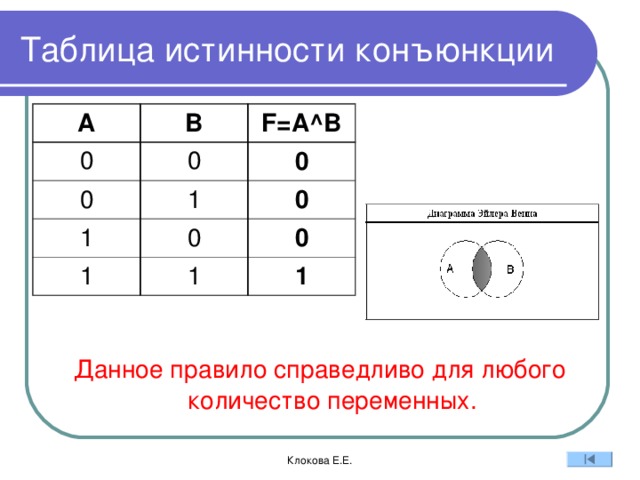
Таблица истинности конъюнкции

A

B

0

F=A^B

0

0

1

0

1

1

0

0

1

0

1

Данное правило справедливо для любого количество переменных.

Клокова Е.Е.

Дизъюнкция

• Соответствует союзу ИЛИ
• Обозначается знаком V, +, OR
• Иначе – логическое сложение

Дизъюнкция двух переменных ложна тогда и только тогда, когда оба высказывания ложны.

Клокова Е.Е.

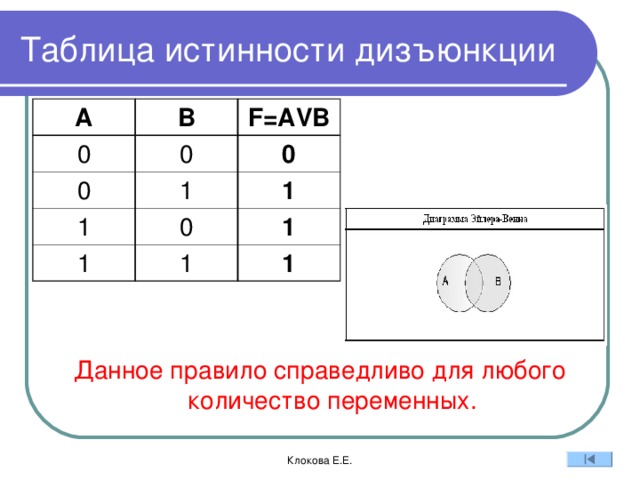
Таблица истинности дизъюнкции

A

B

0

0

F=AVB

0

1

1

0

1

0

1

1

1

1

Данное правило справедливо для любого количество переменных.

Клокова Е.Е.

Инверсия

• Соответствует частице НЕ
• Обозначается знаком подчеркивания над переменной – А, not, ¬
• Иначе – логическое отрицание

Инверсия истинна, если сама переменная ложна и наоборот, инверсия ложна, если сама переменная истина

Клокова Е.Е.

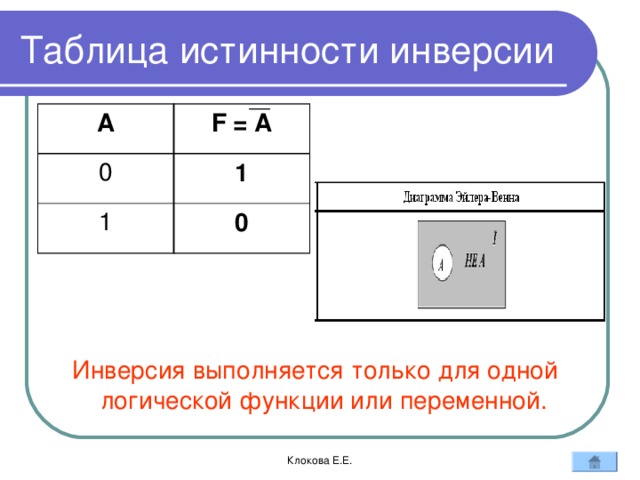
Таблица истинности инверсии

A

F = A

0

1

1

0

Инверсия выполняется только для одной логической функции или переменной.

Клокова Е.Е.

Эквивалентность

• Обозначается знаком или ~ ( тильда )
• Иначе – равносильность, равнозначность, логическое тождество, эквиваленция

Высказывание, составленное из двух высказываний при помощи связки  «тогда и только тогда, когда» , называется  эквивалентностью

Клокова Е.Е.

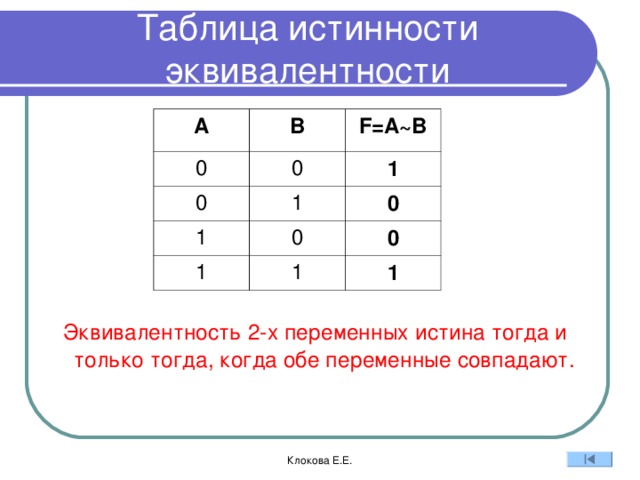
Таблица истинности эквивалентности

А

В

0

F=A~B

0

0

1

1

1

0

0

1

1

0

1

Эквивалентность 2-х переменных истина тогда и только тогда, когда обе переменные совпадают.

Клокова Е.Е.

, - Иначе – логическое следование, « если А, то В » Новое высказывание, полученное с помощью импликации, является ложным тогда и только тогда, когда условие А - истинно, а следствие В - ложно и истинно во всех остальных случаях.  Клокова Е.Е. " width="640"

Импликация

• Обозначается знаками =, -
• Иначе – логическое следование, « если А, то В »

Новое высказывание, полученное с помощью импликации, является ложным тогда и только тогда, когда условие А - истинно, а следствие В - ложно и истинно во всех остальных случаях. 

Клокова Е.Е.

B = A v B 0 0 1 1 1 1 0 1 0 1 1 Импликация 2-х переменных А и В ложно тогда, когда А – истинна, а В – ложна, в остальных случаях - истинна Клокова Е.Е. " width="640"

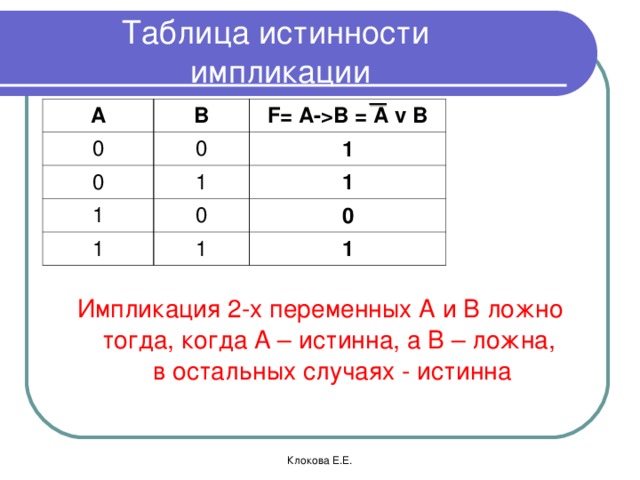
Таблица истинности импликации

А

B

0

F= A-B = A v B

0

0

1

1

1

1

0

1

0

1

1

Импликация 2-х переменных А и В ложно тогда, когда А – истинна, а В – ложна, в остальных случаях - истинна

Клокова Е.Е.

В Клокова Е.Е. " width="640"

Составьте логические выражения по сложным высказываниям

"Быть иль не быть - вот в чем вопрос." (В. Шекспир)

А V ¬ A В

"Если хочешь быть красивым, поступи в гусары." (К. Прутков)

А = В

Клокова Е.Е.

Приоритет логических операций:

• Инверсия
• Конъюнкция
• Дизъюнкция
• Импликация
• Эквивалентность

Клокова Е.Е.

Алгоритм построения ТИ для простых высказываний

• Определить количество входных переменных (простых высказываний) n
• Определить количество комбинаций входных переменных по формуле: Q = 2 n
• Определить количество строк: К = Q + 1 ( строка для заголовка )
• Расставить порядок выполнения логических операций с учетом их приоритета
• Определить количество столбцов: K c = n + количество логических операций
• Заполнить столбцы результатами выполнения логических операций в обозначенной последовательности.

Клокова Е.Е.