Презентация «Текстовые задачи: сложности и пути их решения»

Текстовые задачи: сложности и пути их решения

Подготовила

Пискарева Р.И.,

учитель математики

МОУ «Гимназия №1»

г.Железногорска Курской обл.

Научить решать текстовые задачи - значит, научить такому подходу к задаче, при котором она выступает как объект тщательного изучения, а её решение- как объект конструирования и изобретения.

Ученики должны знать : основные методы и приёмы решения текстовой задачи; классификацию текстовых задач и алгоритм их решения.

Уметь : определят тип текстовой задачи, знать особенности методики её решения, используя при этом разные способы; применять полученные математические знания в решении жизненных задач.

Для решения текстовых задач применяются три основных метода :

• Арифметический метод.
• Алгебраический метод.
• Комбинированный метод.

Арифметический метод.

• разбор условия задачи и составление плана её решения
• решение задачи по составленному плану
• проверка решения задачи.

Алгебраический метод.

• разборе условия задачи и составлении уравнения или неравенства по условию задачи.
• решение составленного уравнения или системы уравнений , неравенства или системы неравенств.
• проверка решения задачи

Решение задачи с помощью уравнения ( системы уравнений) обычно производится в такой последовательности:

• Вводятся переменные, т.е. обозначаются буквами величины. Которые требуется найти по условию задачи, либо те, которые необходимы для отыскания искомых величин.
• Составляют уравнение (систему уравнений). т. е. как бы «переводят» текст задачи на язык алгебры, формулируя равенство (систему равенств) алгебраических выражений.
• Решают составленное уравнение систему уравнений и из полученных решений отбирают те, которые подходят по смыслу задачи.

Комбинированный метод.

Этот метод получается в результате включения в алгебраический метод решения задач решения, в котором часть неизвестных величин определяется с помощью решения уравнений или системы уравнений, неравенств или системы неравенств, а другая часть - арифметическим методом.

Советы по решению текстовых задач

• Не просто прочитайте, а тщательно изучите условие задачи. Обращайте внимание на единицы измерения - они в течение всего решения должны быть одинаковы . Попытайтесь полученную информацию представить в другом виде- это может быт рисунок, таблица или просто краткая запись условия задачи.
• Выбор неизвестных.
• Составление и решение « математической модели »
• Обязательно проверить правильность записи числовых данных в условии задачи.
• Решение сложной текстовой задачи – процесс творческий. Иной раз требует вернуться к самому началу задачи, учитывая и анализируя уже полученные результаты.

Виды текстовых задач.

• Задачи на части, на нахождение дроби от числа и числа по его дроби и другого вида.
• Задачи на совместную работу.
• Задачи на движение.
• Задачи на проценты.
• Задачи на смеси и сплавы.
• Задачи на прогрессии.

Задачи на части, на нахождение дроби от числа и числа по его дроби и другого вида.

Задача 1 .( 5 класс)

Продолжительность жизни белого медведя 32 года, что составляет продолжительности жизни слона. Продолжительность жизни льва составляет жизни слона, что составляет жизни носорога. Какова продолжительность жизни каждого зверя ?

Решение

1) 32 : 4  25 = 200(лет) продолжительность жизни слона.

2) 200 : 5  1 =40(лет) живёт лев.

3) 40 : 5  6 = 48( лет) живёт носорог.

Ответ: 32 года - белый медведь;

40 лет - лев;

48 лет – носорог;

200 лет - слон.

Задача 2 ( из открытого банка заданий ОГЭ и ЕГЭ )

Среди 210000 жителей города не интересуется футболом и никогда не смотрят его по телевизору, а остальные являются футбольными болельщиками. Среди футбольных болельщиков смотрело по телевизору финальный матч Чемпионата Европы. Сколько жителей города не посмотрело этот матч.

Решение

1) 210000  =35000 (чел) не интересуются футболом.

2) 210000 - 35000 = 175000(чел) интересуются футболом (болельщики )

3)  175000 = 125000(чел) интересующихся футболом ( болельщики) смотрели по теле

175000 - 125 000 = 50 000 (чел) болельщиков не смотрели по телевизору матч.

Ответ: 50000 человек.

Задача 3 (открытый банк заданий на 1 бал)

В пакете 527 г. Смеси орехов, состоящие из миндаля, фундука и арахиса. Фундука в ней в 5 раз меньше чем арахиса и на 40г. больше , чем миндаля. Сколько фундука в пакете?

Решение

Так как масса всей смеси 527 грамм, то составим уравнение.

х+ ( х +40 ) +5( х + 40 )= 527

х + х +40 +5х +200 = 527

7х= 287

Х=41

41г - миндаля в пакете.

41 + 40 = 81(г) фундука в пакете.

Ответ : 81г.

Задачи на совместную работу.

Задача 1( 5 класс )

Отец с сыном могут покрасить забор за 4 часа. Отец справился бы с этой работой за 5 часов. Сколько часов потребуется сыну для выполнения той же работы?

Решение

1) 1 : 5 = (забора) покрасит отец за один час.

2) 1 : 4 = (забора) покрасят отец и сын за один час.

3) - = (забора) покрасит сын за один час.

4) 1 : = 20 (часов ) покрасит сын забор.

Ответ: 20 часов .

Задача 2 ( 2 часть на 2 балла )

Два строителя выложили стену из кирпичей за 14 дней, причём второй присоединился к первому через 3 дня после начала работы. Известно ,что второму строителю на выполнение всей работы потребовалось бы на 6 дней меньше ,чем первому . За сколько дней мог бы выложить эту стену каждый строитель, работая отдельно?

Решение

14  = часть работы, выполненная первым строителем.( х

11  часть работы, выполненная вторым строителем.

Так как объём всей выполненной работы равен 1, то составим уравнение.

+ = 1 (  х(х-6)) ≠0

14х -84 + 11х = -6х

- 31х + 84 =0

не удовлетворяет условию

х = 28

за 28 дней первый строитель может выложит стену.

28-6= 22(дня) может выложить второй строитель стену.

Ответ: 28 дней, 22 дня.

Задача 3.

Четыре бригады должны разгрузит вагон с продуктами .Вторая. третья и четвёртая могут выполнит эту работу за 4 часа, первая, третья и четвёртая - 3часа. Если будут работать только первая и вторая, то вагон будет разгружен за 6 часов. За какое время могут разгрузить вагон все четыре бригады?

Решение

у + а + в =(вагона) разгрузят вторая, третья и четвёртая за 1 час.

х + а + в =(вагона) разгрузят первая, третья и четвёртая за 1 час.

х + у = ( вагона) ) разгрузят первая, и вторая за 1 час.

Сложим уравнения получим:

2х + 2у + 2а +2в = ( :2 )

Х + у + а + в = (вагона) разгрузят четыре бригады за 1 час.

1: = (часа) разгрузят вагон четыре бригады вместе.

Ответ: часа.

Задачи на движение ( задачи на движение по реке )

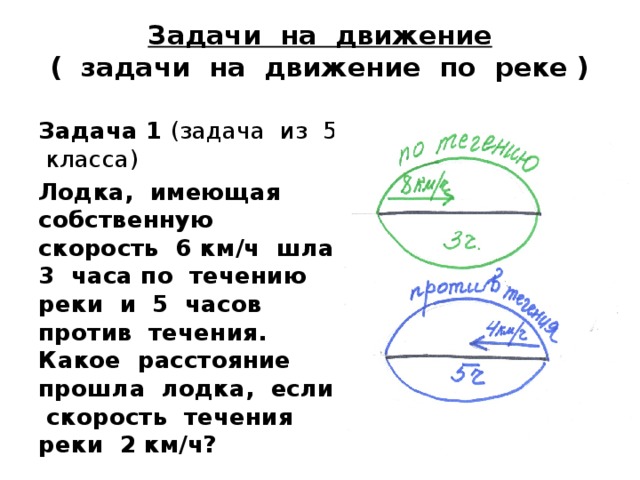
Задача 1 (задача из 5 класса)

Лодка, имеющая собственную скорость 6 км/ч шла 3 часа по течению реки и 5 часов против течения. Какое расстояние прошла лодка, если скорость течения реки 2 км/ч?

Собственная скорость лодки - 6 км/ч

(скорость в стоячей или неподвижной воде)

Скорость течения реки (скорость плота) - 2 км/ч

Скорость по течению - 1) 6 + 2 = 8(км/ч)

Скорость против течения - 2) 6 - 2 = 4(км/ч)

3) 8  3 = 24( км) расстояние по течению реки.

4) 5  4 = 20 ( км) расстояние против течения реки.

5) 24 +20 = 44 (км) прошла лодка.

Ответ: 44 км.

Задачи на движение

Задача 2 (из открытого банка заданий, 2часть)

Расстояние между пристанями А и В равно 48 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В тот час повернула обратно и возвратилась в А . К этому времени плот проплыл 25 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки 5 км/ч.

Собственная скорость лодки - х км/ч, х 5

(скорость в стоячей или неподвижной воде)

Скорость течения реки (скорость плота) - 5км/ч

Скорость по течению - (х +5)км/ч

Скорость против течения - (х - 50) (км/ч)

  25 : 5 = 5 (ч) время движения плота.

Так как лодка отправилась вслед за ним через час, значит 5 - 1 = 4 (ч)- время движения лодки.

Так как время движения лодки 4 часа, то составим уравнение:

+ = 4 ( (х - 5 ) (х +5 ))0

− 60 +12х + 60 = - 25

- 24х - 25 = 0

− 1 не удовлетворяет условию х

25км/ч собственная скорость лодки.

Ответ : 25км/ч.

Задачи на проценты

Задача 1.

Свежие фрукты содержат 80% воды, а высушенные - 28% . Сколько потребуется свежих фруктов для приготовления 80 кг высушенных фруктов.

Решение.

100% - 80% = 20% - процентное содержание сухой массы в свежих фруктах.

100% - 72% =28% -процентное содержание сухой массы в сухих фруктах.

 х –кг масса сухой массы в свежих фруктах

 80 - кг масса сухой массы в сушеных фруктах .

Так как масса сухой массы одинакова, то составим уравнение.

 х =  80

20  х = 72  80

Х = х =284

284 кг необходимо свежих фруктов.

Ответ: 284кг.

Задачи на смеси и сплавы

Имеются два сплава. Первый содержит 5% никеля, второй- 25 % никеля. Из этих двух сплавов получили третий сплав массой 250 кг, содержащий 20 % никеля. На сколько килограммов масса первого сплава меньше массы второго сплава ?

  х + у = 250

 х +  у =  250

Х +у = 250

5 х + 25у = 20  250

Х + у =250

Х +5у = 1000

4у = 750

у = 187,5

187,5 кг - масса второго сплава.

250 - 187,5 =62,5 кг - масса первого сплава.

187,5 - 62,5 =125 кг- масса первого сплава меньше второго.

Ответ : 125 кг.

Задачи на прогрессии

Задача 1

Рабочие прокладывают тоннель длиной 112 метров, ежедневно увеличивая норму прокладки на одно и то же число метров. Известно, что за первый день рабочие проложил 7м туннеля. Определите, сколько метров туннеля проложили рабочие в последний день, если вся работа была выполнена за 7 дней.

Решение.

112 м. – сумма 7 членов арифметической прогрессии.

7- первый член.

Х м - количество метров, которые надо проложить в последний день.

=  7

 7

224 =( 7 + х )  7

224 = 49 +7х

7х =175

Х = 25

25 метров туннеля проложили рабочие в последний день

Ответ : 25м.