Применение производной при решении задач ЕГЭ
Определение производной
Производной функции f(x) (f'(x0)) в точке x0 называется число, к которому стремится разностное отношение  , стремящемся к нулю.
, стремящемся к нулю.
 =
= 
1. На рисунке изображены график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции  в точке
в точке 

2. 
На рисунке изображён график функции  и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой  . Найдите значение производной функции
. Найдите значение производной функции  в точке
в точке  .
.
Геометрический смысл производной:
Производная в точке x0 равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке
f/ (x0) = k = tq α.


4.
На рисунке изображен график функции y=f(x), определенной на интервале (−3; 9). Найдите количество точек, в которых производная функции f(x) равна 0.
5. На рисунке изображен график функции y=f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 8. Найдите f'(8).
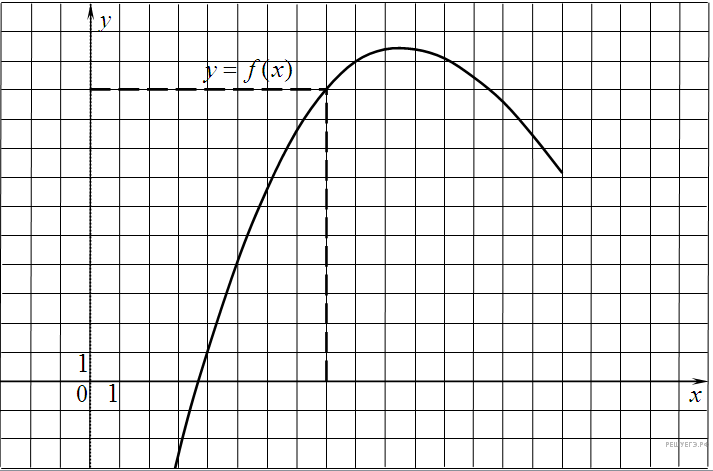
6. На рисунке изображен график функции y = f(x), определенной на интервале (−6; 5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = −6.

7.
На рисунке изображен график производной функции f(x), определенной на интервале (−9; 3). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = 2x − 19 или совпадает с ней.
8. Прямая  является касательной к графику функции
является касательной к графику функции  . Найдите c.
. Найдите c.
9. Прямая  является касательной к графику функции
является касательной к графику функции  . Найдите абсциссу точки касания.
. Найдите абсциссу точки касания.
Физический смысл производной:
S/(t) = v(t).
Материальная точка движется прямолинейно по закону 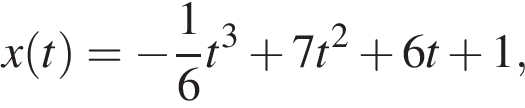 где х — расстояние от точки отсчёта (в метрах), t — время движения (в секундах). Найдите её скорость (в метрах в секунду) в момент времени t = 6 с.
где х — расстояние от точки отсчёта (в метрах), t — время движения (в секундах). Найдите её скорость (в метрах в секунду) в момент времени t = 6 с.
Материальная точка движется прямолинейно по закону  (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 5 м/с?
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). В какой момент времени (в секундах) ее скорость была равна 5 м/с?
Материальная точка движется от начального до конечного положения. На рисунке изображён график её движения. На оси абсцисс откладывается время в секундах, на оси ординат — расстояние от начального положения точки (в метрах). Найдите среднюю скорость движения точки. Ответ дайте в метрах в секунду.
Исследование функции на монотонность и экстремумы
Если производная в точке х0 меняет свой знак с «+» на «-», то х0 – точка максимума.
Если производная в точке х0 меняет свой знак с «-» на «+», то х0 – точка минимума.
Если на промежутке I f/(x) 0, то f(x) на I возрастает, f/(x) f(x) на I убывает.
1. На рисунке изображен график производной функции  , определенной на интервале . Найдите количество точек максимума функции
, определенной на интервале . Найдите количество точек максимума функции  на отрезке
на отрезке  .
.
2. На рисунке изображён график y = f'(x) — производной функции f(x), определённой на интервале (−3; 11). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
3. На рисунке изображен график функции  , определенной на интервале . Определите количество целых точек, в которых производная функции отрицательна.
, определенной на интервале . Определите количество целых точек, в которых производная функции отрицательна.
4. На рисунке изображён график функции y = f(x) и шесть точек на оси абсцисс: x1, x2, x3, …, x6. В скольких из этих точек производная функции f(x) положительна?
5. На рисунке изображён график функции  , определенной на интервале . Сколько из отмеченных точек принадлежат промежуткам убывания функции?
, определенной на интервале . Сколько из отмеченных точек принадлежат промежуткам убывания функции?
6. На рисунке изображен график производной функции f(x), определенной на интервале (−8; 4). В какой точке отрезка [−7; −3] f(x) принимает наименьшее значение?
7.
На рисунке изображен график производной функции f(x), определенной на интервале (−16; 4). Найдите количество точек экстремума функции f(x) на отрезке [−14; 2].
8. На рисунке изображен график производной функции  , определенной на интервале . В какой точке отрезка
, определенной на интервале . В какой точке отрезка 
 принимает наименьшее значение?
принимает наименьшее значение?
9.
На рисунке изображен график производной функции f(x), определенной на интервале (−8; 6). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
1 0. На рисунке изображен график функции y = f(x), определенной на интервале (−2; 12). Найдите сумму точек экстремума функции f(x).
Задачи с прикладным содержанием
1. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием см. Расстояние  от линзы до лампочки может изменяться в пределах от 55 до 70 см, а расстояние
от линзы до лампочки может изменяться в пределах от 55 до 70 см, а расстояние  от линзы до экрана — в пределах от 260 до 300 см. Изображение на экране будет четким, если выполнено соотношение . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.
от линзы до экрана — в пределах от 260 до 300 см. Изображение на экране будет четким, если выполнено соотношение . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.
2.Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием см. Расстояние  от линзы до лампочки может изменяться в пределах от 330 до 350 см, а расстояние
от линзы до лампочки может изменяться в пределах от 330 до 350 см, а расстояние  от линзы до экрана — в пределах от 80 до 105 см. Изображение на экране будет четким, если выполнено соотношение . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.
от линзы до экрана — в пределах от 80 до 105 см. Изображение на экране будет четким, если выполнено соотношение . Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы еe изображение на экране было чeтким. Ответ выразите в сантиметрах.
6. Задачи на оптимизацию
1. Первичная информация разделяется по серверам №1 и №2 и обрабатывается на них. С сервера №1 при объёме t2 Гбайт входящей в него информации выходит 20t Гбайт, а с сервера №2 при объёме t2 Гбайт входящей в него информации выходит  Гбайт обработанной информации; 25 t
Гбайт обработанной информации; 25 t
2. Алексей вышел из дома на прогулку со скоростью v км/ч. После того, как он прошел 6 км, из дома следом за ним выбежала собака Жучка, скорость которой была на 9 км/ч больше скорости Алексея. Когда Жучка догнала хозяина, они повернули назад и вместе возвратились домой со скоростью 4 км/ч. Найдите значение v, при котором время прогулки Алексея окажется наименьшим. Сколько при этом составит время его прогулки?
3. В 1-е классы поступает 43 человека: 23 мальчика и 20 девочек. Их распределили по двум классам: в одном должно получиться 22 человека, а в другом ― 21. После распределения посчитали процент мальчиков в каждом классе и полученные числа сложили. Каким должно быть распределение по классам, чтобы полученная сумма была наибольшей?
4. У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 500 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а на втором – 500 ц/га.
Фермер может продать картофель по цене 5000 руб. за центнер, а свёклу — по цене 8000 руб. за центнер. Какой наибольший доход может получить фермер?
5. Два велосипедиста равномерно движутся по взаимно перпендикулярным дорогам по направлению к перекрестку этих дорог. Один из них движется со скоростью 40 км/ч и находится на расстоянии 5 км от перекрестка, второй движется со скоростью 30 км/ч и находится на расстоянии 3 км от перекрестка. через сколько минут расстояние между велосипедистами станет наименьшим? Каково будет это наименьшее расстояние.

























