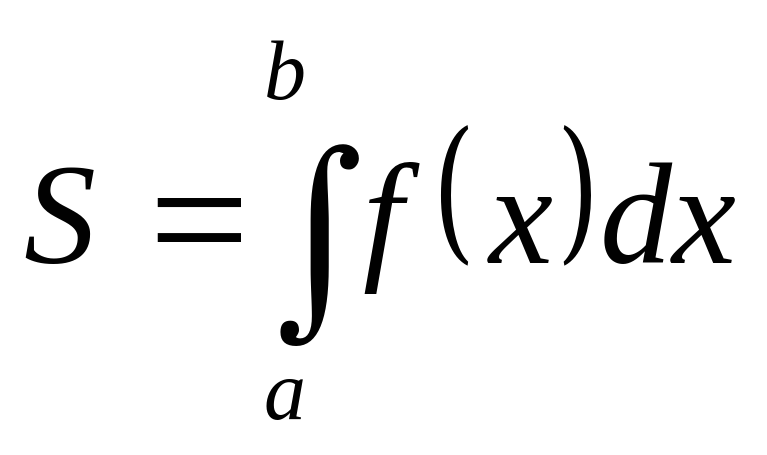ПЛАН-КОНСПЕКТ УЧЕБНОГО ЗАНЯТИЯ
Применение интеграла к вычислению площадей плоских фигур.
-
| ФИО | Волобуева Светлана Яковлевна |
-
| Место работы | ГБПОУ «Агротехнический техникум» с.Дивное |
-
| Должность | Преподаватель математики |
-
| Предмет | Математика |
-
| Курс | 1 |
-
| Тема и номер урока в теме | Применение интеграла к вычислению площадей плоских фигур. |
-
| Базовый учебник | электронный Учебник А.Н.Колмогорова Алгебра и начала анализа 10-11 класс http://catalog.prosv.ru/item/4828
|
Цель и задачи занятия
Цель:
- формирование умения вычислять площади плоских фигур с помощью интегралов.
Задачи:
- проверить усвоение понятия «криволинейная трапеция», формулы Ньютона – Лейбница; подвести обучающихся к выводу формул для нахождения площадей фигур
- научить вычислять площади фигур с помощью интегралов, отработать алгоритм нахождения площадей фигур с помощью интегралов.
- воспитание познавательной активности, уверенности в себе.
Тип занятия: сообщение новых знаний (тема рассчитана на 45 мин)
Формы работы обучающихся: фронтальная работа, самостоятельная работа
Необходимое техническое оборудование: компьютер, мультимедийный проектор
Используется проблемный метод, дифференцированный подход
Структура и ход занятия
СОДЕРЖАНИЕ УРОКА
I Организационный момент( приветствие, проверка наличия обучающихся, инструктаж по т/б, п/б сообщение темы и цели урока)- 3 мин
II Актуализация опорных знаний
На этом этапе актуализируются опорные знания, необходимые обучающимся для восприятия новой темы.
Актуализация проводится с помощью фронтальной работы.
С каким важным понятием мы работали на предыдущих уроках? (интеграл) ЦОР 14 http://school-collection.edu.ru/catalog/rubr/a87d6303-ae07-46dd-a18a-855c725fb448/?interface=catalog&class[]=54&subject[]=17
Что вам известно об этом понятии?
Сформулируйте правила нахождения интеграла
индивидуальная работа 5 обучающихся проходят тест на компьютере. Работа продолжается 10 минут Результат выдается по окончанию тестирования.
Цор 20 http://school-collection.edu.ru/catalog/rubr/a87d6303-ae07-46dd-a18a-855c725fb448/?interface=catalog&class[]=54&subject[]=17
Содержание теста
1 найти первообразную функции
2 выберите графики(нарисованы красным цветом), тех функций которые являются первообразными для данных прямых(нарисованы синим цветом), изображенных на рисунке
3 на рисунке изображен график функции y=ax2+bx+c и четыре прямые, укажите номер той прямой, для которой квадратичная функция является первообразной.
4 найдите общий вид первообразных для функции
5 дана функция f(x)=3x2, постройте график первообразной, проходящий через точку
А(2;6)
6 укажите первообразную первообразную F(x) функции f(x)=2/x^2, на промежутке (0;∞),что F(x)=10
7 для функции постройте график первообразной, принимающей заданное значение в данной точке f(x)=3 F(-1)=5
III изучение нового материала:
устно сформулируйте С помощью формулы Ньютона-Лейбница вычисляют
А)первообразную Б) площадь криволинейной трапеции в) интеграл г) производную
А если фигура не является криволинейной трапецией, как найти ее площадь? Я думаю, что вы поняли, чему будет посвящен сегодняшний урок. Запишите тему урока: «Вычисление площадей плоских фигур с помощью определенного интеграла».
На предыдущих занятиях мы вычисляли площади криволинейных трапеций.
Какая фигура называется криволинейной трапецией?
Сегодня мы продолжим решать задачи на нахождение площадей различных фигур с помощью интегралов.
ЦОР15 http://school-collection.edu.ru/catalog/rubr/a87d6303-ae07-46dd-a18a-855c725fb448/?interface=catalog&class[]=54&subject[]=17
Содержание :
Вычисление площади фигуры с помощью интеграла. Пример.
Как вычислить площадь фигуры, ограниченной линиями: y = f (x); y = 0; x = a; x = b.(криволинейная трапеция)
Выполнить записи в тетрадях.
Как вычислить площадь фигуры, ограниченной линиями: y = f (x); y = 0; x = a; x = b
На экран выводится ЦОР 15
теория 1. Применение интеграла к вычислению площади фигуры.
ВОПРОС Можем ли мы найти площадь данной фигуры, используя формулы 1 или 2? ( Нет).Обучающиеся делают вывод о том, что данная фигура не является криволинейной трапецией, а следовательно формулы 1 или 2 использовать нельзя.
Возникает проблема: Как можно найти площадь данной фигуры?
Обучающиеся пробуют найти ответ и убеждаются, что с помощью известных формул площадь данной фигуры найти нельзя.
Ставится учебная цель – вывести формулу для нахождения площади данной фигуры.
Вернемся к формулам 1 и 2. Данные формулы справедливы для нахождения площади криволинейных трапеций.
Выход из затруднения: Обучающиеся выдвигают предположение: попытаться из представленной фигуры выделить криволинейные трапеции, площади которых мы находить умеем.
Из рисунка видно, что данная фигура состоит из криволинейных трапеций, следовательно, искомая площадь равна разности площадей этих трапеций.

Рассматривается пример, когда площадь фигуры состоит из суммы двух площадей
ЦОР 15 теория 2 Вычисление площади фигуры с помощью интеграла.
IV закрепление нового материала
Перед выполнением работы, преподаватель вместе с обучающимися составляет алгоритм нахождения площади фигур.
Алгоритм выполнения задания.
1.В прямоугольной системе координат изобразите графики соответствующих функций.
2.Заштрихуйте фигуру, площадь которой нужно найти.
3.Запишите формулу для вычисления площади данной фигуры в общем виде.
4.Запишите данную формулу с использованием данных функций.
5.Определите пределы интегрирования
6.Вычислите площадь.
Коллективное выполнение упражнений №360 (б,г) электронный Учебник А.Н.Колмогорова Алгебра и начала анализа 10-11 класс http://catalog.prosv.ru/item/4828
V Самостоятельная работа.
Используется дифференцированный подход.
Задание для обучающихся занимающихся на «4»и «5»: №360 (б,г) электронный Учебник А.Н.Колмогорова Алгебра и начала анализа 10-11 класс
Задание для обучающихся уровня «3»:
карточка-инструкция
Вычислите площадь фигуры, ограниченной линиями у = 2- х2, у = х2
Алгоритм выполнения задания.
1.В прямоугольной системе координат изобразите графики функций у = 2- х2
и у = х2.
2.Заштрихуйте фигуру, площадь которой нужно найти.
3.Запишите формулу для вычисления площади данной фигуры в общем виде.
4.Запишите данную формулу с использованием данных функций.
5.Определите пределы интегрирования
6.Вычислите площадь.
VI Итог урока
Сегодня на уроке мы рассмотрели два варианта нахождения площадей фигур с помощью интегралов, формулы для их нахождения вы вывели сами. Составили алгоритм нахождения этих площадей. Применили данный алгоритм к решению задач.
VII. Домашнее задание.
электронный учебник А.Н.Колмогорова Алгебра и начала анализа 10-11 класс
№ 364(а,б) 365 (а,б)