Применение производной к исследованию функций и построению графиков.

МБОУ

«Кольская СОШ № 2»

КОНСПЕКТ

УРОКА ПО МАТЕМАТИКЕ

В 10 КЛАССЕ

Занятие по теме:

«Применение производной к исследованию функций и построению графиков.»

Учитель математики

Антипин Александр Александрович

Дисциплина: Математика

Преподаватель: Антипин А.А.

Дата проведения:

Класс: 10

Тема урока: Применение производной к исследованию функций и построению графиков.

Тип урока: лекция-практикум

Вид урока: комбинированный

Цели урока:

1. Обучающие:

   • обеспечить усвоение студентами основных понятий ранее изученных тем;

   • научить применять таблицу производных при исследовании функций и построении графиков;

   • организовать деятельность учащихся по самостоятельному применению знаний в разнообразных ситуациях.

2. Развивающие:

   • развитие познавательного интереса к дисциплине;

   • развитие внимания, логического мышления.

3. Воспитывающие:

   • формирование навыков по применению знаний, полученных на уроке в жизни;

   • воспитание мотивов учения, положительного отношения к знаниям.

Оснащение урока: интерактивная доска, программа для просмотра презентаций Power Point.

Макроструктура урока:

1. Организационный момент (2-3 мин)

2. Мотивация (1-2 мин)

3. Актуализация опорных знаний и умений (10 мин)

4. Изучение нового материала (45-50 мин)

5. Восприятие и осмысление нового материала (5-8 мин)

6. Первичное закрепление (7-10 мин)

7. Домашнее задание (1-2 мин)

8. Подведение итогов. Выставление и комментирование оценок (2-3 мин)

9. Рефлексия (1-2 мин)

Ход урока:

1. Организационный момент

   • приветствие;

   • проверка отсутствующих.

2. Мотивация

• сообщение цели и темы урока;

• представление плана урока.

1. Актуализация опорных знаний и умений

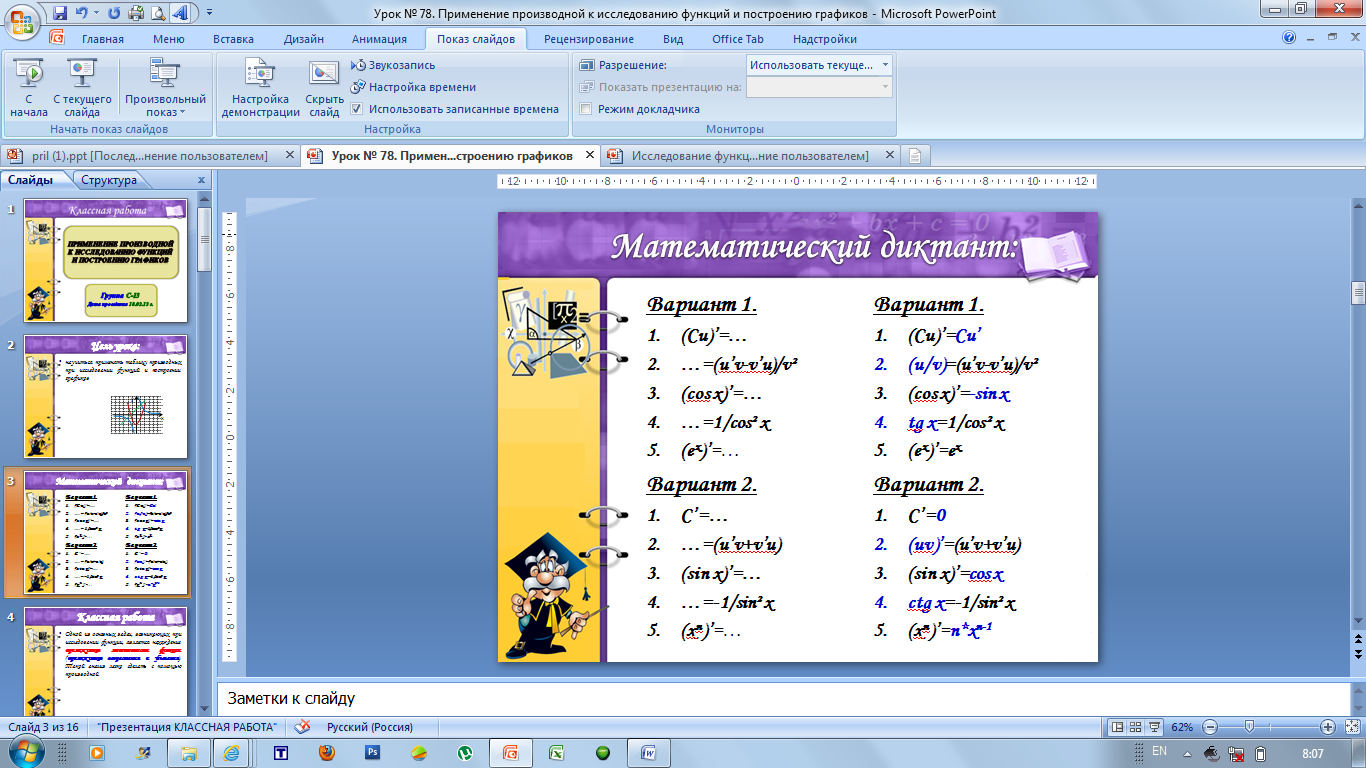
Проводится математический диктант на знание таблицы производных:

1. Изучение нового материала

Понятие производной – одно из важнейших в математике. С помощью производной учитывая её механический смысл и геометрический смысл, можно решать самые разнообразные задачи, относящиеся к любой области человеческой деятельности. В частности, с помощью производных стало возможным подробное исследование функций, что позволило очень точно строить их графики, находить их наибольшие и наименьшие значения и т. д.

Одной из основных задач, возникающих при исследовании функции, является нахождение промежутков монотонности функции (промежутков возрастания и убывания). Такой анализ легко сделать с помощью производной.

Но прежде чем приступить к исследованию функций на монотонность вспомним, какие функции называются возрастающими (убывающими).

Функция y=f(x) называется возрастающей в некотором интервале, если в точках этого интервала большему значению аргумента соответствует большее значение функции, и убывающей, если большему значению аргумента соответствует меньшее значение функции.

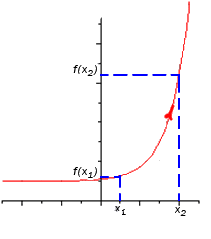
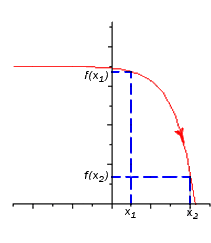
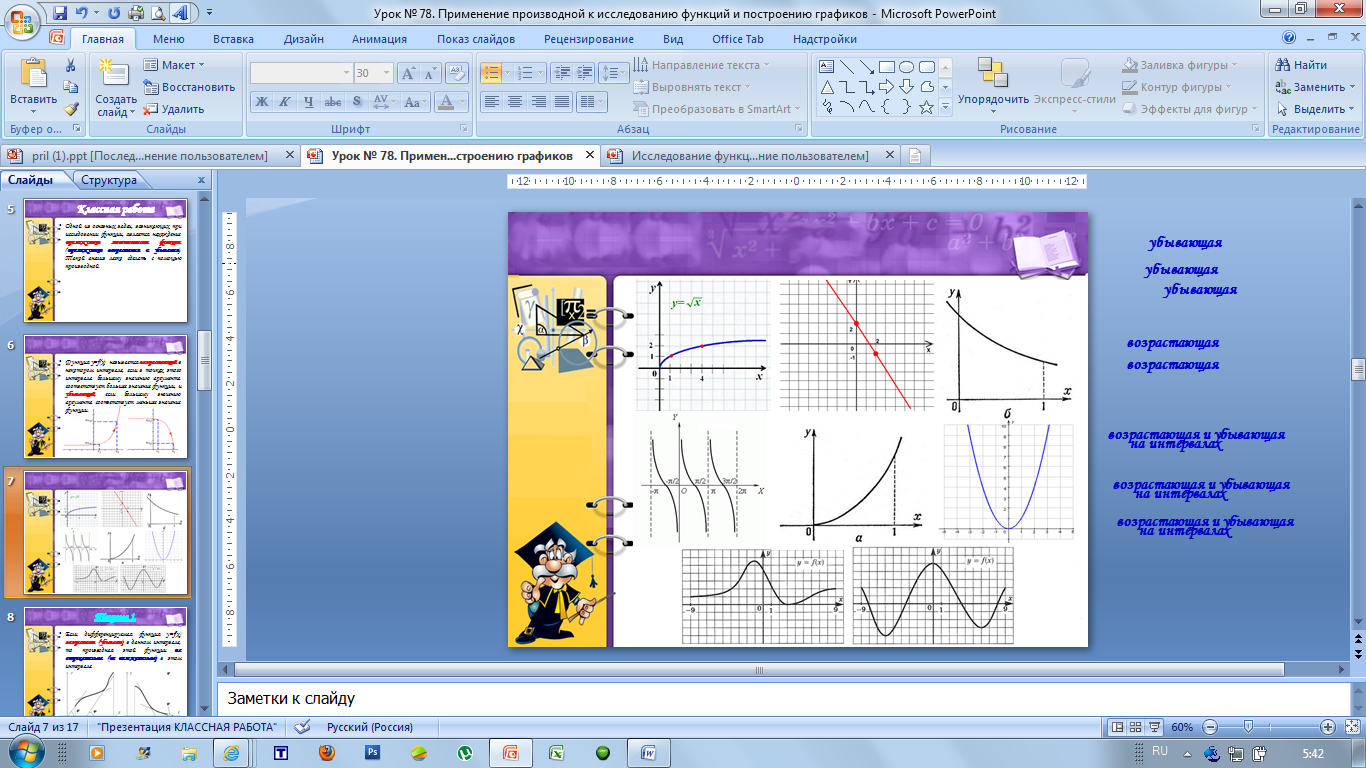
На слайде 8 графиков функций. Определите, какие из них являются возрастающими, какие убывающими, или не являются ни теми, ни другими.

Необходимый признак возрастания (убывания) функции.

Теорема 1. Если дифференцируемая функция y=f(x) возрастает (убывает) в данном интервале, то производная этой функции не отрицательна (не положительна) в этом интервале.

Обратное заключение также справедливо, оно выражается следующей теоремой.

Теорема 2. Если производная функции y=f(x) отрицательна (положительна) на некотором интервале, то функция в этом интервале монотонно возрастает (монотонно убывает).

Сформулируем теперь правило нахождения интервалов монотонности функции f(x).

1. Находим область определения функции f(x).

2. Вычисляем производную f’(x) данной функции.

3. Находим точки, в которых f’(x)=0 или не существует. Эти точки называются критическими для функции f(x).

4. Делим область определения функции этими точками на интервалы. Они являются интервалами монотонности.

5. Исследуем знак f’(x) на каждом интервале. Если f’(x)›0, то на этом интервале f(x) возрастает; если f’(x)‹0, то на таком интервале функция f(x) убывает.

Рассмотрим теперь нахождение промежутков возрастания/убывания на конкретном примере функции.

Пример №1. Найти промежутки монотонности функции y=2x³-3x²-36x+5.

1. Область определения: R. Функция непрерывна.

2. Вычисляем производную : y’=6x²-6x-36.

3. Находим критические точки: y’=0.

x²-x-6=0

Д=1-4*(-6)*1=1+24=25

x₁=-2, x₂=3

1. Делим область определения на интервалы:

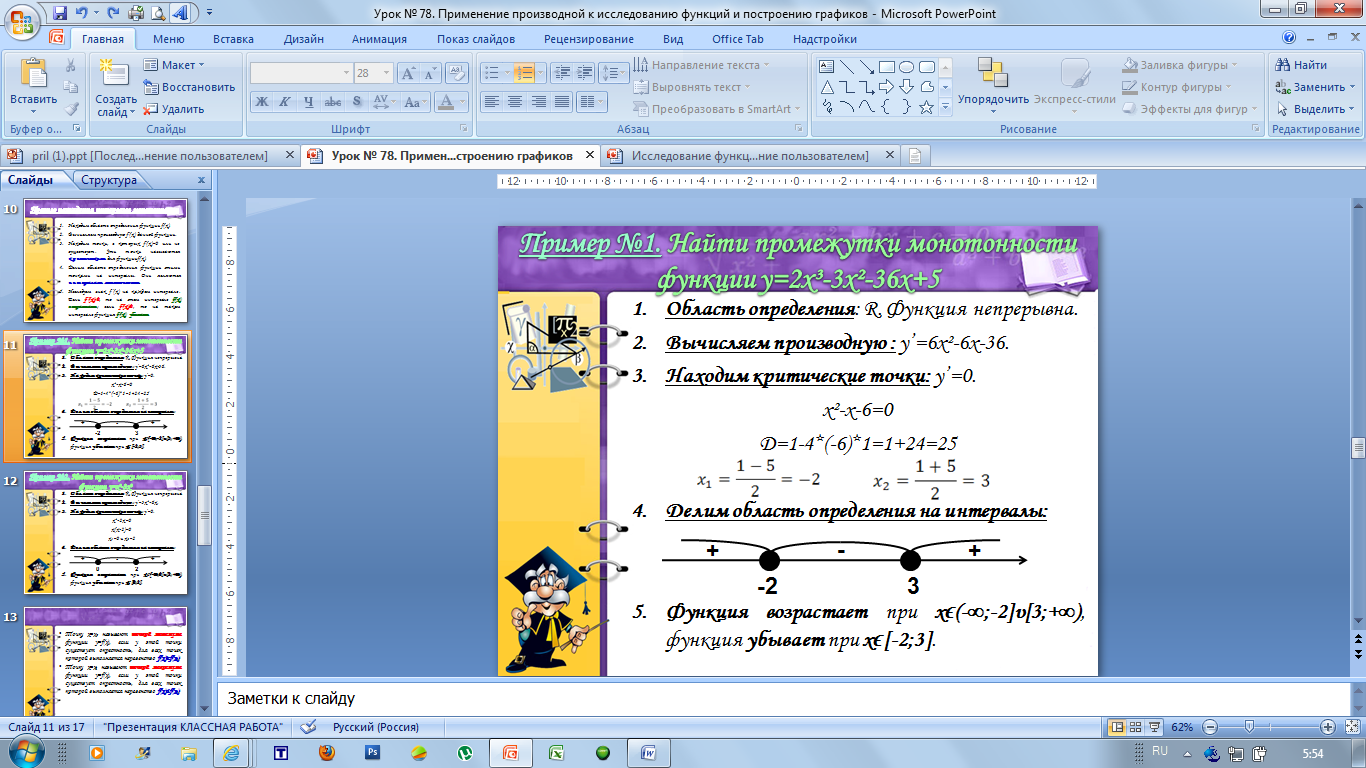
1. Функция возрастает при xϵ(-∞;-2]υ[3;+∞), функция убывает при xϵ[-2;3].

Пример №2. Найти промежутки монотонности функции y=x³-3x².

1. Область определения: R. Функция непрерывна.

2. Вычисляем производную : y’=3x²-6x.

3. Находим критические точки: y’=0.

x²-2x=0

x(x-2)=0

x1=0 и x2=2

1. Делим область определения на интервалы:

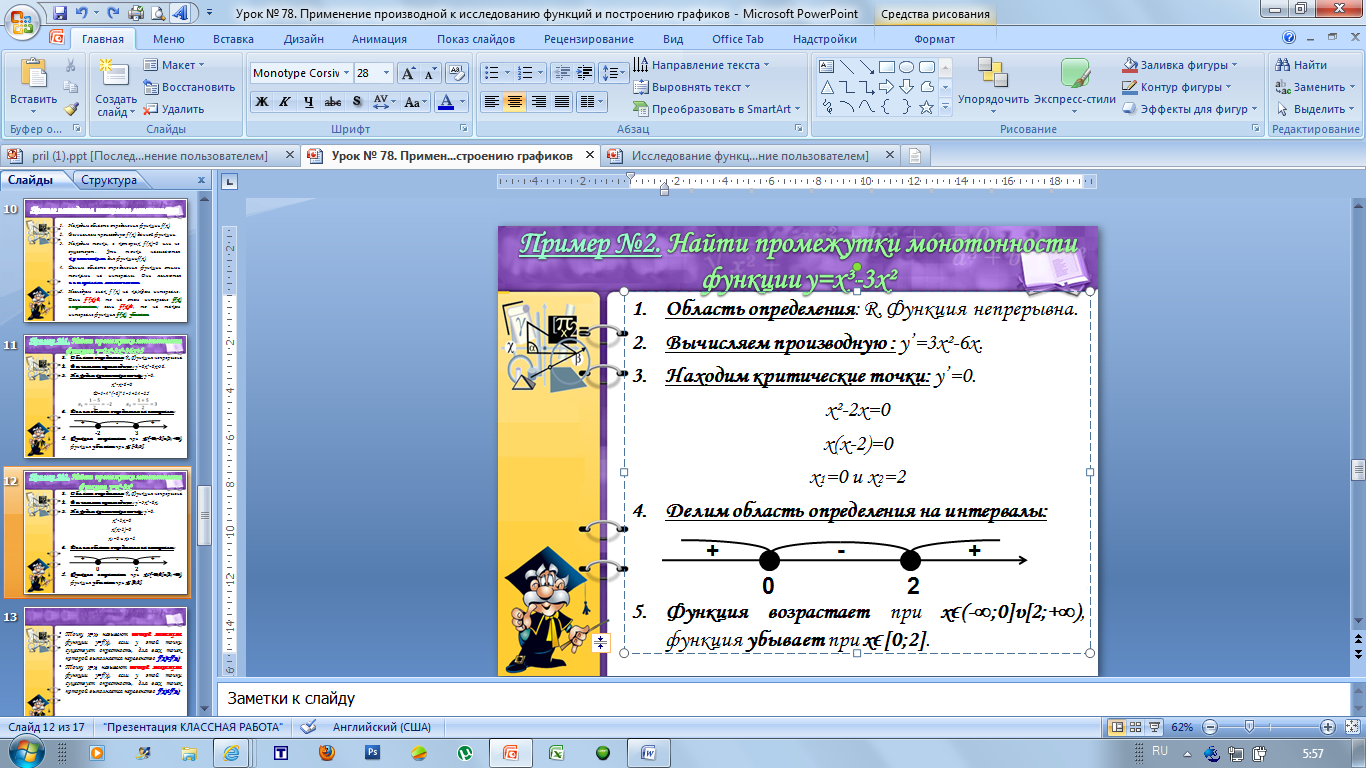
1. Функция возрастает при xϵ(-∞;0]υ[2;+∞), функция убывает при xϵ[0;2].

Но помимо монотонности функций с помощью первой производной можно ещё определить экстремумы функций (точки максимума/минимума).

Сначала введём необходимые определения и понятия.

Опр. 1. Точку x=x₀ называют точкой минимума функции y=f(x), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x)≥f(x₀).

Опр. 2. Точку x=x₀ называют точкой максимума функции y=f(x), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x)≤f(x₀).

Теорема 3. Если функция y=f(x) имеет экстремум в точке x=x₀, то в этой точке производная функции или равна нулю, или не существует.

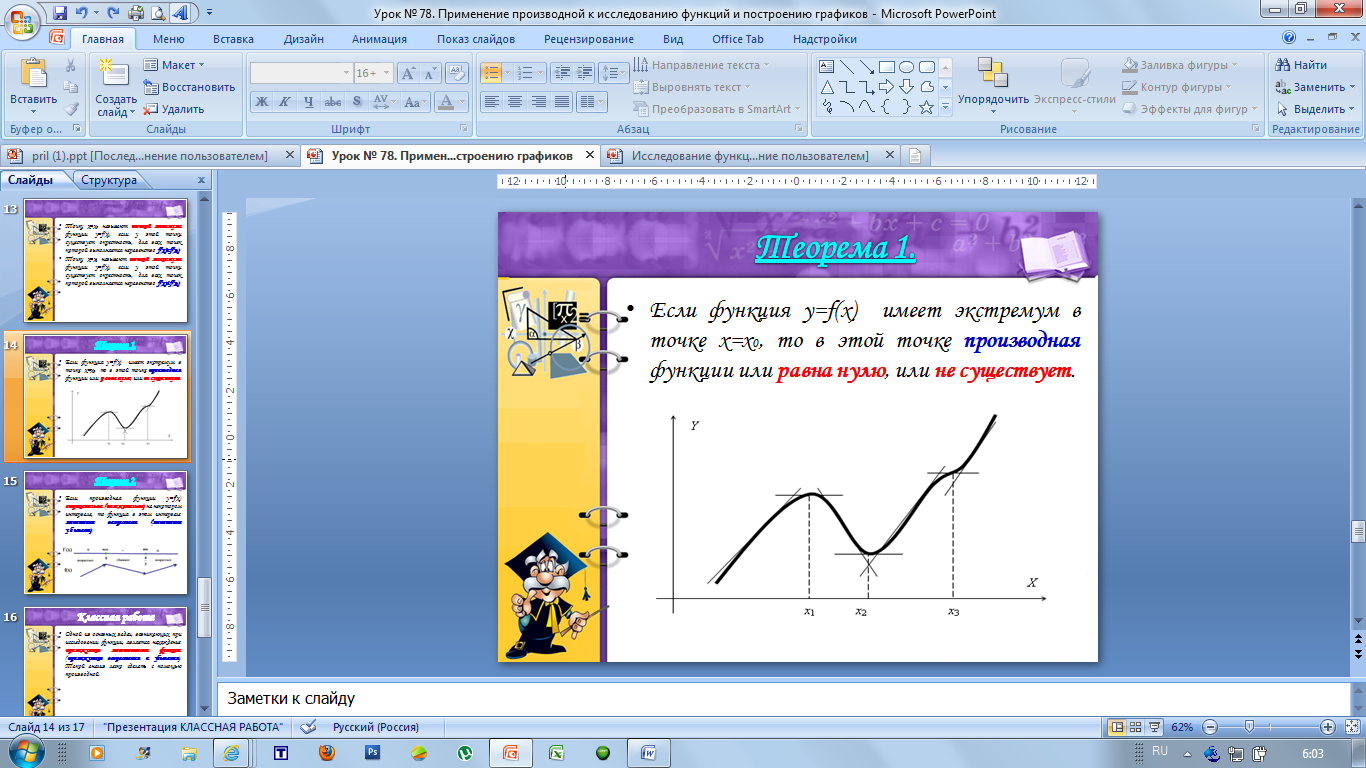
Заметим, что теорема 3 является только необходимым (но не достаточным) условием существования экстремума: из того, что производная f’(x) в точке x0 обращается в нуль, не обязательно следует, что в этой точке функция имеет экстремум.

Например, функция f(x)=x⁵ имеет производную f’(x)=5x⁴, которая обращается в нуль в точке x₀=0. Однако экстремума в этой точке функция не имеет (происходит изменение кривизны).

Поэтому вводят ещё достаточный признак существования экстремумов функции.

Теорема 4. Если производная f’(x) при переходе через точку x₀ меняет знак, то точка x₀ является точкой экстремума функции f(x).

Если производная меняет знак с + на –, то точка будет являться точкой максимума, если с – на +, то точка будет точкой минимума.

Рассмотрим теперь на примерах исследование функции на монотонность и экстремумы.

Пример №3. Найти экстремумы функции y=-2x³-3x²+12x-4.

1. Область определения: R. Функция непрерывна.

2. Вычисляем производную : y’=-6x²-6x+12.

3. Находим критические точки: y’=0.

x²+x-2=0

D=1-4*1*(-2)=1+8=9

x₁=-2 и x₂=1

1. Делим область определения на интервалы:

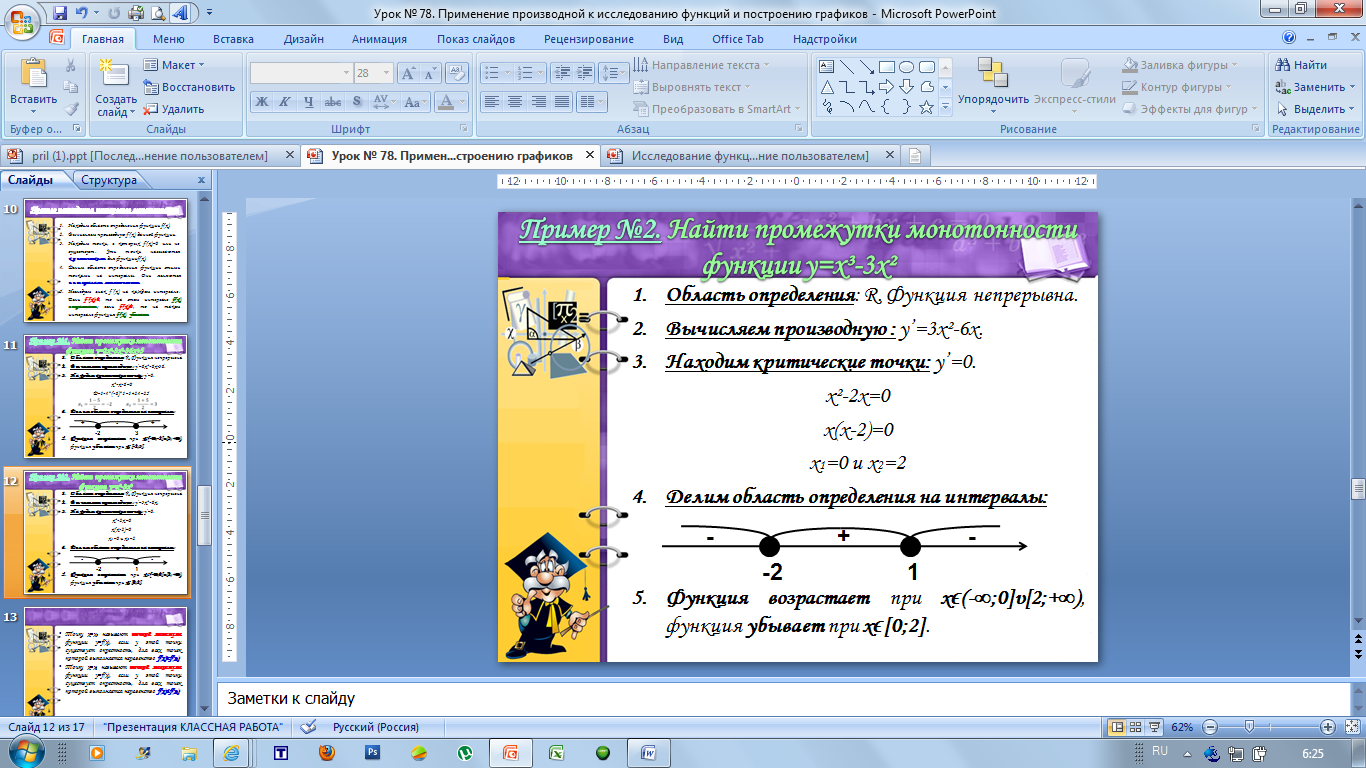
1. Функция возрастает при xϵ(-∞;0]υ[2;+∞), функция убывает при xϵ[0;2].

2. Видно, что в точке x=-2 знак производной меняется с минуса на плюс. Поэтому критическая точка x=-2 – точка минимума. Найдём минимум функции y_min=-24. В точке x=1 знак меняется с плюса на минус. Поэтому критическая точка x=1 – точка максимума. Найдём максимум функции: y_max=3.

1. Восприятие и осмысление нового материала

   1. Определение возрастающей (убывающей) функции.

   2. Теорема о возрастании (убывании) функции.

   3. Точка минимума (максимума) функции.

   4. Стационарные и критические точки производной.

   5. Достаточные условия экстремума функции.

   6. Алгоритм исследования функции на монотонность и экстремумы.

2. Первичное закрепление.

3. Задание на дом: выучить достаточные и необходимые условия монотонности и существования экстремумов функции.

4. Подведение итогов. Выставление и комментарий оценок.

5. Рефлексия