Признаки параллельности прямых.

Тема: Признаки параллельности

двух прямых.

Цель:

дать определение

параллельных прямых ,

доказать первый признак

параллельности двух прямых.

Новый материал.

1.Как на плоскости могут располагаться две прямые?

а)могут иметь общую

точку

а ∩ в

пересекаются

б) могут не иметь

общих точек

параллельные

а | | в

Дайте определение параллельных прямых.

Определение: Две прямые на плоскости называются

параллельными, если они не пересекаются.

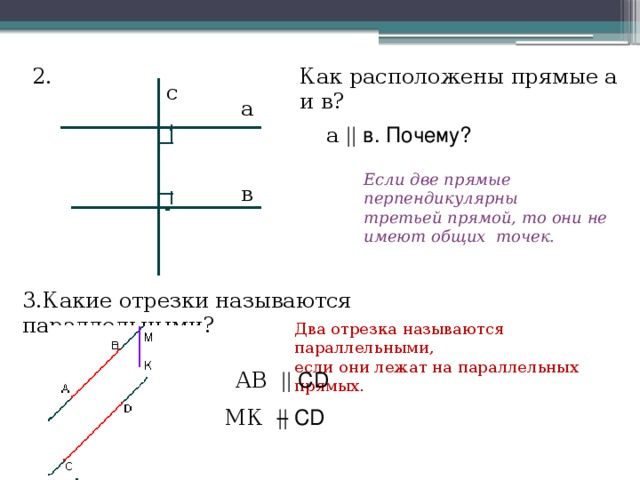
Как расположены прямые а и в?

2.

с

а

а || в. Почему?

Если две прямые перпендикулярны

третьей прямой, то они не имеют общих точек.

в

3.Какие отрезки называются параллельными?

Два отрезка называются параллельными,

если они лежат на параллельных прямых.

АВ || СD

МК || СD

3.Определение секущей.

Прямая с называется секущей

относительно прямых а и в , если

она пересекает их в двух точках .

Углы:3 и 5, 4 и 6- накрест лежащие

углы;

Углы: 4 и 5, 3 и 6- односторонние углы;

Углы: 1 и 5,4 и 8, 2 и 6, 3 и 7 –

соответственные углы.

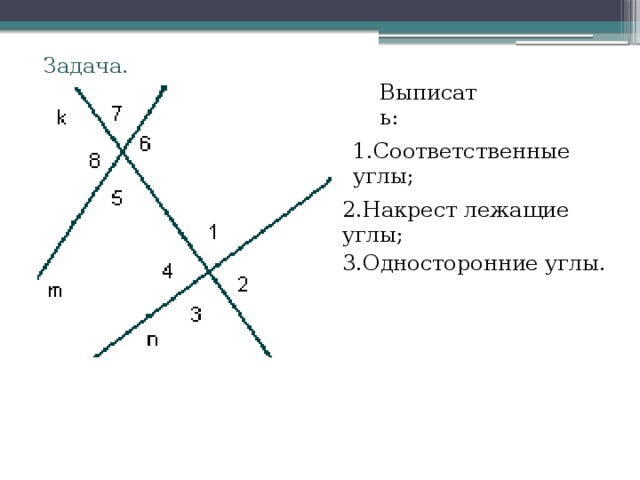
Задача.

Выписать:

1.Соответственные углы;

2.Накрест лежащие углы;

3.Односторонние углы.

4.Первый признак параллельности двух прямых.

Теорема:

Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Дано: а, в, с- секущая,

∟ 1= ∟ 2.

Доказать: а || в.

Доказательство:

∟ 1= ∟ 2=90 ○

Случай 1.

а ┴ АВ, в ┴ АВ, такие прямые не

пересекаются, значит (по определению)

а || в.

∟ 1 и ∟ 2- не прямые.

Случай 2.

Для доказательства

1.Разделим отрезок АВ на равные отрезки, т.е. АО=ОВ.

2.Проведем ОН ┴ а.

3.Отложим отрезок ВН1 на прямой в

такой, что ВН1=АН.

4.Рассмотрим ∆ ОНА и ∆ ВОН1.

1).ОА=ОВ – по построению;

2). ∟ 1= ∟ 2-по условию;

3) АН=ВН1- по построению.

Значит ∆ АОН=∆ ВОН1по двум сторонам и углу между ними.

Следовательно а || в.

В равных треугольниках соответственные элементы равны.

∟ 3= ∟ 4, значит точка Н1 лежит на продолжении луча НО,т.е.

точки Н,О,Н1- лежат на одной прямой.

∟ 5= ∟ 6= 90 ○ , в ┴ НН1.

Значит а ┴ НН1, в ┴ НН1,т.е. прямые а и в не имеют общих точек.

Задача 1.

Параллельны прямые а и в, если

1) ∟ 1= ∟ 3;

2) ∟ 1= ∟ 4;

3) ∟ 5= ∟ 6= 90 ○ .

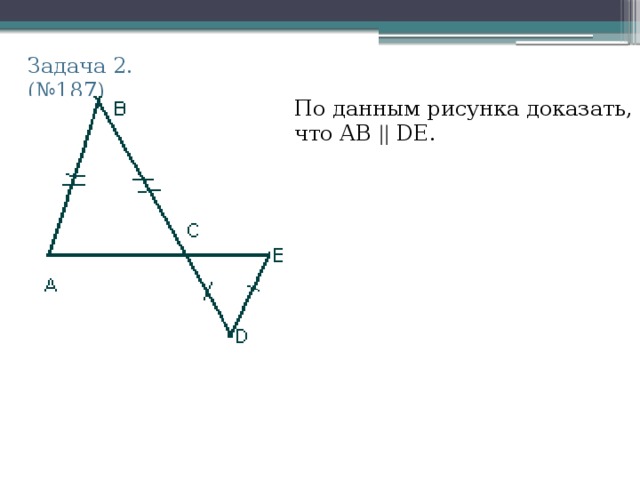
Задача 2. (№187)

По данным рисунка доказать,

что АВ || DE.

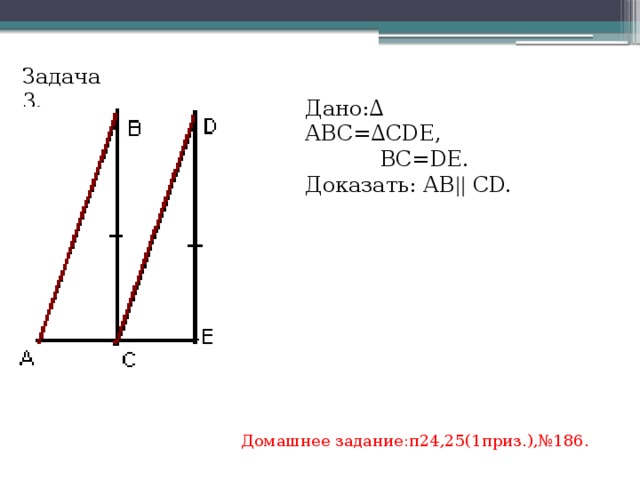
Задача 3.

Дано:∆ АВС=∆СDE,

ВС=DE.

Доказать: АВ || СD.

Домашнее задание:п24,25(1приз.),№186.