Пробный вариант 3 математика 2016.
1. Задание 1 № 341323. Найдите значение выражения 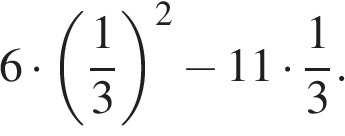
Решение.
Вынесем общий множитель за скобки:
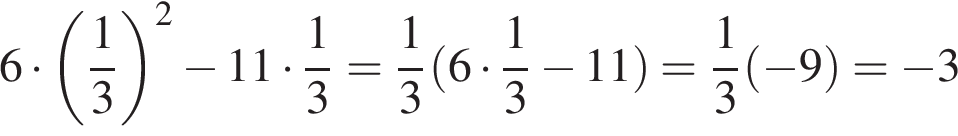
Ответ: -3.
Ответ: -3
341323
-3
Источник: СтатГрад: Тренировочная работа по математике 07.04.2015 вариант МА90701.
2. Задание 2 № 337358. На координатной прямой отмечено число a.

Найдите наименьшее из чисел a2, a3, a4.
В ответе укажите номер правильного варианта.
1) a2
2) a3
3) a4
4) не хватает данных для ответа
Решение.
Заметим, что 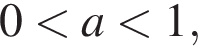 откуда следует, что
откуда следует, что 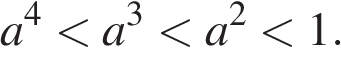 Таким образом, наименьшее из представленных в ответе чисел — число
Таким образом, наименьшее из представленных в ответе чисел — число 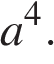
Правильный ответ указан под номером: 3.
Ответ: 3
337358
3
3. Задание 3 № 317389. Найдите значение выражения 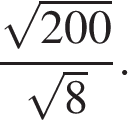
В ответе укажите номер правильного варианта.
1) 5
2) 
3) 
4) 40
Решение.
Найдём значение выражения:
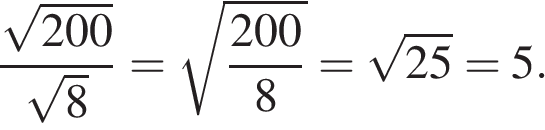
Правильный ответ указан под номером: 1.
Ответ: 1
317389
1
4. Задание 4 № 314572. Найдите корни уравнения 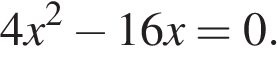
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
Решение.
Вынесем общий множитель за скобки:
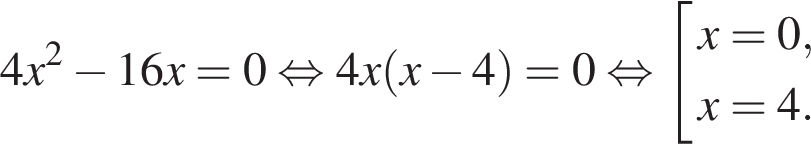
Ответ: 0; 4.
Ответ: 0;4
314572
0;4
Источник: Банк заданий ФИПИ
5. Задание 5 № 138. Установите соответствие между графиками функций и формулами, которые их задают.
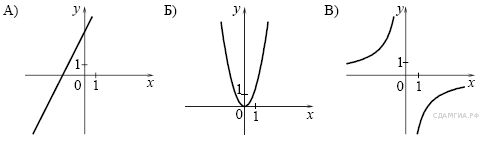
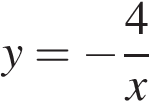
1) 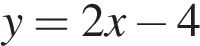
2) 
3) 
4) 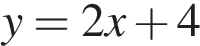
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке.
Решение.
Определим вид графика каждой из функций:
1) 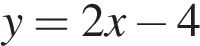
 уравнение прямой c точкой пересечения
уравнение прямой c точкой пересечения 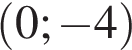 с осью ординат
с осью ординат 
2) 
 уравнение гиперболы.
уравнение гиперболы.
3) 
 уравнение параболы, ветви которой направленны вверх.
уравнение параболы, ветви которой направленны вверх.
4) 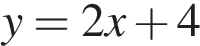
 уравнение прямой c точкой пересечения
уравнение прямой c точкой пересечения 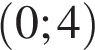 с осью ординат
с осью ординат 
Тем самым найдено соответствие: A — 4, Б — 3, В — 2.
Ответ: 432.
Ответ: 432
138
432
Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1313.
6. Задание 6 № 341225. Последовательность задана условиями 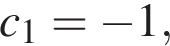
 Найдите
Найдите 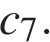
Решение.
Последовательно вычислим: c2 = −2, c3 = −3, c4 = −4, c5 = −5, c6 = −6, c7 = −7.
Примечание.
Данная последовательность образует арифметическую прогрессию. Найдем разность арифметической прогрессии:
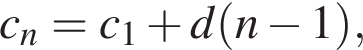
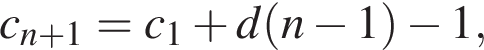 тогда
тогда 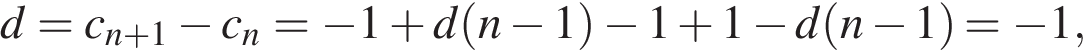
Зная разность и первый член арифметической прогрессии, можно найти  посредственно:
посредственно:
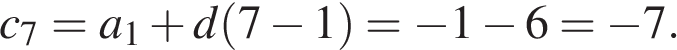
Ответ: −7.
Ответ: -7
341225
-7
Источник: Банк заданий ФИПИ
7. Задание 7 № 338131. Найдите значение выражения 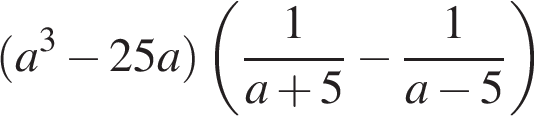 при
при 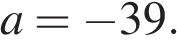
Решение.
Приведём в скобках к общему знаменателю:
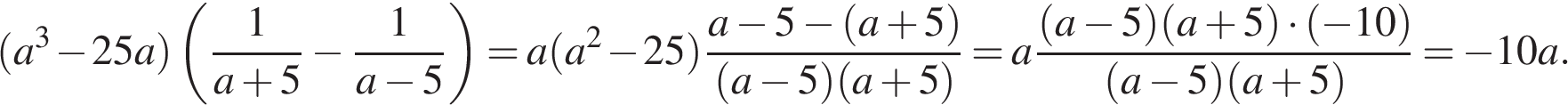
Подставим значение 

Ответ: 390.
Ответ: 390
338131
390
8. Задание 8 № 314604. 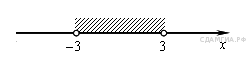 Решение какого из данных неравенств изображено на рисунке?
Решение какого из данных неравенств изображено на рисунке?
В ответе укажите номер правильного варианта.
1) 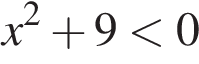
2) 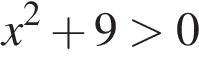
3) 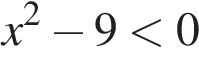
4) 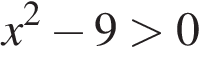
Решение.
Решим каждое из неравенств:
1) 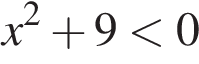 — решений нет.
— решений нет.
2) 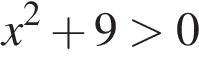 — верно для всех
— верно для всех 
3) 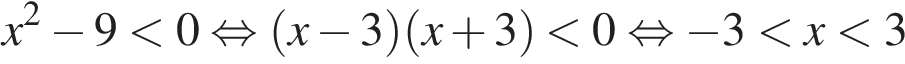
4) 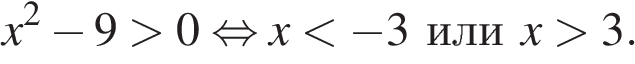
Правильный ответ указан под номером 3.
Ответ: 3
314604
3
Источник: Банк заданий ФИПИ
9. Задание 9 № 311458. 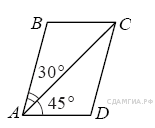 Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.
Решение.
Так как угол А равен 75°, а сумма односторонних углов параллелограмма равна 180°, больший угол параллелограмма равен 105°.
Ответ: 105.
Ответ: 105
311458
105
Источник: ГИА-2013. Математика. Экзамен. Вариант 9
10. Задание 10 № 311494. 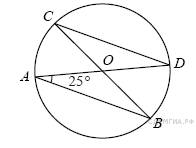 В окружности с центром в точке O проведены диаметры AD и BC, угол OAB равен 25°. Найдите величину угла OCD.
В окружности с центром в точке O проведены диаметры AD и BC, угол OAB равен 25°. Найдите величину угла OCD.
Решение.
Углы BCD и OAB являются вписанными и опираются на одну дугу BD. Поэтому ∠OAB = ∠BCD = ∠OCD = 25°.
Ответ: 25.
Ответ: 25
311494
25
Источник: ГИА-2013. Математика. Экзамен. Вариант 10
11. Задание 11 № 169880. Одна из сторон параллелограмма равна 12, другая равна 5, а тангенс одного из углов равен 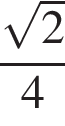 . Найдите площадь параллелограмма.
. Найдите площадь параллелограмма.
Решение.
Площадь параллелограмма равна произведению сторон на синус угла между ними. Найдем синус угла. В прямоугольном треугольнике тангенс определяется как отношение противолежащего катета к прилежащему. Имеем:
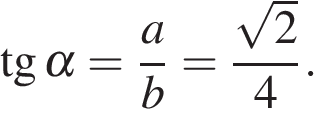
Таким образом, 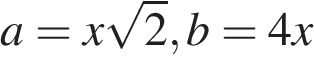 , где x — число.
, где x — число.
По теореме Пифагора гипотенуза этого прямоугольного треугольника равна:
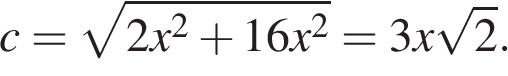
.
В прямоугольном треугольнике синус определяется как отношение противолежащего катета к гипотенузе. Имеем:
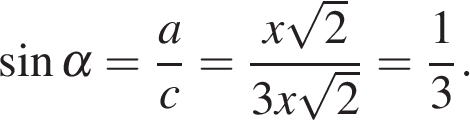
Таким образом,
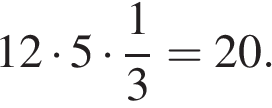
Ответ: 20.
Ответ: 20
169880
20
12. Задание 12 № 316285. 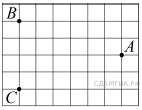 На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах.
На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах.
Решение.
Расстояние от точки А до середины отрезка ВС равно шести сторонам клетки, или 6 см.
Ответ: 6.
Ответ: 6
316285
6
Источник: МИОО: Диагностическая работа по математике 01.10.2013 вариант МА90107.
13. Задание 13 № 145. Укажите номера верных утверждений.
1) Центры вписанной и описанной окружностей равностороннего треугольника совпадают.
2) Существует квадрат, который не является ромбом.
3) Сумма углов любого треугольника равна 180° .
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
Решение.
-------------------
Дублирует 315121
Проверим каждое из утверждений.
1) «Центры вписанной и описанной окружностей равностороннего треугольника совпадают» — верно, т.к. совпадают точки пересечения биссектрис и серединных перпендикуляров этого треугольника.
2) «Существует квадрат, который не является ромбом» — неверно; верным будет утверждение: «Существует ромб, который не является квадратом».
3) «Сумма углов любого треугольника равна 180°» — верно по свойству треугольника.
Ответ: 1; 3.
Ответ: 1; 3
145
1; 3
Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1313.
14. Задание 14 № 30. В таблице приведены нормативы по бегу на 30 метров для учащихся 9-х классов.
|
| Мальчики | Девочки |
| Отметка | «5» | «4» | «3» | «5» | «4» | «3» |
| Время, секунды | 4,6 | 4,9 | 5,3 | 5,0 | 5,5 | 5,9 |
Какую отметку получит девочка, пробежавшая эту дистанцию за 5,36 секунды?
В ответе укажите номер правильного варианта.
1) Отметка «5».
2) Отметка «4».
3) Отметка «3».
4) Норматив не выполнен.
Решение.
Девочка пробежала дистанцию не так быстро, чтобы получить «5», но достаточно быстро, чтобы получить «4».
Правильный ответ указан под номером 2.
Ответ: 2
30
2
Источник: Демонстрационная версия ГИА—2013 по математике.
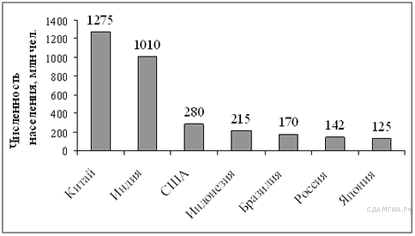
15. Задание 15 № 315200. На диаграмме представлены некоторые из крупнейших по численности населения стран мира.
Численность населения какого государства примерно в 6 раз меньше численности населения Китая? В ответе напишите численность населения этого государства в млн чел.
Решение.
Из диаграммы видно, что численность населения Китая 1275 млн чел., следовательно, государство с численностью населения примерно в 6 раз меньше должно иметь численность населения около 1275 : 6 = 212,5 млн чел. Из диаграммы видно, что такое государство — Индонезия.
Ответ: 215.
Ответ: 215
315200
215
Источник: Банк заданий ФИПИ
16. Задание 16 № 318186. Клубника стоит 180 рублей за килограмм, а виноград – 160 рублей за килограмм. На сколько процентов клубника дороже винограда?
Решение.
Клубника дороже винограда на 180 − 160 = 20 рублей. Разделим 20 на 160:
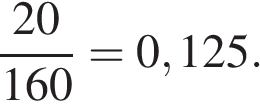
Значит, клубника дороже винограда на 12,5%.
Ответ: 12,5.
Ответ: 12,5
318186
12,5
17. Задание 17 № 311358. 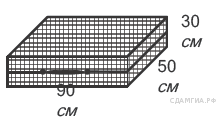 Дизайнер Павел получил заказ на декорирование чемодана цветной бумагой. По рисунку определите, сколько бумаги (в см2) необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность чемодана, если каждую грань он будет обклеивать отдельно (без загибов).
Дизайнер Павел получил заказ на декорирование чемодана цветной бумагой. По рисунку определите, сколько бумаги (в см2) необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность чемодана, если каждую грань он будет обклеивать отдельно (без загибов).
Решение.
Найдем площади всех деталей, которые необходимо обклеить:
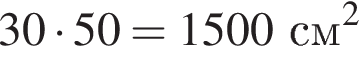
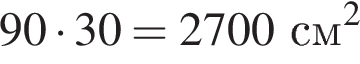
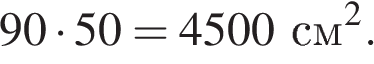
Так как чемодан имеет по две одинаковых детали, вся площадь, которую необходимо обклеить равна

Ответ: 17400.
Ответ: 17400
311358
17400
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар. 4)
18. Задание 18 № 341530. Средний рост игроков в баскетбол в школьной мужской сборной составляет 175 см. Рост Кирилла из этой сборной составляет 175 см. Какое из следующих утверждений верно?
1) Обязательно найдётся игрок, помимо Кирилла, ростом 175 см.
2) Кирилл — самый низкий в сборной команде по баскетболу.
3) Обязательно найдётся игрок ростом менее 175 см.
4) Обязательно найдётся игрок, помимо Кирилла, ростом не менее 175 см.
В ответе запишите номер выбранного утверждения.
Решение.
Первое утверждение неверно: например, в команде могут быть три игрока ростом 175 см, 176 см и и 174 см.
Второе утверждение неверно: пример из п. 1.
Третье утверждение неверно: все игроки могут быть ростом 175 см.
Четвёртое утверждение верно: так как если будет игрок ниже 175 см., то для того, чтобы средний рост был 175 см. нужен игрок выше 175 см.
Ответ: 4.
Ответ: 4
341530
4
Источник: СтатГрад: Тренировочная работа по математике 07.05.2015 вариант МА90902.
19. Задание 19 № 341390. На экзамене 60 билетов, Стас не выучил 6 из них. Найдите вероятность того, что ему попадется выученный билет.
Решение.
Стас выучил 60 − 6 = 54 билета, значит вероятность того, что ему попадется один из них равна 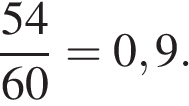
Ответ: 0,9.
Ответ: 0,9
341390
0,9
Источник: СтатГрад: Тренировочная работа по математике 07.04.2015 вариант МА90703.
20. Задание 20 № 311530. Площадь трапеции 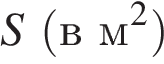 можно вычислить по формуле
можно вычислить по формуле 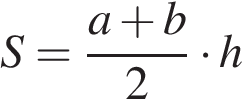 , где
, где 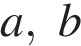 — основания трапеции,
— основания трапеции, 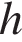 — высота (в метрах). Пользуясь этой формулой, найдите высоту
— высота (в метрах). Пользуясь этой формулой, найдите высоту 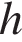 , если основания трапеции равны
, если основания трапеции равны 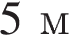 и
и 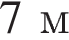 , а её площадь
, а её площадь 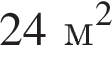 .
.
Решение.
Выразим высоту трапеции из формулы площади:
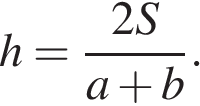
Подставляя, получаем:
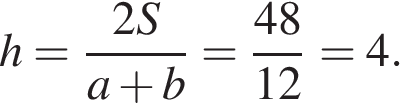
Ответ: 4.
Приведём другое решение.
Подставим в формулу известные значения величин:
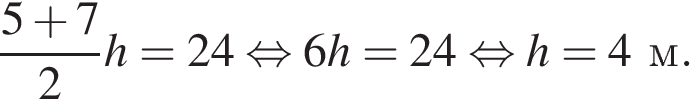
Ответ: 4
311530
4
Источник: 9 класс. Математика. Краевая диагностическая работа. Краснодар (вар.6)
21. Задание 21 № 338522. Решите систему неравенств 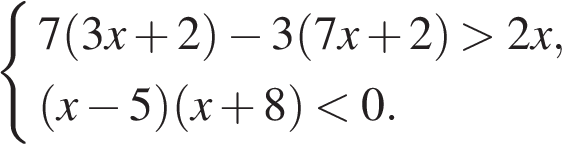
Решение.
Последовательно получаем:
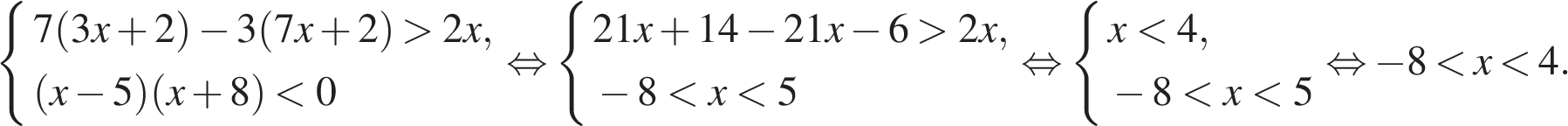
Ответ: 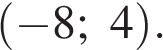
22. Задание 22 № 333319. Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 30 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 144 км, скорость первого велосипедиста равна 24 км/ч, скорость второго — 28 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
Решение.
За то время, пока первый велосипедист делал остановку, второй велосипедист проехал 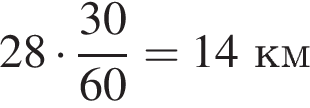 . Всё остальное время они одновременно находились в пути, значит, второй велосипедист за это время проехал
. Всё остальное время они одновременно находились в пути, значит, второй велосипедист за это время проехал 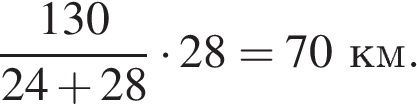 Таким образом, суммарно он проехал 84 км.
Таким образом, суммарно он проехал 84 км.
Ответ: 84 км.
Источник: МИОО: Тренировочная работа по математике 06.05.2014 вариант МА90701.
23. Задание 23 № 341129. Постройте график функции 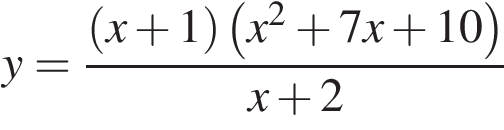 и определите, при каких значениях
и определите, при каких значениях  прямая
прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
Решение.
Преобразуем выражение:
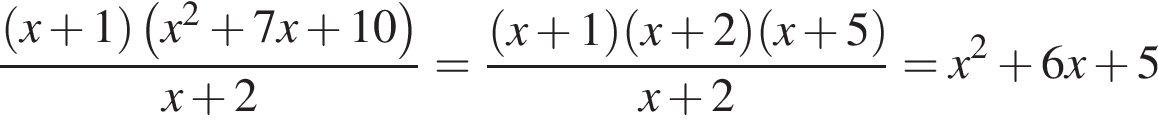 при условии, что
при условии, что 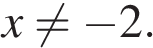
Построим график:
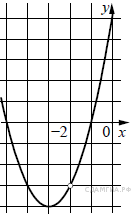
Прямая  имеет с графиком ровно одну общую точку при
имеет с графиком ровно одну общую точку при 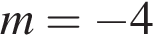 и при
и при 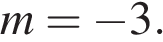
Ответ: −4; −3.
Источник: СтатГрад: Диагностическая работа по математике 10.02.2015 вариант МА90501.
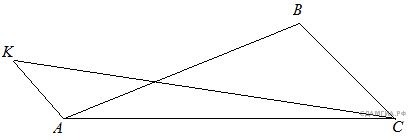
24. Задание 24 № 314897. Стороны AC, AB, BC треугольника ABC равны 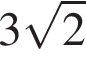 ,
, 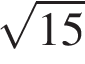 и 1 соответственно. Точка K расположена вне треугольника ABC, причём отрезок KC пересекает сторону AB в точке, отличной от B. Известно, что треугольник с вершинами K, A и C подобен исходному. Найдите косинус угла AKC, если ∠KAC90°.
и 1 соответственно. Точка K расположена вне треугольника ABC, причём отрезок KC пересекает сторону AB в точке, отличной от B. Известно, что треугольник с вершинами K, A и C подобен исходному. Найдите косинус угла AKC, если ∠KAC90°.
Решение.
Рассмотрим подобные треугольники 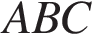 и
и 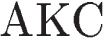 и установим соответствие между их углами. Против большей стороны всегда лежит больший угол, в треугольнике
и установим соответствие между их углами. Против большей стороны всегда лежит больший угол, в треугольнике 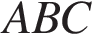 это угол
это угол 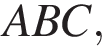 в треугольнике
в треугольнике  , в свою очередь, есть тупой угол
, в свою очередь, есть тупой угол  и он является наибольшим, значит
и он является наибольшим, значит  Угол
Угол 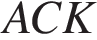 заведомо не может быть равен углу
заведомо не может быть равен углу  так как он составляет только его часть. Следовательно угол
так как он составляет только его часть. Следовательно угол  равен углу
равен углу 
Найдём косинус угла KAC используя теорему косинусов:
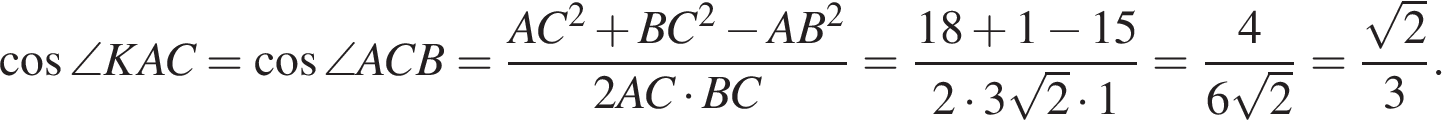
Ответ: 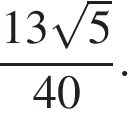
Источник: Банк заданий ФИПИ
25. Задание 25 № 311773. В остроугольном треугольнике ABC угол B равен 60°. Докажите, что точки A, C, центр описанной окружности треугольника ABC и точка пересечения высот треугольника ABC лежат на одной окружности.
Решение.
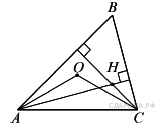
Обозначим центр описанной окружности треугольника ABC черезO, а точку пересечения высот через H. Тогда  и
и  Таким образом, точки A, C, O и H лежат на одной окружности.
Таким образом, точки A, C, O и H лежат на одной окружности.
Источник: МИОО: Диагностическая работа по математике 01.10.2013 вариант МА90101.
26. Задание 26 № 311704. Длина катета 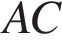 прямоугольного треугольника
прямоугольного треугольника 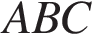 равна 3 см. Окружность с диаметром
равна 3 см. Окружность с диаметром 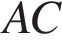 пересекает гипотенузу
пересекает гипотенузу 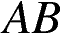 в точке
в точке 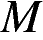 . Найдите площадь треугольника
. Найдите площадь треугольника 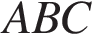 , если известно, что
, если известно, что 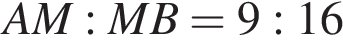 .
.






 Решение какого из данных неравенств изображено на рисунке?
Решение какого из данных неравенств изображено на рисунке? Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма. В окружности с центром в точке O проведены диаметры AD и BC, угол OAB равен 25°. Найдите величину угла OCD.
В окружности с центром в точке O проведены диаметры AD и BC, угол OAB равен 25°. Найдите величину угла OCD. На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах.
На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах.
 Дизайнер Павел получил заказ на декорирование чемодана цветной бумагой. По рисунку определите, сколько бумаги (в см2) необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность чемодана, если каждую грань он будет обклеивать отдельно (без загибов).
Дизайнер Павел получил заказ на декорирование чемодана цветной бумагой. По рисунку определите, сколько бумаги (в см2) необходимо закупить Павлу, чтобы оклеить всю внешнюю поверхность чемодана, если каждую грань он будет обклеивать отдельно (без загибов).












