Муниципальное общеобразовательное бюджетное учреждение
Увальская средняя общеобразовательная школа
Проект
«А площадь у Вас какая?»
предмет математика
Выполнила ученица 9 б класса Дьячук Наталья Андреевна
Руководитель проекта учитель математики Акинфиева
Татьяна Петровна
Отметка о результатах:
| Оценка | Количество баллов | Зачтено/незачтено |
|
|
|
|
| Уровень |
|
Члены комиссии:
2019-2020 учебный год
Оглавление
Введение…………………………………………………………………...…………...…2-3
Глава 1. История возникновения геометрии..............................................................4
1.1. Понятие геометрии……………………………………...…………………..4
1.2. Возникновение геометрии..........................................................................4
Глава 2. Треугольник..........................................................................................................5
2.1. Определение треугольника.........................................................................5
2.2. Виды треугольников………………………..………….…..….…..….…..6-7
Глава 3. Площадь треугольникa……………………………………………………….8
3.1. Понятие площади, единицы измерения..................................................8
3.2. Площадь равнобедренного треугольника..............................................9
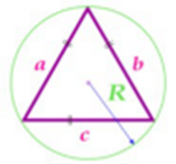
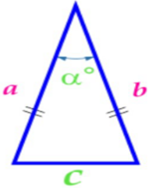
3.3. Площадь равностороннего треугольника……………………..………9
3.4. Площадь прямоугольного треугольника……………………...……….9
3.5. Площадь всех типов треугольников……………………………..……10
Заключение…………………………………………………………………………...……11
Список используемой литературы………………………………………………..…12
Приложение. Применение формул при решении задач
Введение
Геометрия обладает целым рядом качеств, располагает огромными возможностями для эмоционального и духовного развития человека. «Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Всё вокруг – геометрия». Эти слова, сказанные великим французским архитектором Ле Корбюзье в начале XX в., очень точно характеризуют и наше время. Мир, в котором мы живём, наполнен геометрией домов и улиц, гор и полей, творениями природы и человека. Лучше ориентироваться в нём, открывать новое, понимать красоту и мудрость окружающего мира помогает нам геометрия.
Начав подготовку к государственной итоговой аттестации по математике, я заметила, что в блок «Геометрия» включено много задач на вычисление площади треугольника. В курсе изучения геометрии основной школы мы рассмотрели основные формулы нахождения площади треугольника. Это формула Герона, нахождения площади треугольника через основание и высоту, проведенную к нему, через две стороны и синус угла между ними, через радиусы вписанной в треугольник окружности и описанной около него. Меня заинтересовал вопрос, можно ли использовать другие формулы при решении задач.
Я провела исследование, цель которого: определить, существуют ли другие способы нахождения площади треугольника.
Актуальность данной работы определяется тем, что знания и умения находить площадь треугольника имеют огромное значение для решения задач, в том числе и заданий единого государственного экзамена. Данное исследование, которое выходит за рамки нашей школьной программы, поможет найти новые подходы к решению геометрических задач.
Объект исследования: треугольник.
Предмет исследования: площадь треугольника.
Исследовательский метод определяется как самостоятельное решение проблемы с применением рассуждения, доказательства и анализа фактов.
В своих буклетах я разместила, интересные факты использования треугольника в разных областях жизни человека, постаралась показать, что данная геометрическая фигура окружает нас в повседневной жизни, в природе, что геометрия - прообраз красоты, поместила стихи о треугольнике.
Практическая значимость работы определяется возможностью использования данного материала при изучении тем «Треугольники», «Площадь треугольника», «Окружность, вписанная в треугольник», «окружность, описанная около треугольника» на уроках математики, при подготовке к государственной итоговой аттестации, а также на уроках географии, биологии, рисования и музыки.
Совместно с руководителем был разработан ход исследования:
1. Изучить теоретический материал учебника и дополнительных источников информации и найти новые способы нахождения площади треугольника.
2. Оформить результаты, сделать соответствующие выводы.
В ходе работы мне предстояло подтвердить или опровергнуть суждение о том, что существуют другие способы нахождения площади треугольника.
При работе над проектом я опиралась на материалы учебников «Геометрия 7-9», «Геометрия 10-11» для общеобразовательных организаций, авторы Л.С. Атанасян и др., пособий «История математики в школе: V-VIII; IX – X класс» Глейзера Г.И., интернет-источники (Википедия, сайты mnogoformul.ru, 100formul.ru, Яндекс. Кью и др.).
Глава 1. История возникновения геометрии
Геометрия зародилась в глубокой древности. Строя жилища и храмы, украшая их орнаментами, размечая землю, измеряя расстояния и площади, человек применял свои знания о форме, размерах и взаимном расположении предметов, он использовал свои геометрические знания, полученные из наблюдений и опытов. Почти все великие учёные древности и средних веков были выдающимися геометрами. Древнегреческий философ Платон одним из девизов своей школы провозгласил: «Не знающие геометрии не допускаются!»
В обычной жизни на каждом шагу мы встречаемся с понятием “площадь”. Что такое “площадь”, знает каждый. Каждый понимает смысл слов: площадь комнаты, площадь садового участка. Подумайте и самостоятельно ответьте на вопрос: что такое “площадь”? И вы увидите, что не так-то это просто. Даже математики смогли создать соответствующую математическую теорию сравнительно недавно. Правда, это никому не мешало успешно использовать понятие площади и в науке, и на практике с незапамятных времен. Измерение площадей считают одним из самых древних разделов геометрии; в частности название “геометрия” (т.е. “землемерие”) связывают именно с измерением площадей. Согласно легенде, эта наука возникла в Древнем Египте, где после каждого разлива Нила приходилось заново производить разметку участков, покрытых плодоносным илом, и вычисление их площадей. По-видимому, в древности приходилось рассматривать лишь участки, мало отличающиеся от прямоугольника по форме. Лишь в последствие было полностью развито учение о площадях и получены точные формулы для вычисления площади прямоугольника, параллелограмма, треугольника, трапеции и других многоугольников. Определение площадей геометрических фигур – одна из древнейших практических задач. Правильный подход к их решению был найден не сразу, но уже древние греки умели правильно находить площади многоугольников.
Глава 2. Треугольник
Среди множества различных геометрических фигур на плоскости выделяется большое семейство треугольников. Изображение треугольников и задачи на треугольники встречаются в египетских папирусах, которым более 4000 лет, в старинных индийских книгах и других древних документах. Уже тогда была известна теорема, получившая впоследствии название теоремы Пифагора, которая применялась для построения прямых углов на местности с помощью веревочного треугольника со сторонами 3, 4, 5 (египетский треугольник). Через 2000 лет в древней Греции учение о треугольнике достигает высокого уровня. Известны такие древнегреческие ученые, как Архимед, Пифагор, Фалес.
Учение о треугольнике развивалось в ионийской школе, основанной в VII веке до нашей эры Фалесом, затем в школе Пифагора. Древние греки решили упорядочить накопленные сведения о треугольнике и написали много трудов. Наиболее совершенной оказалась работа Евклида «Начала» (365-300 до н.э.).
Несколько тысячелетий геометры столь подробно изучили треугольник, что иногда говорят о «геометрии треугольника» как о самостоятельном разделе элементарной геометрии.
Изучая справочную литературу, я узнала, что определение слова «треугольник» в толковых словарях русского языка трактуется по-разному. В словаре Ожегова Сергея Ивановича «треугольник - это многоугольник с тремя углами, а также всякий предмет, устройство такой формы (прямоугольный треугольник, деревянный треугольник, солдатский треугольник); название сержантского и старшинского знака различия на петлицах в Красной Армии; в советском учреждении, на предприятии: совместно действующие три руководящих лица - администратор, секретарь партийной организации и председатель профсоюзного комитета (треугольник цеха)».
В словаре Ушакова Дмитрия Николаевича «треугольник – это геометрическая фигура, ограниченная тремя взаимно пересекающимися прямыми, образующими три внутренних угла (мат.) (тупоугольный треугольник, железный треугольник); ударный музыкальный инструмент из согнутого в форме такой фигуры стального прута, по которому ударяют металлической палочкой (муз); в учреждении, предприятии или их отделах - общее название для трех руководящих лиц: руководителя по административной линии и руководителей по линии партийной и профсоюзной работы (треугольник завода)».
А в словаре Ефремовой Татьяны Федоровны «треугольник - геометрическая фигура на плоскости, ограниченная тремя пересекающимися прямыми, образующими три внутренних угла (остроугольный треугольник); три человека (двое мужчин и одна женщина или две женщины и один мужчина), связанные любовными отношениями (любовный треугольник».
ВИДЫ ТРЕУГОЛЬНИКОВ
В зависимости от величин углов различают следующие виды треугольников:
| Название | Определение | Рисунок |
| Остроугольный | Треугольник, у которого все углы являются острыми. | 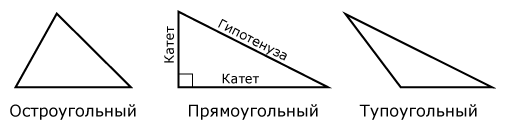 |
| Прямоугольный | Треугольник, у которого один из углов прямой. | 
|
| Тупоугольный | Треугольник, у которого один из углов тупой. |  |
В зависимости от соотношения длин сторон различают следующие виды треугольников:
| Название | Определение | Рисунок |
| Разносторонний | Треугольник, у которого все стороны имеют различную длину. | 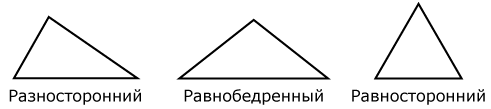 |
| Равнобедренный | Треугольник, у которого две его стороны равны между собой. Сторона, не равная двум другим, называется его основанием. |
 |
| Равносторонний | Треугольник, у которого все три его стороны равны между собой. |  |
Треугольник является одной из первых геометрических фигур, которая стала использоваться в орнаментах древних народов. Треугольник — символ триединой природы вселенной: Небо, Земля, Человек; отец, мать, дитя; человек как тело, душа и дух; мистическое число три; тройка, первая из плоских фигур. Отсюда символ поверхности вообще. Поверхность состоит из треугольников (Платон).
.
Глава 3. Площадь треугольника
Древнее землемеры выполняли геометрические построения, измеряли длины и площади; астрологии рассчитывали расположение небесных светил – всё это требовало весьма обширных познаний о свойствах плоских и пространственных фигур, и в первую очередь о треугольнике.
Площадь треугольника - это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной тремя отрезками (сторонами), которые соединяют три точки (вершины), не лежащие на одной прямой. Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
Квадратный метр, производная единица Международной системы единиц (СИ); 1 м² = 1 са (сантиар);
Квадратный километр, 1 км² = 1 000 000 м²; гектар, 1 га = 10 000 м²; ар (сотка), 1 а = 100 м²: квадратный дециметр, 100 дм² = 1 м²; квадратный сантиметр, 10 000 см² = 1 м²; квадратный миллиметр, 1 000 000 мм² = 1 м²; барн, 1 б = 10−28 м², и др.
Русские устаревшие: квадратная верста = 1,13806 км²; десятина = 10925,4 м²; копна = 0,1 десятины — сенные покосы мерили копнами; квадратная сажень = 4,55224 м².
Мерами земли при налоговых расчётах были выть, соха, обжа, размеры которых зависели от качества земли и социального положения владельца.
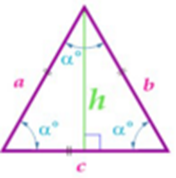
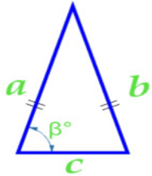
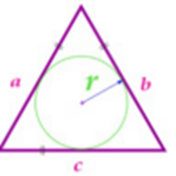
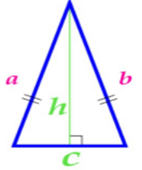
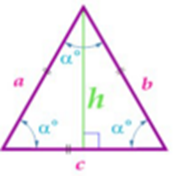
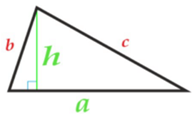
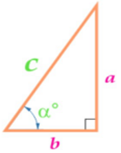
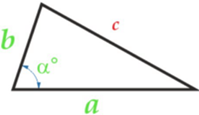
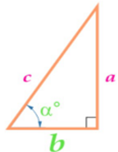
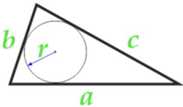
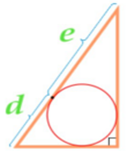
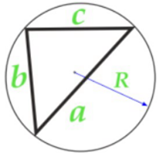
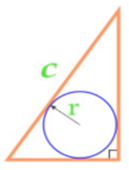
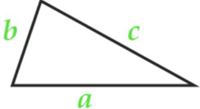
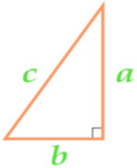
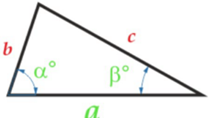
Изучая литературу, я сделала вывод, что все знакомые из курса математики основной школы и найденные мной в результате исследования формулы можно разделить на четыре группы. Это частные случаи: площадь равнобедренного треугольника, площадь равностороннего треугольника, площадь прямоугольного треугольника и общие формулы для всех типов треугольников. Эти формулы вы видите на слайдах презентации.
| Площадь равнобедренного треугольника | Площадь равностороннего треугольника |
| 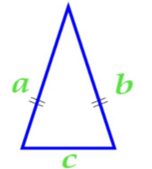 |
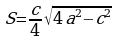 | 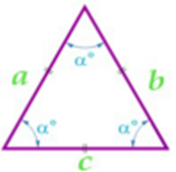 | 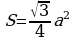 |
| 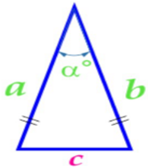 | 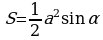 |  | 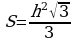 |
|  | 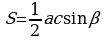 |  | 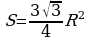 |
|  | 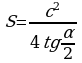 |  | 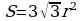 |
|  | 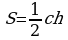 |  | 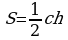 |
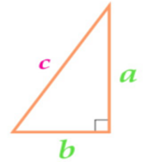
| Площадь прямоугольного треугольника | Площадь всех типов треугольников |
|  | 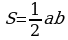 |  | 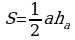 |
|  | 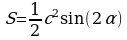 |  | 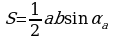 |
|  | 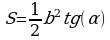 |  | 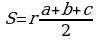 |
|  | 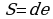 |  | 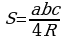 |
|  | 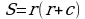 |  | 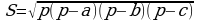 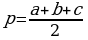 |
|  | 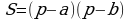 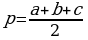 | 
| 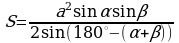 |
Заключение
Существует множество способов нахождения площади треугольника. При решении задач мы пользуемся наиболее удобным способом.
Формулы вычисления площади треугольника используются почти во всех сферах деятельности человека и с их помощью можно показать, что геометрия - прообраз красоты.
Умения применять различные способы для вычислений и расчетов необходимы каждому человеку, так как с треугольниками мы сталкиваемся в повседневной жизни постоянно.
Уметь грамотно проводить элементарные вычисления площадей треугольников должен каждый современный учащийся.
В моем проекте приведены общие формулы для всех типов треугольников, частные случаи для равносторонних, равнобедренных и прямоугольных треугольников. В зависимости от вида треугольника и его известных исходных данных, площадь треугольника можно вычислить по различным формулам.
Работая над проектом, я обобщила и углубила свои знания по данной теме. Перед написанием проекта я ставила перед собой задачи и, думаю, что мне удалось их разрешить. В практической части проекта мною было решено 14 задач, которые показались мне более сложными и интересными.
Я считаю, что эти навыки мне очень пригодятся при сдаче ОГЭ по математике, а также при изучении курса математики в старших классах. При написании проекта у меня возникали различные трудности, главная из которых - оформление проекта. Печатание текста и особенно задач с чертежами - очень кропотливая работа. Поэтому при его написании я развила не только свои математические способности, но и компьютерные знания в некоторых областях.
В дальнейшем я хотела бы продолжить работу над проектом, чтобы ещё более усовершенствовать навыки решения задач и знания теории.
Список используемой литературы:
1. Геометрия, 7-9:Учебник для общеобразовательных организаций. Авторы Л.С. Атанасян, В.Ф. Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина.-5-е издание Москва «Просвещение» 2015- 384с.
2. Геометрия, 10-11: Учебник для общеобразовательных организаций/ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – 15-е изд. – М: Просвещение 2015-206с.
3. Геометрия 7-9: Углубл, курс развивающего мат. образования / В. Г. Болтянский, Г. Д. Глейзер; Под ред. В. Г. Болтянского, 383 с. ил. 21 см, М. Ин-т учеб. "Пайдейя" 1998
4. Глейзер Г.И. История математики в школе: IX – X класс Пособие для учителей. – М.: Просвещение, 1983 – 351с
5. Глейзер Г.И. История математики в школе: VII – VIII класс Пособие для учителей. – М.: Просвещение, 1982 – 240с.
6. Зив Б.Г. Задачи к урокам геометрии 7-11 класс. – С. – Петербург, 1998 НПО «Мир и семья – 95»- 624с.
7. Игнатьев Е.И. В царстве смекалки / Под редакцией М.К. Потанова – 4-е изд. – М.: Наука 1984, 192с
8. Смирнова И.М. В мире многогранников: Кн. для учащихся / И. М. Смирнова. - М.: Просвещение, 1995. - 143 с.
9. Штейнгауз Г.Д. Математический калейдоскоп. - Москва - Ленинград: Гостехиздат, 1949
10. Штейнгауз Г.Д. Сто задач / Г. Штейнгауз; Пер. с польского Г. Ф. Боярской, Б. В. Боярского. - 3-е изд., стереотип. - М. : Наука, 1982. - 167 с. : ил.; 20 см.
11. Энциклопедический словарь юного математика/Сост. Э-68 А. П. Савин. - М.: Педагогика, 1989. - 352 с
Приложение
Применение формул при решении задач
Задача 1. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150. Боковая сторона треугольника равна 2. Найдите площадь этого треугольника.
Решение: площадь треугольника равна половине произведения двух его сторон, умноженного на синус угла между ними.
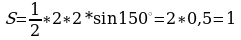 Ответ: 1.
Ответ: 1.
Задача 2. Две стороны равнобедренного треугольника равны 8 и 5 , а две его высоты равны 4,8 и 3. Найдите площадь треугольника.
Решение: 1 способ. По формуле Герона: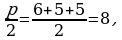
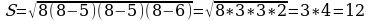 .
.
2 способ: проведем высоту к основанию. Т.к. треугольник равнобедренный, то высота является медианой, тогда из прямоугольного треугольника по т. Пифагора высота равна 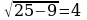 и
и 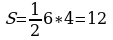
Ответ:12
Задача 3. Найдите площадь треугольника, изображенного на рисунке.
B
A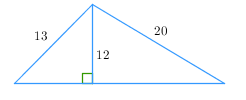 C
C
H
Решение: найдем площадь треугольника по формуле 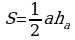 , где h=BH, a=AC=AH+HC. Треугольники ABH и CBH – прямоугольные.
, где h=BH, a=AC=AH+HC. Треугольники ABH и CBH – прямоугольные. 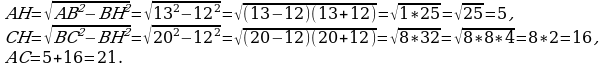
Получаем, 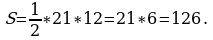 Ответ: 126
Ответ: 126
Задача 4. Чему равна площадь равностороннего треугольника, если радиус описанной окружности равен 5?
Решение: найдем площадь треугольника по формуле 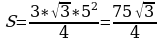 . Ответ:
. Ответ: 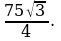
Задача 5. Чему равна площадь равностороннего треугольника, если радиус вписанной окружности равен 2?
Решение: найдем площадь треугольника по формуле 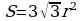 .
. 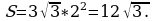 Ответ:
Ответ: 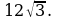
Задача 6. Высота равностороннего треугольника равна 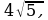 найдите его площадь.
найдите его площадь.
Решение: найдем площадь треугольника по формуле 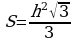 .
. 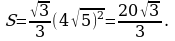 Ответ:
Ответ: 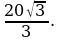
Задача 7. Сторона равностороннего треугольника равна 6см, найдите его площадь.
Решение: найдем площадь треугольника по формуле 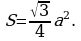
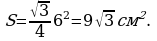 Ответ:
Ответ: 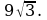
Задача 8. Известно, что стороны треугольника 5 см, 6 см и 8 см, а радиус описанной около треугольника окружности равен 4 см. Найдите его площадь.
Решение: по условию a = 5 см, b = 6 см, с = 8см, R = 4см, найдем площадь треугольника по формуле 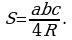
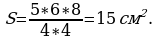 Ответ: 15.
Ответ: 15.
Задача 9. Периметр треугольника равен 48, одна из сторон равна 18, а радиус вписанной в него окружности равен 3. Найдите площадь этого треугольника.
Решение: площадь треугольника можно найти по формуле: S=1\2Pr, где P = 48 (периметр треугольника), r = 3 – радиус вписанной окружности. Получаем: S = 1/2*48*3 = 72 Ответ: 72.
Задача 10. Сторона равностороннего треугольника равна 20. Найдите его площадь, деленную на 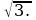
Решение: площадь треугольника находится по формуле:
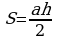 , где а – основание треугольника, h – высота, проведенная к этому основанию. Длина основания нам известна по условию – 10. Осталось найти высоту. Рассмотрим прямоугольный треугольник ABD (см. рис.), BD – высота. Известно, что в равностороннем треугольнике высота является и биссектрисой, и медианой, значит AD = DC = 5. Воспользуемся теоремой Пифагора и найдем сторону BD:
, где а – основание треугольника, h – высота, проведенная к этому основанию. Длина основания нам известна по условию – 10. Осталось найти высоту. Рассмотрим прямоугольный треугольник ABD (см. рис.), BD – высота. Известно, что в равностороннем треугольнике высота является и биссектрисой, и медианой, значит AD = DC = 5. Воспользуемся теоремой Пифагора и найдем сторону BD: 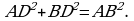
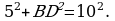
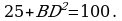
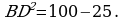
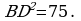
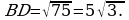 Теперь найдем площадь равностороннего треугольника ABC,
Теперь найдем площадь равностороннего треугольника ABC, 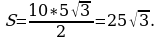 Разделим площадь на
Разделим площадь на 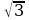 , получим
, получим 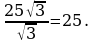 Ответ: 25.
Ответ: 25.
Задача 11. Высота равностороннего треугольника равна 15. Найдите его площадь, делённую на 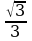 .
.
Решение: 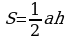 , где а - сторона, h – высота, и в то же время
, где а - сторона, h – высота, и в то же время 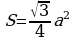 , следовательно
, следовательно 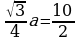 ,
, 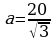 ,
, 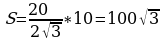 , а так как надо найти S, деленную на
, а так как надо найти S, деленную на 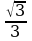 , получаем (100√3):(√3/3) = 300. Ответ: 300.
, получаем (100√3):(√3/3) = 300. Ответ: 300.
Задача 12. На клетчатой бумаге с клетками размером 1см×1см изображён треугольник. Найдите его S.
Решение: по формуле Пика 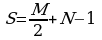 , где M – количество узлов на границе треугольника, N – количество узлов внутри треугольника («узлы» - точки пересечения линий). M = 3 (красные точки), N = 20 (зеленые точки)
, где M – количество узлов на границе треугольника, N – количество узлов внутри треугольника («узлы» - точки пересечения линий). M = 3 (красные точки), N = 20 (зеленые точки)
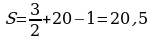 . Ответ: 20,5.
. Ответ: 20,5.


























Задача 13. Внутри параллелограмма ABCD выбрана произвольная точка и проведены отрезки PA, PB, PC. Площади трех из образовавшихся треугольников равны 1, 2 и 3. Какие значения может принимать площадь четвертого треугольника?
Р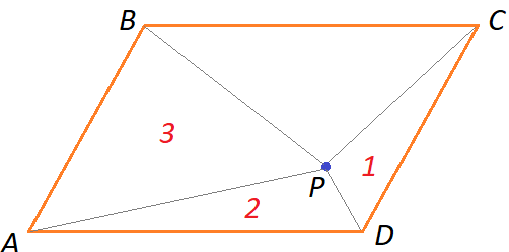 ешение: сделаем рисунок и обозначим площади, например, так:
ешение: сделаем рисунок и обозначим площади, например, так:
Тогда
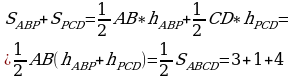
Необходимо, чтобы 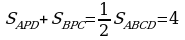 . Ответ: 4
. Ответ: 4
Если площади «распределены» по-другому,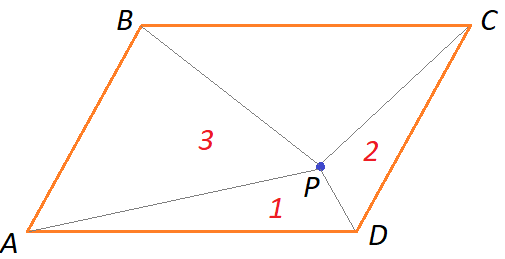 то
то 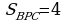 .
.
Ответ: 2 или 4.
Задача 14. В треугольнике одна из сторон равна 10, другая равна 12, а тангенс угла между ними равен 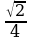 . Найдите площадь треугольника.
. Найдите площадь треугольника.
Решение:  В
В 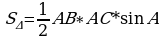 ,
,
C 1 + tg2 A = 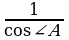 , 1 +
, 1 + 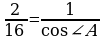 , cos2 A=
, cos2 A=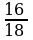
 12 10 т.к. sin2A + cos2 A = 1, sin A =
12 10 т.к. sin2A + cos2 A = 1, sin A = 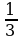 . Тогда
. Тогда
A 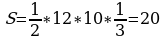 . Ответ: 20.
. Ответ: 20.
23










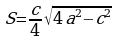

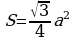

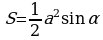

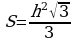

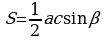

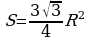

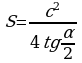

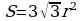

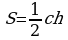


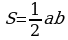

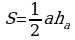

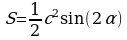

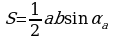

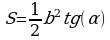

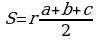

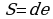

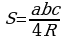

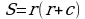

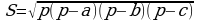
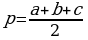

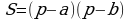

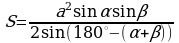
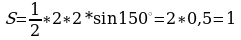 Ответ: 1.
Ответ: 1.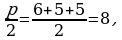
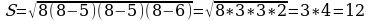 .
. 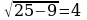 и
и 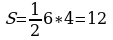
 C
C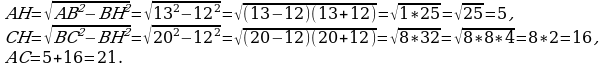
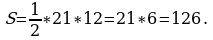 Ответ: 126
Ответ: 126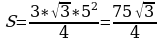 . Ответ:
. Ответ: 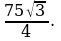
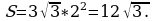 Ответ:
Ответ: 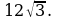
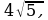 найдите его площадь.
найдите его площадь.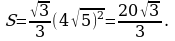 Ответ:
Ответ: 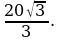
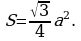
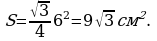 Ответ:
Ответ: 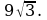
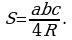
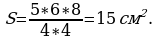 Ответ: 15.
Ответ: 15.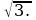
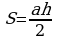 , где а – основание треугольника, h – высота, проведенная к этому основанию. Длина основания нам известна по условию – 10. Осталось найти высоту. Рассмотрим прямоугольный треугольник ABD (см. рис.), BD – высота. Известно, что в равностороннем треугольнике высота является и биссектрисой, и медианой, значит AD = DC = 5. Воспользуемся теоремой Пифагора и найдем сторону BD:
, где а – основание треугольника, h – высота, проведенная к этому основанию. Длина основания нам известна по условию – 10. Осталось найти высоту. Рассмотрим прямоугольный треугольник ABD (см. рис.), BD – высота. Известно, что в равностороннем треугольнике высота является и биссектрисой, и медианой, значит AD = DC = 5. Воспользуемся теоремой Пифагора и найдем сторону BD: 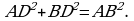
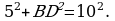
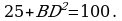
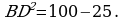
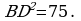
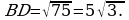 Теперь найдем площадь равностороннего треугольника ABC,
Теперь найдем площадь равностороннего треугольника ABC, 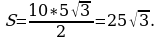 Разделим площадь на
Разделим площадь на 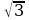 , получим
, получим 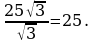 Ответ: 25.
Ответ: 25.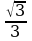 .
.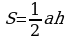 , где а - сторона, h – высота, и в то же время
, где а - сторона, h – высота, и в то же время 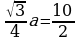 ,
, 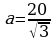 ,
, 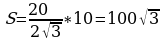 , а так как надо найти S, деленную на
, а так как надо найти S, деленную на 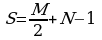 , где M – количество узлов на границе треугольника, N – количество узлов внутри треугольника («узлы» - точки пересечения линий). M = 3 (красные точки), N = 20 (зеленые точки)
, где M – количество узлов на границе треугольника, N – количество узлов внутри треугольника («узлы» - точки пересечения линий). M = 3 (красные точки), N = 20 (зеленые точки)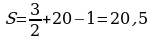 . Ответ: 20,5.
. Ответ: 20,5.




 ешение: сделаем рисунок и обозначим площади, например, так:
ешение: сделаем рисунок и обозначим площади, например, так: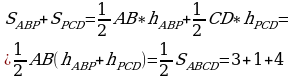
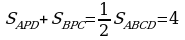 . Ответ: 4
. Ответ: 4 то
то 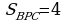 .
.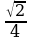 . Найдите площадь треугольника.
. Найдите площадь треугольника. В
В 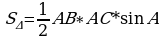 ,
, 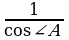 , 1 +
, 1 + 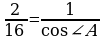 , cos2 A=
, cos2 A=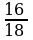
 12 10 т.к. sin2A + cos2 A = 1, sin A =
12 10 т.к. sin2A + cos2 A = 1, sin A = 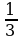 . Тогда
. Тогда 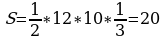 . Ответ: 20.
. Ответ: 20.









