Министерство образования и науки республики Бурятия
АМО «Еравнинский район»
Муниципальное бюджетное общеобразовательное учреждение
«Можайская средняя общеобразовательная школа»
Республиканская научно-практическая конференция
«Шаг в будущее»
Секция: Алгебра
Проект
«Математика и косы»
Авторы работы: Дондокова Аделина,
Цыбикова Аюна,
ученицы 9 класса
Руководитель: Кудрина Надежда
Андреевна,
учитель математики
с. Можайка ,2023 г.
Оглавление
Введение
Теоретическая часть:
1 Историческая справка.
2 . Теория кос
Практическая часть
Заключение
Список использованных источников информации
Приложение
1.Введение
Актуальность. Косы присутствуют в нашей жизни в различных видах и вариациях, но не все знают, что косы-это красивый геометрический объект. Чем отличается математическая коса от косы, которую практически каждый человек умеет заплетать из трех прядей волос? В начале нашего исследования мы изучили литературу, провели анализ источников информации по данной теме в сети «интернет» и пришли к выводу: красивое и наглядное понятие косы сейчас в центре внимание современной математики и физики. В основе нашей работы (её теоретической части) лежит статья «косы и узлы» а. Б. Сосинского, опубликованная в научно-популярном физико-математическом журнале «Квант» (1989) год, №2). Мы провели анкетирование среди школьников 5 – 11 классов и выяснили: ребята не подозревают, что коса – это ещё и математический объект. Изучив литературу и опираясь на результаты социологического исследование (анкетирование) определили следующую проблему.
Проблема. Плетение кос – разве это математика.
Гипотеза. Косы – один из простейших геометрических объектов, легко поддающихся классификации и «алгебраизации».
Цель. Установление взаимосвязи между плетением кос и математикой.
Задачи
Изучить теорию кос, историю возникновения и развития.
Рассмотреть классификацию и алгебраизацию кос
Научиться плести косы
Найти связь между математическими косами и косами в жизни
Рассмотреть положение кос
Предмет исследования. Косы
Объект исследования. Классификация и алгебраизация кос
Методы исследование. Теоретические, практические, математические
Практическая значимость. Материалы нашего исследования могут быть использованы:
для дальнейшего изучения инвариантов узлов
для повышения образовательного уровня школьников (в качестве дидактического материала для проведения: предметных декад, школьных конференций и т.д.)
на занятиях внеурочной деятельности.
Тезисы по тексту работы. Плетение кос – разве это математика? Косы – один из простейших геометрических объектов, легко поддающихся «алгебраизации». Теория кос – это реальная и живая наука. Теория кос и узлов – сравнительно молодой и интенсивно развивающийся раздел математики. Теория кос, основания которой были построены благодаря азарту и настойчивости немецкого алгебраиста Эмиля Артина, является красивым синтезом геометрии, алгебры и алгеометрических методов. Косы – один из простейших геометрических объектов, легко поддающийся «алгебраизации»: косы с одинаковым числом нитей можно умножать. Теория кос имеет много приложений жизни, как в математике, так и за пределами её Встречая косы в повседневной жизни, мы не подозревали, что это ещё и математические объекты. В нашей работе мы исследовали связь между плетением кос и математикой, рассмотрели классификацию и алгебраизацию кос. Нам удалось установить связь между красивыми топологическими объектами – косами и математикой с помощью основной теоремы о косах.
2. Теоретическая часть
1 . Историческая справка. Теория кос – это реальная и живая наука. Теория кос и узлов – сравнительно молодой и интенсивно развивающийся раздел математики. Математики впервые заинтересовались косами и узлами лишь в ⅩⅠⅩ веке и с того времени теория кос и узлов обрела статус самостоятельного раздела математики. Теория кос, основание которой были построены благодаря азарту и настойчивости немецкого алгебраиста Эмиля Артина, является красивым синтезом геометрии, алгебры и алгоритмических методов. (приложение 1). Первоначально косы были предложены Артином в качестве математической модели для текстильной промышленности, но приложения этой теории оказались весьма разнообразными. Теперь они занимают важное место в комплексном анализе, комбинаторике, квантовой механике и квантовой теории поля. В последние 20 лет математики и физики с огромным интересом стали заниматься соответствующими теориями (особенно, теорией узлов). Среди лауреатов Филдсовской премии есть советские и российские математики: Сергей Новиков (1970), Григорий Маргулис (1978), Владимир Дринфельд (1990), Ефим Зельманов (1994), Максим Концевич (1998), Владимир Воеводский (2002), Григорий Перельман (2006, от медали отказался), Андрей Окуньков (2006) и Станислав Смирнов (2010).
2 . Теория косОпределение. Косу можно себе представить так: в верхний и нижний край вертикальной доски вбито по n гвоздиков (n может равняться 1,2,3,4...) – каждый из гвоздиков верхнего основания соединён нитью с одним из гвоздиков нижнего; нити попарно не пересекаются и всё время должны опускаться вниз (нить не имеет права, повернувшись, начать подниматься вверх). По прибытии вниз мы находим те же нити (также зафиксированные гвоздями), но не обязательно в том же порядке. Касательный вектор в любой точке кривой должен всё время «смотреть вниз», ему запрещается быть горизонтальным и тем более «смотреть вверх».
Классификация кос. Наше исследование начнём с примеров кос.
Среди кос выделяются:

Девичья коса – символ девичества, молодости, красоты, чистоты. В Древней Руси девушки берегли косу до замужества. С древнейших времен длинные волосы считаются символом красоты и женственности.
 Коса, все нити которой вертикальные прямые, называется тривиальной.
Коса, все нити которой вертикальные прямые, называется тривиальной.
Тривиальная коса – частый случай крашеной косы.
 Крашенная коса К3
Крашенная коса К3
Крашеной называется любая коса, которая отвечает тождественная перестановка (1 2 1 2 3…? 3…?), т.е. коса, сохраняющая порядок номеров нитей.
 Циклическая коса К4
Циклическая коса К4
Среди кос следует выделить, кроме крашенных, в известном смысле противоположные им – циклические косы: это косы, переставляющие все номера нитей по единому циклу, как это делаете коса К4: 12 4 3 1.
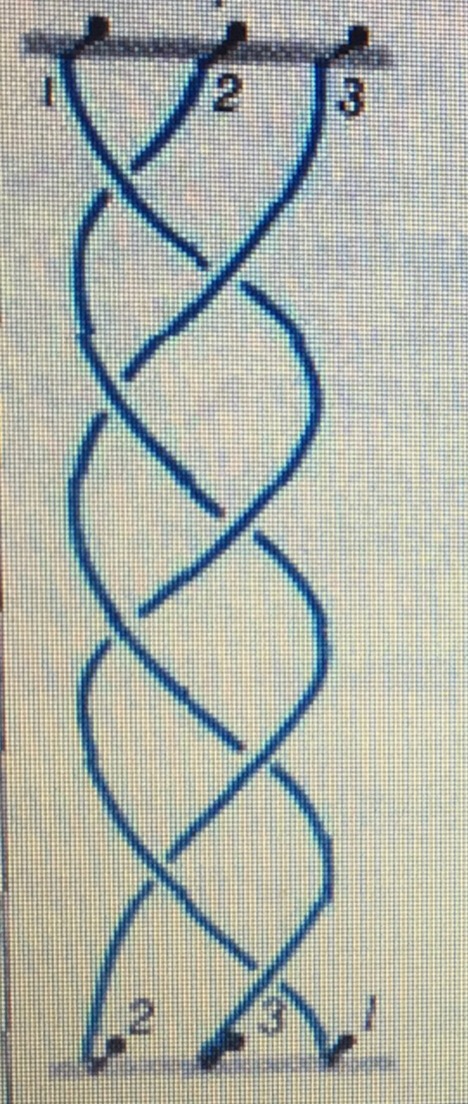
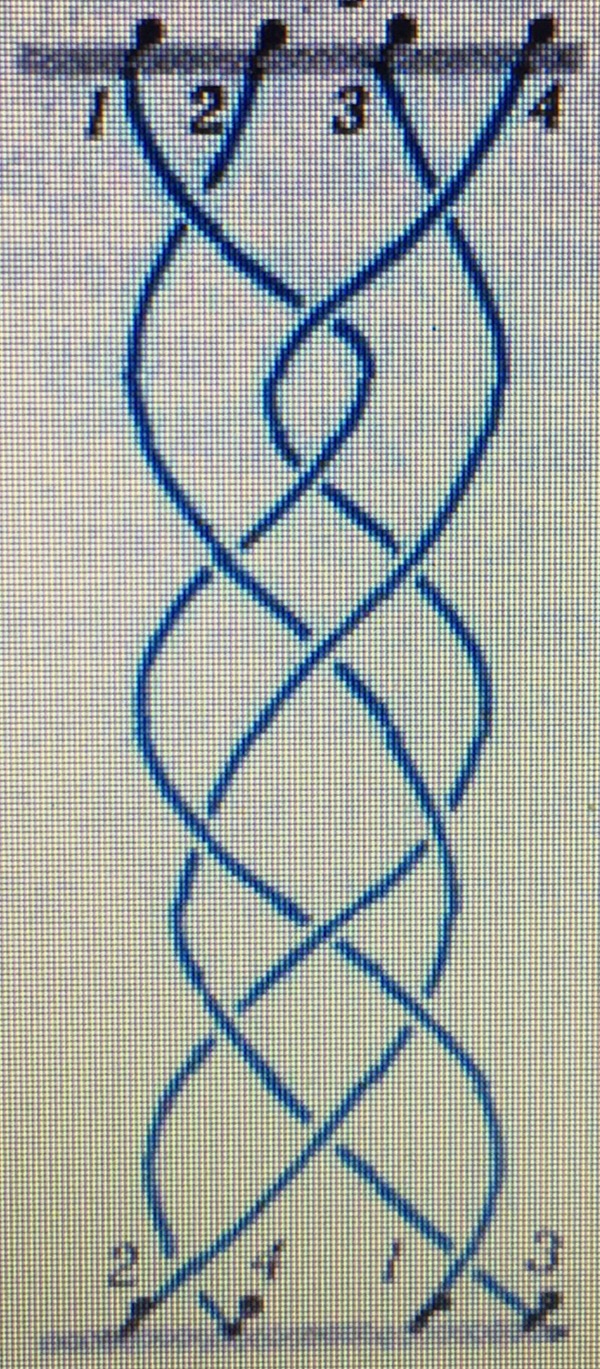
В таблице (рисунок 1) представлены проекции кос на плоскость из трех и четырех нитей. (Приложение 1)
Две косы считаются эквивалентными (т.е. Одинаковым), если одну можно превратить в точную копию другой, двигая нити (без разрывов и склеивание) так, чтобы точка каждой нити перемещались только в горизонтальной плоскости. Такое движение показано на рисунке 3. (Приложение 1)
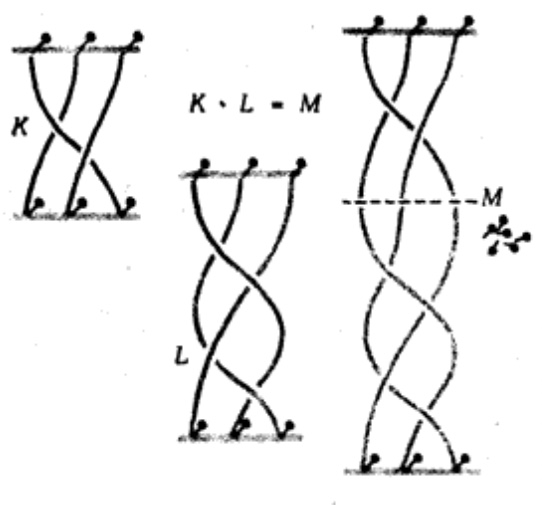
Алгебраизация кос. Косы - один из простейших геометрических объектов, легко поддающийся «алгебраизации»: косы с одинаковым числом нитей можно умножать. Делается это совсем просто (рисунок 3): нужно приложить одну косу к другой, склеив соответствующие нити, и удалить ставшие ненужными гвоздики (нижние гвозди первой косы, верхние – второй). В таблице (рис.4) представлена проекция умножения кос на плоскость из трёх нитей. (приложение 1)
2.4. Определение. Возьмём две косы a и b с одинаковым числом нитей и соединим нижние концы нитей первой косы с верхними концами нитей второй косы рис. 4; полученную косу, сжатую в два раза в вертикальном направлении, называют произведением этих двух кос и обозначают ab.
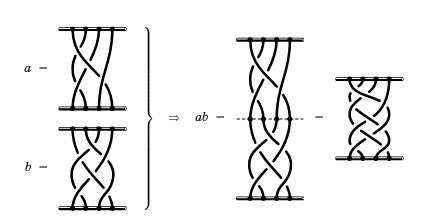
Провели данное определение в практике.
Такое умножение обладает рядом свойства обычного умножения чисел.
Подведем итог в виде теоремы.
2.5. Теорема о косах. Свойства умножения кос
Ассоциативный закон (сочетательный). Общий у кос и у чисел К1(К2К3) =(К1К2) К3
Наличие единицы. Тривиальная коса К2 = 1, для которой 1K = K1= K
Т.е. Коса, которая, как число 1, не изменяет то, что на неё умножается.
Наличие обратного элемента (аналог деления). У каждой косы К имеется обратная коса
Как построить обратную косу? Очень просто: нужно зеркально отразить К относительно горизонтальной плоскости. Рассмотрим данную операцию на рисунке 5. (приложение 1) Всякий раз, когда некоторое множество снабжено операцией, обладающей тремя свойствами, о которых мы только что упоминали, математики говорят, что они имеют дело с группой. Итак, мы только что показали, что множество кос с n нитями образует группу. Эту группу обозначают Кₙ. Отметим сразу же, что группа кос Кₙ (для n2) – в отличии от чисел – не обладает переместительным свойством: произведение двух кос зависит в общем случае от порядка множителей. Один из вопросов анкетирования звучал так: «Каждую ли косу можно расплести? (Рисунок 6а).
Теорема (для кос с любым числом прядей больше двух)
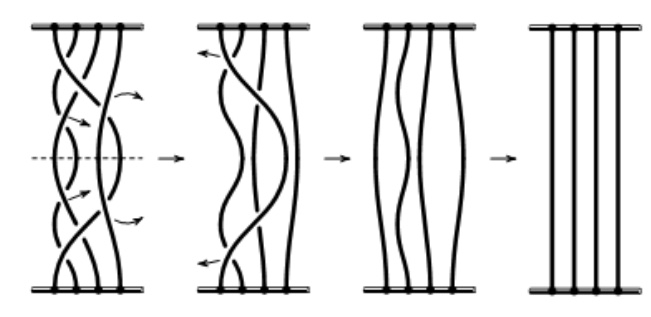
Все косы, полученные четным числом вращений подвески (причем допустимы вращения в любых направлениях) можно расплести. Косы, полученные нечетным числом полных оборотов, расплести нельзя.
Вывод: косу «склеенную» из двух симметричных, можно «расплести» приложение (рис. 6а, 6б, 6в). Достаточно ли соотношений I – III для доказательства всех равенств в теории кос? Оказывается – да: немецкий математик Эмиль Артин, создатель теории кос, доказал в 1936 году, что любое равенство в теории кос вытекает из соотношений I – III. Эта замечательная теорема позволяет решить основную проблему теории кос – проблему классификации. Именно, можно указать (бесконечный) список кос (без повторений) и алгоритм, относящий любой косе её номер в этом списке.
3.Приложение кос.
Астрономия
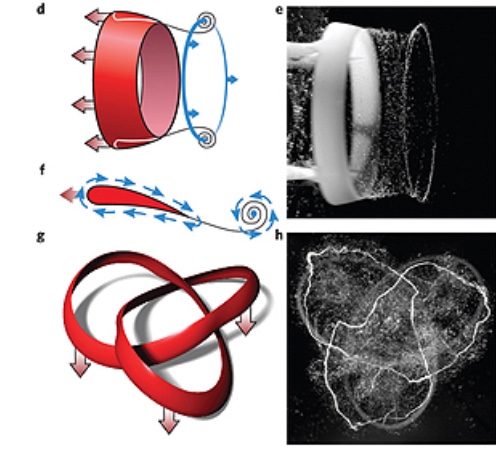
Теория кос имеет большое значение для изучения Солнца. Недавно ученые установили, что на Солнце перенос энергии от поверхности к короне может быть опосредован особыми торнадо, сплетающимися в косы.
Физика
Физикам из Университета Чикаго впервые удалось создать в лаборатории узел из вихря воды и наблюдать за его эволюцией и распадом. В результате, ученым удалось рассмотреть, как образуются, движутся и распадаются узлы, образованные движением жидкости.
 География
География
Коса образуется в результате перемещения обломочного материала волнами и вдольбереговыми течениями и отложения этих наносов в результате огибания потоком наносов выступа берега.
Биология
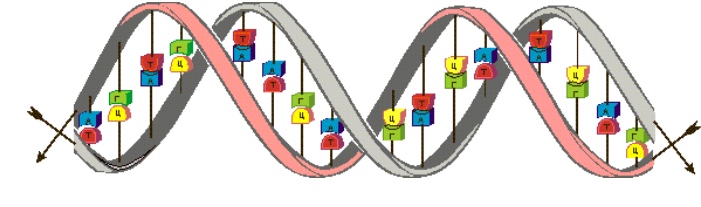
Молекула ДНК.
Её молекулы имеют огромную по молекулярным масштабам длину и состоят из двух нитей, сплетённых между собой в двойную спираль.
3.Практическая часть
Анкетирование. Анкетирование проводилось среди учащихся 5 – 11 классов нашей школы. 46 учащихся ответили на следующие вопросы анкеты.
Вопросы анкеты
Что такое косы?
Какие виды кос вы знаете?
В каких областях применяются косы?
Каждую ли косу можно расплести?
Цель проведения анкеты – установить, что ребятам известно о косах; предполагают ли они, что косы являются также и математическими объектами.
Результаты анкетирования занесли в таблицу (Приложение 3)
В результате проведенного социологического исследования получены следующие результаты:
Оказалось, что большинство опрошенных имеют представление о косах, как о причёске или хозяйственном инструменте, с помощью которого косят траву.
Из числа участников анкетирования лишь 3(6%) человека смогли определить косу как некоторый объект (в таблице ответы выделены цветом).
На вопрос о классификации кос, большинство респондентов снова дали ответы, связанные с внешним видом человека.
Среди ответов мы определили для себя группу оригинальных, редких.
Мы пришли к выводу о том, что ребята не воспринимают косу как математический объект. Классификацию кос соотносят с внешним видом человека (причёска) или хозяйственным инструментом. Однако все опрошенные соотносят косы с их плетением.
Выполняя исследовательскую работу, мы изучили виды кос и научились их плести.
Среди кос выделяются:
Девичья коса – символ девичества, молодости, красоты.
Тривиальная коса – частный случай крашеной косы.
Коса, сохраняющая порядок номеров нитей.
Циклические косы – косы, противоположные крашеным.
Вывод: оказалось, достаточно сложно сплести циклическую косу и косу, состоящую из пяти нитей, умножать косы - это совсем просто. Нужно приложить одну косу к другой, склеив соответствующие нити, и удалить ставшие ненужными гвоздики (нижние гвозди первой косы, верхние – второй). Проведя исследование по данной теме, мы изучили математическое понятие «коса», историю возникновения и развития, а также классификацию кос и их свойства. Нами было рассмотрено приложение кос в различных сферах жизни и деятельности человека. В ходе исследования нам удалось установить связь между плетением кос и математикой. Встречая косы в повседневной жизни, мы не подозревали, что это ещё и математические объекты. По красоте теория кос не уступает классической математике, которая изучается в школе.
Заключение
В нашей работе мы исследовали связь между плетением кос и математикой. В работе мы рассмотрели классификацию и алгебраизацию кос. Коса – это формальная модель того, что понимается под словом «сплетение» в обычной жизни (девичья коса, плетёный брелок, классический канат из переплетённых жил и т.д.), т.е. множество нитей, запутанных некоторым определённым образом. Нам удалось установить связь между красивыми топологическими объектами косами и математикой с помощью основной теоремы о косах. Мы показали, что множество кос с n нитями образует группу. Установили, что группа кос Кn (для n2) – в отличии от чисел – не обладает переместительным свойством. Гипотеза о том, что косы – один из простейших геометрических объектов, легко поддающихся классификации и «алгебраизации», нашла своё подтверждение. В своей работе мы показали практическое применение данной темы.
Список использованных источников информации
Косы и узлы/ [А. Б. Сосинский]. – М.: Квант №4, 1973
Узлы и косы / [А. Б. Сосинский]. – М.: МЦНМО, 2001
Узлы. Хронология одной математической теории / [А. Б. Сосинский]. – М.: МЦНМО, 2005
Узлы. Хронология одной математической теории / [А. Б. Сосинский]. – М.: Квант №3, 2009
Цикл лекций в Летней школе «Современная математика» / [А. Б. Сосинский].- http://www.mathnet.ru/php/presentation.phtml?option_lang=rus&presentid=220
http://sinsam.kirsoft.com.ru/KSNews_327.htm
http://genius.pstu.ru/file.php/1/pupils_works_2012/Kovyev_Nikita.pdf
http://www.findpatent.ru/patent/206/2061245
 Приложение №1
Приложение №1
Эмиль Артин (1898-1962 г. г.).
| К1 | К2 | К3 | К4 |
| «Девичья коса» | Тривиальная коса | Крашенная коса | Циклическая коса
|
| 
| 
| 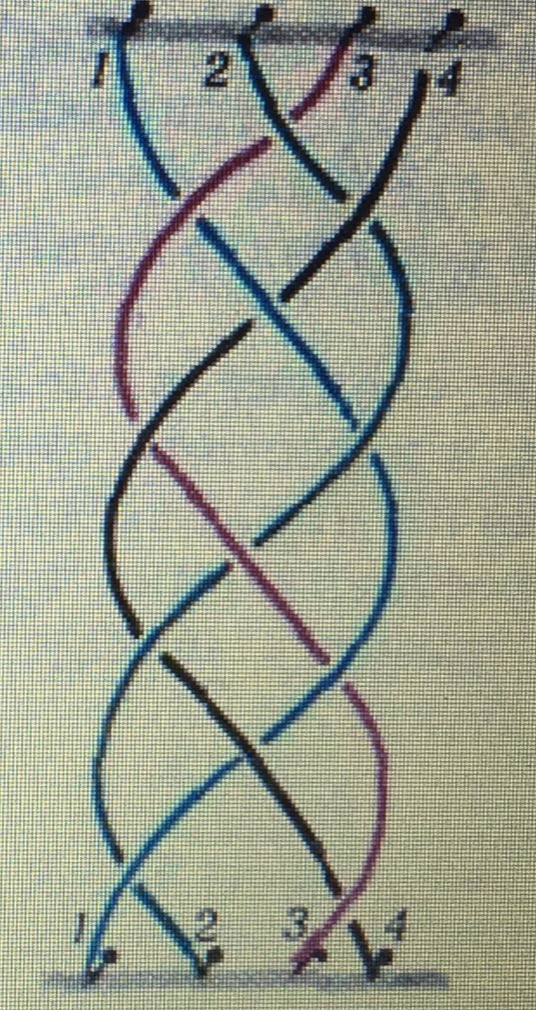
| 
|
На рисунке - вверху у начала каждой нити указан ее порядковый номер. Внизу снова указан номер каждой нити.
Приложение №2
В данной таблице (рис. 3) представлено геометрическое доказательство
тривиальности косы.
В таблице (рис.4) представлена проекция умножения кос на плоскость из трёх нитей.
| 
|
| M = K*L |
Приложение №3
В таблице (рис. 5) показано как на плоскости выполняется построение обратной косы.
Приложение №4
Результаты анкетирования
| Что такое косы? | Какие виды кос вы знаете? | В каких областях применяются косы? | Каждую ли косу можно распутать? |
| Популярные ответы |
| - Заплетённые волосы -Хозяйственный инструмент
| -Колосок -Рыбий хвост -Простая -Сложная -Не знаю - «Ёлочка» -Дреды -красивые | -Чтобы траву косить -Парикмахерский зал -В сельском хозяйстве
| -Нет -Да -Не каждую -Любую
|
| Редкие ответы |
| -Знал бы, если читал много -Коса – географический объект -Косы - это ремесленный инструмент, чтобы выкашивать траву и многие виды злаков -Косы – это переплетённые нити, веревка, канат, жгут -Коса – сплетение чего-либо | -Французская
| -В области красоты -Для опрятного вида на работе и в школе -В науке -В жизни
|
|
| Оригинальные ответы |
| Коса от слова cos (косинус) Коса – это такие штуки, в которые заплетаются какие-нибудь штуки | «Я мужик!!! Никакие!!!» |
|
|
Приложение №5
Рыбий хвост
 Обратная коса
Обратная коса

Калачик

Простая









 Коса, все нити которой вертикальные прямые, называется тривиальной.
Коса, все нити которой вертикальные прямые, называется тривиальной. Крашенная коса К3
Крашенная коса К3 Циклическая коса К4
Циклическая коса К4 

 География
География
 Приложение №1
Приложение №1

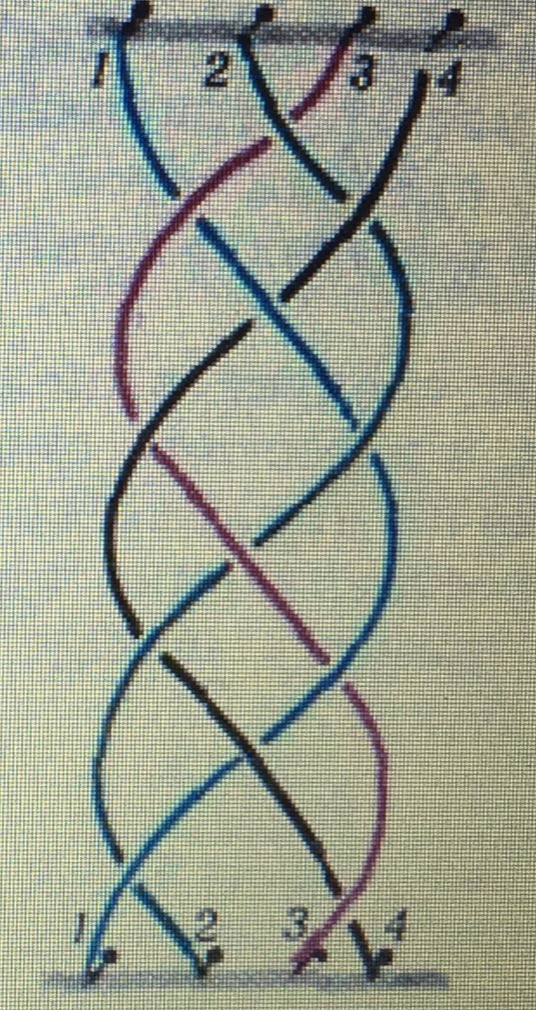







 Обратная коса
Обратная коса












