Муниципальное общеобразовательное учреждение
Малодубенская средняя общеобразовательная школа №7
Итоговый проект по геометрии
Тема: «Неизвестный дельтоид»
Обучающейся 9 класса
Романовой Ирины Александровны
Руководитель проекта:
учитель математики
Романова Людмила Геннадьевна
г.о. Орехово-Зуево
2019 г.
Оглавление
Введение 3
Определение. 4
Свойства. 4
Первое свойство. 4
Второе свойство. 4
Третье свойство. 5
Четвертое свойство. 5
Пятое свойство. 5
Признаки. 6
Первый признак. 6
Второй признак. 6
Площадь дельтоида. 7
Первая формула. 7
Вторая формула. 7
Третья формула. 8
Четвертая формула. 8
Окружность, вписанная в дельтоид. 9
Окружность, описанная около дельтоида. 9
Теорема 1. 9
Теорема 2. 10
Теорема 3. 10
Примеры решения задач. 11
Задача 1. 11
Задача 2. 11
Задача 3. 12
Задача 4. 12
Заключение. 13
Список используемой литературы. 14
Введение
Существуют различные виды классификаций четырехугольников, например, по параллельности сторон выделяют параллелограмм, у которого попарно параллельны все стороны, и трапецию - параллельны две стороны, по равенству сторон выделяют ромб и квадрат, по равенству всех углов – квадрат и прямоугольник и т.д., эти фигуры изучаются в школьной программе.
Изучая литературу, решая геометрические задачи, я обратила внимание на то, что четырехугольник, у которого диагонали перпендикулярны, но не является ромбом, обладает рядом интересных свойств. Этот четырехугольник – дельтоид.
В своем классе я провела опрос по определению геометрических фигур: трапеция, параллелограмм, ромб и дельтоид. Участие приняли 25 человек. Результаты опроса отображены на диаграмме.
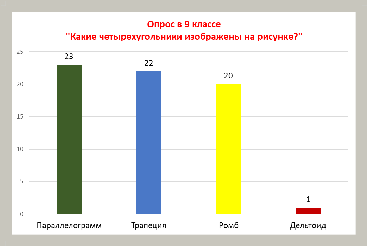
Поэтому целью моего проекта является: изучить дельтоид и рассмотреть применение его в окружающем мире.
Для выполнение этой цели были поставлены следующие задачи:
Дать определение дельтоида.
Изучить свойства и признаки дельтоида.
Рассмотреть задачи, которые решаются с дельтоидом.
Найти практическое применение.
Определение.
Дельтоид – четырехугольник, обладающий двумя парами смежных сторон одинаковой длины, диагонали пересекаются под прямым углом. Дельтоид иначе называют ромбоидом. Название дельтоид происходит от названия греческой буквы (дельта).
| 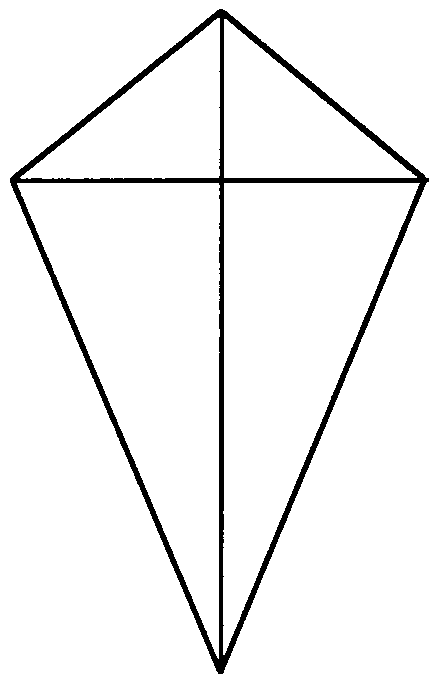
Выпуклый дельтоид |
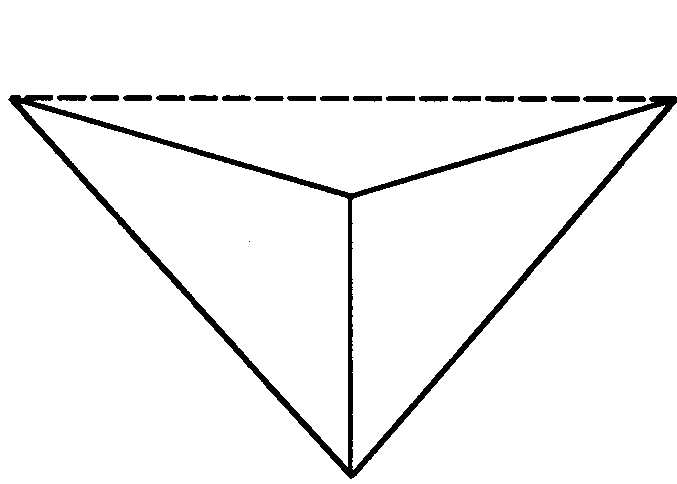
Невыпуклый дельтоид |
Свойства.
Первое свойство.
У дельтоида одна пара противолежащих углов равна. (Углы, лежащие по разные стороны от главной диагонали равны.)
| 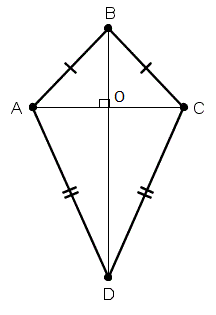
| Дано: ABCD – дельтоид Доказать: /BAD = /BCD Решение: ∆ABC –равнобедренный, AC - основание, Значит /BAC = /BCA ∆ADC –равнобедренный, AC - основание, Значит /CAD = /ACD /BAD = /BAC + /DAC /BCD = /BCA + /DCA Значит /BAD = /BCD
|
Второе свойство.
Большая диагональ является биссектрисой.
| 
| Дано: ABCD – дельтоид Доказать: BD – биссектриса Док-во: 1) ∆BAD = ∆BCD (по 1 призн), т.к. AB = CB, AD = CD, /BAD = /BCD 2) /ABD = /CBD /ADB = /CDB 3) BD – биссектриса. |
Третье свойство.
Диагонали дельтоида пересекаются, и точкой пересечения меньшая диагональ делится пополам.
| 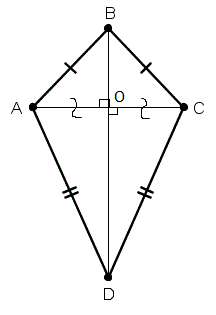
| Дано: ABCD – дельтоид Доказать: AO=CO Док-во: 1) т.к. ∆BAD = ∆BCD (аналогично в 1 свойству) 2) AO – высота ∆BAD, CO – высота ∆BCD (диагонали BD┴AC) 3) высоты равных треугольников тоже равны AO=CO
|
Четвертое свойство.
Осью симметрии дельтоида является большая диагональ.
| 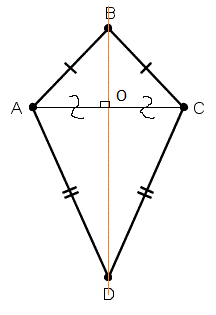
| Дано: ABCD – дельтоид Доказать: BD – ось симметрии Док-во: 1) рассмотрим симметрию относительно BD. 2) точка D перейдет в саму себя. 3) точка A перейдет в точку C, т.к. AO = OC и BD|AC 4) точка B перейдет в саму себя 5) точка C перейдет в точку A, т.к. AO = OC и BD|AC 6) ∆BAD перейдет в ∆BCD 7) BADC - BCDA |
Пятое свойство.
Параллелограммом Вариньона, построенный в серединах сторон дельтоида, является прямоугольник.
| 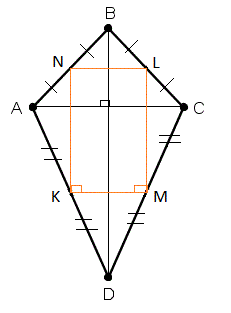
| Дано: ABCD – дельтоид Найти: определить вид четырехугольника KLMN Решение: 1) рассмотрим ∆BAD, KN - средняя линия, KN||BD, KN=1\2BD. 2) рассмотрим ∆BCD, LM - средняя линия, LM||BD, LM=1\2BD.
3) KN||LM, KN=LM. 4) так как BD|AC, то KN|NL, LM|KM. 5) KLMN- прямоугольник |
Признаки. Первый признак.
Теорема 1. Если одна из диагоналей четырехугольника является биссектрисой одного из его углов и делит периметр четырехугольника пополам, то четырехугольник есть дельтоид.
| 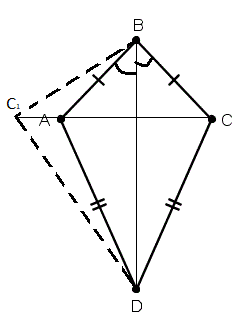
| Дано: ABCD - четырехугольник BD - биссектриса /ABD PBCD=PBAD Доказать: ABCD - дельтоид |
Доказательство: (от противного)
Предположим, что A и C – не симметричны, относительно BD.
Построим C1, симметричную точке C (C1 = A).
Так как периметры равны, т.е. PBCD=PBAC=PBC1D, то приходим к противоречию. Значит A-C1
ABCD – дельтоид.
Второй признак.
Теорема 2. Если у четырехугольна, вписанного в окружность, ось симметрии совпадает с диагональю, то он является дельтоидом.
| 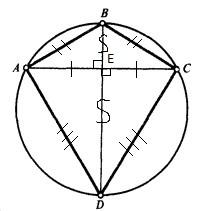
| Дано: ABCD - четырехугольник Окружность (O, R) – описанная BD – диагональ = ось симметрии Доказать: ABCD - дельтоид |
Доказательство:
Т.к. BD - ось симметрии, то A-C, значит AC-BD
∆ABE = ∆CBE (по 1 признаку: AE=CE, BE – общая, /BEA=/BEC=90), значит AB=BC
∆AED = ∆CED (по 1 признаку: AE=CE, DE – общая, /AED=/CED=90), значит AD=CD
ABCD – дельтоид
Площадь дельтоида. Первая формула.
S= 1/2d1d2
| 
| BD=d1, AC=d2. S=SABO+SCBO+SADO+SCDO SABO= 1/2AO*BO SCBO= 1/2BO*CO SADO= 1/2AO*DO SCDO= 1/2CO*DO S= 1/2AO*BO + 1/2BO*CO + 1/2AO*DO + 1/2CO*DO= =1/2BO(AO+CO)+1/2BO*AC+1/2DO*AC= =1/2AC(BO+DO)= 1/2AC*BD=1/2d1*d2 |
Вторая формула.
Известным индийским математиком Брахмагуптой (около 598 года н.э.) было установлена формула площади вписанного в окружность четырехугольника, а именно:
S=√(p-a)(p-b)(p-c)(p-d), где p=(a+b+c+d)/2 – полупериметр четырехугольника. Эта формула является обобщенным случаем известной формулы площади треугольника.
Применим данную формулу для вписанного в окружность дельтоида. Так как a=b и c=d получаем, что S=(p-a)(p-b). Докажем это.
S=(p-a)(p-b) или S=ab, т.к. P=(2a+2b)/2=a+b.
| 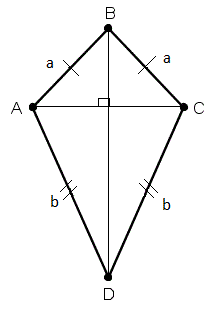
| 1) По теореме косинусов AC2= a2+ a2-2a2 *cos /B= = b2+ b2-2b2 *cos /D. AC2= 2a2+ 2a2-2a2 *cos /B= 2b2+ 2b2-2b2 *cos /D. 2) Т.к. ABCD – вписанный четырехугольник, то /D=1800-/B, поэтому cos /D= -cos /B, sin /D=sin /B, следовательно, 2a2-2a2 *cos /B= 2b2-2b2 *cos /D. 2(a2-b2) = 2cos /B(a2+b2) a2-b2 = (a2+b2) cos /B (1) Площадь четырехугольника равна сумме площадей треугольников, на который он разбивается своей диагональю, то есть S = 1/2*a2*sin /B+1/2*b2*sin /D = ½ (a2 + b2) sin /B или 2S = (a2 + b2) sin /B (2) Возведем неравенства (1) и (2) в квадрат и сложим их, учитывая, что cos2 /B + sin2 /B = 1, получим 4S2 + (a2 - b2)2 = (a2 + b2)2 4S2 = (a2 + b2)2 - (a2 - b2)2 4S2 = (a2 + b2 - a2 + b2) (a2 + b2 + a2 - b2) 4S2 = 2a2 * 2b2 S2 = a2 * b2 S = ab Это доказательство проводилось по рассуждениям древнего математика Брахмагупты, эту же формулу можно вывести короче:
|
Т.к. дельтоид вписан в окружность, то большая диагональ является диаметром, значит она разбивает четырехугольник на два равных прямоугольных треугольника (вписанный угол, опирающийся на диаметр равен 90⸰). Площадь прямоугольного треугольника равна S=1\2ab, значит площадь дельтоида равна S=ab.
Третья формула.
Площадь вписанного дельтоида можно найти другим способом. Докажем теорему: если дельтоид со сторонами a, b, вписан в окружность радиуса R, то его площадь равна
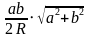
Доказательство:
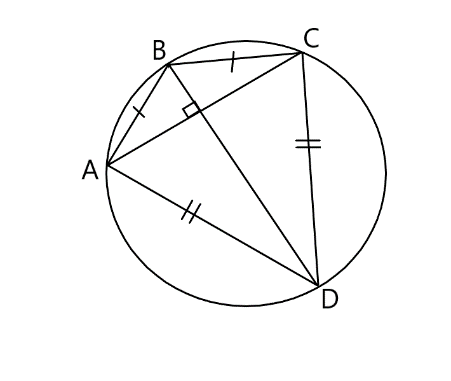
Пусть диагонали дельтоида равны x и y.
SABCD = SABC + SACD или SABCD = SBCD + SABD.
Воспользовавшись формулой S= abc/4R, где a,b,c, - стороны треугольника, а R- радиус описанной окружности, получаем:
SABCD = abx/2R (1) или SABCD = a2y/4R+ b2y/4R (2)
Перемножив неравенства (1) и (2), получаем:
SABCD = abx/2R*(a2y/4R+ b2y/4R) = 1/8R2* ab(a2+b2) * xy = 1/8R2* 2a2b2(a2 + b2) = 1/4R2* a2b2(a2 + b2) (так как по теореме Птолемея xy = ac+bd, то есть xy = 2ab), значит S = 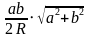 .
.
Четвертая формула.
Площадь параллелограмма Вариньона равна половине площади дельтоида.
| 
| Докажем, что SKLMN=1\2SABCD SABCD=1\2d1*d2 SKLMN= KL*LM=1\2d1*1\2d2= 1\2 SABCD, так как KL – средняя линия треугольника ABC и LM – средняя линия треугольника BCD. |
Окружность, вписанная в дельтоид.
Докажем, что в дельтоид можно вписать окружность.
Доказательство:
| 
| В четырехугольник можно вписать окружность, если суммы противолежащих сторон равны. Действительно, т.к. AB=BC и CD=AD, то AB+CD=BC+AD. |
Окружность, описанная около дельтоида.
Теорема 1.
В дельтоиде ABCD через точку пересечения диагоналей проведена прямая, перпендикулярная к одной из сторон. Доказать, что если эта прямая делит другую сторону пополам, то дельтоид можно вписать в окружность.
| 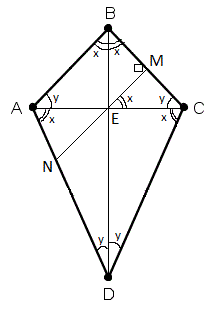
| Доказательство: Пусто прямая NM пересекает сторонe BC под прямым углом, а сторону AD делит пополам. Тогда /EMB=/MEC=/NAE, а это значит, что утверждение доказано. ABC/2x+2y=180 /ABC+/ADC=/BAD+/BCD= 2x+2y=180⸰ |
Утверждение: если четырехугольник является вписанным, то центр описанной около него окружности – точка пересечения серединных перпендикуляров к сторонам четырехугольника.
В самом деле, серединный перпендикуляр к отрезку содержит все точки, равно удаленные от концов этого отрезка, следовательно, точка пересечения серединных перпендикуляров вписанного в окружность четырехугольника, равно удалена от вершин этого четырехугольника, т.е. от некоторых точек окружности.
По определению центра окружности, из этого следует, что данная точка – центр описанной около этого четырехугольника окружности.
Теорема 2.
Вписанный дельтоид является примером гармонического четырехугольника (вписанный четырехугольник с перпендикулярными диагоналями, произведение длин противоположенных сторон которого равны)
Вписанный в окружность четырехугольник обладает рядом интереснейших свойств. Одно из них было доказано древнегреческим математиком и астрономом Клавдием Птолемеем (около 100 – 178 г. н. э.) в его знаменитом сочинении «Альмагест» (астрономы в странах арабского Востока называли эту книгу «Альмаджисти» - «Величайшие», отсюда и происходит её название «Альмагест»).
Теорема, носящая имя Птолемея: произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон.
| 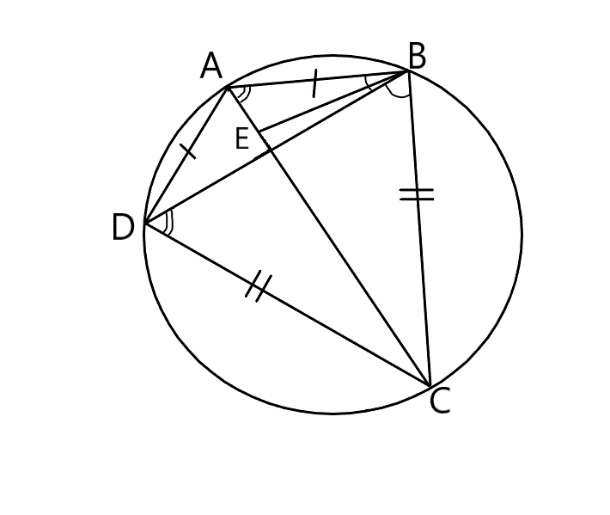
| Т.к. у дельтоида две пары равных соседних сторон, то утверждение выглядит так: d1*d2=2a*b
Докажем это: |
Возьмём на диагонали AC точку E так, что /ABE = /DBC. Тогда ∆ABE и ∆DBC подобны, т.к. /BAE = /BAC= /BDC. Поэтому 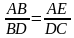 , т.е. AB*DC = AE*DB. (1) Ясно также, что /CBE = /DBA (т.к. /CBE = /DBC + /DBE (по условию)), а значит, ∆CBE и ∆DBA подобны, т.к. /BCE = /BDA (опираются на одну дугу), поэтому
, т.е. AB*DC = AE*DB. (1) Ясно также, что /CBE = /DBA (т.к. /CBE = /DBC + /DBE (по условию)), а значит, ∆CBE и ∆DBA подобны, т.к. /BCE = /BDA (опираются на одну дугу), поэтому 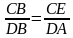 , то есть CB*DA = CE*DB (2). Сложив полученные неравенства (1) и (2), получим: AB*DC + CB*DA = AE*DB + CE*DB = DB*(AE + CE) = BD*AC,
, то есть CB*DA = CE*DB (2). Сложив полученные неравенства (1) и (2), получим: AB*DC + CB*DA = AE*DB + CE*DB = DB*(AE + CE) = BD*AC,
то есть d1*d2 = 2a*b
Теорема доказана.
Теорема 3.
Сумма квадратов неравных сторон равна учетверённому квадрату радиуса описанной окружности.
| Докажем его. 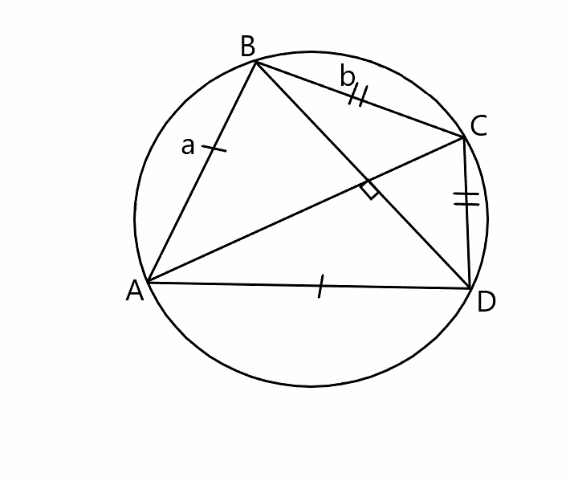
| Рассмотрим вписанный в окружность четырехугольник ABCD, диагонали которого перпендикулярны. В нём AB=a, BC=b, CD=c, AD=a, а радиус описанной окружности равен R. Докажем, что 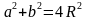 . . Обозначим BD как d1, AC как d2, /ABD как /1, /BAC как /2, /CAD как /3, /ADB как /4, тогда /BCA=/4 ( т.к. опирается с /ADB на одну дугу), аналогично /BCA=/4, /CBD=/3, /BDC=/2, /ACD=/1. По теореме синусов получаем: 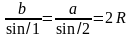 a = 2R*sin /2, b = 2R*sin /1 (так как /2 = 90⸰ - /1), из этого a2 + b2 = 4R2 sin /1 + 4R2 cos /1 = 4R2, следовательно, a2 + b2 = 4R2 Свойство доказано. |
Примеры решения задач.
Выше мы рассмотрели общие свойства дельтоида. Также свойства некоторых особых видов таких четырехугольников.
Теперь решим несколько задач, в которых встречается данный четырехугольник.
Задача 1.
В дельтоиде средние линии пересекаются на оси симметрии дельтоида.
| 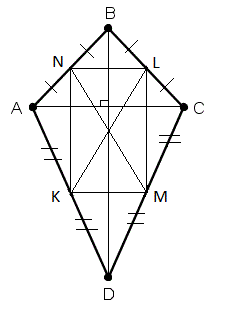
| Доказательство: Пусть K, L, M, N – середины сторон дельтоида. Поскольку KLMN – прямоугольник, то его диагонали пересекаются на оси симметрии BD. |
Задача 2.
В дельтоид вписана окружность, которая касается равных сторон в точках M и N, P и Q. Определить вид четырехугольника MNPQ.
| | Решение: Пусть ABCD - данный четырехугольник. Поскольку BM=BN, то MN||AC. Аналогично QP||AC. Поскольку QM=NP, то четырехугольник – равнобедренная трапеция. |
Задача 3.
Построить дельтоид ABCD по сторонам a, b и углу между равными сторонами y.
| | План построения: Построить произвольную прямую. Взять на ней точку D. Отложить от точки в данную полуплоскость угол y. Разделить угол пополам (т.к. у дельтоида диагональ является биссектрисой). Провести Окр (D, a), которая пересечет стороны угла в точках A и C. Провести Окр (A, b), которая пересечет биссектрису угла y в точке B. ABCD - данный четырехугольник. |
Задача 4.
Найдите площадь дельтоида ABCD, у которого AB=a, AD=b, AC=d.
| 
| Решение: Т.к. диагональ AC делится точкой пересечения диагоналей пополам, то AO=1/2d Из треугольника AOB:BO=  Из треугольника AOD:DO=  BD= Т.к. S=1\2d1*d2 получаем S=1\2d1*( ) |
Заключение.
В данной работе было рассмотрено что такое дельтоид, какими свойствами должен обладать четырехугольник, чтобы его можно было назвать дельтоидом. В заключении работы было разобрано несколько задач.
Но это далеко не всё, что может быть изучено по теме «Дельтоид».
Если посмотреть на карту неба, то мы можем обнаружить знакомую нам фигуру. Четыре самые яркие образуют ромбоид – характерную геометрическую фигуру созвездия Весы. В окружающем мире дельтоид встречается в конструировании воздушных змеев и летательных аппаратов, плавательных судов, а также в области биологии: крона дерева туя, лист березы, тело рыбы, форма носа, соединенные пальцы человека и др.
В качестве направлений для дальнейших исследований проект предполагает рассмотреть свойства аналогичных фигур и в стереометрии.
Расширить представленную в проекте тему можно изучением применения свойств дельтоида в оригами (Оригами – наглядная модель евклидовой геометрии)
Список используемой литературы.
Журнал «Квант» №2, 1992 г. http://kvant.mccme.ru/1992/02/p37.htm
Журнал «Квант» №10, 1991 г. http://kvant.mccme.ru/1991/10/p48.htm
И.Л. Никольская «Факультативны курс математике 7-9».
В.В. Прасолов «Задачи по планиметрии».
И.Ф. Шарыгин «Геометрия (планиметрия) 7-9».
В.А. Гусев, В.Н. Литвиненко, А.Г. Мордкович «Практикум по элементарной математике (геометрия)».
Картинка дельтоид https://yandex.ru/images/search















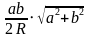



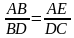 , т.е. AB*DC = AE*DB. (1) Ясно также, что /CBE = /DBA (т.к. /CBE = /DBC + /DBE (по условию)), а значит, ∆CBE и ∆DBA подобны, т.к. /BCE = /BDA (опираются на одну дугу), поэтому
, т.е. AB*DC = AE*DB. (1) Ясно также, что /CBE = /DBA (т.к. /CBE = /DBC + /DBE (по условию)), а значит, ∆CBE и ∆DBA подобны, т.к. /BCE = /BDA (опираются на одну дугу), поэтому 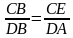 , то есть CB*DA = CE*DB (2). Сложив полученные неравенства (1) и (2), получим: AB*DC + CB*DA = AE*DB + CE*DB = DB*(AE + CE) = BD*AC,
, то есть CB*DA = CE*DB (2). Сложив полученные неравенства (1) и (2), получим: AB*DC + CB*DA = AE*DB + CE*DB = DB*(AE + CE) = BD*AC, 
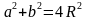 .
.