Проект по математике "Математика в школьных предметах"

Муниципальное казенное общеобразовательное учреждение 
«Кастореснкаясредняя общеобразовательная щкола №1» 
Касторенского района Курской области 

Индивидуальный итоговый проект

 
на тему «Математика в школьных предметах» 

по дисциплине «математика»

Обучающаяся: Виноградова Елизавета

9 «Б» класс 

Руководитель проекта :Вторникова Т.Н

(учитель математики) 

Касторное 2018 

Содержание

ВВЕДЕНИЕ 
ГЛАВА I . ПОНЯТИЕ О МАТЕМАТИКЕ КАК О НАУКЕ 
§1 Значение математики. …………………………………………..4-5
§2 Взаимосвязь с другими школьными предметами…………….5-9
ГЛАВА II.
§1 Взаимосвязь математики с литературой ……………………………..9-11
§2 Взаимосвязь математики с русским языком …………………………11-12
§3 Взаимосвязь математики с географией ………………………………..12-13
§4 Взаимосвязь математики с историей…………………………………..13-14

§5 Взаимосвязь математики с биологией……………………………….14-15
ГЛАВА III 
§1 Роль математики в современной науке ……………………......15-16

§2  Математика в жизни…………………………………………….16
§3 Диаграмма ……………………………………………………….17
Заключение………………………………………………..18
Список используемой литературы……………………………..19

Введение

Мы слышали много различных мнений по этому поводу. Некоторые уверены в том, что математика является царицей наук, некоторые, что математика – служанка, которая верно обслуживает различные науки. Задумавшись над этим вопросом, мы выбрала тему исследовательской работы « Математика в школьных предметах», поставила себе цель:выяснить, является ли математика царицей всех наук, показав связь математики с другими науками, значимость математики в жизни человека.

Честно говоря, я думала, что математика не играет уж такую великую роль в жизни людей, но когда начала делать проект и задумываться на эту тему, оказалось, что я была не права. О таком большом значении и важности математики в жизни людей я и не догадывалась. 
Тяжело представить, но когда-то люди совсем не умели считать! 
Факты убедительно свидетельствуют о том, что счет возник раньше, чем названия чисел

Обозначенная цель требует решение следующих задач:

1. Собрать материалы и изучить литературу по данной теме;

2. Раскрыть связь математики с другими школьными предметами, обозначив роль математики в жизни человека;

В своей работе мы выдвинули следующие гипотезы:

• математика – одна из самых важных наук;

• математика помогает в жизни человека;

Актуальность: проект даст возможность понять , что математика –царица всех наук

Значение математики

Название "математика" происходит от греческого слова "матейн" (mathein) - учиться, познавать. Древние греки вообще считали, что понятия "математика" (mathematike) и "наука", "познание" (mathema) - синонимы. Им было свойственно такое понимание универсализма этой отрасли знания, которое два тысячелетия спустя выразил Рене Декарт, писавший: "К области математики относят науки, в которых рассматриваются либо порядок, либо мера, и совершенно не существенно, будут ли это числа, фигуры, звезды, звуки или что-нибудь другое...; таким образом, должна существовать некая общая наука, объясняющая все, относящееся к порядку и мере, не входя в исследование никаких частных предметов. Другое объяснение происхождения слова "математика" связано с греческим словом "матема" (mathema), что означает урожай, сбор урожая. Разметка земельных участков (геометрия), определение сроков полевых работ (на основе астрономических наблюдений и вычислений), подготовка необходимого количества посевных материалов и подсчет собранного урожая требовали серьезных математических знаний .Многие часто задаются вопросом зачем нужна математика?. Нередко сам факт того, что эта дисциплина входит в обязательную программу университетов и школ, ставит людей в недоумение. Это недоумение выражается в следующем: Мол, для чего мне, человеку чья будущая (или нынешняя) профессия не будет связана с ведением расчетов и применением математическихметодов, знать математику? 
Человек пользовался окружавшими его однотипными предметами: пальцы, камешки, узелки, нарисованные на стене черточки, зарубки на палках и на деревьях, кучки камней и т.п. При возникновении языка слова связываются только с теми понятиями, которые уже существуют, т. е. распознаются. Слова "один", "два" и, возможно, "три" появляются независимо от счета. Счисление (нумерация) - совокупность приёмов наименования и обозначения чисел. Когда счет становится распространенным и привычным делом, для наиболее часто встречающихся (т. е. небольших) групп стандартных предметов возникают и словесные обозначения

С усложнением хозяйственной деятельности людей понадобилось вести счет в более обширных пределах, что потребовало создания более сложных счётных устройств. Это различные счёты (абак, соробан, суан-пан и т.п.) и позднее в средние века появляются механические счетные. Во многом благодаря математике цивилизация стала такой, какая она есть сейчас: развитой, высокотехнологичной, образованной и обеспеченной.Математическая наука позволила развиться цивилизации во всех ее аспектах.

Взаимосвязь математики с другими учебными предметами

Уже более двухсот лет прошло с тех пор, как химия перестала быть описанной наукой. После того, как гениальный М.В Ломоносов ввёл в химическую практику весы, знание математики стало необходимым для каждого химика. Ещё в 1741 г. М.В. Ломоносов в своём сочинение «Элементы математической химии» писал: ..если математики из сопоставления многих линий выводят многие истины, то и для химиков я не вижу и никакой иной причины, вследствие которой они не могли бы вывести большие закономерности из такого обличия имеющихся опытов, кроме незнания математики». Химик – технолог наших дней в своей практической работе повседневно использует огромный аппарат всех своих разделов высшей математики. Роль математики как важнейшего инструмента химии особенно возросла с развитием физической химии, химической тернодинамики и кинематики, теории расчётов химической аппаратуры и других новых областей химической науки.

Связь математики с литературой 

Многие считают, что математика сухая наука, которая совершенно не сочетается с литературой. Но ведь именно математика подарила нам такие слова как гармония, симметрия, пропорция. Каждому искусству присуще стремление к стройности, соразмерности, гармонии. Природа совершенна и у нее есть свои законы, выраженные с помощью математики и проявляющиеся во всех искусствах. Ведь недаром Карл Фридрих Гаусс назвал математику царицей всех наук. Математика и литература не так далеки друг от друга, как многие думают.

Искусство и наука требуют фантазии, творческой смелости, зоркости в наблюдении за различными явлениями жизни. Писатель должен видеть то, чего не видят другие, видеть глубже других. А математик преследует те же цели. 
Многие писатели и поэты обращались к математике как к наглядному сравнению ее с окружающим миром. А многие математики известны как замечательные писатели и некоторые из них приобрели широкую известность за счет своих литературных произведений. Как известно великий русский писатель Лев Николаевич Толстой организовал в своем имении Ясная поляна школу для крестьянских детей и сам преподавал в ней. Для своих учеников он написал и издал «Азбуку», в которой есть раздел «Арифметика». Поэты сравнивают природу с геометрическими фигурами и стихотворение сразу же играет новыми красками и представление становится более четким и понятным. Поэт Библус-РавилРаисович Бухарев, который закончил механико- математический факультет Казанскогоуниверситета и аспирантуру МГУ по кибернетике в своем стихотворении «Геометрия трав» нашел фигуры планиметрии практически на альпийском лугу. 

Математик, несбывшийся странник, 
Оглянись, удивляясь стократ: 
В травах — срез чабреца — пятигранник 
А в сеченье душицы — квадрат. 
Все на свете покажется внове 
Под гольцом, чья вершина в снегу 
Водосбор — треуголен в основе 
На цветущем альпийском лугу! 
Где же круг? Возле иглистой розы, Там, где луг поднебесный скалист, 
Вижу, с ветром играет березы 
Треугольно-ромбический лист.

Авторы, употребляя в своих произведениях математические термины, не просто так дают готовые знания и выдают математические секреты, а предлагают подумать, дают пищу для размышления. Но мы ведь можем рассматривать и литературные произведения с математической точки зрения. 

Если музыка - гармоническое упорядочение звуков, то поэзия - гармоническое упорядочение речи. Четкий ритм, закономерное чередование ударных и безударных слогов, упорядоченная размерность стихотворений, их эмоциональная насыщенность делают поэзию родной сестрой музыкальных произведений. Золотое сечение в поэзии в первую очередь проявляется как наличие определенного момента стихотворения в строке (кульминации, смыслового перелома, главной мысли произведения) , приходящейся на точку деления общего числа строк стихотворения в золотой пропорции. Так, если стихотворение содержит 100 строк, то первая точка Золотого сечения приходится на 62-ю строку (62%), вторая - на 38-ю (38%) и т.д. Исследования показали, что размеры стихов распределены весьма неравномерно. Поэты предпочитают размеры в 5, 8, 13, 21, 34 строки, то есть числа Фибоначчи.

Связь математики с русским языком 

Учение великого Пифагора целиком основывается на мысли о том, что

числа правят миром. Можно продолжить эту идею: не только числа сами

по себе, но и числовые закономерности, связи. Числа – это не

только обозначения количества или номеров при исчислении, числа –

это порядок, развитие памяти и различных операций с ними. Числа – это

даты исторических событий, без которых невозможно восприятие и

изучение истории.

Это экономика, хозяйствование, практически вся наука. Числа – космос, музыка, стихосложение, архитектура, символы, то есть целостная система окружающей нас действительности [1].Закономерно то, что русский язык – один из высокоразвитых языков мира – тесно и глубоко связан с математикой. Дело не только в целой системе числительных, математических терминах и понятиях, но и в традиционных математических «инструментах», представлениях .

Математика разнообразно проявляется в мире фразеологизмов, включающих в свой состав числительные. Фразеологизмом называется устойчивое сочетание слов данного языка, значение которого по отдельности не определяется значениями слов, входящих в его структуру. Примеры: Один на один. Одного поля ягода. На один манер (покрой). Раз-два - и готово. В два счёта. Раз-два и обчёлся. Бог троицу любит. В три ручья (плакать). Заблудиться в трёх соснах. За тридевять земель. Сидеть в четырёх стенах. С пятого на десятое. Седьмая вода на киселе. Семь пятниц на неделе. Семеро одного не ждут. На седьмом небе. Семь вёрст до небес и всё лесом. Девятый вал. Во сто крат и т.д.Сейчас редко можно встретить старинные русские меры длины. А в пословицах и поговорках они сохраняются: верста, сажень, аршин, локоть, пядь, вершок. Ты от правды на пядень, а она от тебя – на сажень (1 пядь - 1/12 сажени). За семь вёрст комара искали, а комар - на носу (1 верста = 1,1 км). У него в голове ни ползолотника (1 золотник - 4,3 грамма) [8]. Полено к полену – сажень. Не уступить ни пяди. Каждый купец на свой аршин меряет. От горшка два вершка, а уже указчик. Семи пядей во лбу. 
Числительные встречаются во многих загадках русского языка: Двенадцать братьев друг за другом бродят, друг друга не обходят.

Два брюшка, четыре ушка. Сто один брат в один ряд вместе связаны стоят. Четыре братца под одним шатром стоят, одним поясом связаны. Два братца в воду глядятся, век не сойдутся. Два близнеца – два братца верхом на нос садятся. Таких загадок существует огромное количество. Это свидетельствует о роли числовых обозначений, связей в картине мира человека. Впервые на использование «математического языка» в русских загадках, пословицах, поговорках обратил внимание Владимир Иванович

Даль, современник Пушкина и Гоголя [3]. 

Многое в структуре произведений поэзии делает этот вид искусства похожим на музыку. Каждый стих обладает своей музыкальной формой - своей ритмикой и мелодией. В строении стихотворений проявляются некоторые черты музыкальных композиций, закономерности музыкальной гармонии, а следовательно, и золотая пропорция, и числа Фибоначчи. Числа Фибоначчи - элементы числовой последовательности 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597... . Суть последовательности Фибоначчи, в том, что начиная с 0 или 1, следующее число получается сложением двух предыдущих. Если какой-либо член этой последовательности разделить предшествующий ему (например 13:8), результатом будет величина, колеблющаяся около иррационального значения.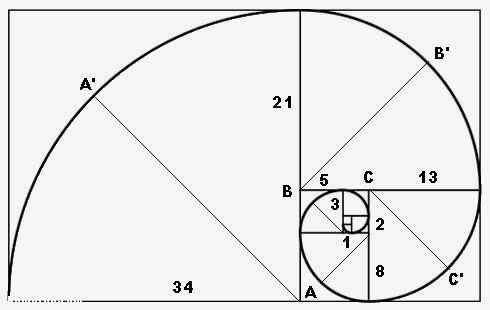

Связь математики с географией

Отношения между математикой и географией можно назвать очень близкими. Так, научить человека пользоваться географической картой или планом местности без элементарных математических знаний и навыков невозможно. Связь математики с географией проявляется всуществовании так называемых географических задач. Это задания: на определение расстояний по карте; на определение масштаба; на вычисление высоты горы по температурным градиентам или градиентам давления; на расчеты по демографическим показателям и тому подобное. Кроме этого, география в своих исследованиях очень часто использует математические методы: статистический, корреляционный, балансовый, метод моделирования (в том числе компьютерного) и другие. Если же говорить о экономической географии, то математику и вовсе можно смело назвать её "сводной сестрой".

Математика используется в географии при: вычислении количества жителей населённых пунктов (например: Москва – 10,5 млн.человек) определении масштаба (например: масштаб карты – 1: ) вычислении плотности населения (например: средняя плотность населения в Европе – 65.4 чел на 1 кв.км) измерении высоты гор (например: г. Эльбрус – 5642 м) при использовании широты и долготы; при нахождении геогр.объекта при помощи широты и долготы (например: координаты Москвы - 55°45 с. ш., 37°37 в. д.) при вычислении площади государств, городов (например: площадь Санкт-Петербурга – 3267,5 чел. на 1 кв.км). Также математика используется в географии при других вычислениях и нахождениях. Вернуться к задаче Если бы математика тесно не сотрудничала с географией, география вообще как наука не смогла бы развиваться. Доказательствами к этому являются такие факты: 1)Многие географические термины позаимствованы из математики 2)В географии используются простейшие основы математики 3)Все законы физики и химии сформировались в какой-то мере благодаря математике, а географии химические и физические законы помогают развиваться и занимать своё место в науках. 

Связь математики с историей 

Карл Фридрих Гаусс-это немецкий математик (1777-1855), великий ученый, которого при жизни называли королём математиков, отличался удивительной способность быстро и неутомимо вычислять ( например найти все простые числа меньше 3000000 затратив на это 750 часов).

Одни задачи имеют очень солидный возраст, исчисляются тысячелетиями, другие – сравнительно молоды – им всего лишь несколько веков или даже десятилетия. История многих задач драматична, овеяна тайнами и легендами. Но все эти задачи замечательны тем, что в процессе их решения появились новые математические понятия, новые области математики. С решением задач связаны имена великих математиков. Поэтому решение или просто чтение исторических задач расширяет кругозор учащихся, развивает их речь и память, решение задач требует определённого упорства, напряжения, развивает хорошие качества у учеников – трудолюбие, любознательность, активность, целеустремлённость.

Основное математическое понятие это «число». Интерес к изучению чисел возник у людей в далёкой древности. И вызван он был не только практической необходимостью. Привлекала необычайное, магическая сила числа, которым можно выразить количество любых предметов.

Достаточно совершенные формы записи чисел были созданы ещё за два тысячелетия до новой эры в Древнем Египте и Вавилоне. Решались задачи практического характера, таким образом сложились правила арифметических действий. Вавилоняне составили таблицы квадратов, кубов целых чисел, таблицы обратных величин и т.д. . Но наиболее значительные результаты в области изучения чисел были получены в Древней Греции начиная с VI века до нашей эры.

Наивысшего расцвета учения о натуральных числах достигла в школе знаменитого философа и математика Пифагора Самосского (от 580- от 500 до н.э.). Этого необычного учёного при жизни почитали как полубога и чудотворца. Известно, что по политическим мотивам он оставил свой остров Самос и совершил путешествие в Египет и Вавилон, где приобщился к тайнам жрецов. Вернувшись, поселился в Кратоне (греч.Город на юге Италии) и основал тайное общество, которое стала одновременно и политической организацией, и философской научной школы. Традиции школы Пифагора хранились его учениками несколько веков и в этой школе созрело философско-мистическое учение «Пифагореизм».

Пифагорейцы провозгласили основным принципом всего мироздания число и объяснили свойства всех предметов и явлений, исходя из арифметической структуры. Они создали оригинальную арифметику, где каждое число играло свою роль. Натуральными числами обозначались и боги, и космос, и люди, и их взаимоотношения.

Работая над числами, изучая их свойства, учённые не только решали задачи, но и создавали числовые фокусы, которые мы сейчас используем. Например : Загадайте трёхзначное число и припишите к нему его ещё раз. Разделите это число сначала на 7, потом на 11, а потом на 13 (хотя при помощи карандаша).

Несмотря на недоверие, это число разделится и на 7, и на 11, и на 13 и в результате получится задуманное число (это фокус основан на признаке делимости чисел на 7,11,13).

128128 128128/7 18304/11 1664/13

заданное 7 18304 11 1664 13 128

число 58 73 36

56 66 26

21 70 104

21 66 104

28 44 0

28 44

0 0

Россия также не остаётся в стороне от математических преобразований. В 16-17 веках в России начинает появляться и распространяться рукописная математическая литература (этого требует межевание и измерение земель, система податного обложения, градостроительство и важное дело, развивающаяся торговые отношения), многие из этих рукописей перешли в учебники по арифметике и алгебре. Раньше рукописи играли большую роль в распространении математических и практических знаний, они явились той основой, на которой создавались современные учебники математики.

Одним из таких учебников и был учебник Леонида Филипповича Магницкого, в котором систематический курс математики сопровождался историческими задачами и интересными заметками об учёных.

Задачи из учебника Магницкого оказались весьма жизнеспособными, многие из них перешли в последующие учебники, и до нашего времени они часто приводятся авторами арифметических и алгебраических задачников.

Эти задачи весьма интересны, они дают возможность почувствовать колорит и особенности языка той эпохи. Например:

1 Торговец

некий торговец купил 112 баранов старых и молодых, дав 49 рублей 20 алтын, за старого платил по 15 алтын и по 2 деньги, а за молодого по 10 алтын. Сколько старых и молодых баранов он купил?

Примечание: алтын равен 3 копейки

деньга = половине копейки.

Взаимосвязь математики и физики

Ньютон в «Математических началах натуральной философии» говорил о «подчинении явлений законам математики, и, хотя он использовал язык геометрии, для формулировки законов механики ему пришлось создать дифференциальное и интегральное исчисление. Так впервые был осуществлен прорыв за пределы евклидовой геометрии как математической структуры физики. Благодаря усилиям Ньютона, Лейбница, К.Маклорена, Л.Эйлера классическая механика предстала как теория обыкновенных дифференциальных уравнений второго порядка. При этом важнейшую стимулирующую роль в возникновении и развитии математического анализа и теории дифференциальных уравнений сыграли задачи классической механики.

Ньютоновские законы движения благодаря созданию дифференциального и интегрального исчисления отличались от законов и представлений его предшественников тем существенным признаком, что они носили дифференциальный характер. Впервые в науке стало возможным из состояния движения в данный момент времени выводить состояние, непосредственно следующее за ним. Некоторые мыслители считают, что дифференциальный закон является той единственной формой причинного объяснения, которая может полностью удовлетворить современного физика.

В дальнейшем были выявлены и другие математические представления механики, положившие начало феномену аналитической механики, нацеленному на изучение структур классической механики. оказалось, что ее можно сформулировать как вариационное исчисление, как теоерию дифференциальных уравнений с частными производными первого порядка, как риманову геометрию, как симплектическую геометрию. Эти отождествления оказали решающее воздействие на развитие математики в 19 в. и выявили структурно-математическую мощь классической механики. Лагранжев, гамильтонов и другие формализмы аналитической механики обнаружили удивительную живучесть, сыграв важную роль в создании квантовых и релятивистских теорий 20 в. Кстати говоря, аналитическая механика стала первым образцом математической физики, которая, в отличие от теоретической физики, во главу угла ставит исследование математических структур физики.

Классико-механическая программа (и соответствующая картина мира) открыла описанный выше способ математизации точного естествознания, который, несмотря на значительное количество приверженцев, оказался ограниченным. Физика (как наука о свете, теплоте, электричестве и магнетизме), которая, за небольшим исключением, до начала 19 в. не имела теоретического оформления, подобного классической механике, потребовала привлечения нового типа математизации. Решающим поворотом стало интенсивное использование математического анализа для представления феноменологических отношений в теоретической форме, не сводящейся к классической механике. На этом пути в первой четверти 19 в. были созданы (в основном усилиями французских ученых) математическая электростатика, теория теплопроводности, элементы термодинамики, волновая оптика.

В 1860-1870-х гг. создание классической физики, сопряженное с ее математизацией, в основном было завершено (теория электромагнитного поля Максвелла, термодинамика В.Томсона и Р.Клаузиуса, основы статистической механики Максвелла и Л. Больцмана). Математический анализ, и прежде всего теория дифференциальных уравнений в частных производных второго порядка, оставался основной математической структурой классической физики. Но вместе с тем важными дополнительными инструментами ее математизации стали векторное исчисление и теория вероятностей. В кристаллографии получила применение теория групп. К концу 19 в. выявилась фундаментальная особенность основных дифференциальных уравнений классической физики – их вариационная структура, т.е. возможность их получения на основе вариационного исчисления (из вариационных принципов, прежде всего принципа Гамильтона). Забегая вперед, подчеркнем, что и фундаментальные дифференциальные уравнения (поля), фигурирующие в квантовой механике, общей теории относительности, квантовой теории поля и элементарных частиц (т.е. уравнения Шредингера, Эйнштейна, Дирака и др.), как выяснилось впоследствии, тоже выводимы из вариационного принципа. Вариационность основных уравнений физики позволяет связать основные законы сохранения с симметриями (группами инвариантности) соответствующих теорий в духе теоремы Нетер.

Математизация других естественных наук осуществлялась через посредство физики и классической механики (небесная механика, астрофизика, некоторые разделы химии). А.Пуанкаре на рубеже 19-20 вв. связал математико-аналитическую (т.е. опирающуюся на математически анализ и дифференциальные уравнения) природу классической физики с ее локальностью и однородностью. В результате знание элементарного факта позволяло получить описание процесса посредством дифференциальных уравнений, интегрирование которых вело к описанию множества наблюдаемых явлений. Отсутствие в биологии характерных для физики локальности, однородности, простых элементарных соотношений, согласно Пуанкаре, препятствовало математизации биологических наук.

Научная революция, произошедшая в физике в первой трети 20 в., существенно изменила взаимоотношение физики и математики, кроме того, математика сыграла существенную роль в самой этой революции. Прежде всего, при построении теории относительности, особенно общей, и квантовой механики в полной мере проявилась опережающая роль математики, в отличие от классики, в которой математике (дифференциальным уравнениям) предшествовало установление связи физических понятий с математическими величинами, при разработке релятивистских и квантовых теорий отыскание адекватной математической структуры опережало ее физическое осмысление. Так, при создании общей теории относительности сначала была найдена риманова структура пространства-времени и тензорно-геометрическая концепция гравитации и только после этого была прояснена собственно физическая сторона дела. При создании квантовой механики также сначала были установлены математические основы теории (например, уравнение Шредингера для волновой функции, физический смысл которой оставался неясным) и только после этого была развита физическая интерпретация теории (вероятностная трактовка волновой функции, принципы неопределенности и дополнительности). Именно эти достижения теоретической физики позволили говорить о «предустановленной гармонии между математикой и физикой или о «непостижимой эффективности математики в естественных науках». В какой-то степени это выглядело как возрождение пифагорейско-платоновской концепции математизации научного знания или его более современного варианта в духе Кеплера, Ньютона и Лейбница.

Если классическая физика выглядела с математической точки зрения, прежде всего как теория дифференциальных уравнений с частными производными второго порядка и соответственно математико-аналитическая структура была определяющей, то в неклассической физике на передний план выдвинулась теория групп преобразований, дифференциально-геометрические структуры и функциональный анализ. Важное значение сохраняли также теория дифференциальных уравнений и вариационное исчисление, с помощью которого формулировались законы движения, а также теория вероятностей, позволяющая корректно сформулировать понятие состояния в статистической и квантовой механике. Теоретико-инвариантный подход, ставший после создания специальной теории относительности мощным и универсальным средством построения теории, означал распространение «Эрлангенской программы» Ф.Клейна на физику, иначе говоря, вел к пониманию научных теорий прежде всего как теорий инвариантов некоторых лежащих в их основе фундаментальных групп симметрии. Общая теория относительности привела впервые к геометризации физического взаимодействия (именно гравитации) на языке теории римановых искривленных пространств. Переход от классики к квантовой механике соответствовал переходу к бесконечномерному гильбертову пространству состояний и самосопряженным операторам, т.е к переходу от обычного анализа к функциональному анализу. Дальнейшее развитие физики во второй половине 20 в. вводило в оборот такие разделы, как геометрия расслоенных пространств, топология, бесконечно мерные алгебры Ли и т.д.

Триумфы интенсивной математизации в создании неклассической физики привели к такому пониманию роли математики, когда она рассматривается не только как средство количественного описания явлений, но и как генератор фундаментальных физических понятий и теоретических построений. Вплоть до настоящего времени надежды на прорыв в фундаментальной физик теоретики связывают с поиском математических структур, математических образов, ранее не связывавшихся с реальностью. По существу, это близко к методу математической гипотезы, важность которого в неклассической физике подчеркивал еще С.И.Вавилов.

Несмотря на устойчивую традицию считать упомянутую выше «предустановленную гармонию» символом веры теоретиков либо ключевым «эпирическим законом эпистемологии» и поэтому избегать поиска оснований этой гармонии, есть несколько перспективных подходов к ее объяснению (истолкованию).

Первый – историко-научный – опирается на эстафетную модель развития физики (естествознания), согласно которой эта эффективность основана на повторяющейся и сменяющейся игре между мышлением и опытом; на том, что математические концепции в своих истоках восходят к внешнему миру физической реальности, развиваясь затем относительно автономно до мощных абстрактных теорий, которые, в свою очередь, оказываются удивительно подходящими для описания новых пластов естествознания, как бы возвращая ему долг. Существует подход, основанный на резонном замечании об определенном родстве (или даже совпадении) некоторых основных методологических принципов физики и математики. Таковыми, например, являются принципы симметрии (инвариантности), сохранения, соответствия и др. в «предустановленной гармонии» между физикой и математикой, конечно, присутствует эстетический момент. Иногда даже полагают, что целесообразно ввести понятие «математическая красота» физических теорий и что именно с ним связана эта гармония. В процессе математизации происходит своего рода «естественный отбор эффективных структур, и именно с ними ассоциируется понятие «математическая красота». С эти отбором можно связать стремление теоретиков выбирать задачи, имеющие «красивые решения». Само понятие, или чувство, «математической красоты» эволюционировала от закономерностей целых чисел и правильных многогранников к евклидовой геометрии и от нее к математическому анализу и дифференциальным уравнениям, а затем от них к теории групп, дифференциально-геометрическим структурам и функциональному анализу.

Известны также попытки связать «предустановленную гармонию» между физикой и математикой с устройством нашего мозга, с физико-математической природой нашего мышления (сознания). С точки зрения материалистической диалектики последние попытки (независимо от их возможной эвристичности при исследовании некоторых разделов науки) являются совершенно необоснованными.

Связь математики с биологией 
Биология широко использует математический аппарат при проведении тех или иных исследований. Например, ежегодно ученики нашей школы пишут исследовательские работы по биологической и экологической проблематике (например, «Социологическое исследование экологического сознания жителей», «Разработка проекта очистки воды в реке Олым», «Возрастные различия в переключении произвольного внимания у детей и подростков» и др.) Любое исследование предполагает статистическую обработку результатов: ранжирование, построение графиков и диаграмм, подсчёт среднего арифметического, среднеквадратичного отклонения, процентной доли, коэффициентов корреляции. При изучении генетических законов, решении задач по генетике, биохимии и популяционной генетике математический аппарат необходим как при освоении теоретического материала, так и при решении конкретных задач. На протяжении многих лет в школе действует факультатив, рассматривающий золотое сечение в природе. Организация занятий такова, что обучающимся предоставляется широкая возможность самостоятельной работы при подборе материала, подготовке сообщений и презентаций. Хотя занятия на факультативе проводит учитель математики, учителя других профилей не только принимают в них участие, но и на своих уроках используют материал этого курса.

В частности, на уроках биологии мы обращаем внимание на то, что очередное листорасположение подчиняется правилу золотого

сечения: дробь, числитель которой — это число оборотов на стебле, а знаменатель — число листьев в цикле, соответствует рядам Фибоначчи, например, 3/8 или 5/13. Подобную же логарифмическую спираль можно обнаружить в расположении семян в корзинках сложноцветных, чешуй — в шишках голосеменных, колючек на стебле кактусов. Во всех этих случаях спирали заворачиваются навстречу друг другу, а число правых и левых спиралей всегда относится друг к другу как соседние числа в ряду Фибоначчи. Переходя к курсу зоологии, мы вновь

сталкиваемся с логарифмической спиралью в строении раковины моллюска. По законам золотого сечения построены тела бабочек, стрекоз и ящериц, этому же правилу подчиняется форма яиц птиц. Та же логарифмическая спираль обнаруживается и в строении костного лабиринта (улитки) внутреннего уха. Золотую пропорцию можно обнаружить в строении человеческого тела и в чертах лица. Но те только в анатомии можно увидеть золотую пропорцию. Отношение продолжительности систолы и диастолы сердечного цикла также составляет дробь из соседних чисел ряда Фибоначчи. Чем больше сердечный ритм отклоняется от идеальной частоты, тем больше энергетические затраты организма и тем ниже эффективность работы сердца. В курсе общей биологии обязательно отмечается, что двойная спираль молекулы ДНК почти полностью соответствует числам ряда Фибоначчи. Таким образом, на протяжении всего курса биологии учитель имеет возможность с математической точностью обосновать гармоничность природы и единство всех проявлений жизни 

Какова Роль математики в современной науке? 
Роль математики в современной науке постоянно возрастает. Это связано с тем, что, во-первых, без математического описания целого ряда явлений действительности трудно надеяться на их более глубокое понимание и освоение, а, во-вторых, развитие физики, лингвистики, технических и некоторых других наук предполагает широкое использование математического аппарата. Более того, без разработки и использования последнего было бы, например, невозможно ни освоение космоса, ни создание электронно-вычислительных машин, нашедших применение в самых различных областях человеческой деятельности. Благодаря математическим знаниям и навыкам мы решаем не только арифметические задачи. Это наука позволяет развивать гибкость ума, что нужно для принятия объективного решения любой задачи. Эта не только задачи математического характера, но и различные жизненные ситуации, требующие рассмотрения «под разными углами».

Чтобы понять, познать сущность проблемы, нужно рассмотреть ее со всех сторон, что возможно благодаря воображению.математика наука язык Математика - наука точная, которая не терпит ошибок. Именно благодаря этой ее черте математические законы легли в основу всех изобретений, начиная примитивными в виде рычагов и маятников и заканчивая суперкомпьютерами.

Заключение

Математика встречается и используется в повседневной жизни, следовательно, определенные математические навыки нужны каждому человеку. Нам приходится в жизни считать, например, деньги. Мы постоянно используем, часто не замечая этого, знания о величинах, характеризующих протяженности, площади, объемы, промежутки времени, скорости и многое другое. Все это пришло к нам на уроках арифметики и геометрии и сгодилось для ориентации в окружающем мире.

Математические знания и навыки необходимы практически во всех профессиях, прежде всего, конечно, в тех, что связаны с естественными науками, техникой и экономикой. Но несомненна необходимость применения математических знаний и математического мышления врачу, лингвисту, историку, и трудно оборвать этот список, настолько важно математическое образование для профессиональной деятельности в наше время. Следовательно, математика и математическое образование нужны для подготовки к будущей профессии. Для этого необходимы знания из алгебры, математического анализа, теории вероятности и статистики.

Философское постижение мира, его общих закономерностей и основных научных концепций также не возможно без математики. И потому математика необходима для формирования мировоззрения.

Математика должна способствовать освоению этических принципов человеческого общежития. Изучение ее призвано воспитывать в человеке интеллектуальную честность, объективность, стремление к постижению истины, она воспитывает также способность к эстетическому восприятию мира, красоты интеллектуальных достижений.

«Математику уже затем учить надо, что она ум в порядок приводит», - М.В. Ломоносов. Не только руки, ноги, тело требуют тренировки, но и мозг человека требует упражнений. Решение задач, головоломок, математических ребусов развивает логическое мышление, скорость реакции. Недаром говорят, что математика – это гимнастика ума.

Однако, как кажется мне, математическая наука абсолютно лишает мир многообразия. Как выразился русский математик И.Шафаревич она «убивает индивидуальность». Он пишет: «Мы имеем, скажем, яблоко, цветок, кошку, дом, солдата, студента, луну. Можно сосчитать и объявить, что их 7. Но 7 чего? Единственный ответ: "7 предметов". Различия между солдатом, луной, яблоком и т.д. исчезают. Они все потеряли свою индивидуальность и превратились в лишенные признаков "предметы"». То есть счёт делает предметы равными.

Невозможно, конечно, отрицать, что современный мир нельзя представить без математики и её достижений, но лично я предпочитаю углубляться в другие школьные предметы.

Диаграмма

я провела опрос среди учащихся 9 классов на тему : «В каком предмете математика важнее всего?» И вот, что у меня получилось

Русский -10%

Физика-25%

Литература-10%

Алгебра-40%

Геометрия-15%

Список используемой литературы

1. https://multiurok.ru/files/issliedovatiel-skii-proiekt-23.html

2. http://megapredmet.ru/1-44329.html

3. https://ru.wikipedia.org/wiki/

4. Лиман М.М. Школьникам о математике и математиках: пособие для учащихся 4-8 классов / М.М. Лиман. – М.: Просвещение, 1981. – 180с.

5. . Энциклопедический словарь юного математика / Под ред. Б.В. Гнеденко. г.Москва, 1989г. - 313с.