Проект по математике на тему _ как научиться быстро считать_

Тема проекта:

Как научиться быстро считать

Автор проекта: Грабарев Иван, обучающийся 7 класса

МБОУ «Нижнесанарская СОШ».

Наставник проекта:Баймышева Ольга Марковна,

учитель математики.

2019

Оглавление

1. Аннотация наставника

2. Введение ………………………………………………………………………………3

3. 1. Теоретическая часть………………………………………………………… 4

1.1 Предпосылки быстрого счета…………………................................................4

1.1.1 Изменение счета при появлении цивилизации……………………………….4

1.2 Различные приемы быстрого счета…………...………………………………….5

1.3 Практическое применение быстрого счета...………………………………….. 9

1. . Практическая часть………………………………………………………… 11

2.1. Выступление в 7 классе по теме проекта ……………..……………………… .11

1. Заключение ………………………………………….………………………………..13

2. Список использованных источников………………………………………………..14

3. Приложение…………………………………………………………………………...15

Введение

В наш век высоких технологий и повсеместного использования компьютера умение быстро и правильно считать в уме не утратило своей актуальности. Такие навыки помогут человеку в учёбе, в быту, в профессиональной деятельности. Кроме того, быстрый счёт – настоящая гимнастика для ума, приучающая в самых сложных жизненных ситуациях находить в кратчайшее время хорошие и нестандартные решения.

Я выбрал тему «Как научиться быстро считать» потому, что я хотел бы научиться считать быстро и правильно, не прибегая к использованию калькулятора.

Проблемные вопросы моей работы следующие:

• Может ли человек считать быстро?

• Какие приёмы вычислений существуют?

• Где пригодятся приёмы вычислений в жизни?

Актуальность темы заключается в том, что быстрый счёт помогает людям в повседневной жизни, а ученикам на «отлично» заниматься по математике.

Цель работы: пропаганда приёмов быстрого счета

Задачи:

• выяснить применяют ли школьники приемы быстрого счета;

• изучение источников, в которых встречаются различные приемы быстрого счета;  

• составить памятку для учащихся для применения приемов быстрого счета;

• выступить перед учащимися 7 класса с целью ознакомления с различными приёмами быстрого счёта.

Объект исследования − приёмы быстрого счёта.

Предмет исследования − процесс вычислений.

Гипотеза исследования: если показать, что применение приемов быстрого счета, облегчает вычисления, то можно добиться того, что повысится вычислительная культура учащихся, и  им будет легче решать практические задачи.

При выполнении работы  были использованы следующие приемы и методы: опрос (анкетирование),  анализ (статистическая обработка данных), работа с источниками информации, практическая работа, наблюдения.

Ход исследования:

• Постановка целей;

• Сбор материала (интернет, дополнительная литература);

• Анализ собранного материала;

• Сообщение «Как научиться быстро считать» для учеников 7 класса

1. Теоретическая часть.

1.1. Предпосылки быстрого счета

Никто не знает, как впервые появилось число, как первобытный человек начал считать. Однако десятки тысяч лет назад первобытный человек собирал плоды деревьев, ходил на охоту, ловил рыбу, научился делать каменный топор и нож, и ему приходилось считать различные предметы, с которыми он встречался в повседневной жизни. Постепенно возникала необходимость отвечать на жизненно важные вопросы: по сколько плодов достанется каждому, чтобы хватило всем, сколько расходовать сегодня, чтобы оставить про запас, сколько нужно сделать ножей и т.п. Таким образом, сам не замечая, человек начал считать и вычислять.

Вначале человек научился выделять единичные предметы. Например, из стаи волков, стада оленей он выделял одного вожака, из выводка птенцов – одного птенца и т.д. Научившись выделять один предмет из множества других, говорили «один», а если их было больше – «много».

Частые наблюдения множеств, состоящих из пары предметов (глаза, уши, крылья, руки) привели человека к представлению о числе два. До сих пор слово «два» на некоторых языках звучит так же, как «глаза» или «крылья».

Если предметов было больше двух, то первобытный человек говорил «много». Лишь постепенно человек научился считать до трёх, затем до пяти и до десяти и т.д. Название каждого числа отдельным словом было великим шагом вперёд.

Для счёта люди использовали пальцы рук, ног. Ведь и маленькие дети тоже учатся считать по пальцам. Однако этот способ годился только в пределах двадцати.

Выход нашелся: считать на пальцах до 10, а затем начинать сначала, отдельно подсчитывая количество десятков. Система счисления на основе десяти возникла как естественное развитие пальцевого счёта.

1.1.1. Изменение счёта при появлении цивилизации.

По мере развития речи люди начали использовать слова для обозначения чисел. Отпала необходимость показывать кому-то пальцы, камешки или реальные предметы, чтобы назвать их количество. Для изображения чисел стали применяться рисунки, чертежи или символы. Существовали и системы с отдельными символами для каждой цифры до 9 включительно, как в арабской системе счисления, которую мы сейчас используем, а у греков имелся специальный символ и для 10.

При помощи пальцев рук люди научились не только считать большие числа, но и выполнять действия сложения и вычитания.

Древние торговцы для удобства счёта начали накладывать зерна и раковины на специальную дощечку, которая со временем стала называться абаком.

Особенно сложны и трудны были в старину действия умножения и деления, особенно последнее. «Умноженье – мое мученье, а с деленьем – беда» – говорили в старину. Тогда не существовало еще, как теперь, одного выработанного практикой приёма для каждого действия.

1.2 Различные приемы быстрого счета.

1. Умножение на 11

Закономерность здесь такая:

53 х 11 = 583
Шаг 1 — Складываем две цифры двузначного числа: 5 + 3 = 8
Шаг 2 — Помещаем результат между двумя числами двузначного числа: 583

59 х 11 = 649
Шаг 1 — 5 + 9 = 14
Шаг 2 — Перекидываем единицу налево, если сумма на предыдущем шаге оказалась больше 9: 5 + 1 = 6 (справа остается второй символ, в данном случае это четверка)
Шаг 3 — На первый символ мы единицу уже перекинули, получили 6. Далее у нас осталась 4, которую ставим в центр, и дописываем 9: 649

2. Быстрое возведение в квадрат

Этот прием поможет быстро возвести в квадрат двузначное число, которое заканчивается на 5.

85 х 85 = 7225
Шаг 1 — Умножаем первую цифру на первую цифру, увеличенную на единицу: 8 x (8 + 1) = 72
Шаг 2 — Дописываем к получившемуся результату 25: 7225

45 x 45 = 2025
Шаг 1 — 4 х (4 + 1) = 20
Шаг 2 — 2025

3. Умножение на 5

Возьмите любое число, разделите на 2 (другими словами, поделите пополам). Если в результате получилось целое число, припишите 0 в конце. Если нет, не обращайте внимание на запятую и в конце добавьте 5.

Это срабатывает всегда:
2682×5 = (2682 / 2) & 5 или 0
2682 / 2 = 1341 (целое число, поэтому добавьте 0)
13410
Давайте попробуем другой пример:
5887×5
2943,5 (дробное число, пропустите запятую, добавьте 5)
29435

4. Умножение на 9

Это просто. Чтобы умножить любое число от 1 до 9 на 9, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например, 9×3 – загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9×3 – это 2), затем посчитайте после загнутого пальца (в нашем случае – 7).

Ответ – 27.

5.Умножение на 4 и на 8

Чтобы устно умножить число на 4, его дважды удваивают. Например:

112*4 =224*2=448

335*4 = 670*2 =1340

Чтобы устно умножить число на 8, его трижды удваивают. Например:

217*8 = 434*4=868*2=1736

(Eще удобнее: 217*8=200*8 +17*8= 1600*13=1736.

6. Деление на 4 и на 8

Чтобы устно разделить число на 4, его дважды делят пополам. Например:

76:4 =38:2=19

236:4=118:2=59

Чтобы устно разделить число на 8, его трижды делят пополам. Например:

464:8=232:4=116:2=58

516:8=258:4=129:2= 64 ½

7.Умножение на 1¹/₂, на 1 ^1/₄, на 2¹/₂, на ³/₄

Чтобы устно умножить число на 1¹/₂ прибавляют к множимому его половину. Например:

34*1¹/₂ = 34 + 17=51

23*1¹/₂=23 + 11¹/₂ = 34¹/₂ (или 34,5)

Чтобы устно умножить число на 1¹/₄ прибавляют к множимому его четверть. Например:

48*1¹/₄ =48 +12=60

58*1¹/₄ = 58+14 ¹/₂=72¹/₂ или 72,5

Чтобы устно умножить число на 2¹/₂. к удвоенному числу прибавляют половину множимого.

Например: 18*2¹/₂.=36+9= 45;

39*2¹/₂.= 78 + 19'¹/₂.= 97¹/₂ (или 97,5)

Другой способ состоит в умножении на 5 и делении пополам:

18*2¹/₂ = 90:2 = 45

Чтобы устно умножить число на ³/₄ (т. е. чтобы найти ³/₄ этого числа), умножают число на 1¹_/2 и делит пополам. Например:

30 * ³/₄ = (30+15)/2= 22¹/₂ (или 22,5)

8. Деление на 5

На самом деле делить большие числа на 5 очень просто. Все, что нужно,— просто умножить на 2 и перенести запятую: 195 / 5
Шаг1: 195×2 = 390
Шаг2: Переносим запятую: 39,0 или просто 39.
2978 / 5
Шаг1: 2978×2 = 5956
Шаг2: 595,6

9. Перемножение двузначных чисел, меньших, чем 20.

К одному из чисел надо прибавить количество единиц другого, эту сумму умножить на 10 и прибавить к ней произведение единиц данных чисел:

18•16=(18+6) • 10+8•6= 240+48=288.  

 Описанным способом можно умножать двузначные числа, меньшие 20, а также числа, в которых одинаковое количество десятков: 23•24 = (23+4) • 20+4•6=27•20+12=540+12=562.

Объяснение:

(10+a) • (10+b) = 100 + 10a + 10b + a•b = 10• (10+a+b) + a•b = 10• ((10+a)+b) + a•b .

10. Умножение двузначного числа на 101.

Пожалуй, самое простое правило: припишите ваше число к самому себе. Умножение закончено. 
Пример: 57 • 101 = 5757 57 -- 5757

Объяснение: (10a+b) •101 = 1010a + 101b = 1000a + 100b + 10a + b 
Аналогично производят умножение трехзначных чисел на 1001, четырехзначных - на 10001 и т.п.

11. Умножение на 22, 33, …, 99.

Чтобы двузначное число умножить 22,33, …,99, надо этот множитель представить в виде произведения однозначного числа на 11. Выполнить умножение сначала на однозначное число, а потом на 11:

15 •33= 15•3•11=45•11=495.

12.Китайско-японский метод умножения.

В Японии ученики первого класса могут перемножать трёхзначные числа, не зная таблицу умножения. Для этого используется простейший метод с рисованием полосок. Логика метода понятна из рисунка.

После рисования нужно всего лишь посчитать количество пересечений в каждой области .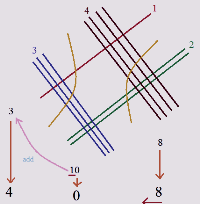

Таким методом можно п еремножать даже трёхзначные числа.

13.Русский крестьянский способ умножения

В России несколько веков назад среди крестьян некоторых губерний был распространен способ, который не требовал знание всей таблицы умножения. Надо было лишь уметь умножать и делить на 2. Этот способ получил название КРЕСТЬЯНСКИЙ (существует мнение, что он берет начало от египетского).

Пример: умножим 47 на 35

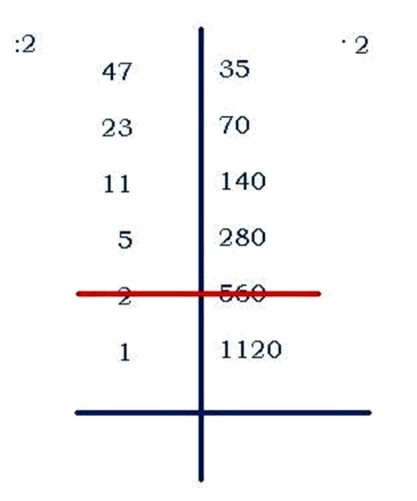
• запишем числа на одной строчке, проведём между ними вертикальную черту;

• левое число будем делить на 2, правое – умножать на 2 (если при делении возникает остаток, то остаток отбрасываем);

• деление заканчивается, когда слева появится единица;

• вычёркиваем те строчки, в которых стоят слева чётные числа;

• далее оставшиеся справа числа складываем – это результат.

14. Метод решетки Аль-Хорезми

У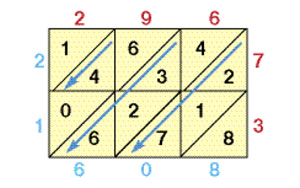 множение чисел методом решётки имеет следующий алгоритм:
1. Записать множители таким образом, чтобы было соответствие между цифрами первого множителя и столбцами решётки — слева направо, а также между цифрами второго множителя и строками решётки — сверху вниз.
2. Перемножить цифры первого и второго множителей в парах, при этом записав все результаты в местах пересечения строки и столбца, причём десятки должны находиться в левой верхней половине клетки, а единицы - в правой нижней половине.
3.  Начиная с правой стороны, найти сумму чисел из соседних диагоналей решётки, причём единицы суммы нужно отмечать в своей диагонали, прибавляя к сумме из соседней левой диагонали число, которое было образовано старшими разрядами.
4. Получившееся число и есть искомое произведение.

1.3 Практическое применение быстрого счета

        В своём исследовании я решил провести анкетирование учащихся 5,7 классов, чтобы выяснить, знают ли ученики приёмы быстрого счёта. Если да, то применяют ли на уроках математики эти умения, а если не знают, то выяснить - хотели бы узнать.

        При обработке данных, я выяснил следующее:

1. Зачем нужно уметь считать?

а) пригодится в жизни, например, считать деньги;(37%)

б) чтобы хорошо учиться в школе; (20%)

в) чтобы быстро решать; (29%)

г) чтобы быть математически грамотным; (10%)

д) не обязательно уметь считать. (4%)

2. Знаешь ли ты приемы быстрого счета?

а) да, несколько (9%);

б) нет, не знаю (91%).

3. Применяешь ли ты при вычислениях приемы быстрого счета?

а) да; (3%)

б) нет (97%)

4. Хотели бы вы узнать приемы быстрого счета, чтобы быстро считать?

а) да; (83%)

б) нет (17%).

Также я встретился с выпускниками нашей школы, которые сдают ЕГЭ и ОГЭ и спросил их: «Что, по их мнению, нужно для успешной сдачи экзамена?» Они сказали, что нужно знать все математические формулы, уметь применять их и правильно и быстро считать.

Анализ результатов: проанализировав результаты, я сделал вывод, что большинство учеников считает, что умение считать пригодится в жизни и необходимо в школе, особенно при изучении математики, физики, химии, информатики. Приемы быстрого счета знают несколько учеников и почти все хотели бы научиться быстро, считать.

Поэтому я решил выступить перед своими одноклассниками и познакомить их с теми приемами быстрого счета, которые я сам изучил.

2.Практическая часть.

2.1. Выступление в 7 классе по теме проекта.

Ход мероприятия:

1. Анализ анкетирования;

2. Какие приемы вычислений существуют;

3. Использование приёмов быстрого счёта (повторная самостоятельная работа).

4. Заключение.

1. Анализ результатов.

Я проанализировал результаты и пришел к выводу, что 37 % считают, что умение быстрого счёта пригодится в жизни; а что помогает хорошо учиться, быстро решать разные задачи, быть математически грамотным – 59%; и что необязательно уметь считать – 4 %.Приёмы быстрого счета знают не так уж много учащихся (9%), а не знают и хотели бы знать – 91%.

После этого я решил провести эксперимент, цель которого узнать, помогут ли приёмы быстрого счёта улучшить вычислительные навыки учащихся.

В начале я предложил ребятам различные примеры (20) и попросил решить их за 10 минут, но многие ребята с этим не справились.

2. Какие приёмы вычислений существуют.

Потом я провел с ребятами занятие, где показал приёмы быстрого счёта:

1. Умножение на 11;

2. Быстрое возведение в квадрат двузначного числа, оканчивающегося на 5;

3. Деление на 5;

4. Умножение двузначного числа на 101;

5. Русско-крестьянский способ умножения;

6. Метод решетки (Аль-Хорезми);

7. Китайско – японский метод умножения.

3. Использование приёмов быстрого счёта (повторная самостоятельная работа)

После этого занятия мы еще раз провели самостоятельную работу с похожими примерами, результаты работы стали намного лучше.

4. Заключение.

Я думаю, что результаты самостоятельной работы улучшились, благодаря тому, что ребята использовали приёмы быстрого счёта.

Мои одноклассники очень заинтересовались этой темой, поэтому я решил сделать для них памятку по применению приёмов быстрого счёта (Приложения).

ЗАКЛЮЧЕНИЕ

Существуют способы быстрого сложения, вычитания, умножения, деления, возведения в степень. Я рассмотрел лишь немногие способы быстрого счета. Все рассмотренные мною методы устного вычисления говорят о многолетнем интересе ученых и простых людей к игре с цифрами. Используя некоторые из этих методов на уроках или дома, можно развить скорость вычислений, добиться успехов в изучении всех школьных предметов. Умножение без калькулятора – тренировка памяти и математического мышления. Мне было интересно работать над проектом, я выступил перед учащимися 7 класса, раздал памятки. Надеюсь, что ребята воспользуются данными приёмами и будут успешно применять их в своей работе.

Список используемой литературы

1. Виленкин Н.Я. За страницами учебника математики: Пособие для учащихся 5-6 кл. сред. шк. – М.: Просвещение, 1989. – 287 с.: ил.

2. Перельман Я.И. Живая математика. - Екатеринбург, Тезис, 1994.

3. Перельман Я.И. Быстрый счет. - Екатеринбург, Тезис, 1994.

4. Борода Л.Я., Борисов А.М. Некоторые формы по привитию интереса к математике. //Математика в школе. -  1990, №11.– с.39-44.

Приложение № 1

АНКЕТА

1. Зачем нужно уметь считать?

    а) пригодится в жизни, например, считать деньги;

    б) чтобы хорошо учиться в школе;    в) чтобы быстро решать;        

    г) чтобы быть грамотным;                  д) не обязательно уметь считать.

2. Знаешь ли ты приемы быстрого счета?

    а) да, много;       б) да, несколько;      в) нет, не знаю.

3. Применяешь ли ты при вычислениях приемы быстрого счета?

      а) да;       б) нет.

4. Хотели бы вы узнать приемы быстрого счета, чтобы быстро считать?

      а) да;       б) нет.

Приложение № 2

Памятка «ПРИЁМЫ БЫСТРОГО СЧЁТА»

1) Умножение на 11 числа, сумма цифр которого не превышает 10. Чтобы умножить на 11 число, сумма цифр которого 10 или меньше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить 1, а вторую и последнюю (третью) цифру оставить без изменения.

72 * 11=7(7+2)2=792

2) Умножение на 11 числа, сумма цифр которого больше 10. Чтобы умножить на 11 число, сумма цифр которого 10 или больше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить 1, а вторую и последнюю (третью) цифру оставить без изменения.

78 * 11=7(7+8)8=7(15)8=858

3) Умножение двузначного числа на 101. Самое простое правило: припишите ваше число к самому себе.

57 * 101 = 5757

4) Умножение трёхзначного числа на 999. Любопытная особенность числа 999 проявляется при умножении на него всякого другого трёхзначного числа. Тогда получается шестизначное произведение: первые три цифры есть умножаемое число, только на уменьшенное на единицу, а остальные три цифры (кроме последней) – «дополнения» первых до 9.

385 * 999 = 384615

5) Умножение на 5

Возьмите любое число, разделите на 2 (другими словами, поделите пополам). Если в результате получилось целое число, припишите 0 в конце. Если нет, не обращайте внимание на запятую и в конце добавьте 5.

Это срабатывает всегда:
2682×5 = (2682 / 2) или 5, или 0
2682 / 2 = 1341 (целое число, поэтому добавьте 0)
13410
Давайте попробуем другой пример:
5887×5
2943,5 (дробное число, пропустите запятую, добавьте 5)
29435

6) Китайско-японский метод умножения.

7) Русский крестьянский способ умножения

• запишем числа на одной строчке, проведём между ними вертикальную черту;

• левое число будем делить на 2, правое – умножать на 2 (если при делении возникает остаток, то остаток отбрасываем);

• деление заканчивается, когда слева появится единица;

• вычёркиваем те строчки, в которых стоят слева чётные числа;

далее оставшиеся справа числа складываем – это результат.

8) Метод решетки Аль-Хорезми

1 . Записать множители таким образом, чтобы было соответствие между цифрами первого множителя и столбцами решётки — слева направо, а также между цифрами второго множителя и строками решётки — сверху вниз.
2. Перемножить цифры первого и второго множителей в парах, при этом записав все результаты в местах пересечения строки и столбца, причём десятки должны находиться в левой верхней половине клетки, а единицы - в правой нижней половине.
3.  Начиная с правой стороны, найти сумму чисел из соседних диагоналей решётки, причём единицы суммы нужно отмечать в своей диагонали, прибавляя к сумме из соседней левой диагонали число, которое было образовано старшими разрядами.
4. Получившееся число и есть искомое произведение.

Приложение № 3

1. Умножение на 11.

58*11 32*11

23*11 49*11

81*11 92*11

2. Возведение в квадрат двузначных чисел, заканчивающихся на 5.

55² 35²

75² 65²

15² 95²

3. Умножение на 5.

1682*5 4576*5

5687*5 8637*5

3219*5 5633*5

4. Умножение на 101.

37*101 87*101

64*101 46*101

17*101 29*101

5. Русско-крестьянский способ.

56*38 49*35

63*26 57*63

49*15 86*17

6. Метод решетки Аль-Хорезми.

215*73 612*26

56*17 63*12

317*65 516*23

7. Китайско – японский метод.

32*12 56*13

18*26 15*57

Приложение №4 Фотографии

23