Проект по теме "Теорема Пифагора" 8 класс

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №4

ГРУППОВОЙ ИТОГОВЫЙ ПРОЕКТ

НА ТЕМУ

«Теорема Пифагора»

Выполнили:

Прошина Наталия

Резник Виктория

Савченко Леонид

Литвинова Арина

ученики: 8 в класса

МБОУ СОШ №4

Руководитель проекта:

Зубенко Наталья Федоровна

учитель математики

г. Светлоград, 2021 год

Содержание

      Введение……………………………………………………………….……..3    

1. Биография Пифагора……………………………………………….……..4

2. История теоремы Пифагора……………………………………….……..7

3. Различные способы доказательства теоремы Пифагора…………….....10

1. Древнекитайское доказательство………………………………....10

2. Доказательство Гарфилда………………………………………....11

3. Простейшее доказательство……………………………………....11

4. Доказательство Бхаскары……………………………………...….12

5. Доказательство древних индусов………………………………...12

6. Доказательство с использованием свойства подобия…………..13

7. Доказательство Перигаля……………………………………..…..13

1. Применение теоремы Пифагора……………………………………..….14

Заключение……………………………………………….………………….23

Список источников……………………………………….…………………25

\

Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора, а другое деление отрезка в среднем и крайнем отношении. Первое можно сравнить с мерой золота, второе же больше напоминает драгоценный камень»

Иоганн Кеплер

Введение

     На уроке геометрии мы познакомились с одной из важнейших теорем геометрии для прямоугольного треугольника, известной с древних времен – теоремой Пифагора. Кратко познакомились с историей этой теоремы, рассмотрели ее доказательство, но также узнали, что это одно из ее доказательств. Трудно найти человека, для которого имя Пифагора не ассоциировалось бы с его теоремой. Пожалуй, у каждого взрослого, жизнь которого совершенно не связана с математикой, со школьной скамьи осталось в памяти, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Причина такой популярности теоремы Пифагора очевидна: простота, красота и широкая значимость.

     В самом деле, теорема Пифагора проста, но не очевидна. Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Но, кроме того, теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.), свидетельствует о гигантском числе ее конкретных реализаций. Зная теорему Пифагора можно находить ее новые применения и способы доказательств. Теорема Пифагора занесена в Книгу рекордов Гиннеса, как теорема с наибольшим количеством доказательств.

    Нас заинтересовали эти факты, поэтому решили продолжить знакомство с историей теоремы, ее доказательствами и практической значимостью в деятельности человека. В этом актуальность своей работы.

     Цель работы: выяснить различные способы доказательства теоремы Пифагора и изучить ее применение при решении задач.

     Задачи:

1. Изучить историю открытия теоремы Пифагора;

2. Познакомиться с различными способами доказательства теоремы

   Пифагора;

1. Подобрать примеры старинных задач, которые решаются с помощью теоремы Пифагора.

Основная часть

1. Биография Пифагора

     Историю жизни Пифагора трудно отделить от легенд, представляющих его в качестве совершенного мудреца и великого учёного, посвящённого во все таинства греков и варваров. Ещё Геродот называл его «величайшим эллинским мудрецом». Мы не можем знать достоверно историю Пифагора, поскольку  самые ранние известные источники об учении Пифагора появились лишь 200 лет спустя после его смерти. Сам Пифагор не оставил сочинений, и все сведения о нём и его учении основываются на трудах его последователей, не всегда беспристрастных.

     Пифагор родился в Сидоне Финикийском примерно в 570 до н. э. С ранних лет он обнаружил необыкновенную одарённость. Родителями Пифагора были Мнесарх и Партенида с острова Самос. По одной из версий Мнесарх был камнерезом, по другой – он был богатым купцом из Тира, получившим самосское гражданство за раздачу хлеба в неурожайный год. Мать Пифагора Партенида происходила из знатного рода Анкея, основателя греческой колонии на Самосе.

     Рождение ребёнка будто бы предсказала Пифия в Дельфах, потому Пифагор и получил своё имя, которое значит «тот, о ком объявила Пифия». В частности, Пифия сообщила Мнесарху, что Пифагор принесёт столько пользы и добра людям, сколько не приносил и не принесёт в будущем никто другой.

          Античный философ Ямвлих пишет, что Пифагор в 18-летнем возрасте покинул родной остров и, объехав мудрецов в разных краях света, добрался до Египта, где пробыл 22 года, пока его не увёл в Вавилон в числе пленников персидский царь Камбис. Нахождение в плену принесло пользу, ему было чему поучиться. Ведь в те годы математика в Вавилоне была более развитой чем в Египте. Наиболее поразительными были успехи алгебры. Вавилоняне изобрели и применяли при счёте позиционную систему счисления, умели решать линейные, квадратные и некоторые виды кубических уравнений. Двенадцать лет он провел за изучением математики, геометрии и магии. И, возможно, именно вавилонская геометрия причастна к доказательству соотношения сторон треугольника и истории открытия теоремы. У Пифагора было для этого достаточно полученных знаний и времени. Но, что это произошло в Вавилоне, документального подтверждения или опровержения тому нет.

     Итак, спустя двенадцать лет, Пифагор, наконец, смог вернуться на Самос в 56-летнем возрасте, где соотечественники признали его мудрым человеком.

     Ямвлих сообщает: «Его философия распространилась, вся Эллада стала восхищаться им, и лучшие и мудрейшие мужи приезжали к нему на Самос, желая слушать его учение. Сограждане, однако, принуждали его участвовать во всех посольствах и общественных делах. Пифагор чувствовал, как тяжело, подчиняясь законам отечества, одновременно заниматься философией, и видел, что все прежние философы прожили жизнь на чужбине. Он уехал в Италию, считая своим отечеством страну, где больше способных к обучению людей».

     Так Пифагор поселился в греческой колонии Кротоне в Южной Италии,  где нашёл много последователей.   

 Пифагор умело использовал знания, полученные в странствиях по свету. Со временем ученый прекращает выступления в храмах и на улицах. Уже в своем доме Пифагор учил медицине, принципам политической деятельности, астрономии, математике, музыке, этике и многому другому. Из его школы вышли выдающиеся политические и государственные деятели, историки, математики и астрономы. Это был не только учитель, но и исследователь. Исследователями становились и его ученики. Пифагор развил теорию музыки и акустики, создав знаменитую «пифагорейскую гамму» и проведя основополагающие эксперименты по изучению музыкальных тонов: найденные соотношения он выразил на языке математики. В Школе Пифагора впервые высказана догадка о шарообразности Земли. Мысль о том, что движение небесных тел подчиняется определенным математическим соотношениям, идеи «гармонии мира» и «музыки сфер», впоследствии приведшие к революции в астрономии, впервые появились именно в Школе Пифагора. Пифагору традиция приписывает введение слов философия и философ.

     Многое сделал ученый и в геометрии. Ему приписывают открытие и доказательство теоремы Пифагора, создание таблицы Пифагора. В школе Пифагора геометрия впервые оформляется в самостоятельную научную дисциплину. Именно Пифагор и его ученики первыми стали изучать геометрию систематически - как теоретическое учение о свойствах абстрактных геометрических фигур, а не как сборник прикладных рецептов по землемерию.
     Важнейшей научной заслугой Пифагора считается систематическое введение доказательства в математику, и, прежде всего, в геометрию. Строго говоря, только с этого момента математика и начинает существовать как наука, а не как собрание древнеегипетских и древневавилонских практических рецептов. С рождением же математики зарождается и наука вообще, ибо «ни одно человеческое исследование не может называться истинной наукой, если оно не прошло через математические доказательства» (Леонардо да Винчи).

     Ученики Пифагора образовали своего рода религиозный орден, или братство посвящённых, состоящий из касты отобранных единомышленников, буквально обожествляющих своего учителя — основателя ордена.

      В основе вещей лежит число, учил Пифагор, познать мир — значит познать управляющие им числа. Изучая числа, пифагорейцы разработали числовые отношения и нашли их во всех областях человеческой деятельности. Числа и пропорции изучались с тем, чтобы познать и описать душу человека, а познав, управлять процессом переселения душ с конечной целью отправить душу в некое высшее божественное состояние.

     Пифагор утверждал, чтобы понять Бога, человек должен познать такие науки как алгебра и геометрия, знать астрономию и понимать музыку. Исследовательская работа сводилась к познанию мистической стороны чисел и философии. Следует отметить, что проповедованные в то время Пифагором принципы, имеют смысл и находят подтверждение и в настоящее время.

     В современном мире Пифагор считается великим математиком и космологом древности, однако ранние свидетельства до III в. до н. э. не упоминают о таких его заслугах.  Таким образом, жизнь Пифагора для нас остается неизведанной доподлинно загадкой, его учение полно мистики, но не лишено смысла и актуальности даже в наши дни.

     Источники сообщают, что Пифагор прожил 80 или 90 лет. Из этого следует дата смерти 490 до н. э. или 480 до н. э.

1. История теоремы Пифагора

     Для нас имя Пифагора связано прежде всего с теоремой Пифагора.                     В настоящее время известно, что эта теорема не была открыта Пифагором. Однако одни полагают, что именно Пифагор первым дал ее полноценное доказательство, а другие отказывают ему и в этой заслуге. Связанная с именем Пифагора, теорема была известна задолго до рождения великого философа. Так в Египте еще пять тысячелетий назад при строительстве сооружений учитывалось соотношение сторон прямоугольного треугольника. А в вавилонских текстах упоминается о все том же соотношении сторон прямоугольного треугольника за 1200 лет до рождения Пифагора.

     Возникает вопрос, почему же тогда история гласит, что возникновение этой теоремы   связано с Пифагором? Ответ может быть только один - он доказал соотношение сторон в треугольнике. Он сделал то, что века назад не делали те, кто просто пользовался соотношением сторон и гипотенузы, установленным опытным путем. 

     Исторический обзор теоремы Пифагора начнем с древнего Китая. Здесь особое внимание привлекает математическая книга Чу-пей. В этом сочинении так говорится о прямоугольном треугольнике со сторонами 3, 4 и 5:

«Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3,    

а высота 4».

    Очень легко можно воспроизвести их способ построения. Возьмем веревку длиною в 12 м с узлами на каждом метре и вобьем колышки в землю, прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра.

     Несколько больше было известно о теореме Пифагора вавилонянам.             Геометрия у индусов была тесно связана с культом. В сочинениях, относящихся к 4 или 5 веку до н.э., мы встречаемся с построением прямого угла при помощи треугольника со сторонами 15, 36, 39.

     В средние века теорема Пифагора определяла границу, если не наибольших возможных, то, по крайней мере, хороших математических знаний. Характерный чертеж теоремы Пифагора, который ныне иногда превращается школьниками, например, в облаченного в мантию профессора или человека в цилиндре, в те времена нередко употреблялся как символ математики. 

     Приведем различные формулировки теоремы Пифагора в переводе с греческого, латинского и немецкого языков.

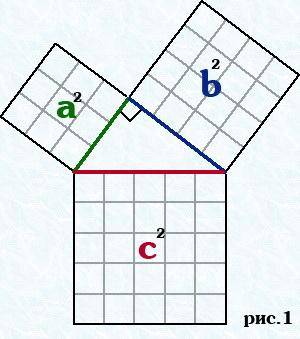
     У Евклида эта теорема гласит (дословный перевод):

     В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

     Латинский перевод арабского текста:

     «Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол».

     Перевод с немецкого (около 1400 года):

     «Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу».

     В первом русском переводе евклидовых «Начал», теорема Пифагора изложена так:

     «В прямоугольном треугольнике квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол».

      Как видим, в разных странах и разных языках существуют различные варианты формулировки знакомой нам теоремы

1. Различные способы доказательства         теоремы Пифагора.

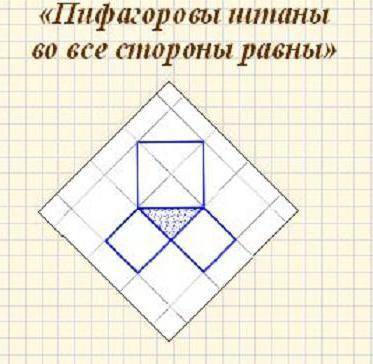
     В наше время известно множество доказательств теоремы Пифагора.     3.1. Древнекитайское доказательство.

     На древнекитайском чертеже четыре равных прямоугольных треугольника с катетами a, b и гипотенузой с уложены так, что их внешний контур образует квадрат со стороной a+b, а внутренний – квадрат со стороной с, построенный на гипотенузе.

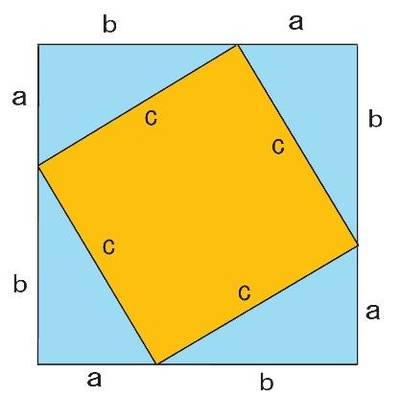
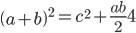
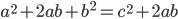
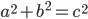
     3.5. Доказательство древних индусов.

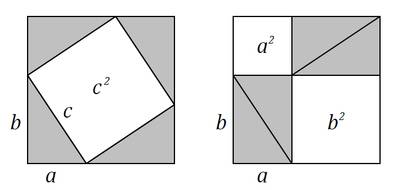
     Здесь изображено два равных квадрата. Длина сторон каждого квадрата равна (a+b). Каждый из квадратов разбит на части, состоящие из квадратов и прямоугольных треугольников. Ясно, что если от площади всего квадрата отнять четыре площади прямоугольных треугольников с катетами a и b, то останутся равные площади, то есть 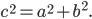  Теорема доказана.

 3.2. Доказательство Джеймса Абрахама Гарфилда (20-й президент США с марта по сентябрь 1881 года ).

     На рисунке три прямоугольных треугольника составляют трапецию. Поэтому площадь данной фигуры можно находить либо по формуле площади прямоугольной трапеции, либо как сумму площадей трех треугольников.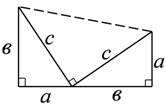 

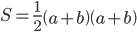
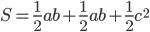
    Приравнивая эти выражения, получим

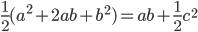
     Раскрывая скобки и сокращая, получим

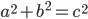
     Теорема доказана.

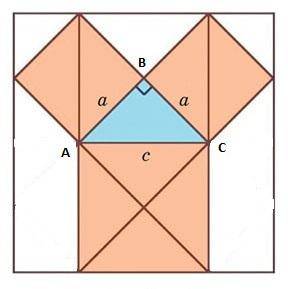
     3.3. Простейшее доказательство.

Простейшее доказательство получается в случае равнобедренного прямоугольного треугольника. Для треугольника АВС: квадрат, построенный на гипотенузе АС, содержит четыре исходных треугольника, а квадраты, построенные на катетах, - по два. Теорема доказана.

     3.4. Доказательство Бхаскары.

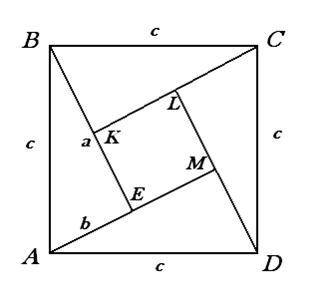
     Пусть АВСD квадрат, сторона которого равна гипотенузе прямоугольного треугольника АВЕ (АВ = с, ВЕ = а, ЕА = b).

     Пусть СК ┴ BE, DL ┴ CK, AM ┴ DL, BE ┴ AM 

ΔABE = ΔBCK = ΔCDL = ΔDAM,

значит KL = LM = ME = EK = a-b.

Площадь квадрата, построенного на гипотенузе AB прямоугольного треугольника ABE,  равна сумме площадей четырех прямоугольных треугольников и квадрата, длина стороны которого равна  (a-b).

Тогда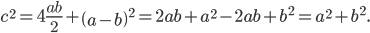 

     Значит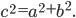 

Теорема доказана.

      3.6. Доказательство с использованием свойства подобия.

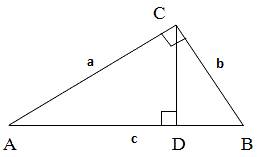
В прямоугольном треугольнике ACB проведем высоту CD. Поскольку треугольники ACB, ADC и CDB подобные, то

,

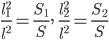где l, l₁, l₂ – соответственные линейные элементы этих треугольников, а S, S₁, S₂ – их площади. Сложив эти два равенства, получим

a² + b² = c². Теорема доказана.

     3.7. Доказательство Перегаля.

   Через центр квадрата, построенного на большем катете, проводят вертикальную и горизонтальную линии (перпендикулярную и параллельную гипотенузе соответственно). В результате получаются соответственно равные многоугольники, которые  одинаково пронумерованы.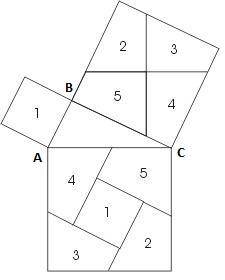

1. Теорема Пифагора при решении задач (старинные задачи)  

Заключение.

     В заключение приведу основные выводы по работе.

     Теорема Пифагора – одна из основополагающих теорем геометрии. Она применяется для решения огромного количества геометрических задач. Является примером простоты, красоты и широкой значимости.

Теорема названа его именем, потому что Пифагор доказал соотношение сторон в треугольнике. Он сделал то, что века назад не делали те, кто просто пользовался соотношением сторон и гипотенузы, установленным опытным путем.

     Со временем доказательств теоремы Пифагора все прибавлялось. На сегодняшний день их насчитывается более пятисот. Теорема даже занесена в Книгу рекордов Гиннеса, как имеющая наибольшее число доказательств.

     В работе приведены несколько способов доказательства теоремы Пифагора, не изучаемых в школе.

Общий вывод работы:

• Теорема Пифагора – одна из важнейших теорем геометрии;

• На ее основании решается множество задач геометрии;

Список литерат

1. Акимова С. Занимательная математика, серия "Нескучный учебник". – Санкт-Петербург. : "Тригон", 1997.

2. Волошников А.В. Пифагор: союз истины, добра и красоты. – М.: Просвещение, 1993.

3. Еленьский Ш. По следам Пифагора. М., 1961.

4. Литцман В. Теорема Пифагора. М., 1960.

5. По следам теоремы Пифагора. М: Самообразование, 2000.

6. Рассчитываем длину стропил и свесов двухскатной крыши // kryshagid.ru/stropilnaya-sistema/kak-rasschitat-dlinu-stropil-dvuxskatnoj-kryshi.html

7. //ru.wikipedia.org

8. //www.youtube.com/watch?v=TqCVqSHBTus

Приложение

Занимательные и исторические задачи по теме «Теорема Пифагора»

1.Для крепления мачты нужно установить 4 троса. Один конец каждого троса должен крепиться на высоте 12 м, другой на земле на расстоянии 5 м от мачты. Хватит ли 50 м троса для крепления мачты?

2.У египтян была известна задача о лотосе:

"На глубине 12 футов растет лотос с 13-футовым стеблем. Определите, на какое расстояние цветок может отклониться от вертикали, проходящей через точку крепления стебля ко дну". Попробуйте сами решить эту задачу. Естественно, при решении использовалась теорема Пифагора.

3.Исторические задачи очень часто представляли в стихах

Задача Бхаскари

«На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»

Задача древних древних индусов :

Над озером тихим,

С полфута размером, высился лотоса цвет.

Он рос одиноко. И ветер порывом

Отнес его в сторону. Нет

Боле цветка над водой.

Нашел же рыбак его ранней весной

В двух футах от места, где рос.

Итак, предложу я вопрос:

Как озера вода здесь глубока.

CD – глубина озера, обозначим ее x. Тогда по теореме Пифагора имеем: BD² – x²= BC², то есть (x + 0,5)² – x²= 2², x² + x + 0,25 – x²= 4, x= 3,75. Ответ: глубина озера равна 3,75 фута.

4.Задача о бамбуке из древнекитайского трактата "Гоу-гу"

Имеется бамбук высотой в 1 чжан. Вершину его согнули так, что она касается земли на расстоянии 3 чи от корня (1 чжан = 10 чи).Какова высота бамбука после сгибания?

5.Задача из учебника «Арифметика» Леонтия Магницкого

«Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать».

13