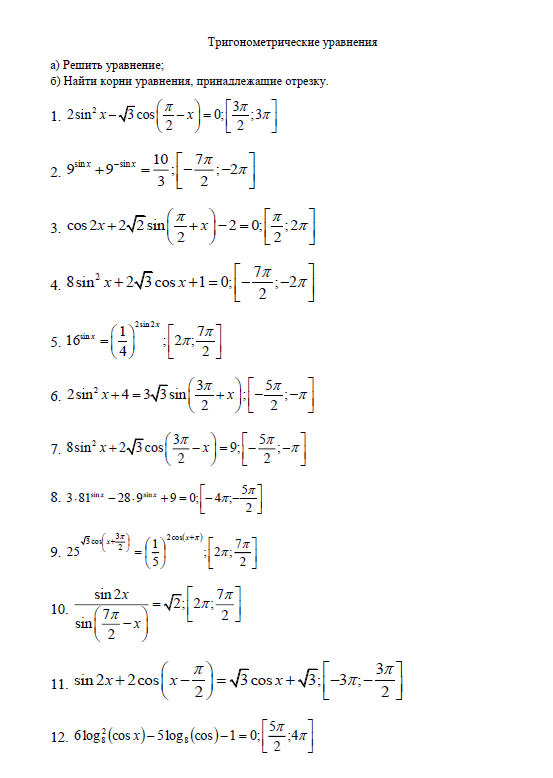0
Федеральное государственное казённое общеобразовательное учреждение
«Омский кадетский военный корпус
Министерства обороны Российской Федерации»

Проектная (исследовательская) работа
Тригонометрические уравнения:
виды и способы решения.
Автор: обучающийся 11-3 класса
Дускин Владислав
Руководитель:
преподаватель математики
Железная Н.О.
г. Омск
2022 год
Оглавление
Введение 3
1. Тригонометрические уравнения: виды, способы решения. 5
1. 1. Решение простейших тригонометрических уранений 5
1. 2. Основные способы решения тригонометрических уранений 6
1. 3. История понятия «тригонометрия» 15
2. Практикум «Решение тригонометрических уравнений» 18
2.1. Самостоятельные работы № 1, № 2 18
2.2. Обучающий тренажер и итоговый тест по теме
«Решение тригонометрических уравнений» 22
Заключение 27
Список литературы и использованных сайтов 28
ПРИЛОЖЕНИЕ 31
Введение
Кто с детских лет занимается математикой,
тот развивает внимание, тренирует свой мозг,
свою волю, воспитывает настойчивость
и упорство в достижении цели.
А. Маркушевич
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение данной темы в 4 четверти 10 класса. Сейчас я учусь в 11 классе и 1 июня 2023 года мне предстоит сдавать ЕГЭ по математике профильного уровня. Как часто тригонометрические уравнения встречаются на ЕГЭ? Тригонометрические уравнения могут встретиться до четырех раз в заданиях ЕГЭ. Это может быть:
Задача № 5 (простейшее тригонометрическое уравнение – встречается время от времени);
Задача № 8 (задача с прикладным содержанием, которая включает в себя решение тригонометрического уравнения – встречается изредка);
Задача № 11 (она на производную, но в конечном счёте сводится к решению простейшего тригонометрического уравнения – ЧАСТО ВСТРЕЧАЕТСЯ В ЕГЭ)
Задача № 12 – даёт 2 первичных балла – (решение тригонометрического уравнения средней или высокой сложности – ОЧЕНЬ ЧАСТО, ПРАКТИЧЕСКИ ВСЕГДА!)
Так что навык решения данного вида уравнений может добавить в мою копилку целых 5 первичных баллов из 31! Это наиболее актуально для меня сейчас, потому что каждый первичный балл важен, чем он больше - тем лучше для поступления.
В вариантах ЕГЭ задача 12, где нужно решить уравнение, состоит из двух пунктов. Первый пункт – решение самого уравнения. Второй – нахождение его корней на некотором отрезке. Некоторые из методов (например, замена переменной или разложение на множители) являются универсальными, то есть применяются и в других разделах математики. Другие являются специфическими именно для тригонометрии. Решение тригонометрических уравнений в большинстве случаев проводится либо с помощью замены переменной, либо разложения на множители, но и тот, и другой способ применяется в разных вариантах в зависимости от вида конкретного уравнения. Поэтому в данном проекте предлагается рассмотреть и изучить более подробно классификацию типов тригонометрических уравнений и методов их решения.
Были определены:
Объектная область исследования - учебный предмет «математика».
Объект исследования – решение тригонометрических уравнений.
Предмет исследования – математические задачи определённого типа.
Цель проекта:
- Повторение, обобщение и систематизация имеющихся знаний по теме «Тригонометрические уравнения»;
- Расширение и углубление знаний по теме «Решение тригонометрические уравнения», выработка навыка решения различных типов тригонометрических уравнений;
- Формирование устойчивого интереса к математике, умения и навыков исследовательской, проектной деятельности; развитие навыков самостоятельного поиска информации, формирование умения отбирать и структурировать материал.
Задачи:
Изучить литературу по теме проекта;
Систематизировать все собранные материалы;
Подготовить подборку задач по теме проекта и представить полученные результаты в виде обучающего тренажера;
Тип проекта:
по виду деятельности – практико-ориентированный;
по организационной форме – индивидуальный;
по времени выполнения - долговременный.
Этапы работы над проектом
Разработанный нами проект включает два этапа:
1-й этап аналитический
2-й этап обобщения
Основные виды работы над проектом:
Изучение дополнительной литературы (справочники, словари, энциклопедии, задачники по математике, Интернет-ресурсы)
- Анализ полученной информации (обобщение, сравнение, сопоставление с имеющимися знаниями по данной теме, решение задач).
Глава 1. Тригонометрические уравнения: виды, способы решения
Определение. Тригонометрическое уравнение — алгебраическое уравнение относительно тригонометрической функции неизвестного аргумента.
1.1. Простейшие тригонометрические уравнения
Частные случаи:
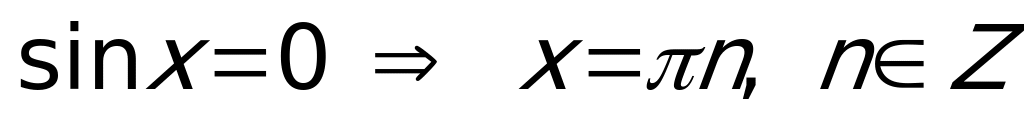 ,
,
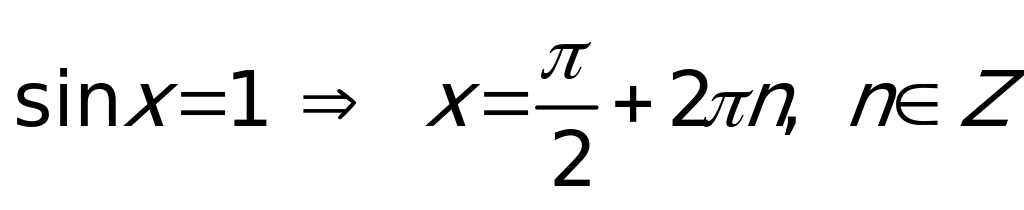 ,
,
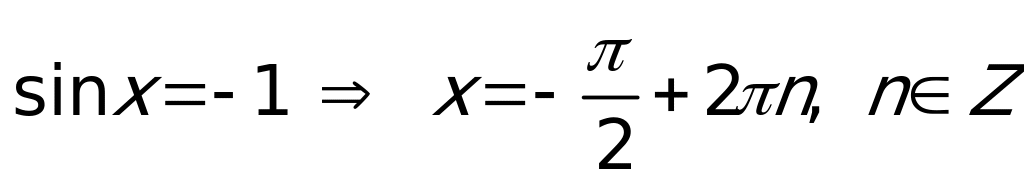 ,
,
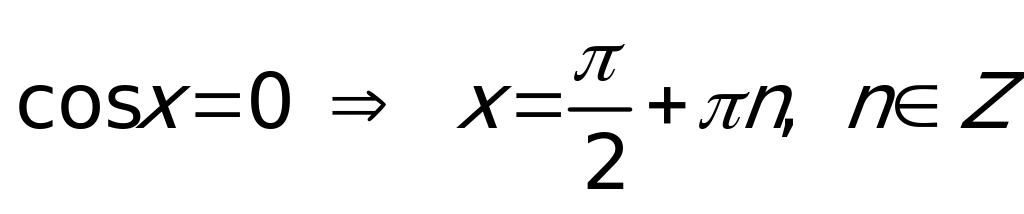 ,
,
 ,
,
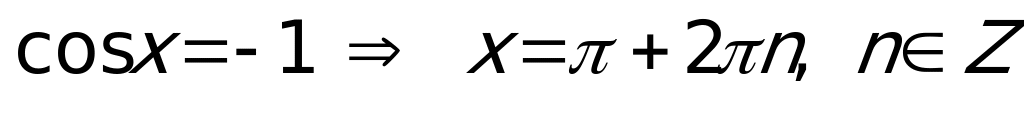 ,
,
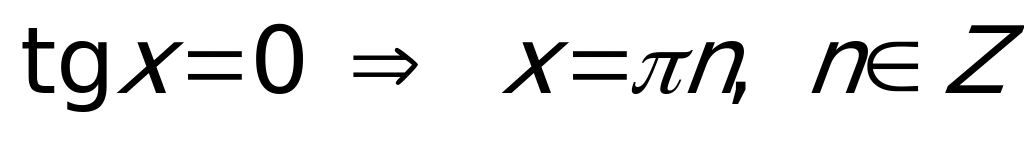 ,
,
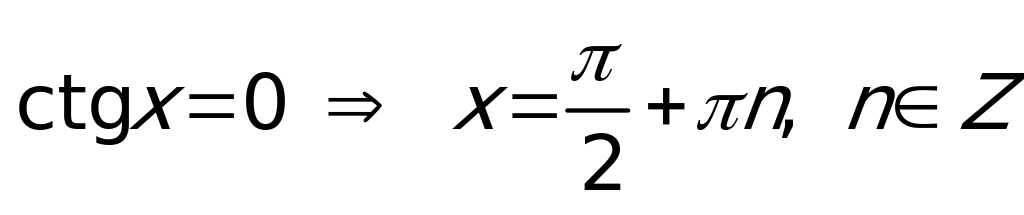 ;
;
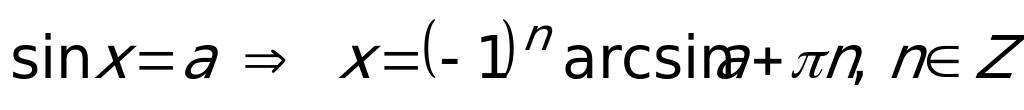 ;
;
 ;
;
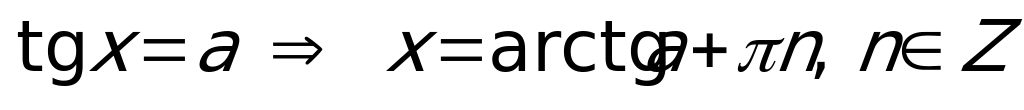 ;
;
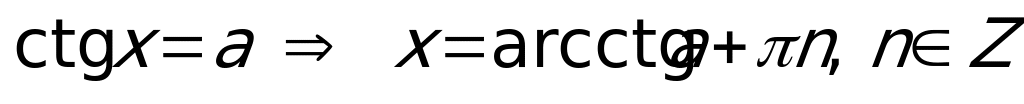 .
.
Пример 1. Решите уравнения
1) 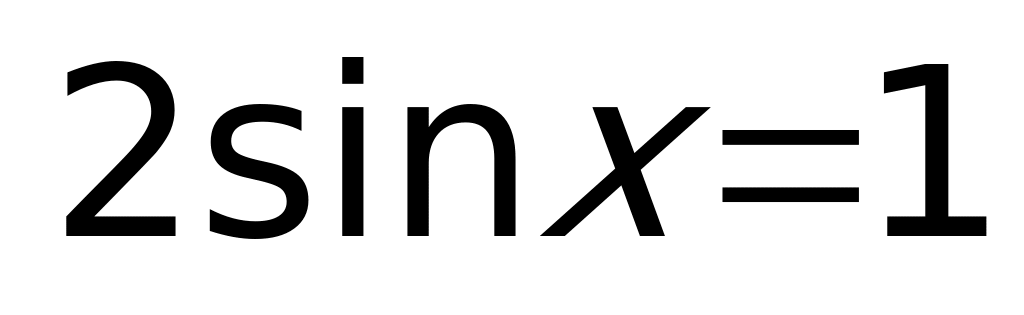 ;
;
2) 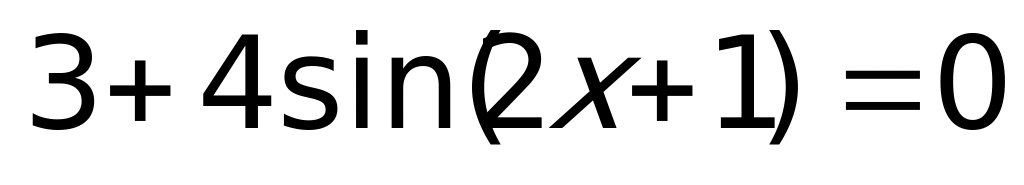 ;
;
3) 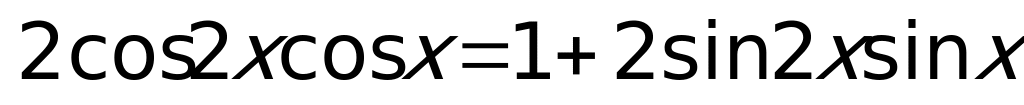
4) 
1.2. Основные способы решений тригонометрических уравнений
Основные способы:
разложение на множители;
введение новых переменных.
Пример 2. 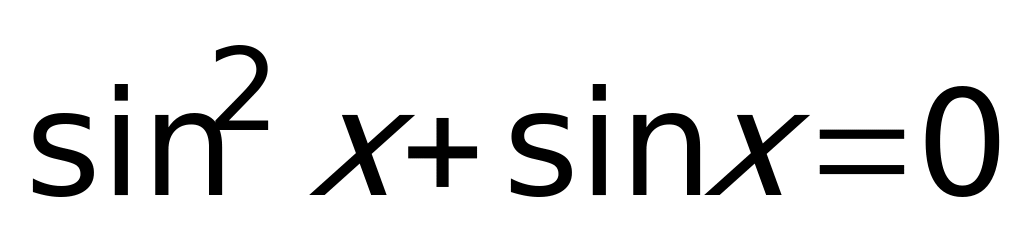 Ответ:
Ответ: 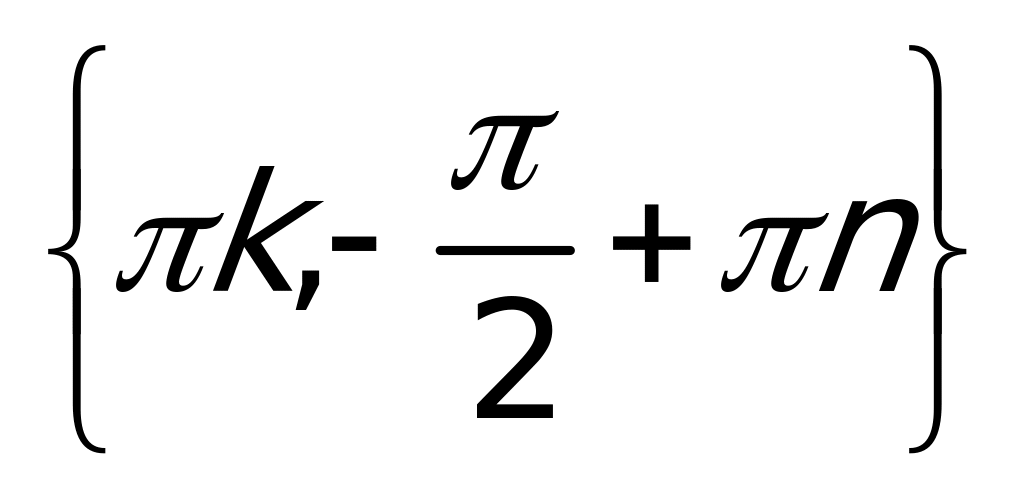
Пример 3. 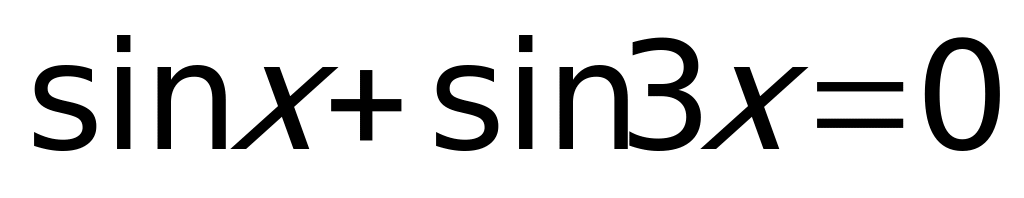
Решение: 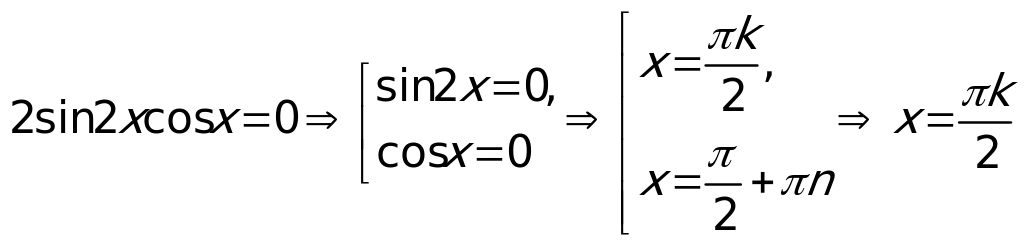 Ответ:
Ответ: 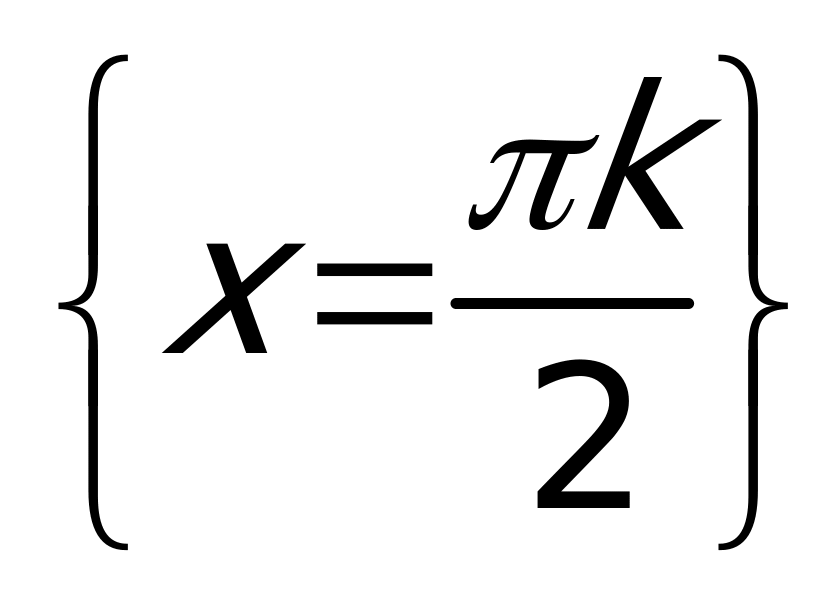
Пример 4. 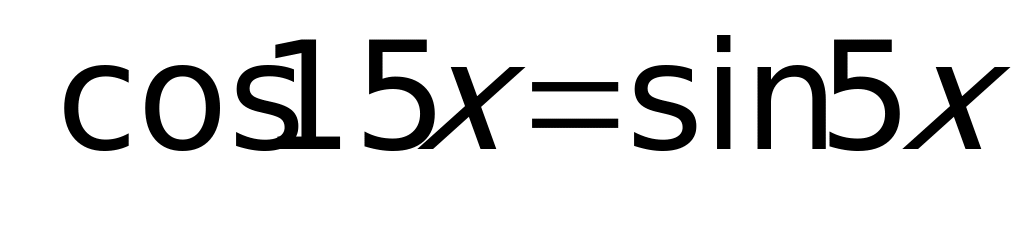 .
.
Решение: ОДЗ: 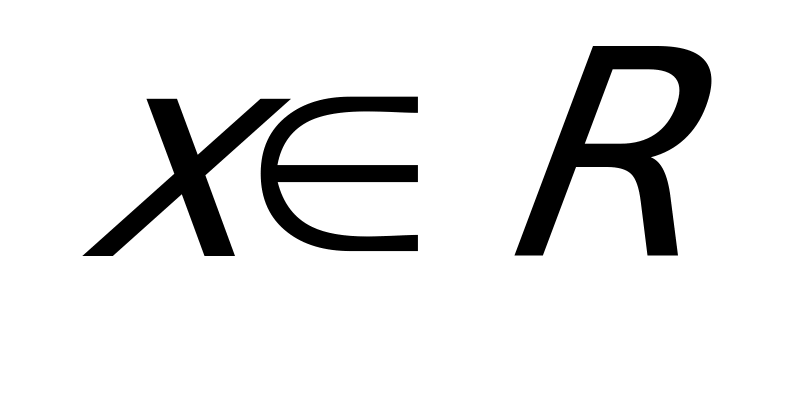 . Так как
. Так как 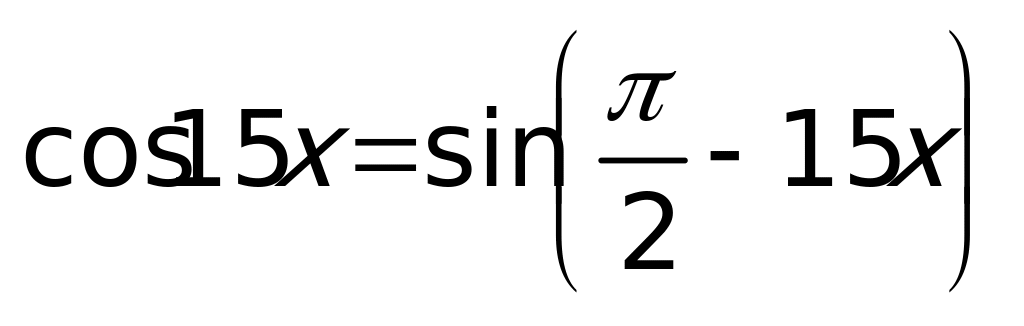 , получим:
, получим: 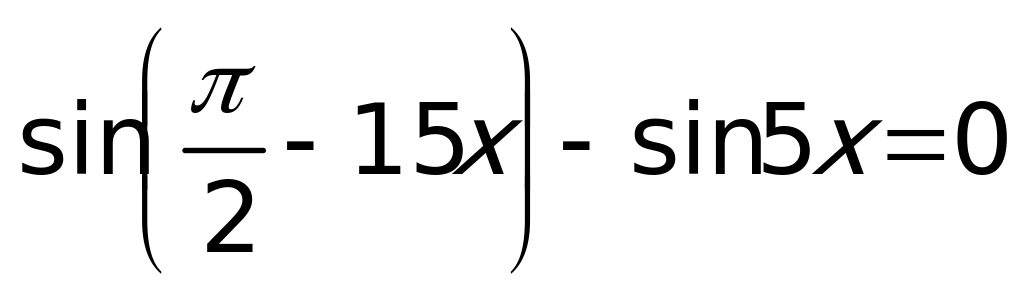 или
или 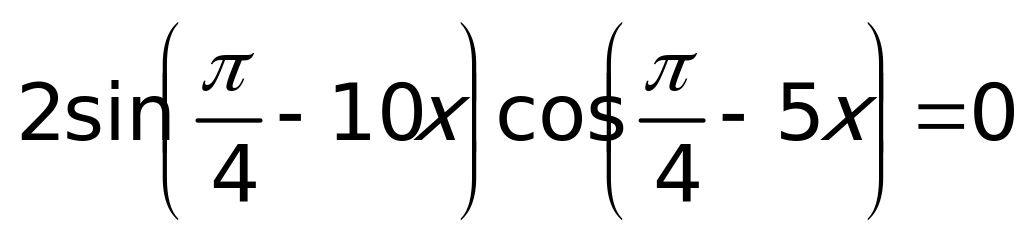 , откуда
, откуда
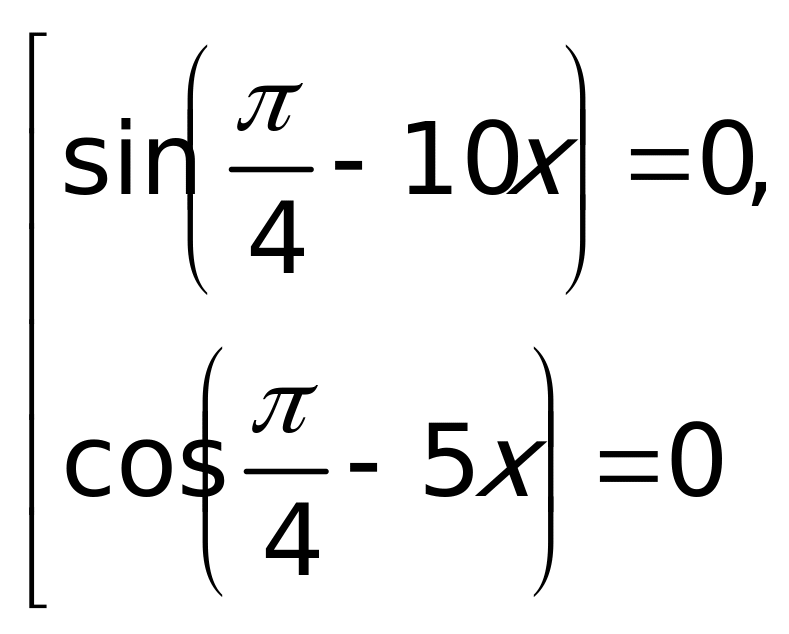
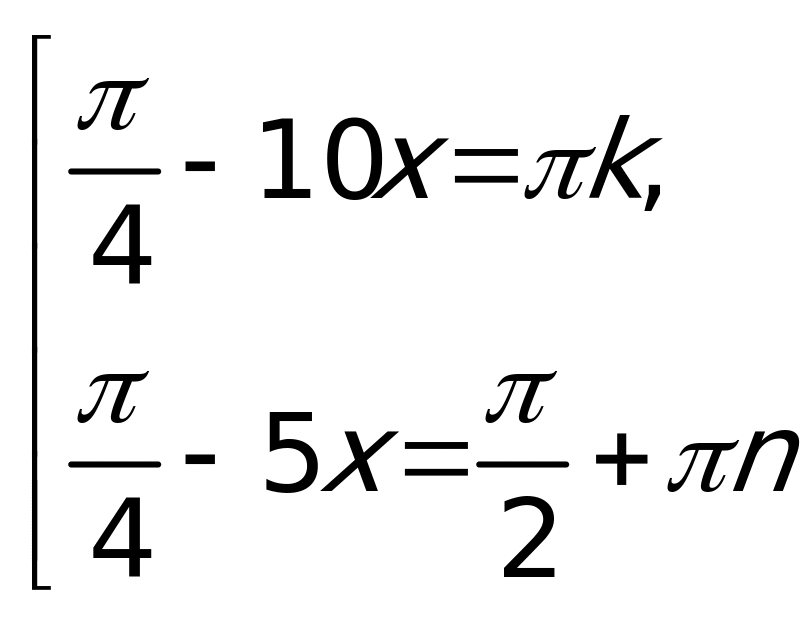
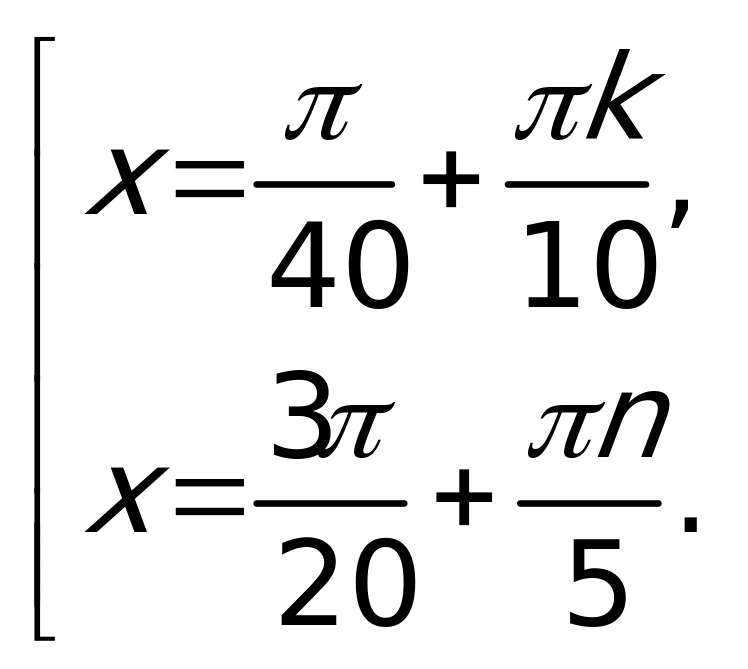
Ответ: 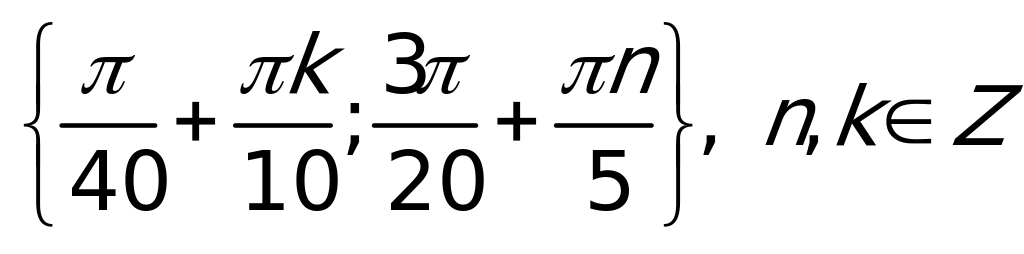 .
.
Общая схема решения тригонометрических уравнений:
Указать ОДЗ уравнения.
С помощью тригонометрических формул и различных преобразований свести исходное уравнение к одному или нескольким простейшим.
Решить каждое из полученных простейших уравнений и записать ответ, объединяя полученные решения.
Проверить, входят ли найденные решения в ОДЗ.
Проверка найденных решений необходима, если в процессе решения:
произошло расширение области определения уравнения в результате некоторых преобразований (освобождение от знаменателей, сокращение дроби, приведение подобных членов);
использовалось возведение обеих частей уравнения в одну и ту же четную степень;
применялись тригонометрические тождества, левая и правая части которых имеют неодинаковые области определения (например: 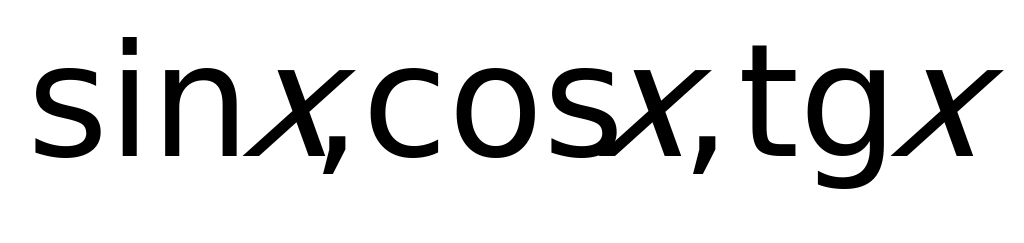 через
через 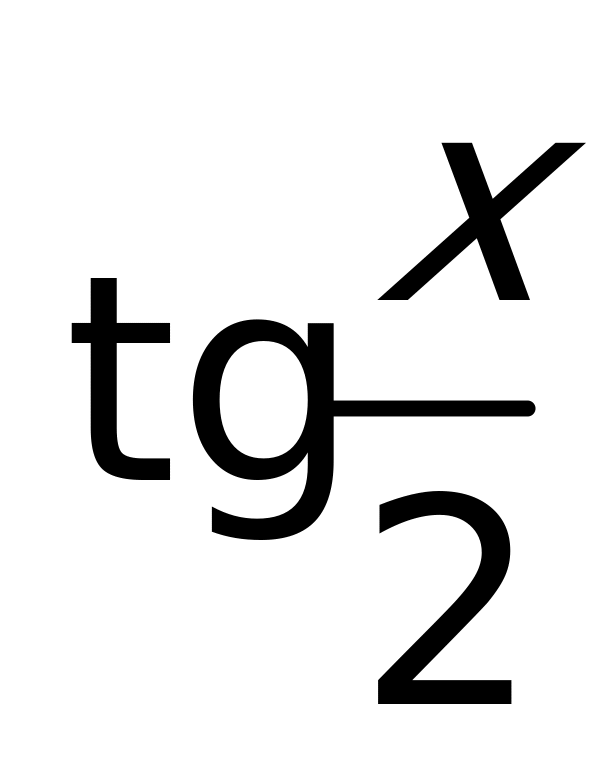 ,
, 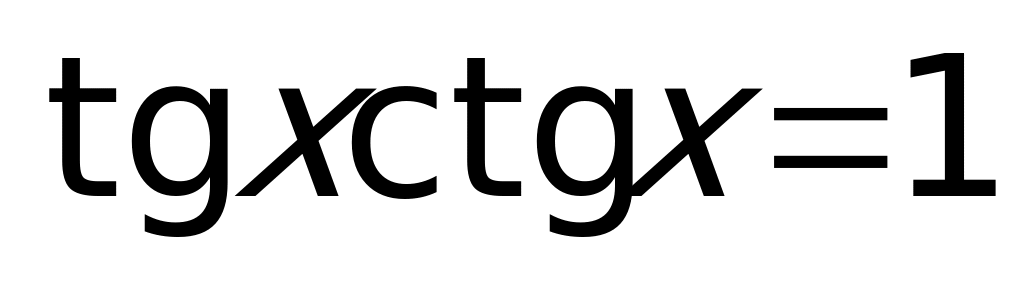 ,
, 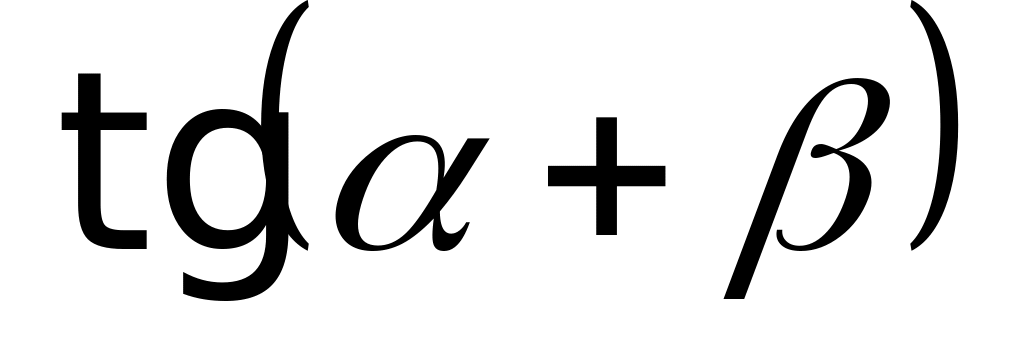 и др.).
и др.).
Чтобы не потерять корни в результате тождества преобразования, надо проверить все запрещаемые этим преобразованием значения переменной.
Пример 5. 
Решение: ОДЗ: 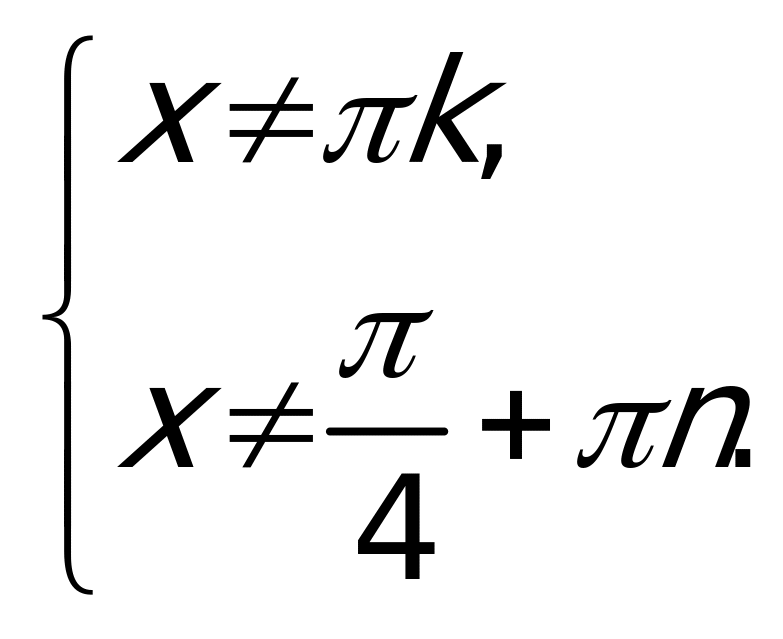 Пусть
Пусть 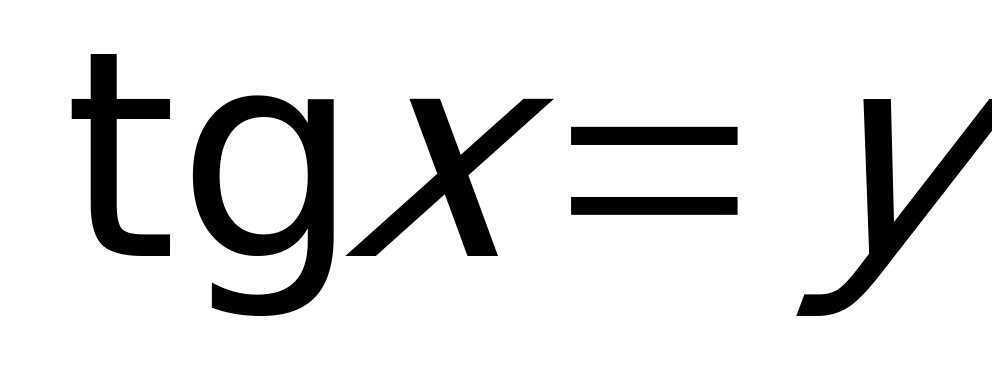 , тогда
, тогда 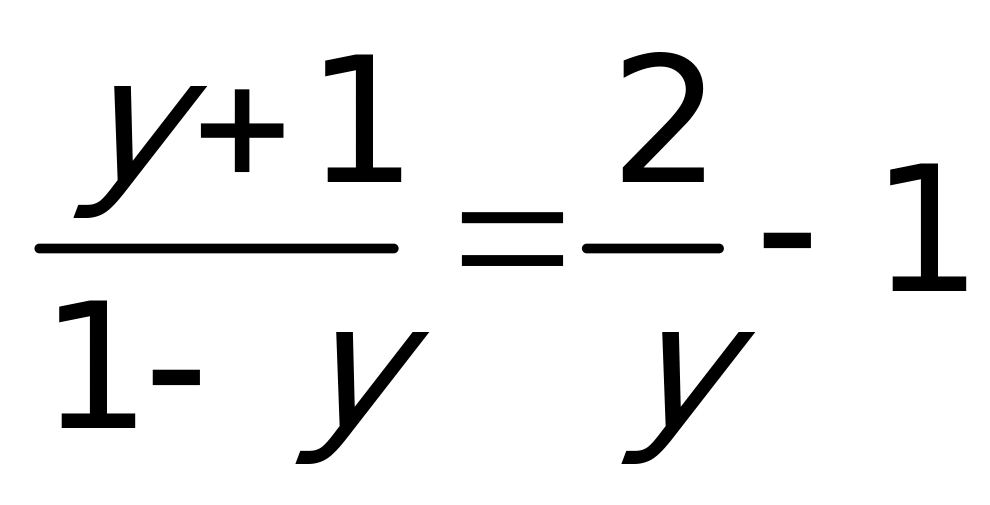 . Получим
. Получим 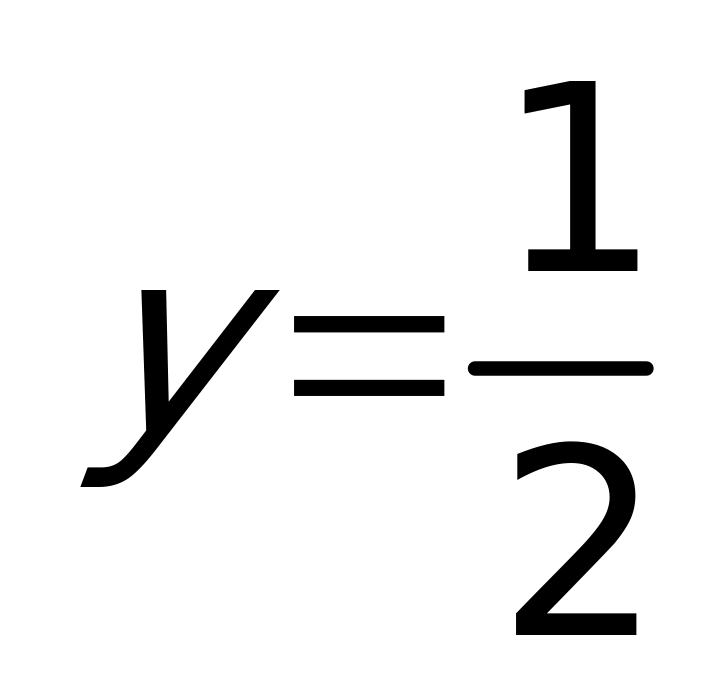 или
или 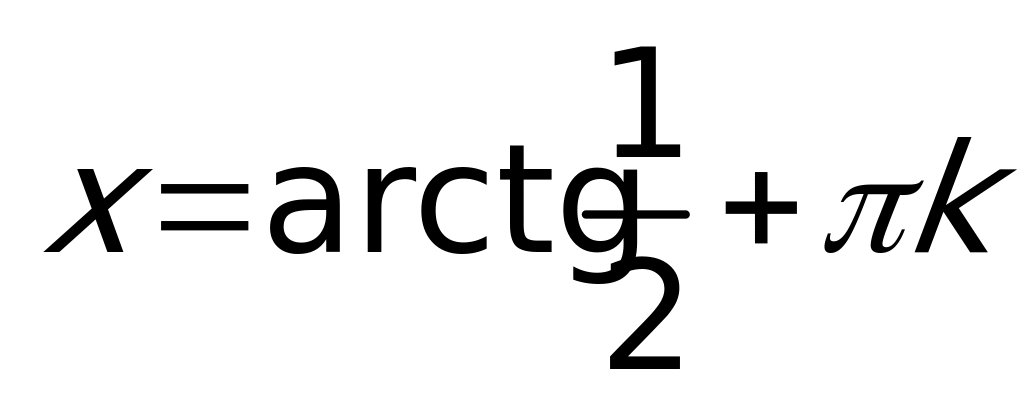 , но
, но 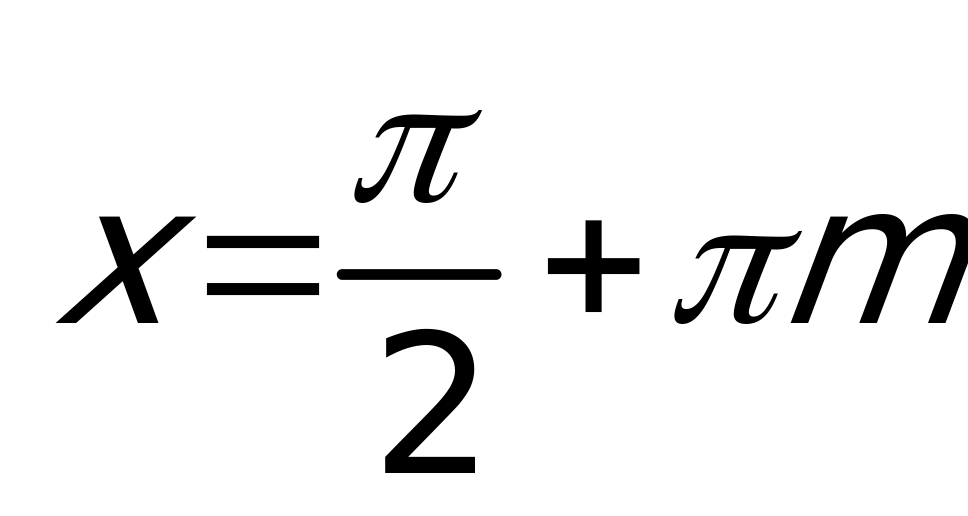 – тоже корни, которые мы потеряли, перейдя только к
– тоже корни, которые мы потеряли, перейдя только к 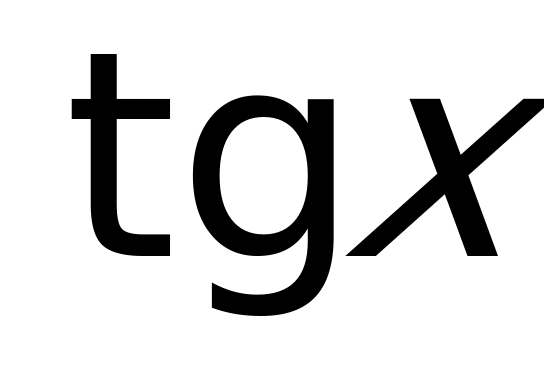 .
.
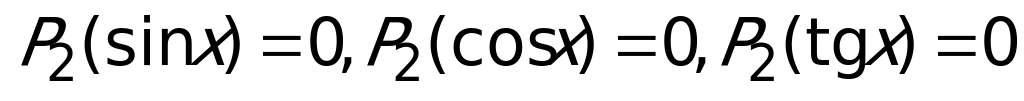
Пример 6. 
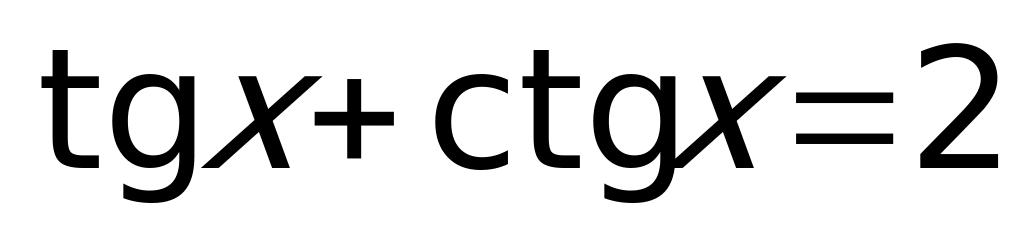
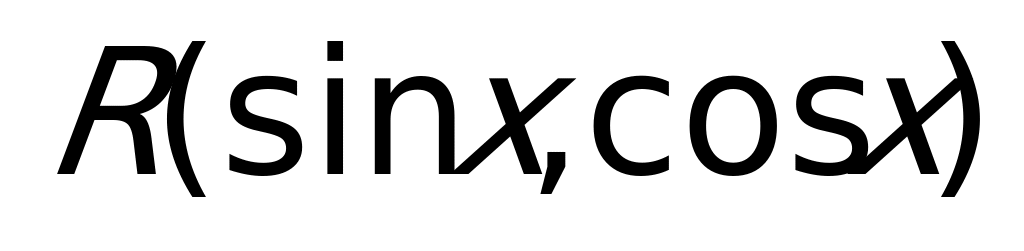 – выражение, получающееся из
– выражение, получающееся из 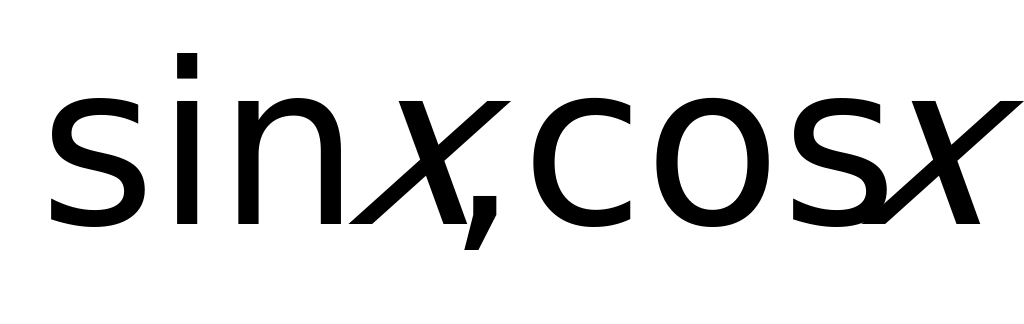 и действительных констант с помощью четырех действий арифметики.
и действительных констант с помощью четырех действий арифметики.

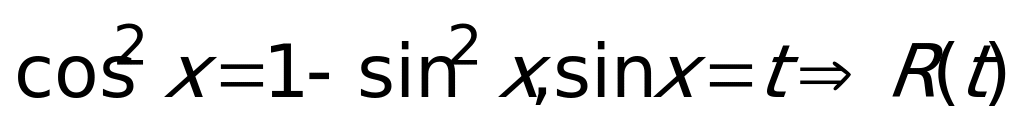
Пример 7. 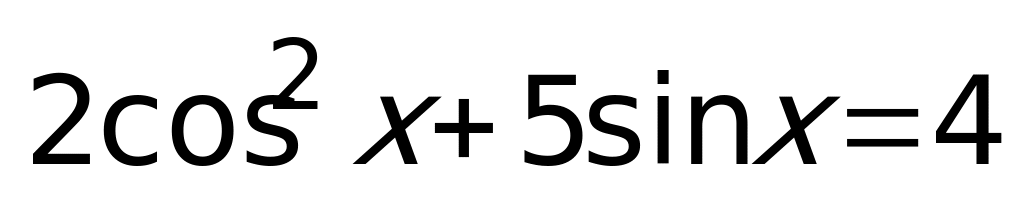
Решение: 
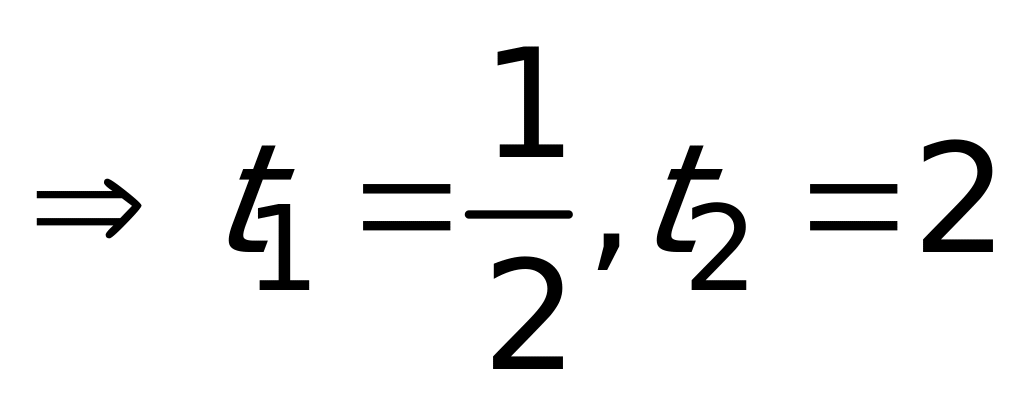
Ответ: 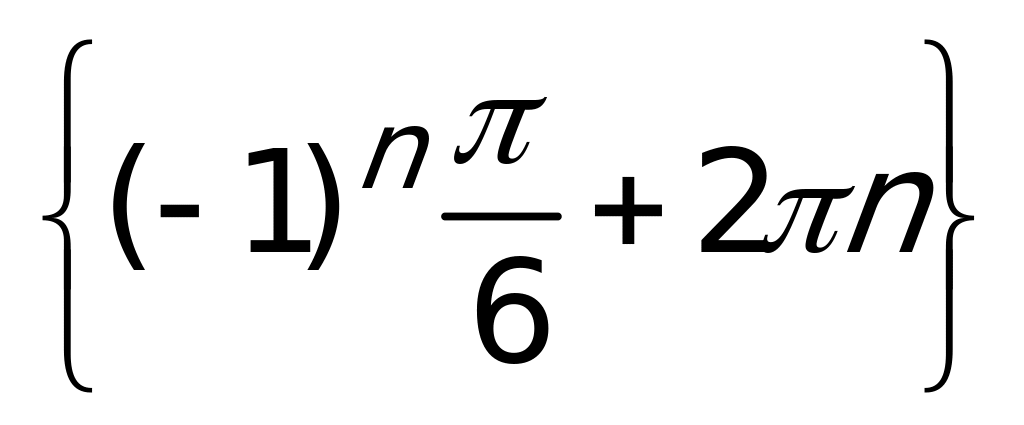 .
.
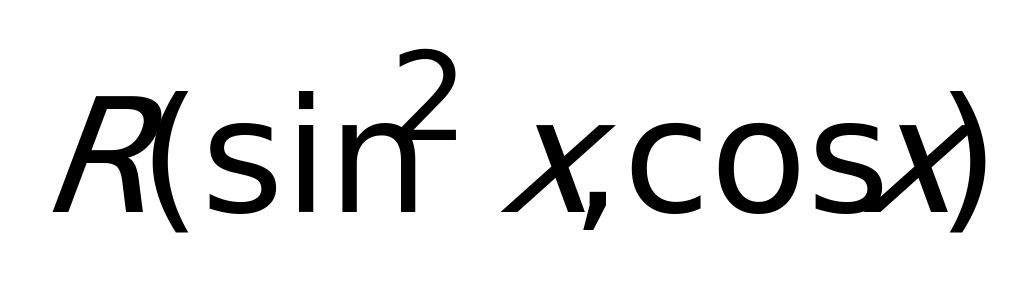 – аналогично.
– аналогично.
 – однородное 1-й ст.
– однородное 1-й ст. 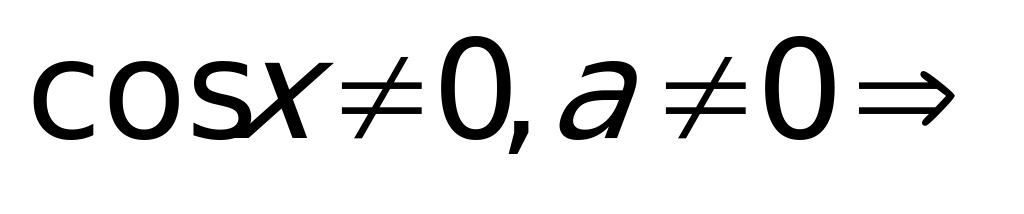 делим на
делим на 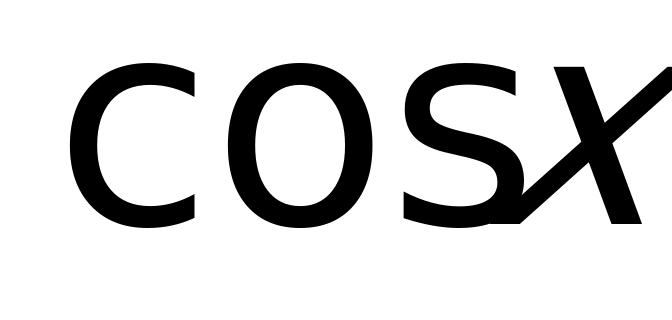 , получаем:
, получаем: 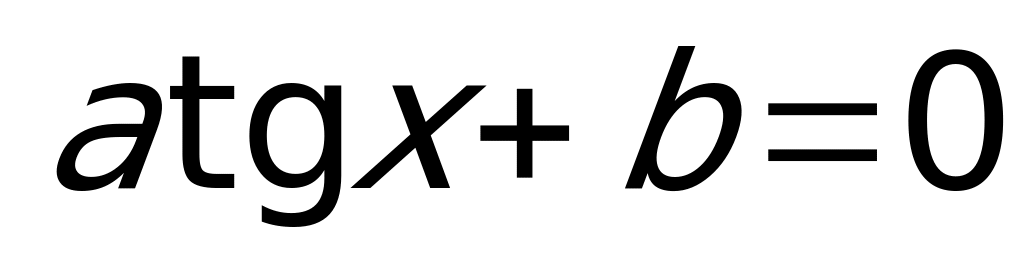 ,
, 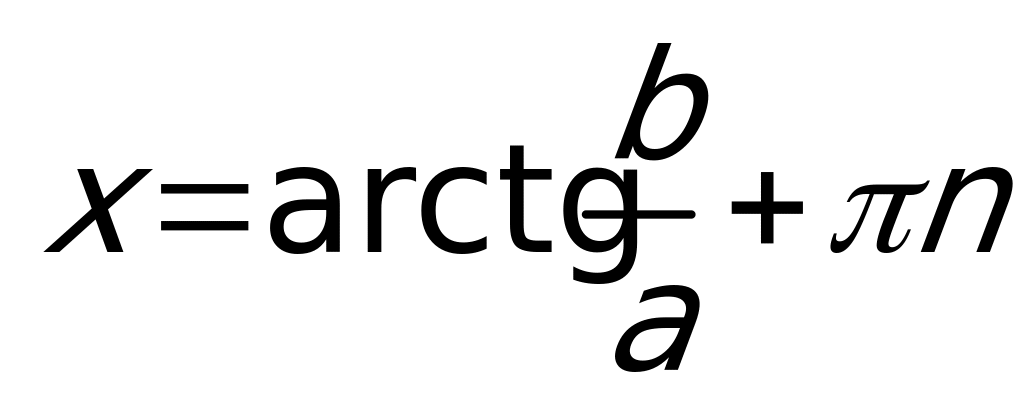 .
.
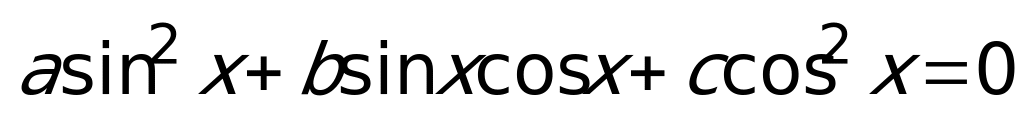 – однородное 2-й ст.
– однородное 2-й ст. 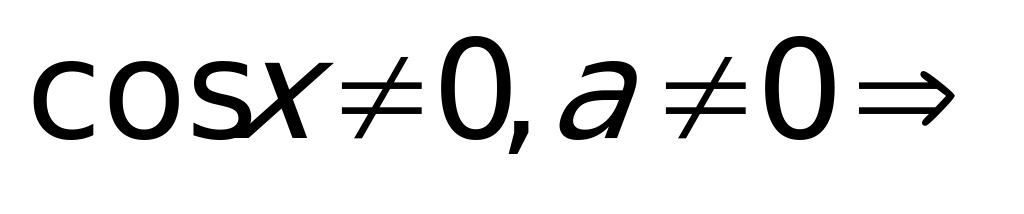 делим на
делим на 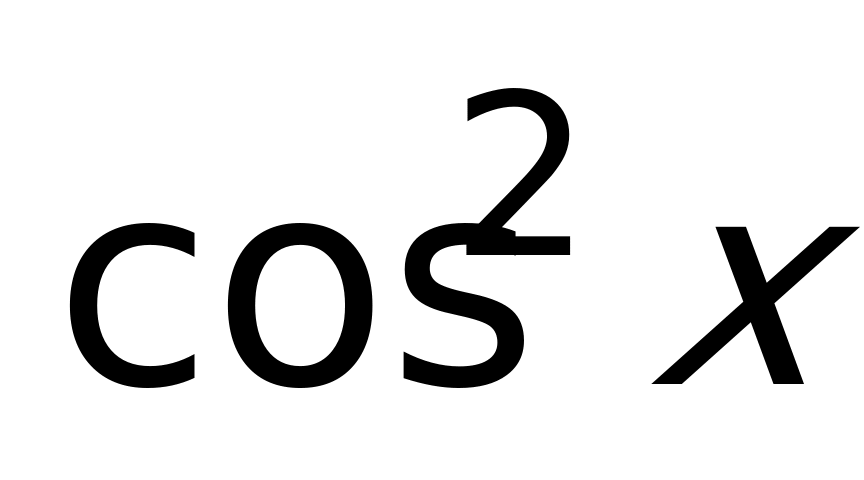 , получаем:
, получаем: 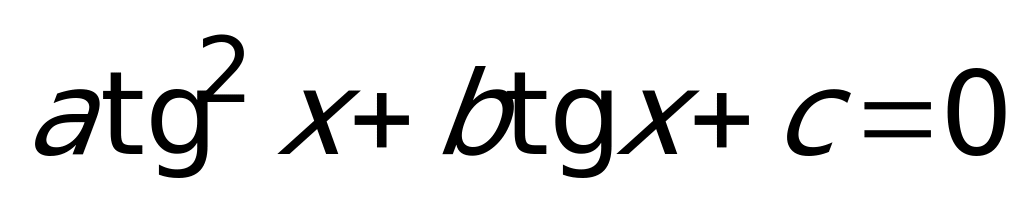 ,
, 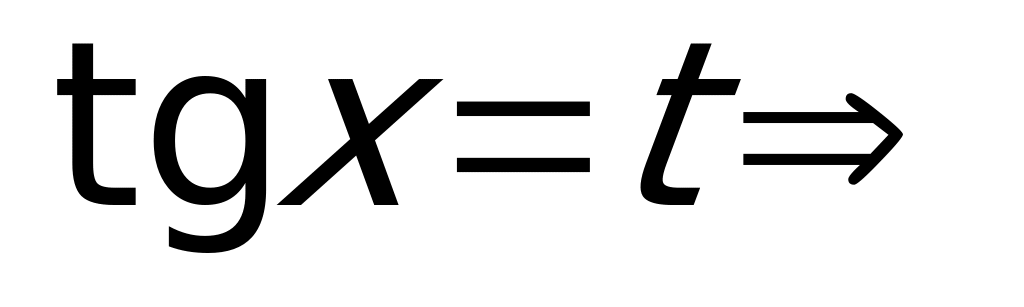
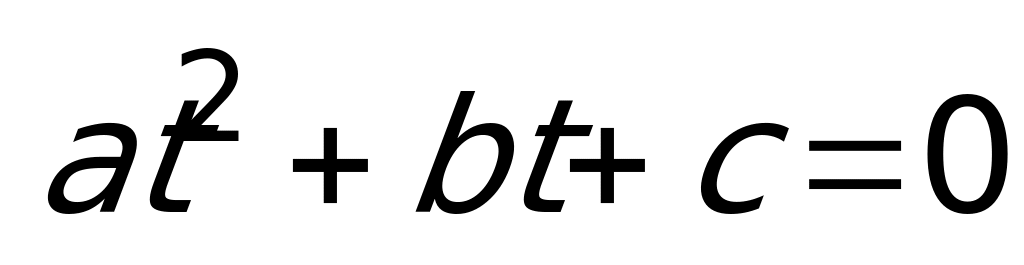
Пример 8. 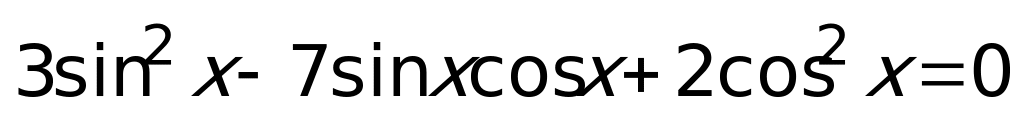
Ответ: 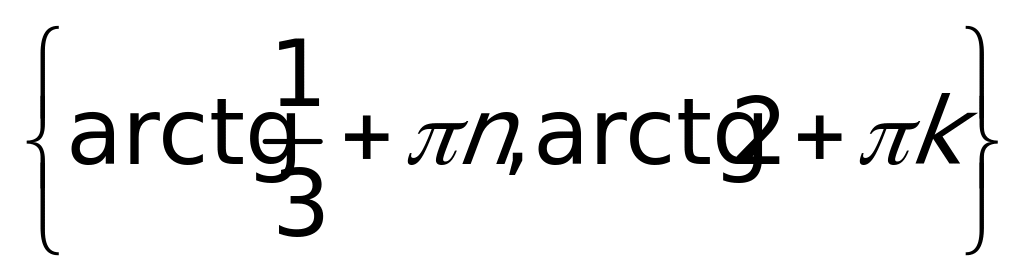
Замечание: Любое уравнение 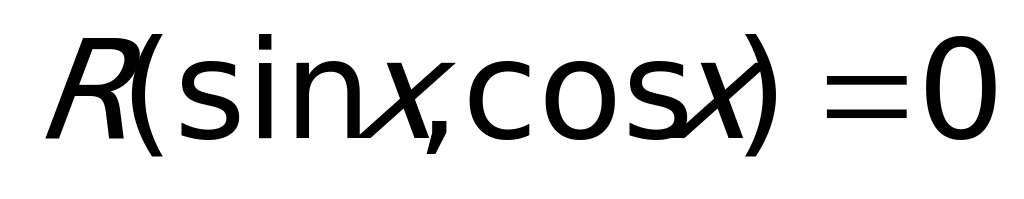 с помощью замены через
с помощью замены через 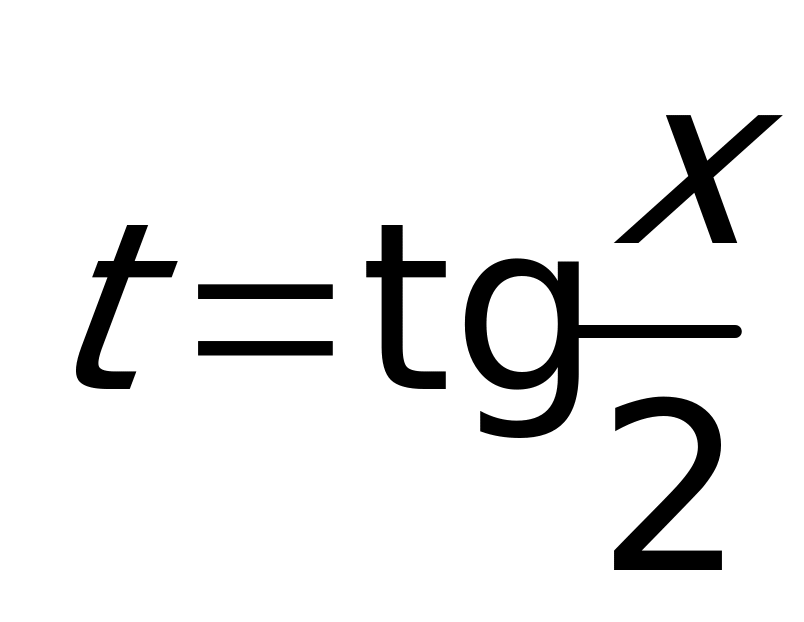 сводится к уравнению, рациональному относительно
сводится к уравнению, рациональному относительно 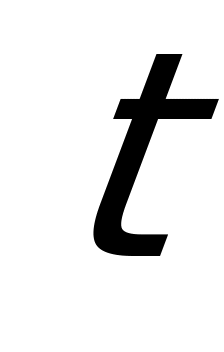 (не забыть проверить
(не забыть проверить 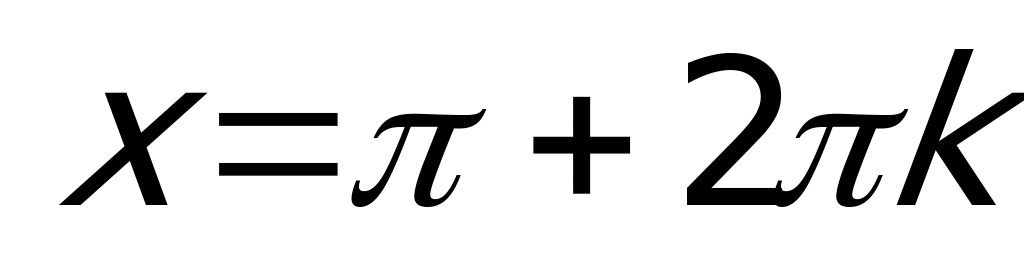 ). Поэтому такая подстановка называется универсальной.
). Поэтому такая подстановка называется универсальной.
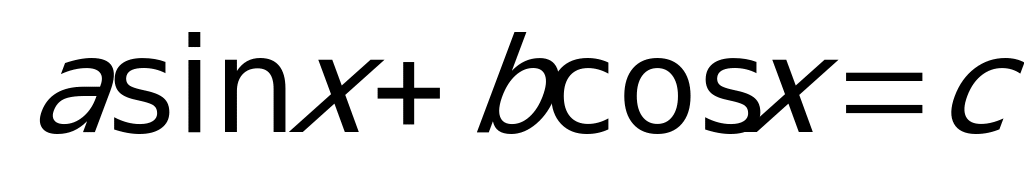
Способ 1: Метод дополнительного угла.
Разделив обе части уравнения на величину 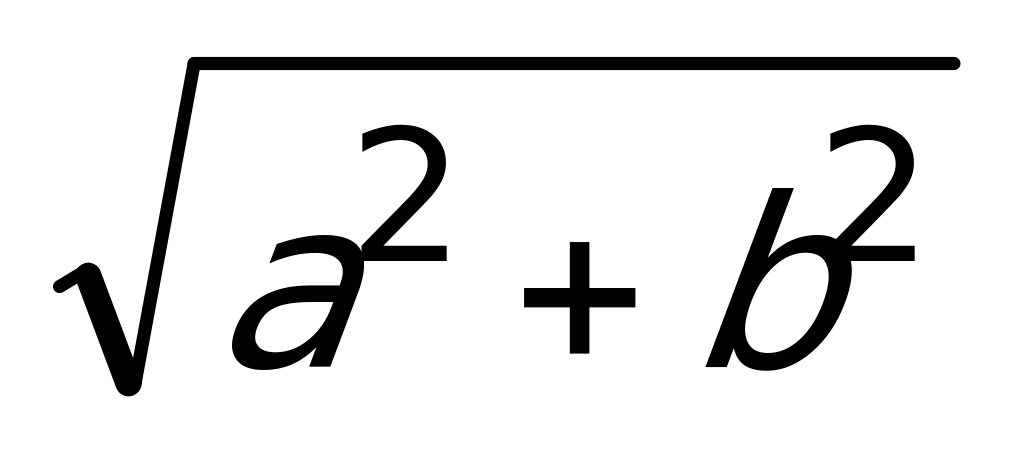 , получим уравнение
, получим уравнение 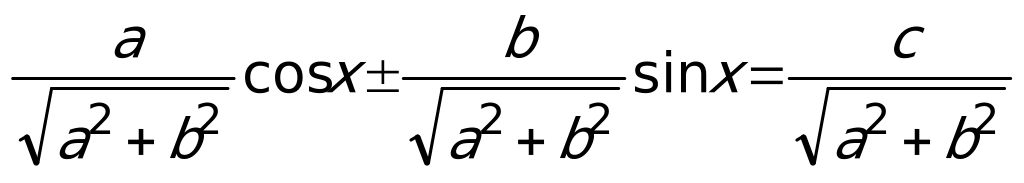 . Введем дополнительный острый угол
. Введем дополнительный острый угол 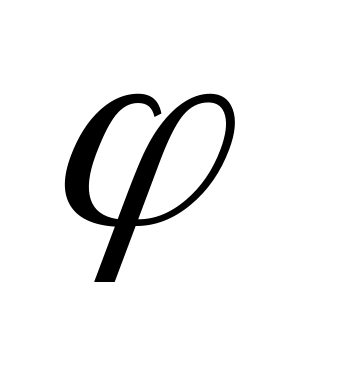 , исходя из условий:
, исходя из условий: 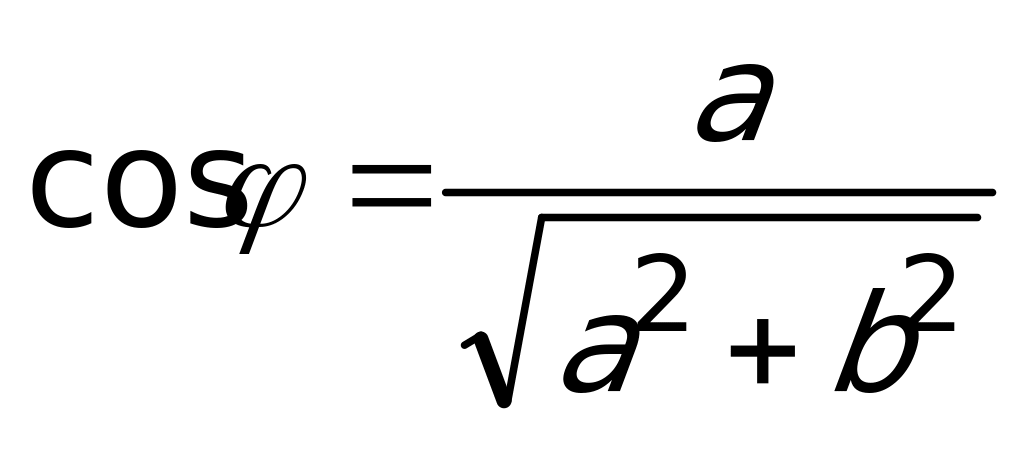 и
и 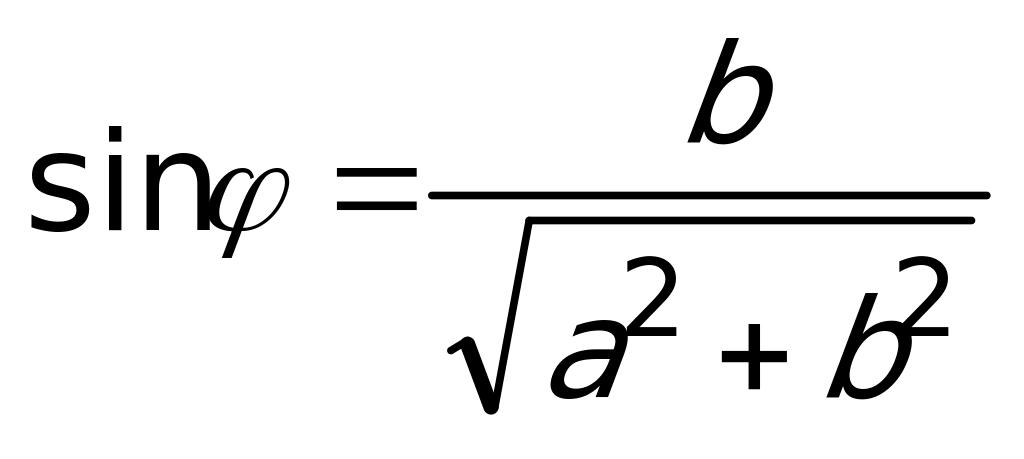 . К полученному после этих преобразований уравнению
. К полученному после этих преобразований уравнению 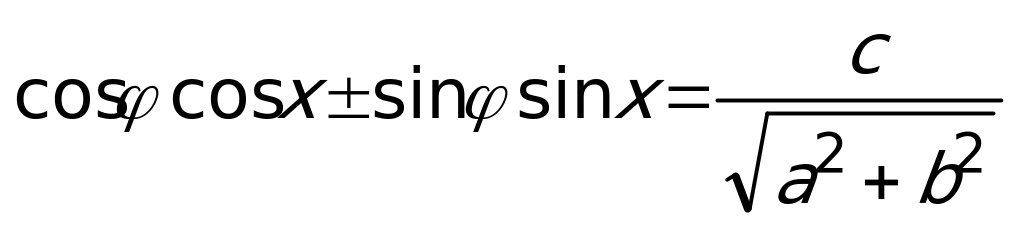 применим формулу косинуса разности или суммы аргументов. Имеем:
применим формулу косинуса разности или суммы аргументов. Имеем: 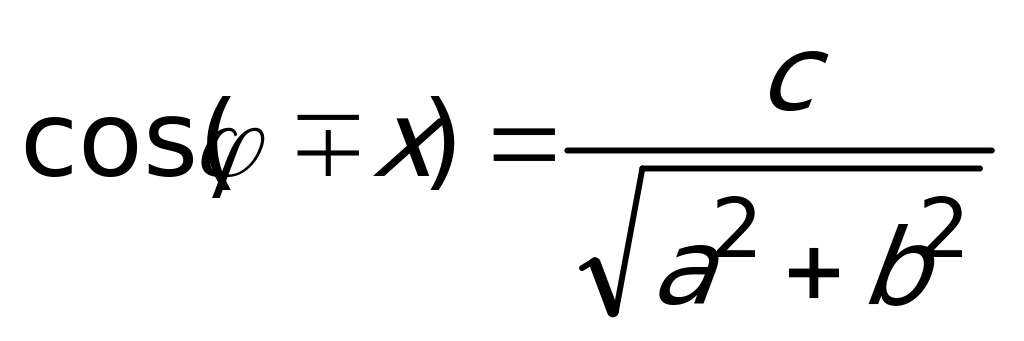 . Последнее уравнение решается по стандартным формулам.
. Последнее уравнение решается по стандартным формулам.
Способ 2: Так как 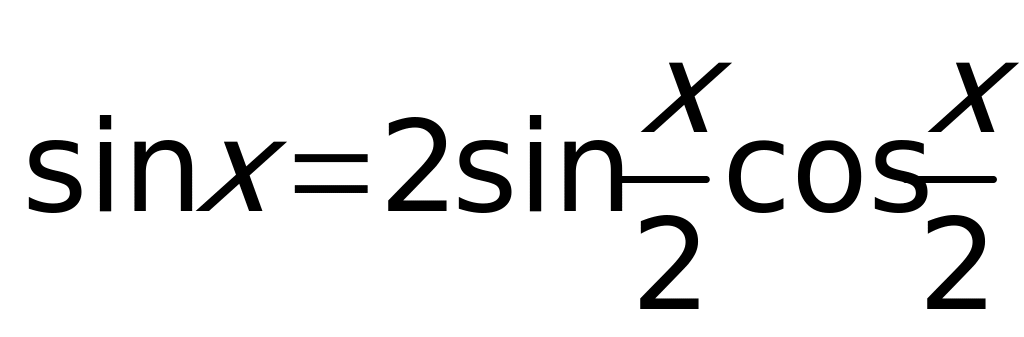 ,
, 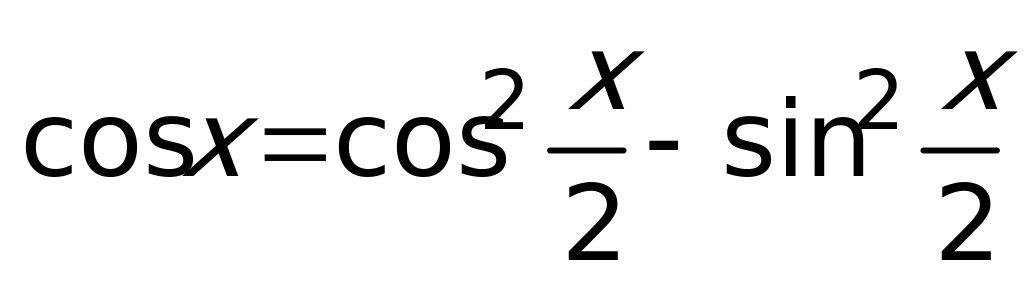 ,
, 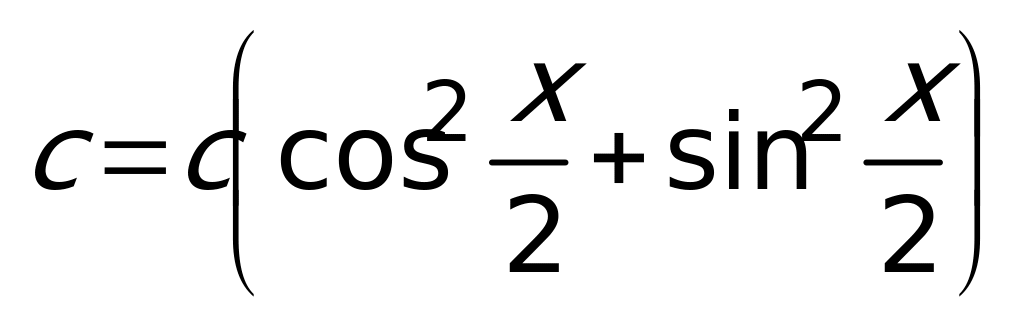 , то уравнение можно переписать в виде:
, то уравнение можно переписать в виде: 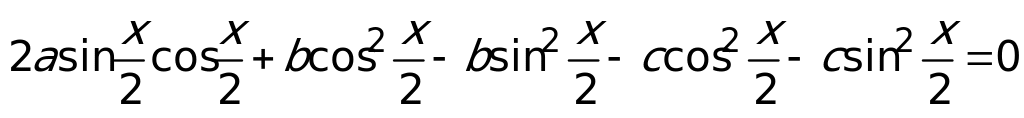 .
.
Это однородное уравнение 2-й степени, которое после приведения подобных членов решается соответствующим способом. Заметим, что этого же результата можно достичь сразу, используя универсальную подстановку.
Пример 9.  .
.
Решение: 1 способ: разделив обе части уравнения на 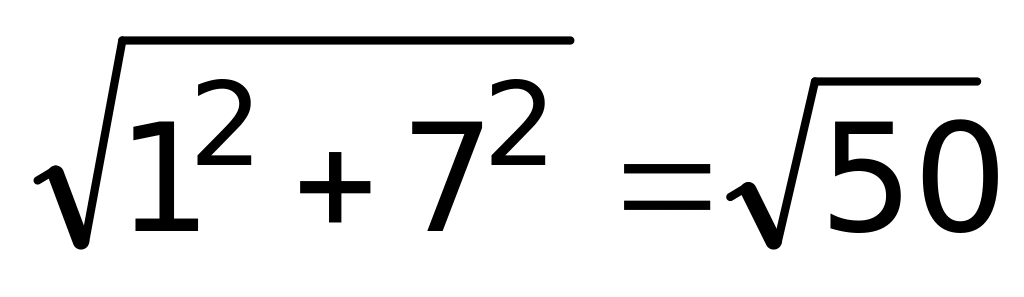 , получим
, получим  . Теперь уравнение можно переписать в виде:
. Теперь уравнение можно переписать в виде: 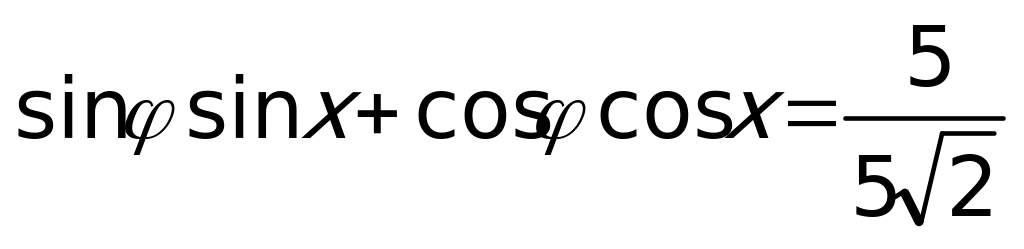 или
или 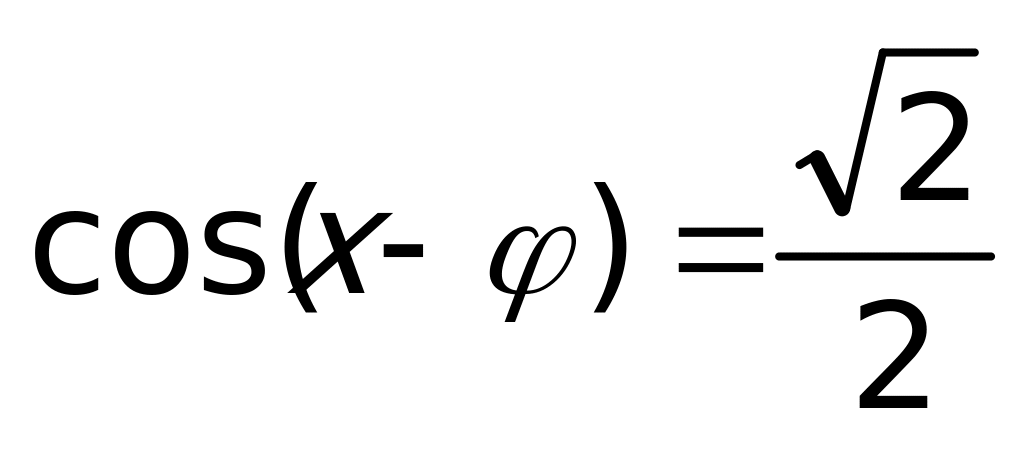 , где
, где  . Далее:
. Далее: 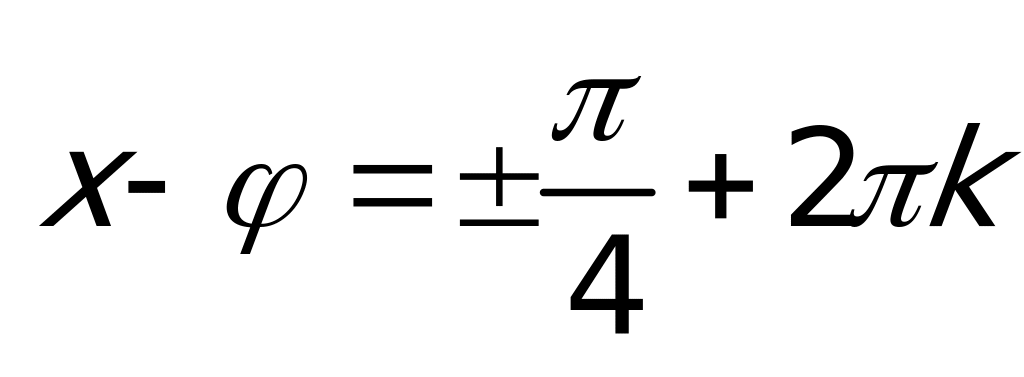 , или, выражая х,
, или, выражая х, 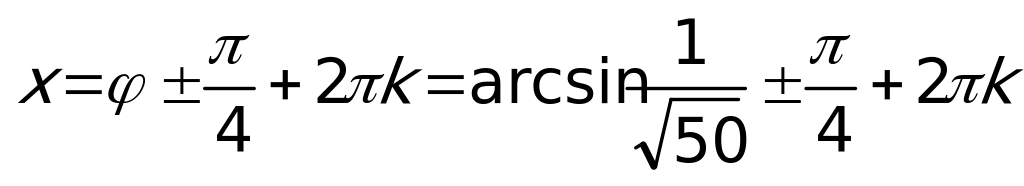 .
.
Ответ: 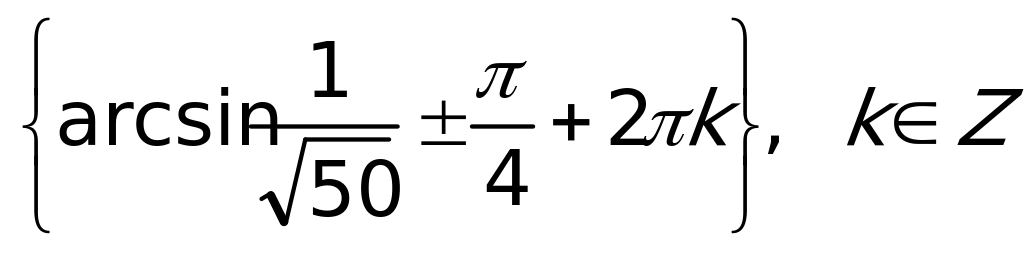 .
.
2 способ: 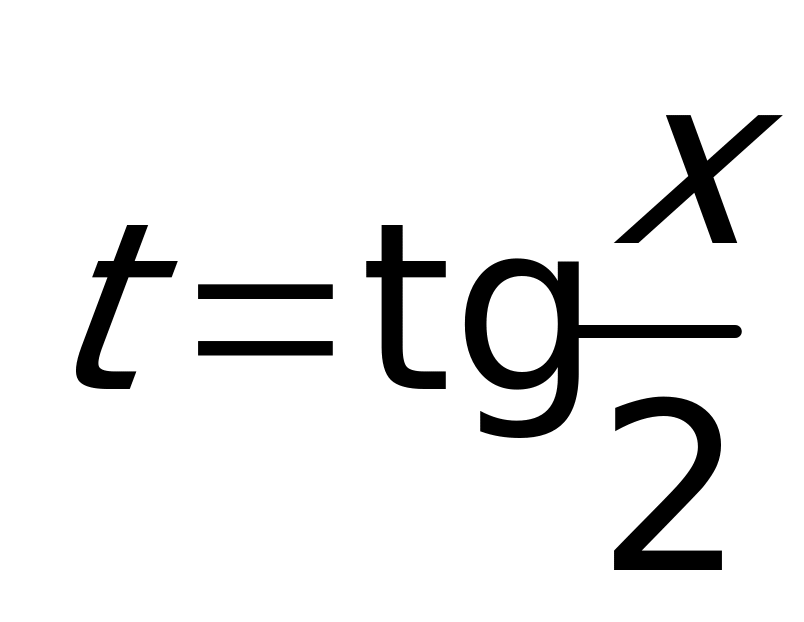 ,
, 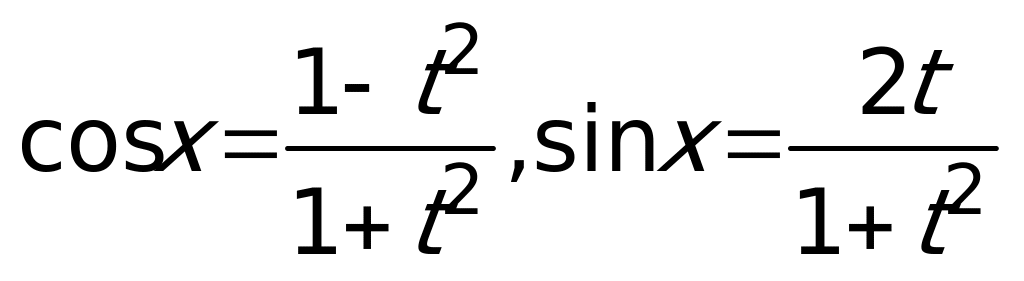
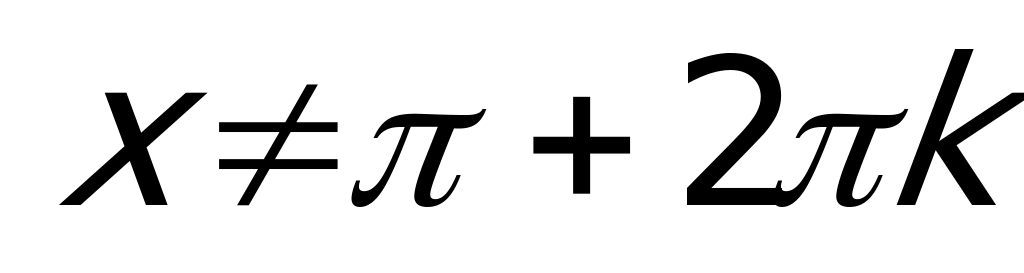
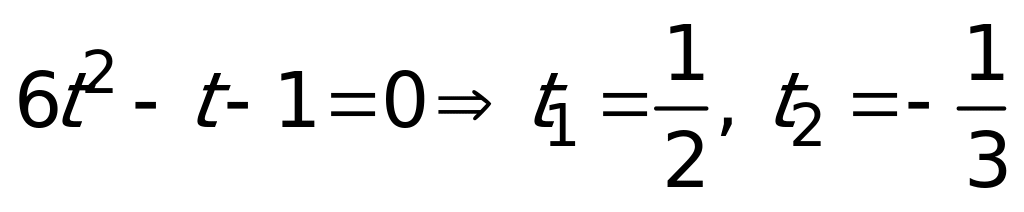
Ответ: 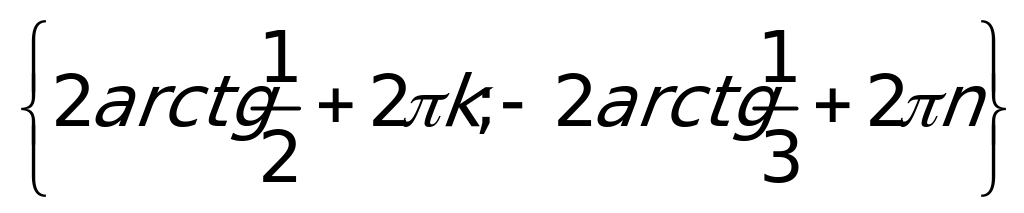
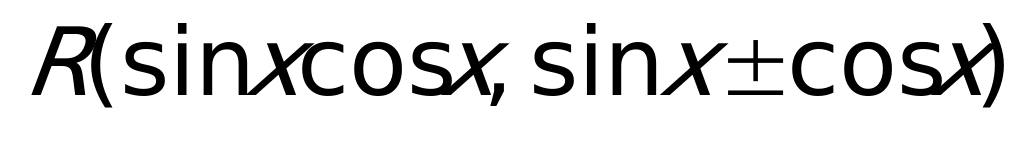
Решаются заменой 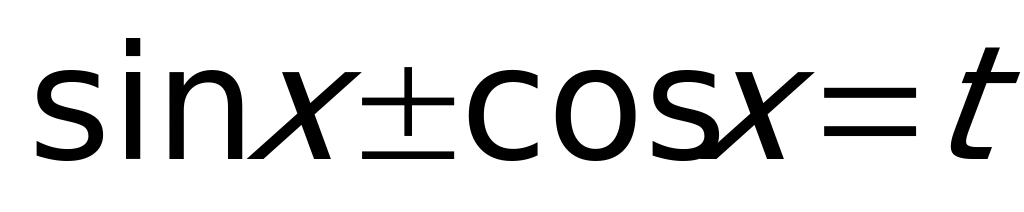 .
.
Чтобы выразить произведение функций, возведем равенство в квадрат, получим 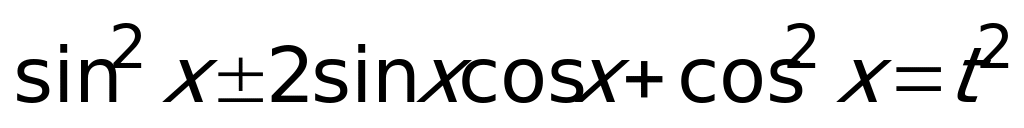 или
или 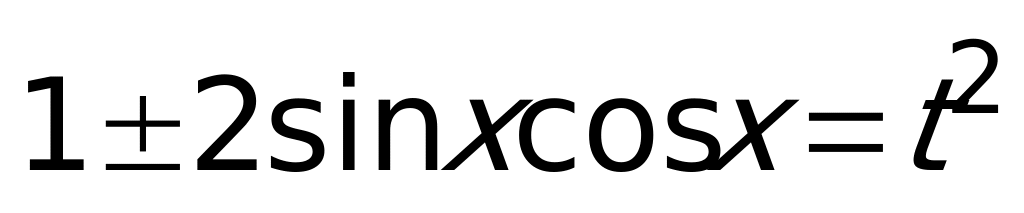 , откуда
, откуда  .
.
Пример 10. 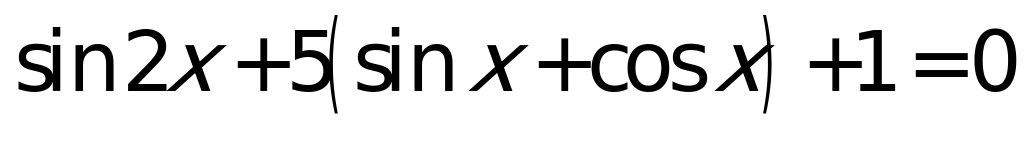
Решение: 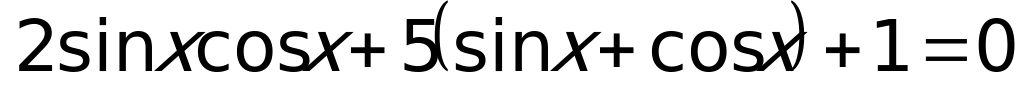 Сделаем замену
Сделаем замену 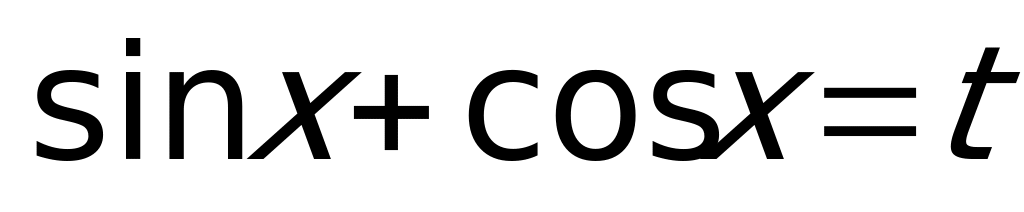 , откуда
, откуда 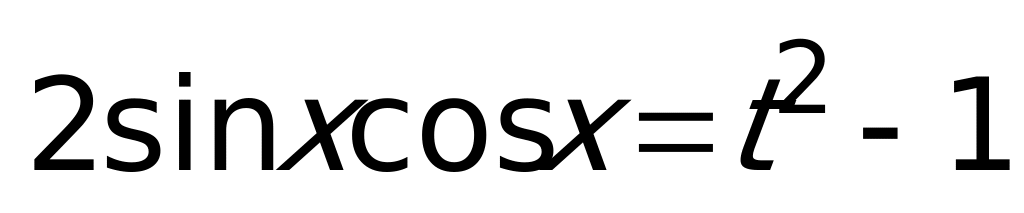 . Получаем уравнение
. Получаем уравнение 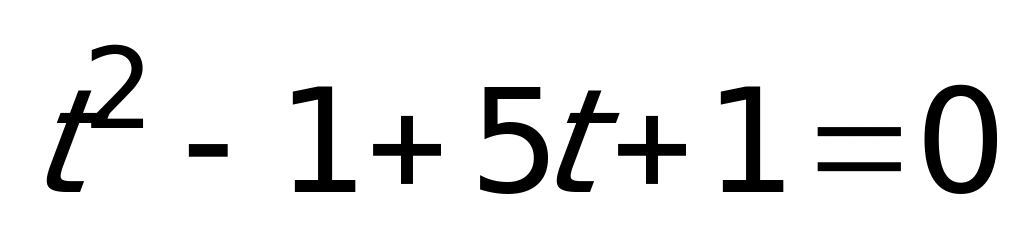 с корнями
с корнями 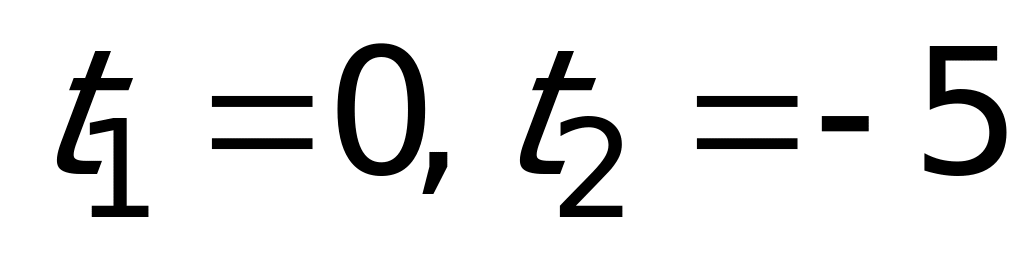 . Делаем обратную замену:
. Делаем обратную замену: 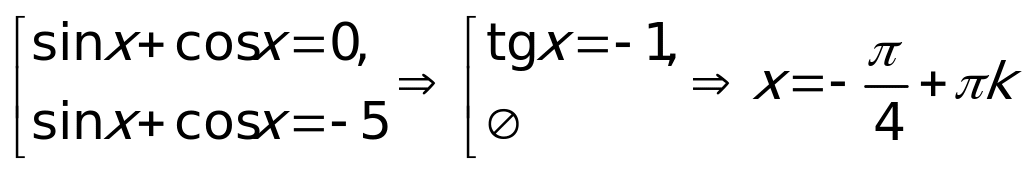 .
.
Ответ:  .
.
Пример 11.  .
.
Решение: ОДЗ: 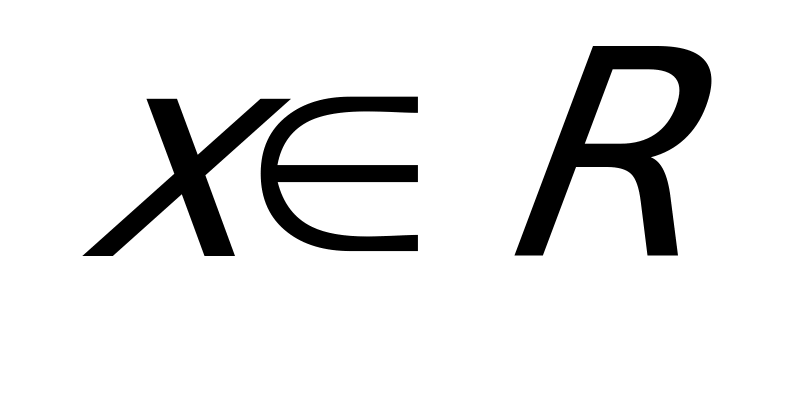 . Так как
. Так как 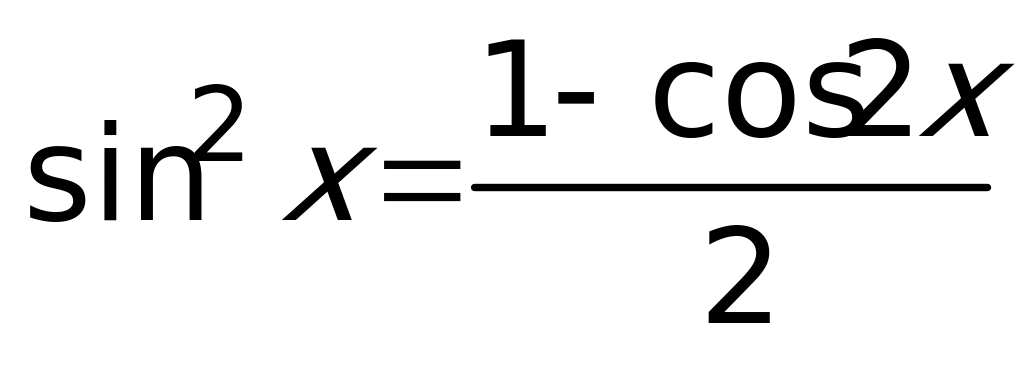 , имеем:
, имеем: 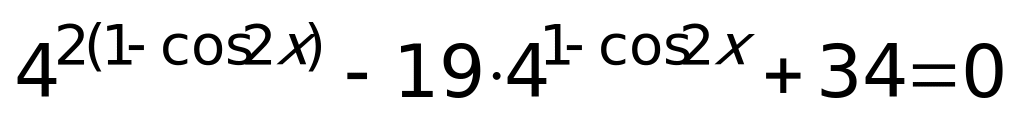 .Пусть
.Пусть 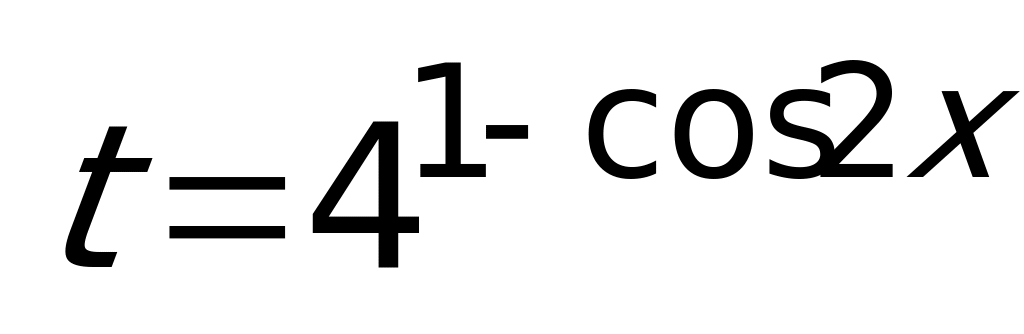 , тогда
, тогда 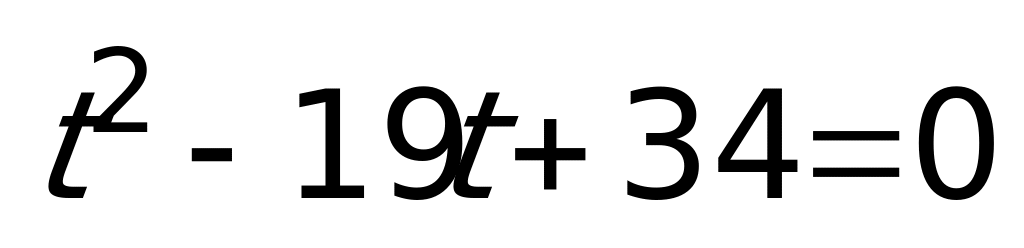
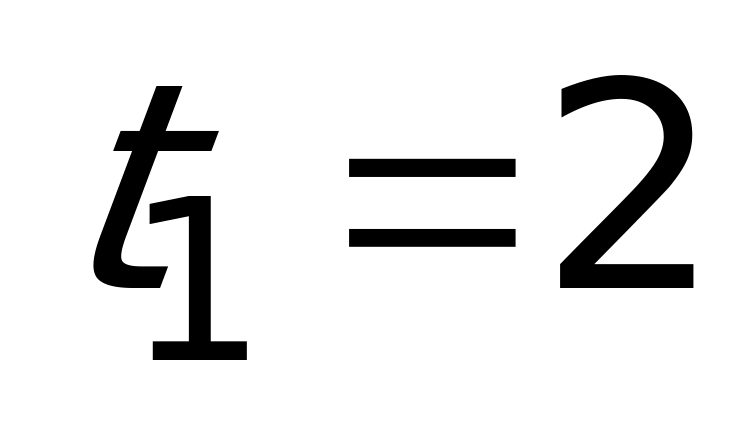 ,
, 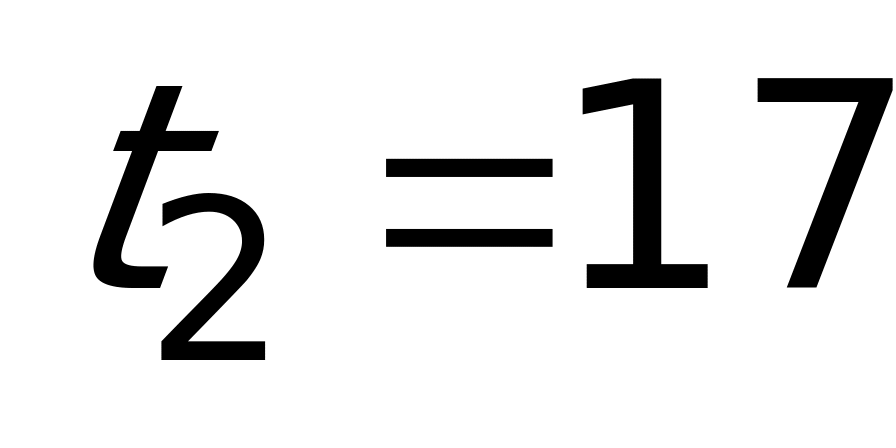 .
.
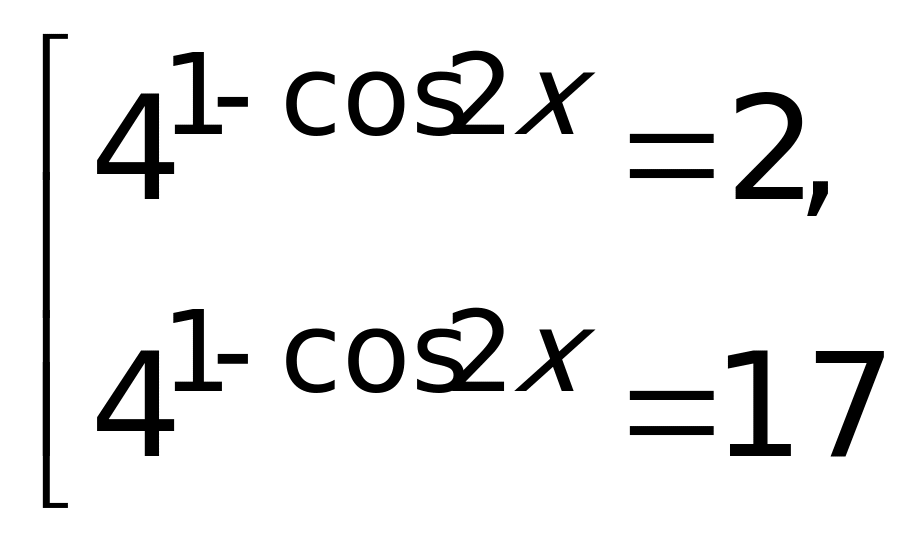
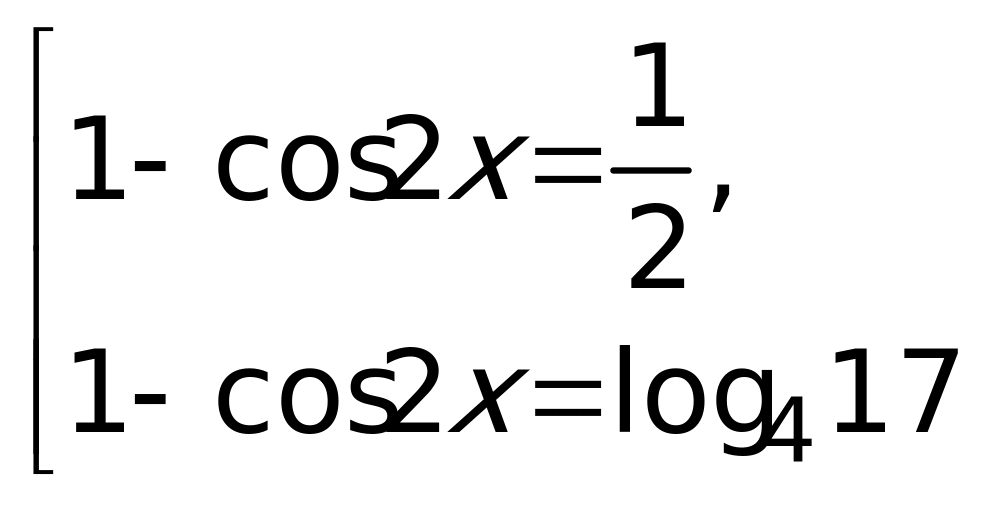
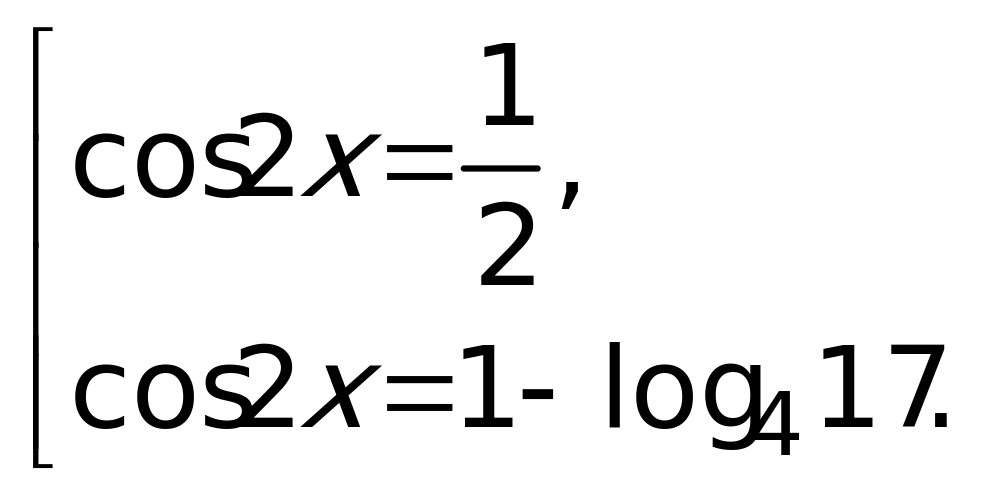
Второе уравнение полученной совокупности решений не имеет, так как 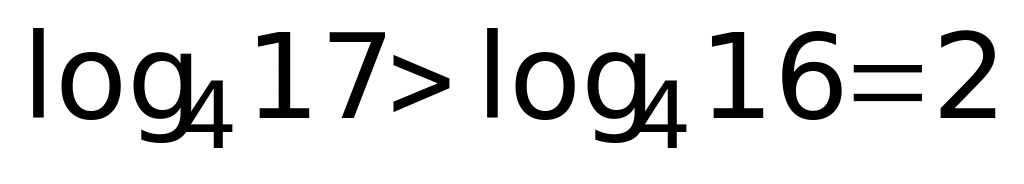 , а, следовательно,
, а, следовательно, 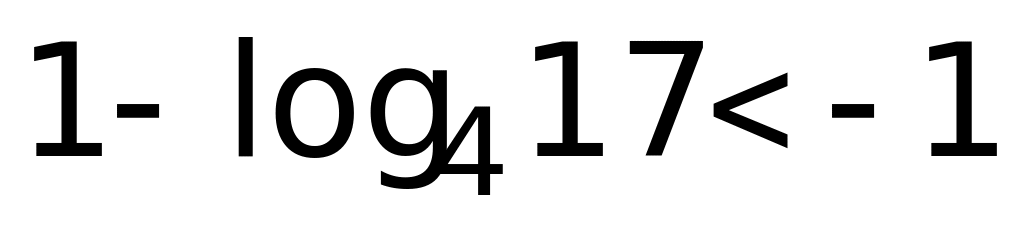 . Решая первое уравнение совокупности, получаем:
. Решая первое уравнение совокупности, получаем: 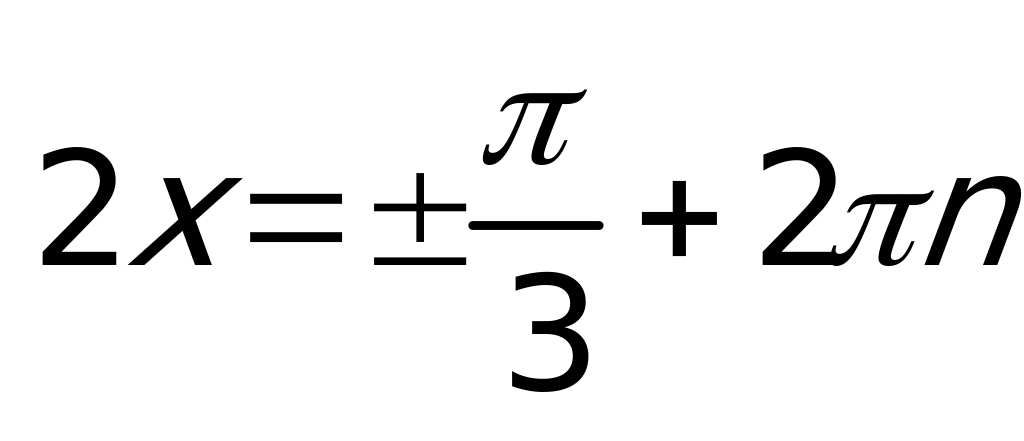 или
или 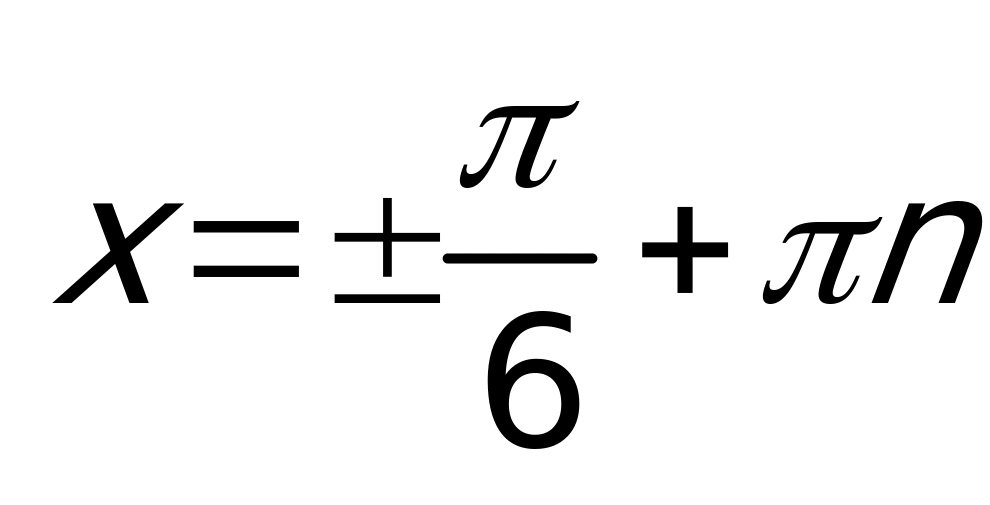 .
.
Ответ: 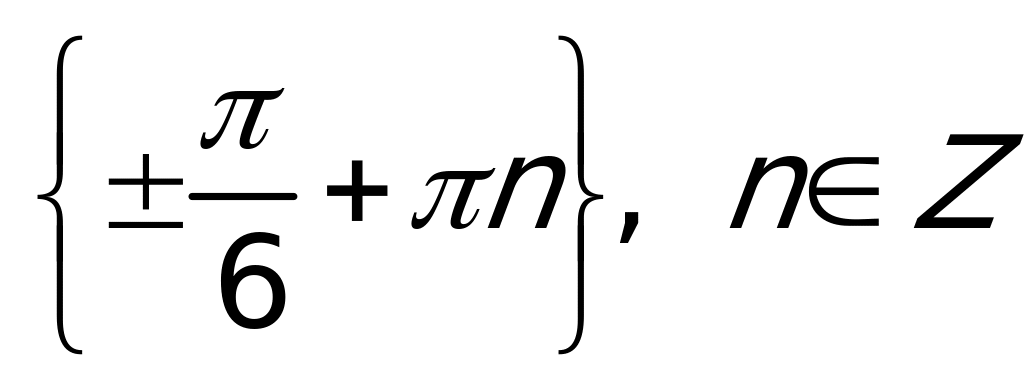 .
.
Основные типы тригонометрических уравнений.
Уравнения 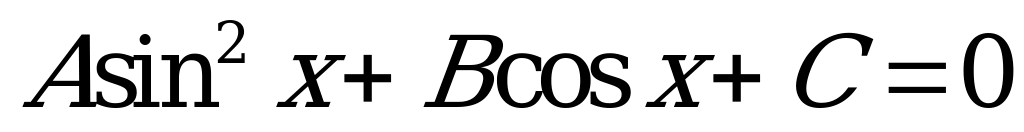 и
и 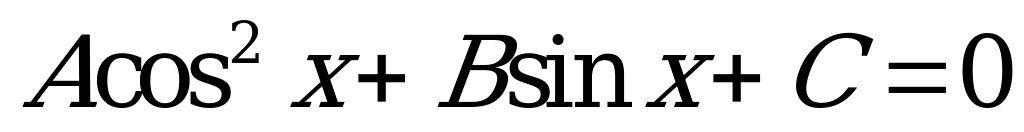 сводятся к квадратным относительно замены
сводятся к квадратным относительно замены 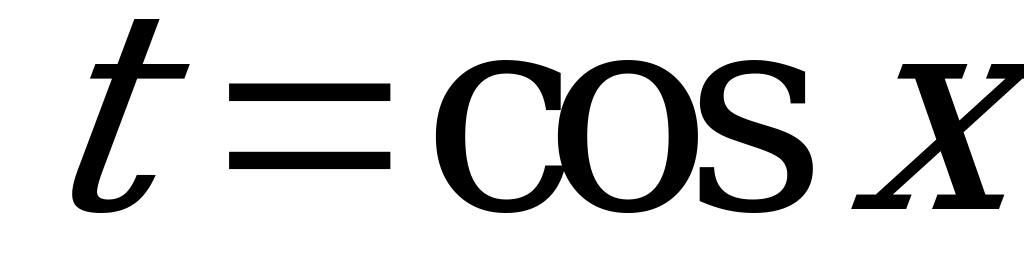 и
и 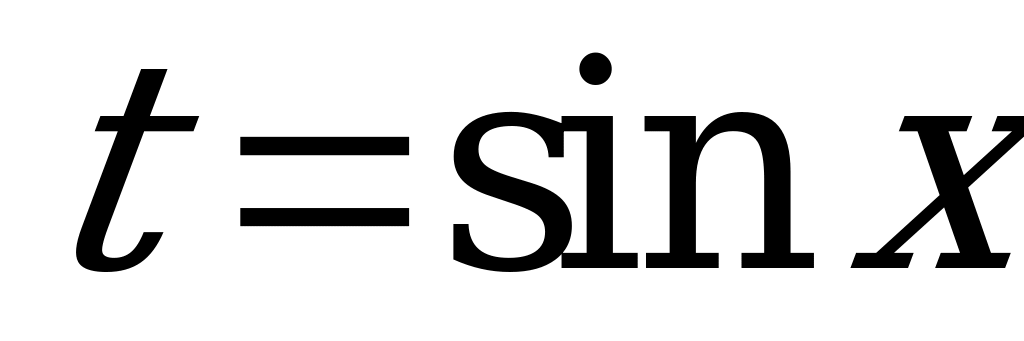 .
.
Однородное уравнение 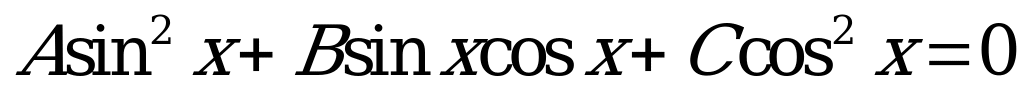 , где
, где 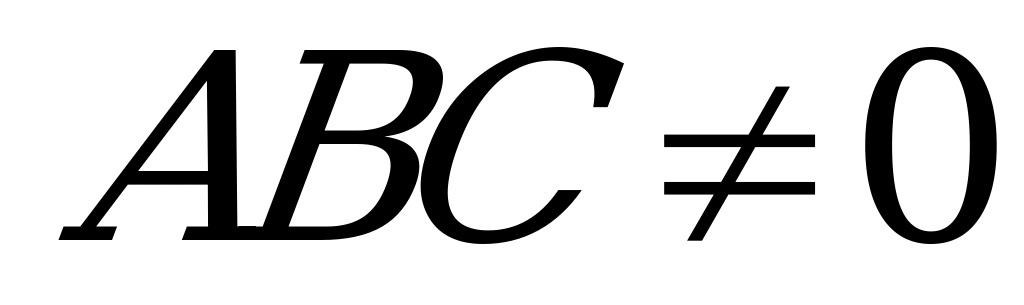 , равносильно уравнению
, равносильно уравнению  .
.
Уравнение 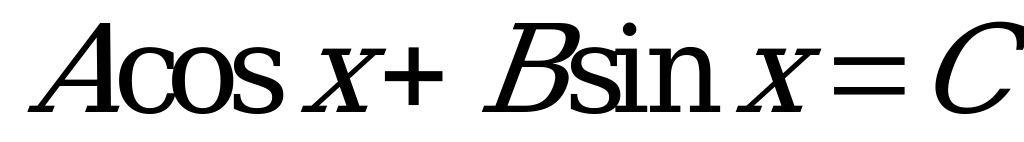 удобно записать в виде
удобно записать в виде 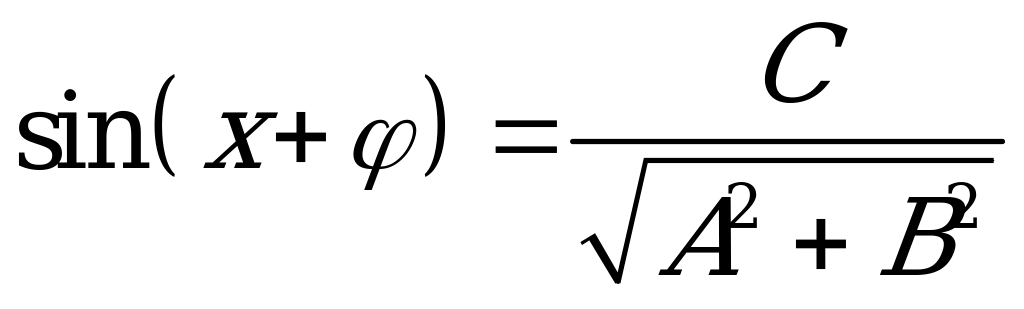 ; здесь
; здесь 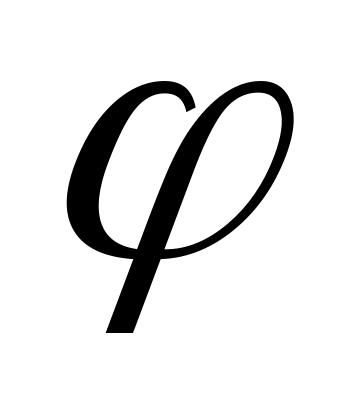 - вспомогательный угол, такой что
- вспомогательный угол, такой что 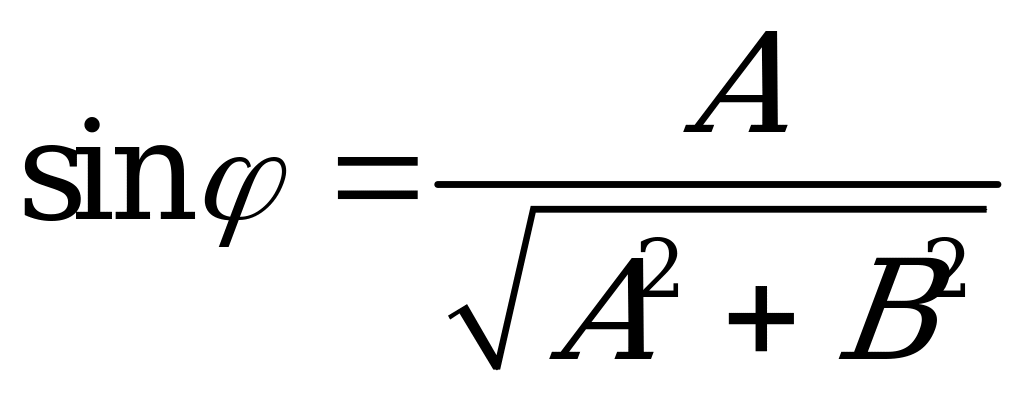 ,
, 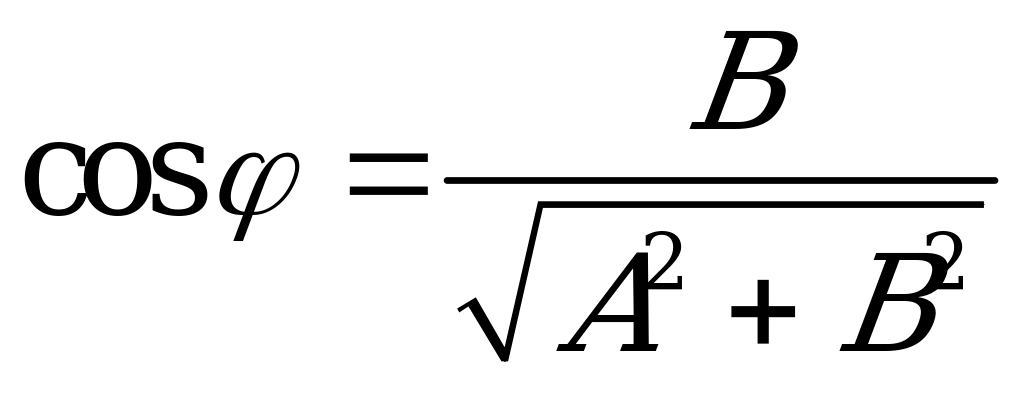 .
.
Уравнения 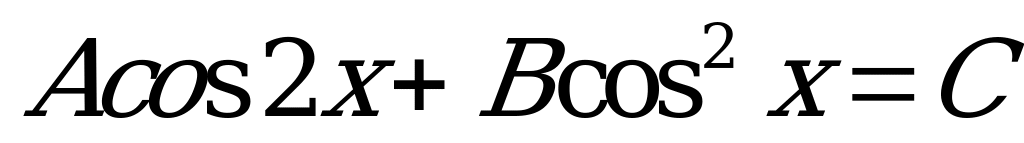 и
и 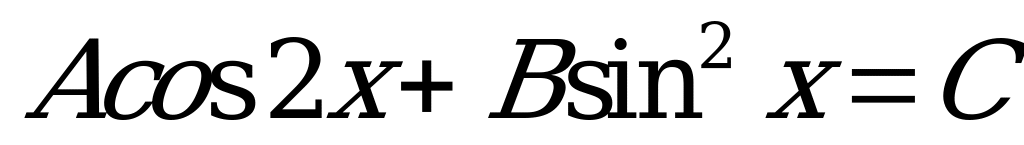 сводятся к уравнениям вида
сводятся к уравнениям вида 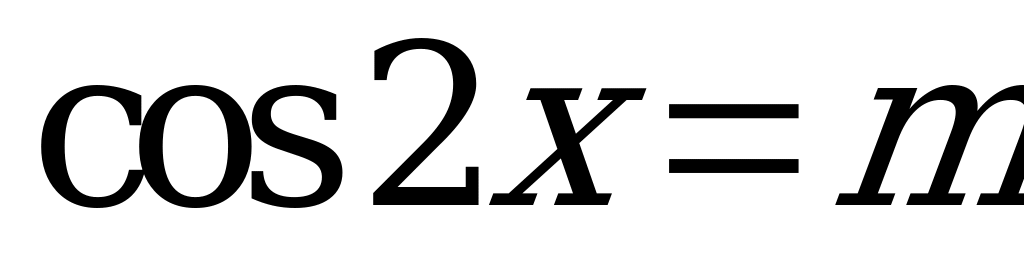
с помощью формул понижения степени: 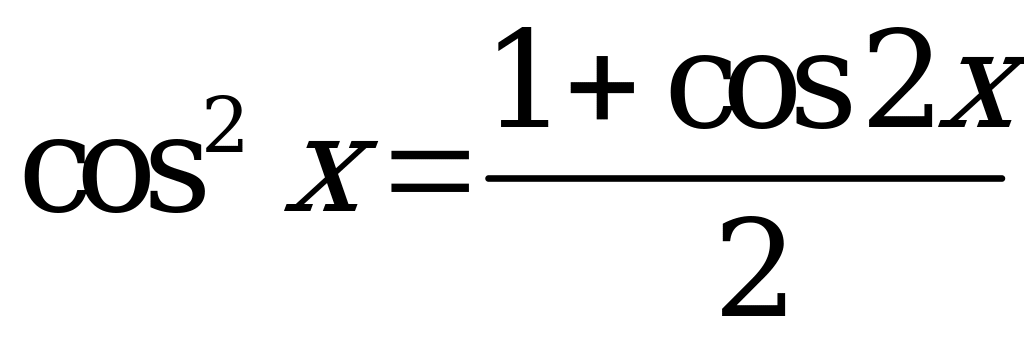 ;
; 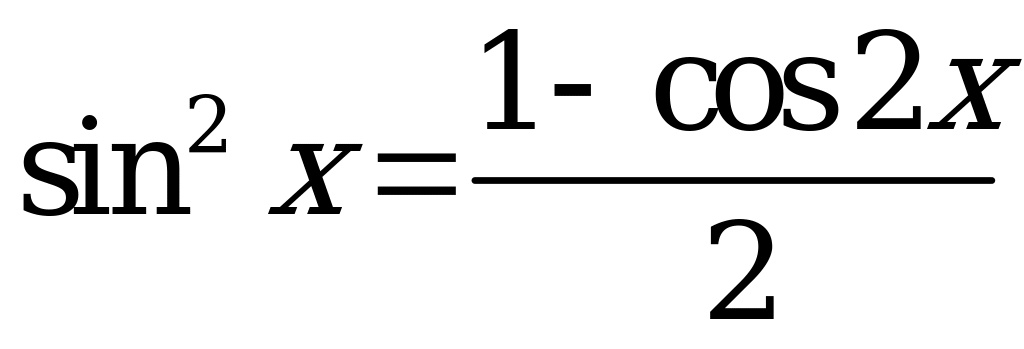 .
.
Уравнения 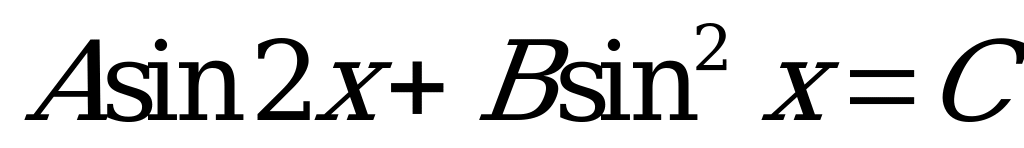 и
и  можно свести
можно свести
либо к однородным, используя тождество 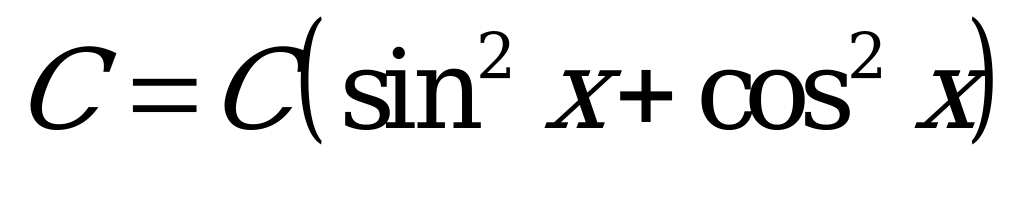 ,
,
либо к уравнениям вида 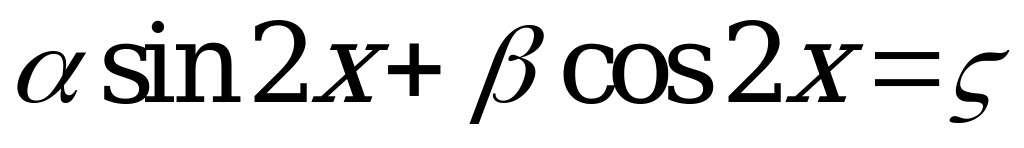 , используя формулы понижения степени.
, используя формулы понижения степени.
Уравнения 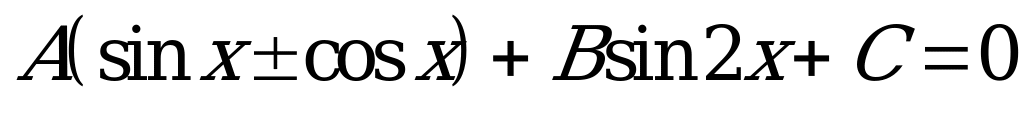 сводятся к квадратным относительно замены
сводятся к квадратным относительно замены 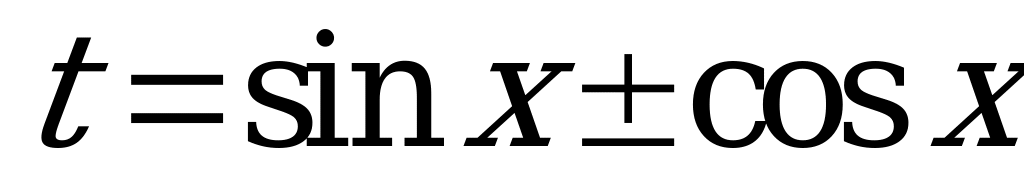 , т.к.
, т.к. 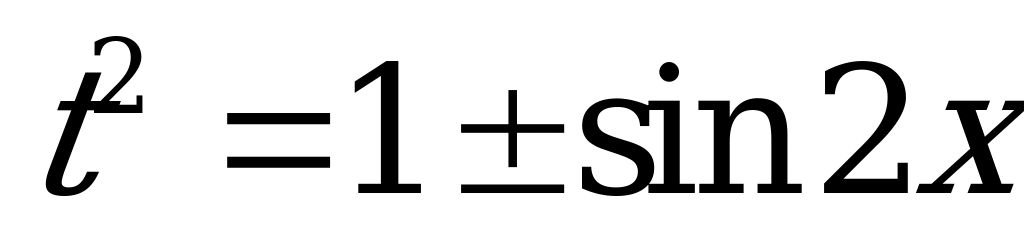 .
.
Пример 1. Найти число корней уравнения 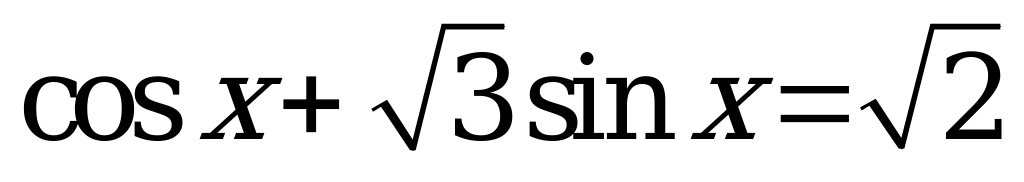 на интервале
на интервале 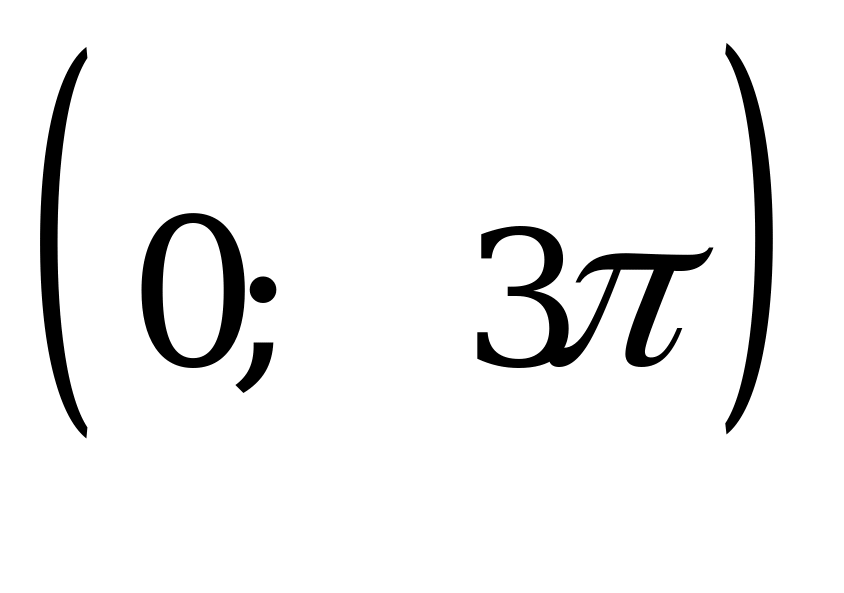 .
.
Решение. Это уравнение решается методом введения вспомогательного аргумента. Разделив обе части уравнения на 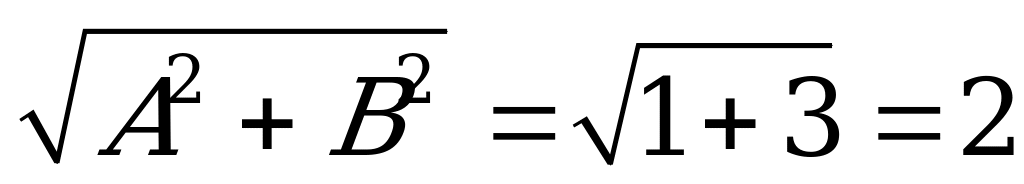 , получим
, получим 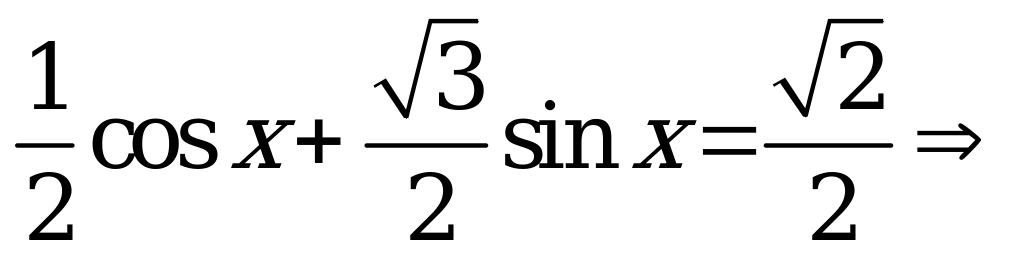
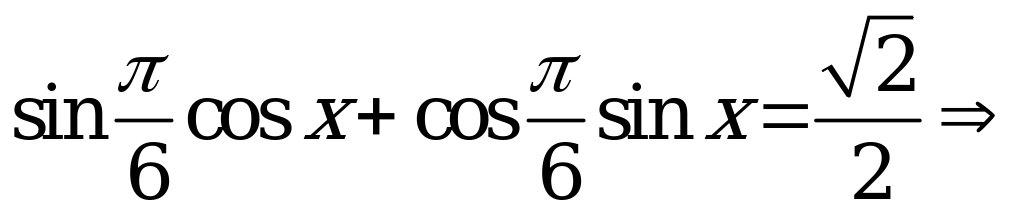
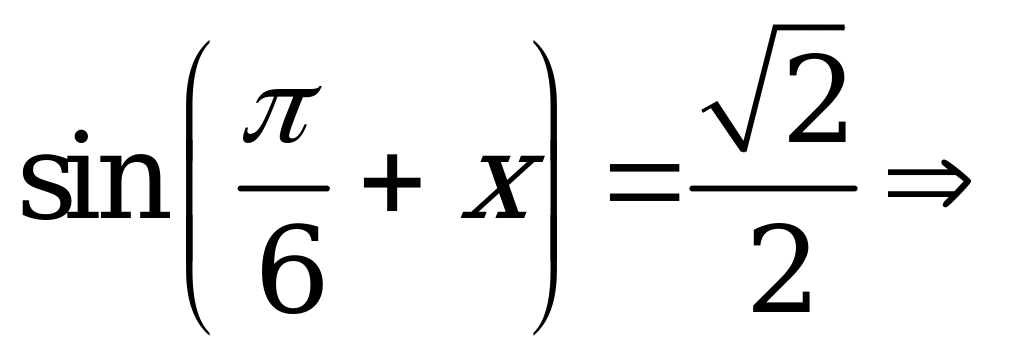
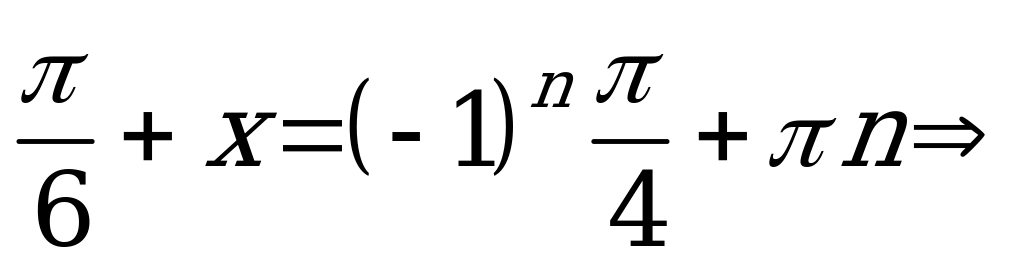
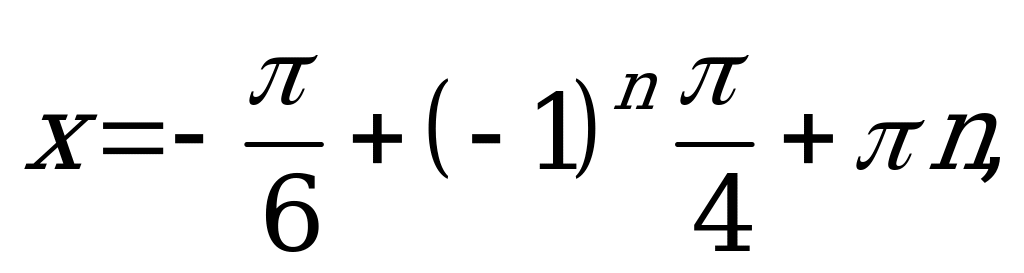
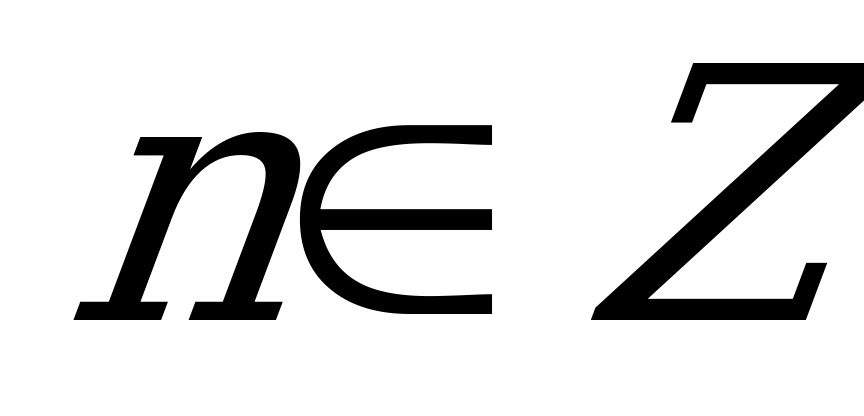 . Подсчитаем число корней, принадлежащих интервалу
. Подсчитаем число корней, принадлежащих интервалу 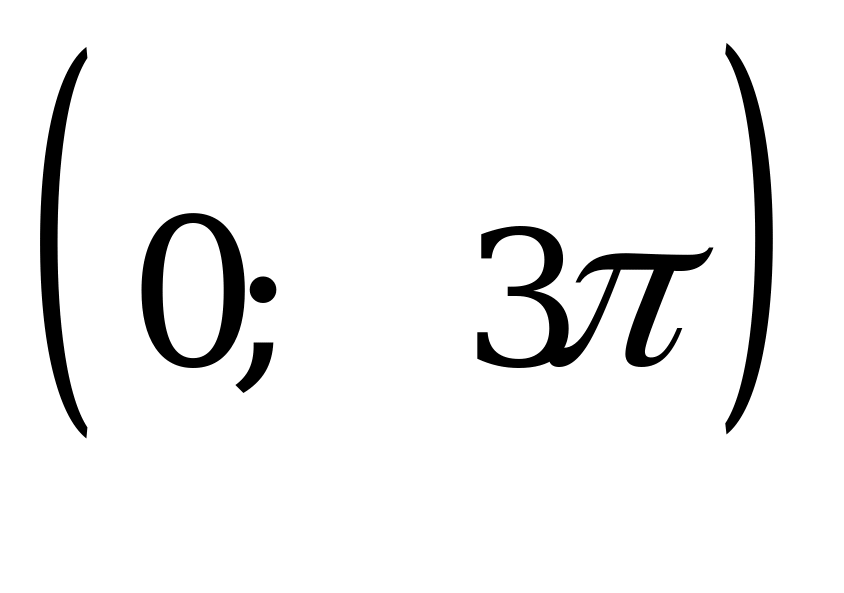 : при
: при 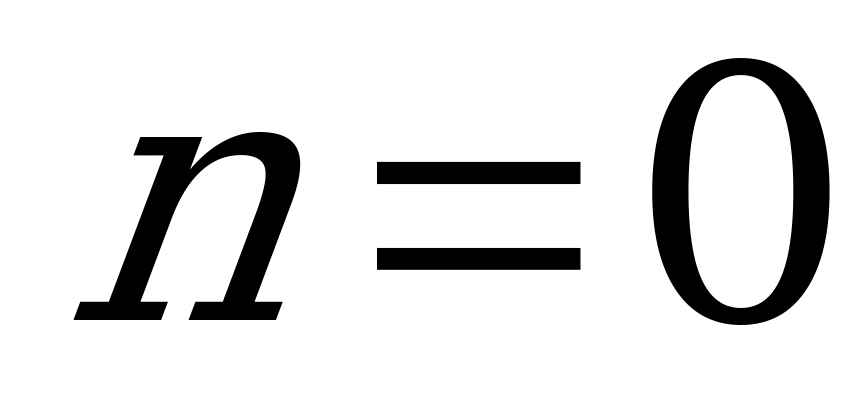
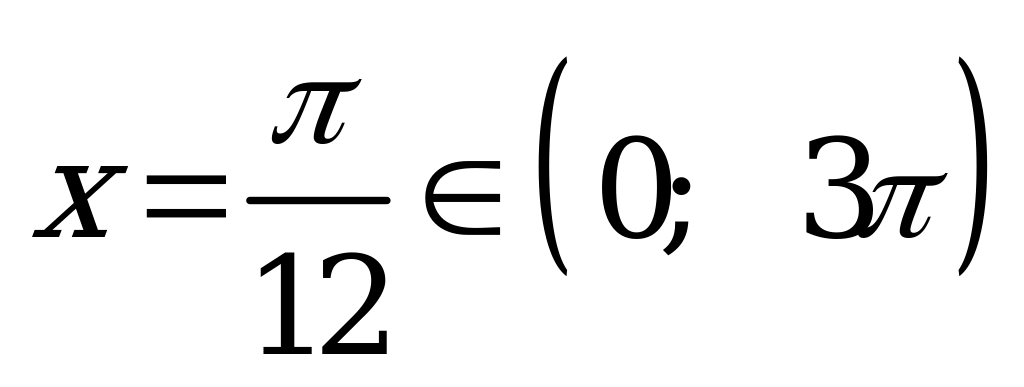 ;
;
при 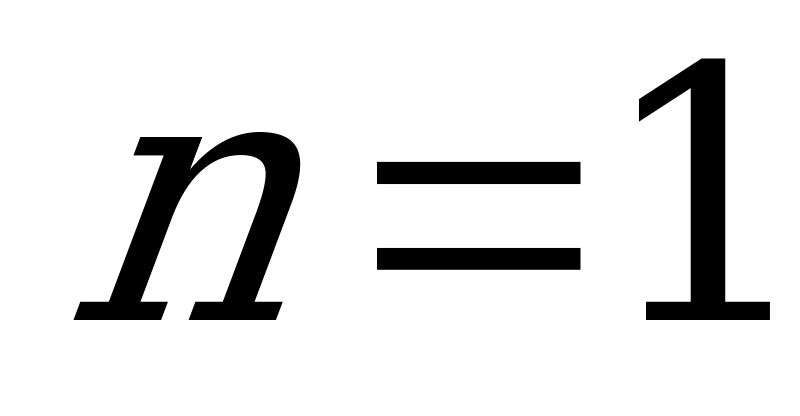
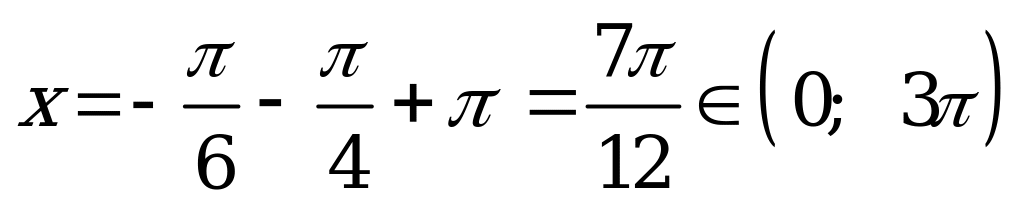 ;
;
при 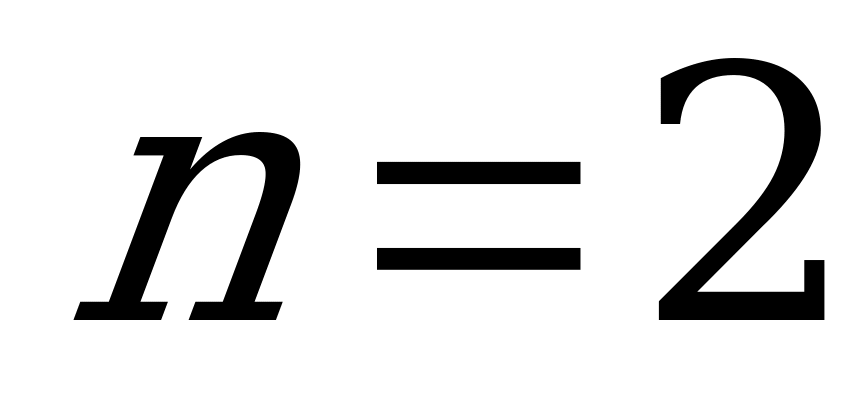
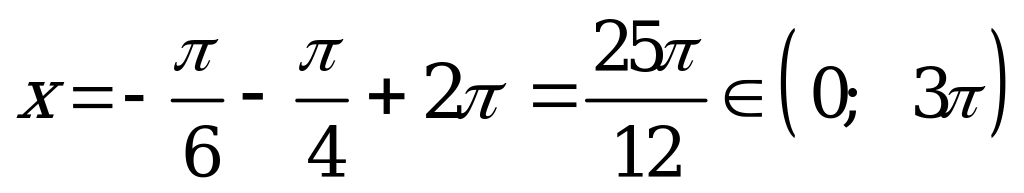 ;
;
при 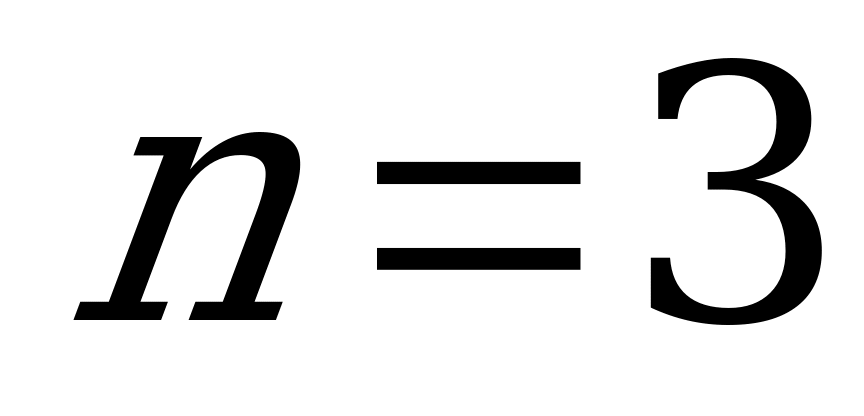
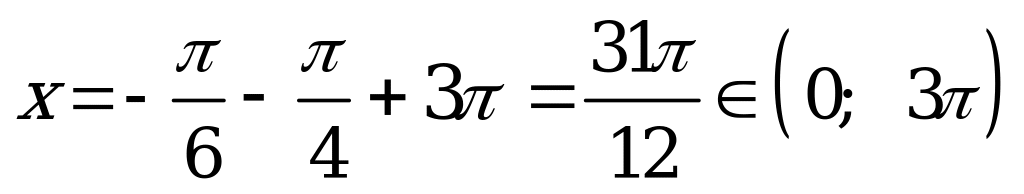 .
.
При 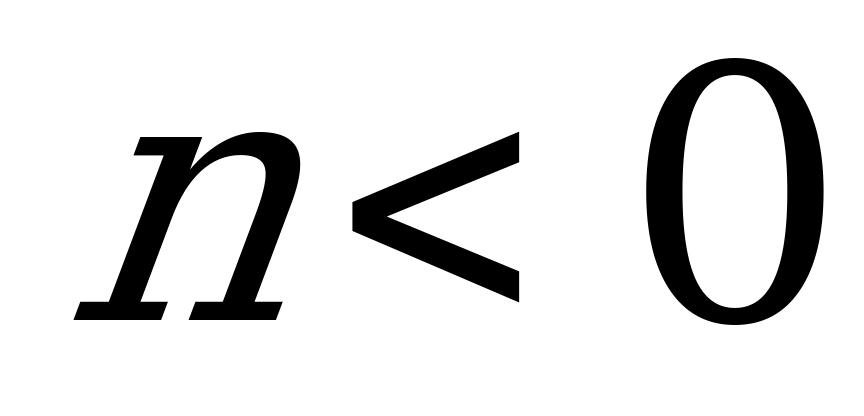 и
и 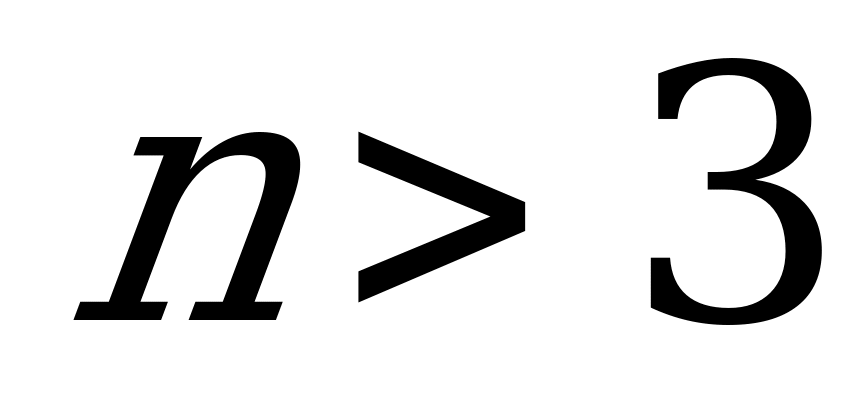 корни не принадлежат интервалу
корни не принадлежат интервалу 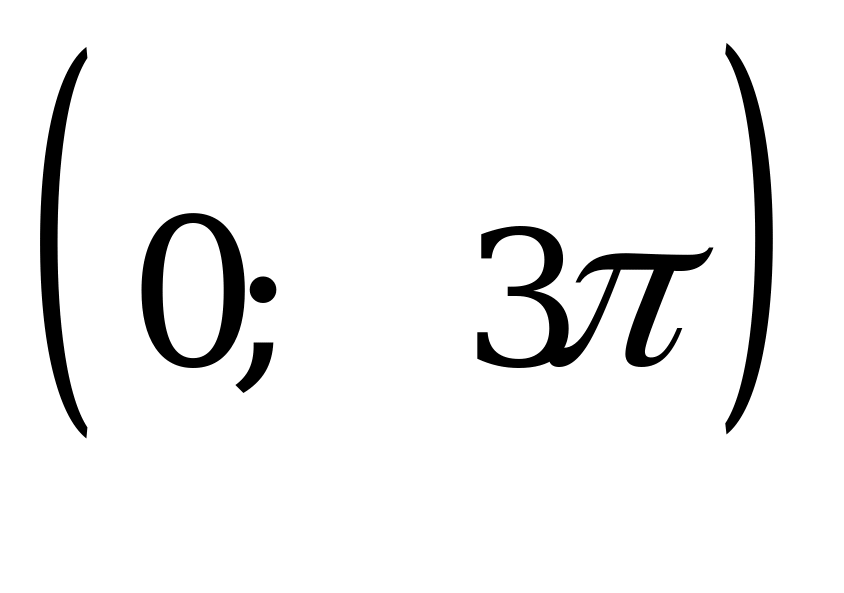 . Следовательно, число корней равно 4.
. Следовательно, число корней равно 4.
Ответ: 4.
Пример 2. Найти число корней уравнения 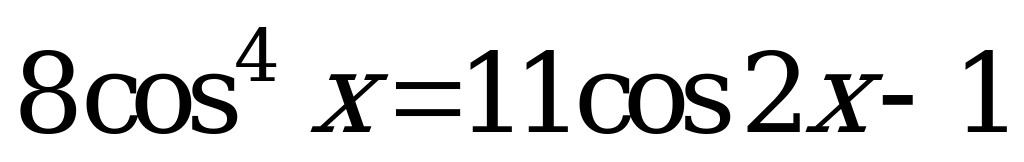 , принадлежащих интервалу
, принадлежащих интервалу 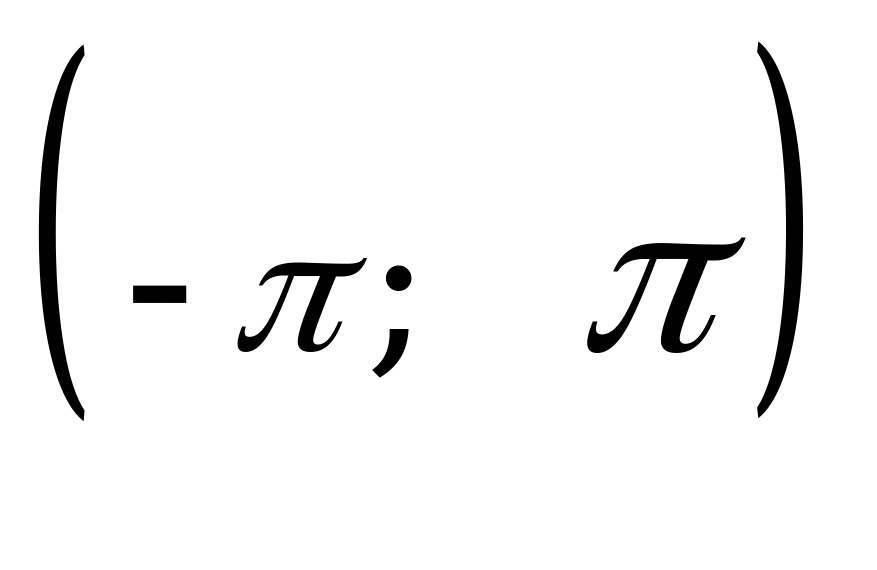 .
.
Решение. Преобразуем уравнение к виду 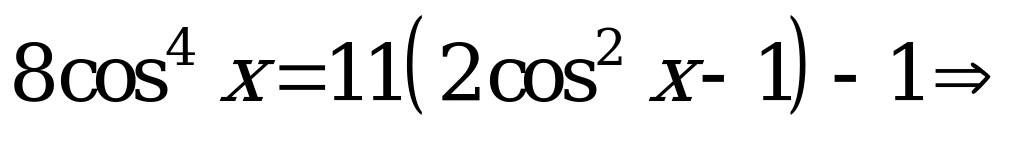
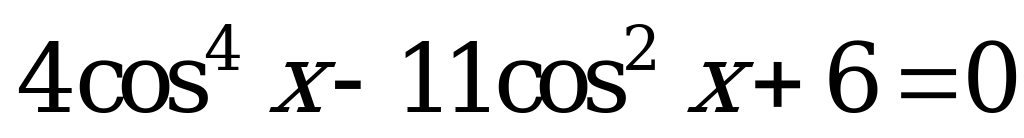 . Введем новую переменную
. Введем новую переменную 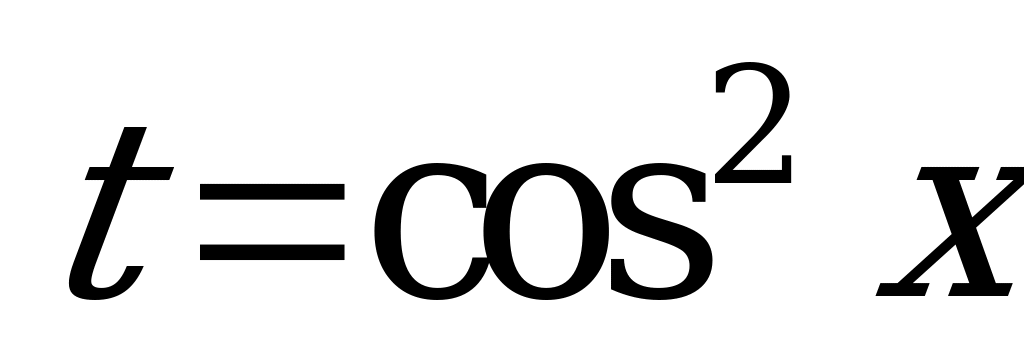 , где
, где 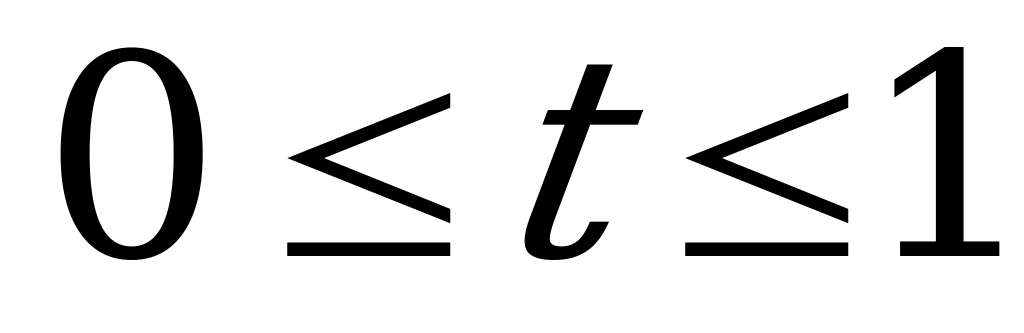 . Тогда получим квадратное уравнение
. Тогда получим квадратное уравнение 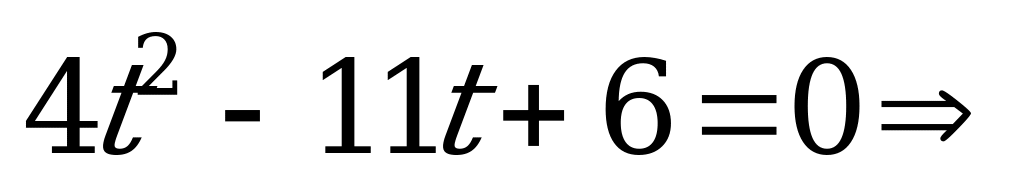
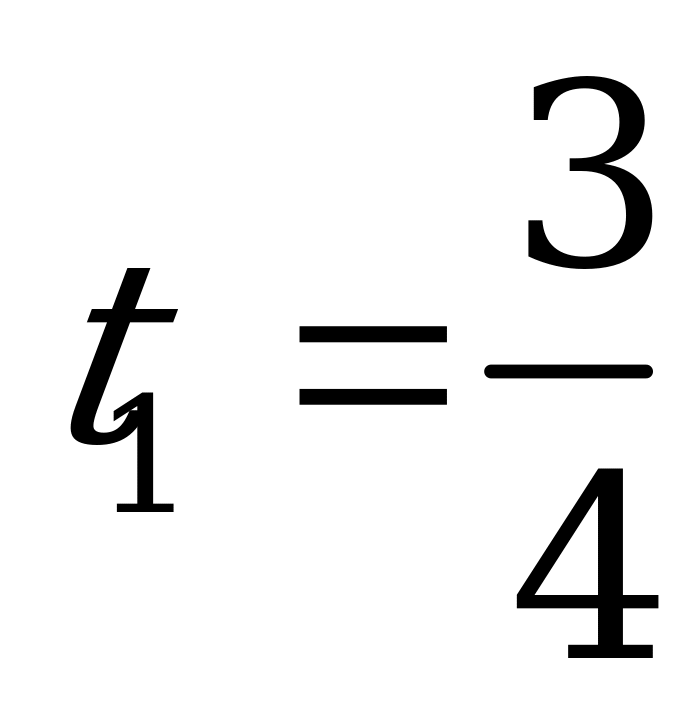 и
и 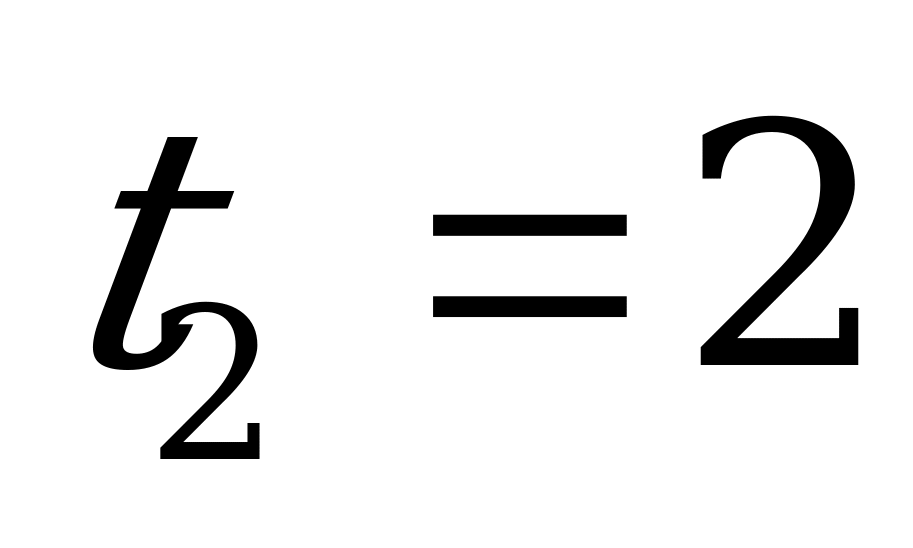 , где
, где  не подходит по смыслу замены. Следовательно, исходное уравнение равносильно совокупности уравнений
не подходит по смыслу замены. Следовательно, исходное уравнение равносильно совокупности уравнений 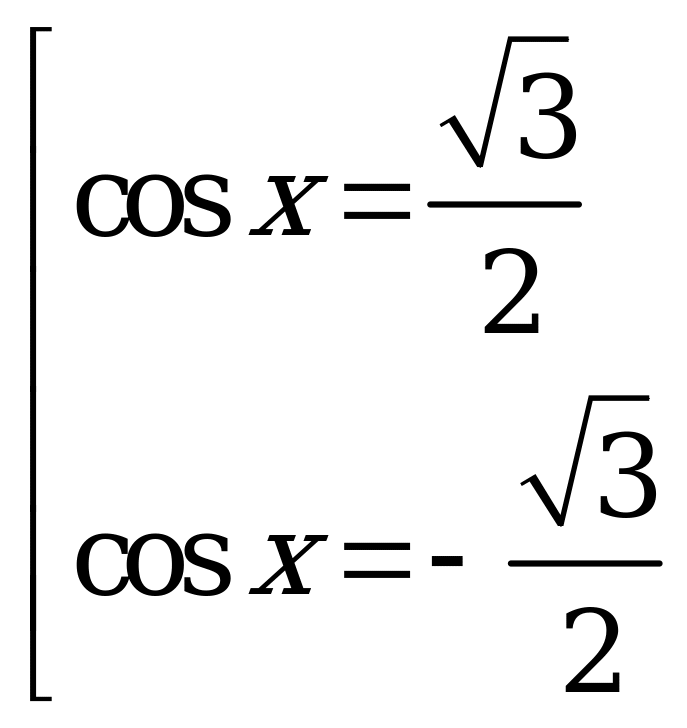 , решением которой является множество
, решением которой является множество  . Отбираем корни на интервале
. Отбираем корни на интервале 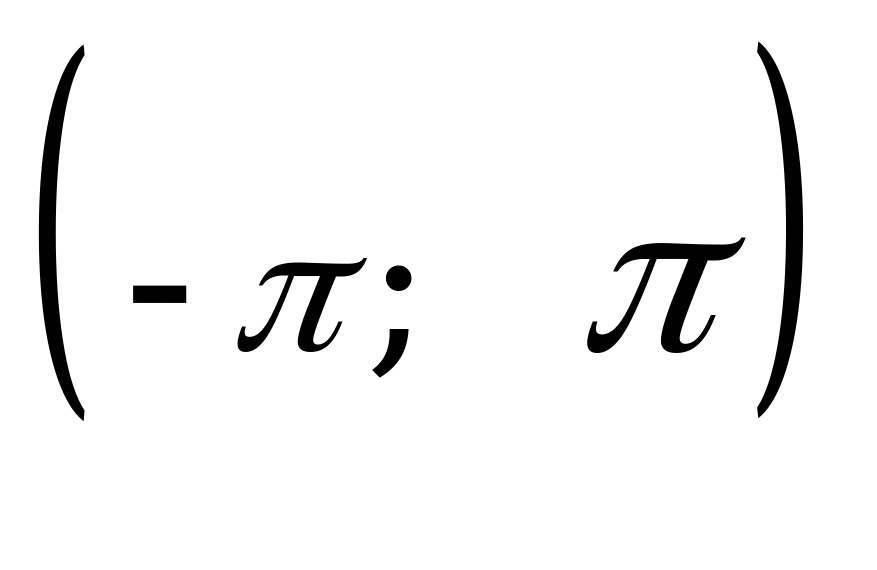 :
:
при 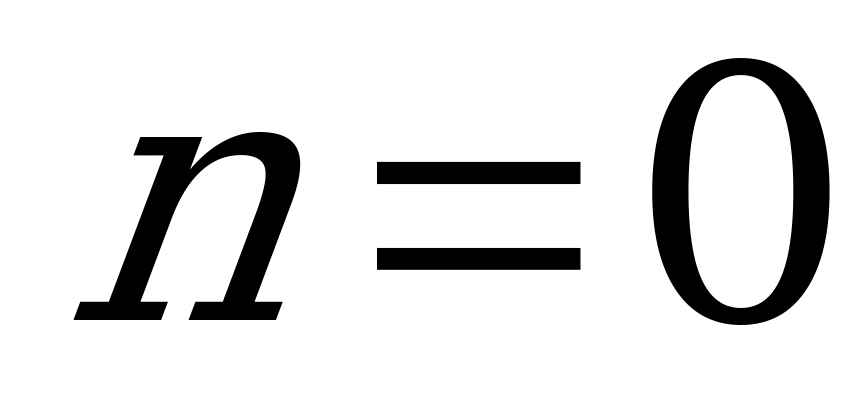
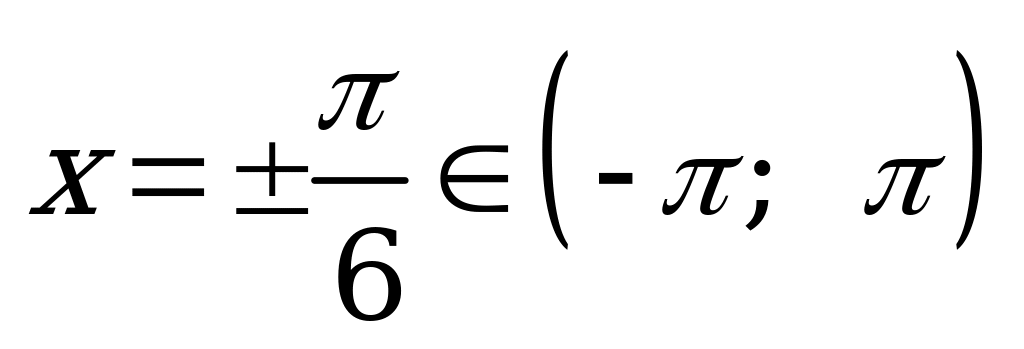 ; при
; при 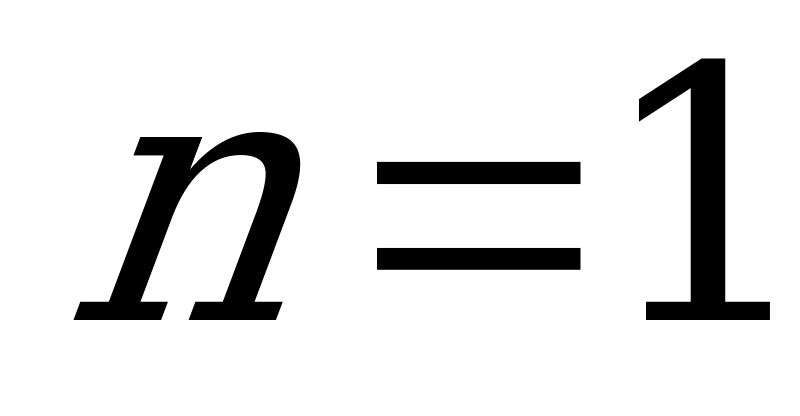
 ; при
; при 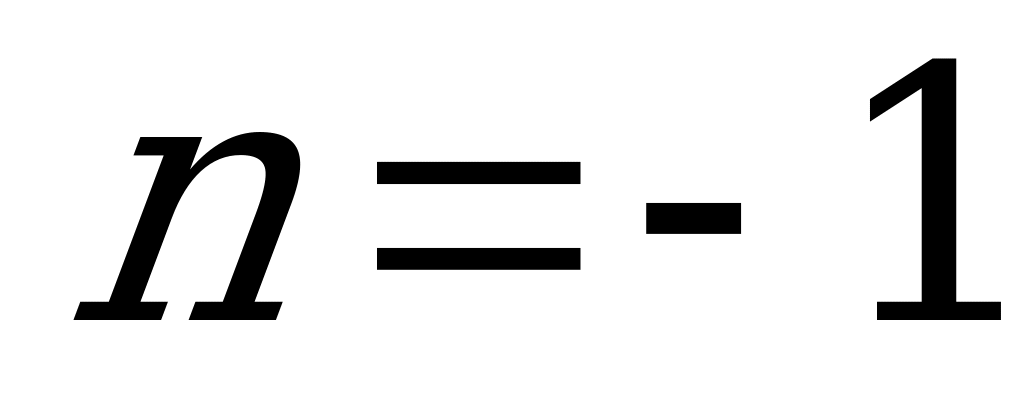
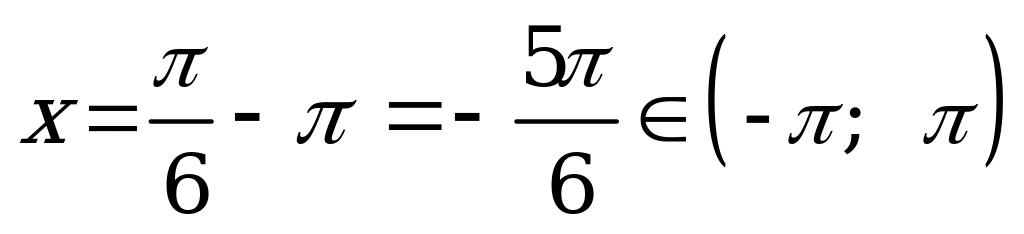 . Других корней на этом интервале нет. Следовательно, число корней равно 4.
. Других корней на этом интервале нет. Следовательно, число корней равно 4.
Ответ: 4.
Пример 3. Найти число корней уравнения 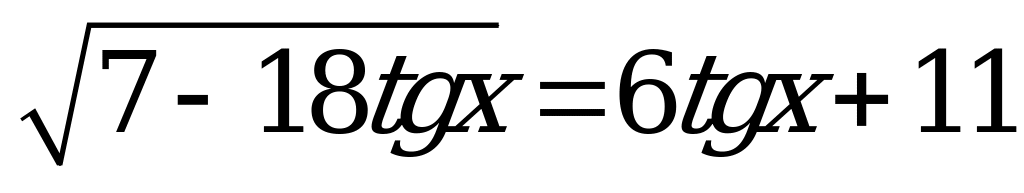 на интервале
на интервале 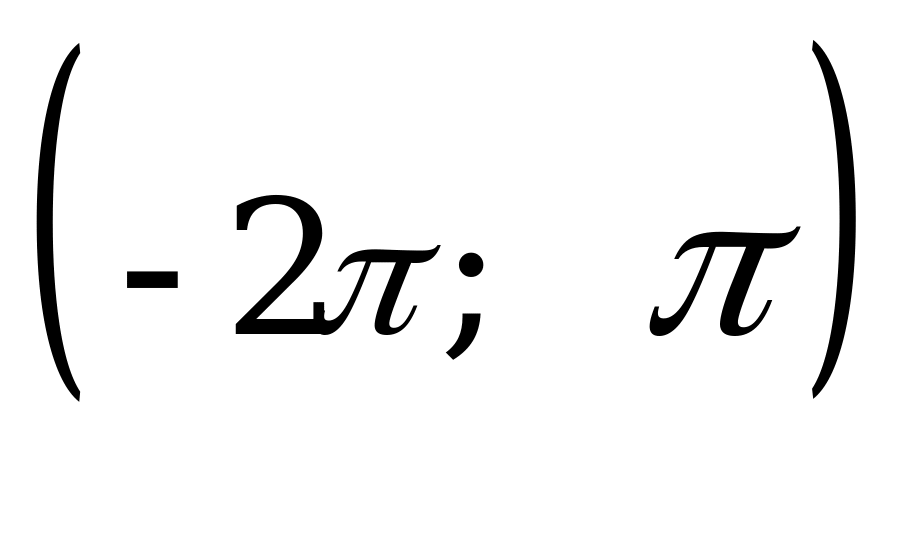 .
.
Решение. Введем новую переменную 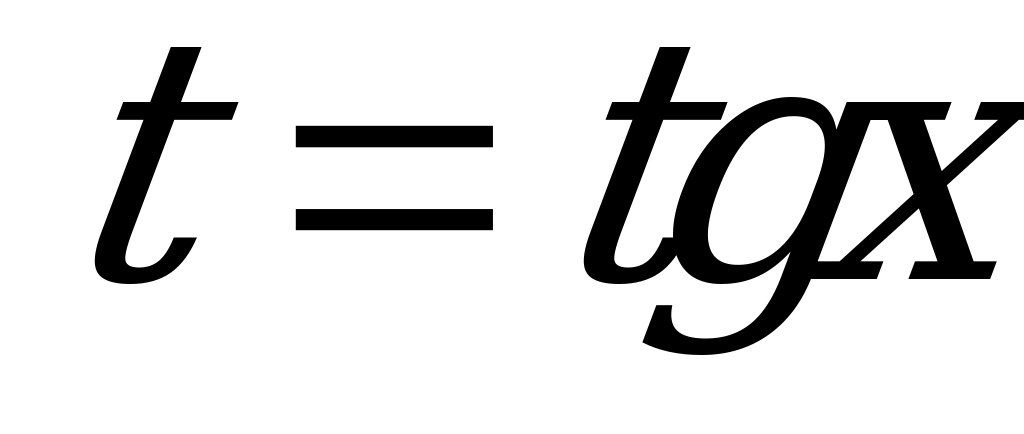 . Тогда получим иррациональное уравнение
. Тогда получим иррациональное уравнение 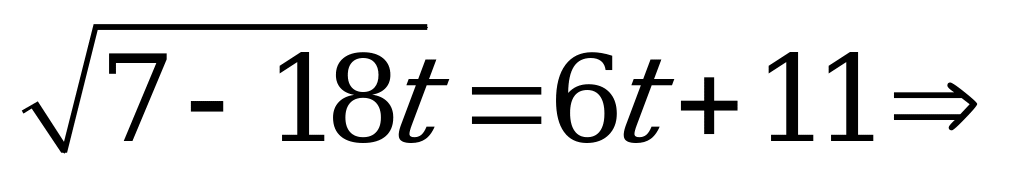
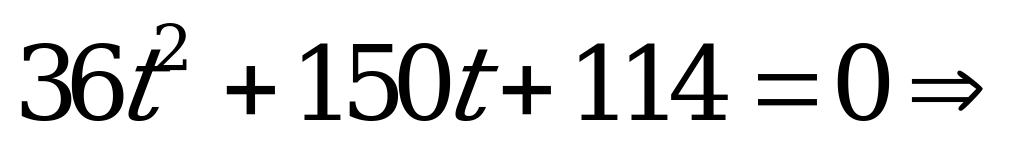
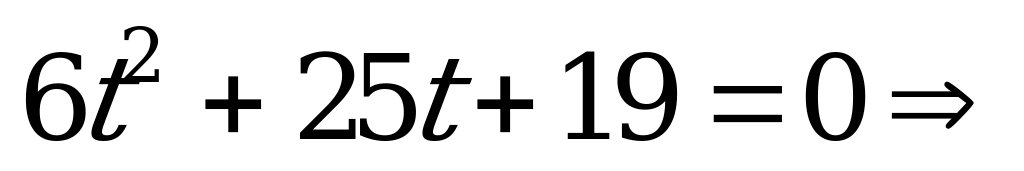
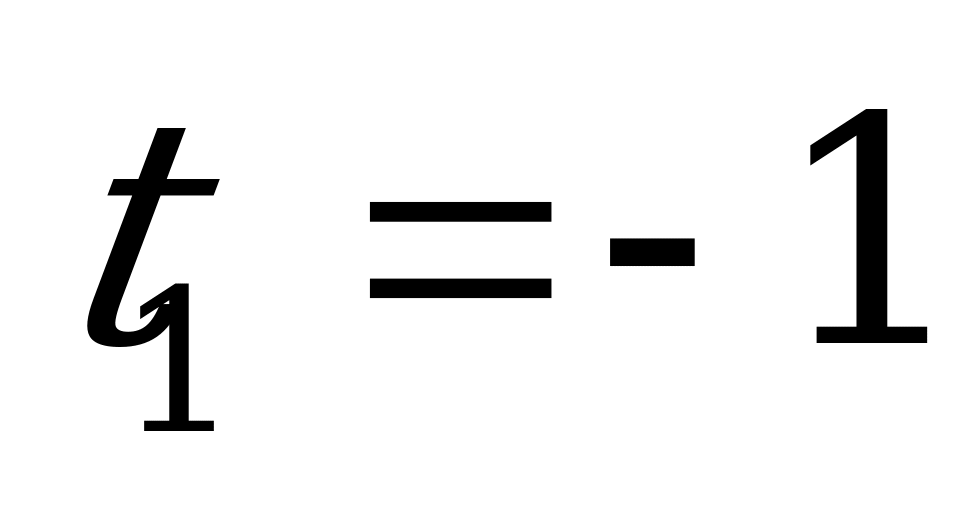 ,
, 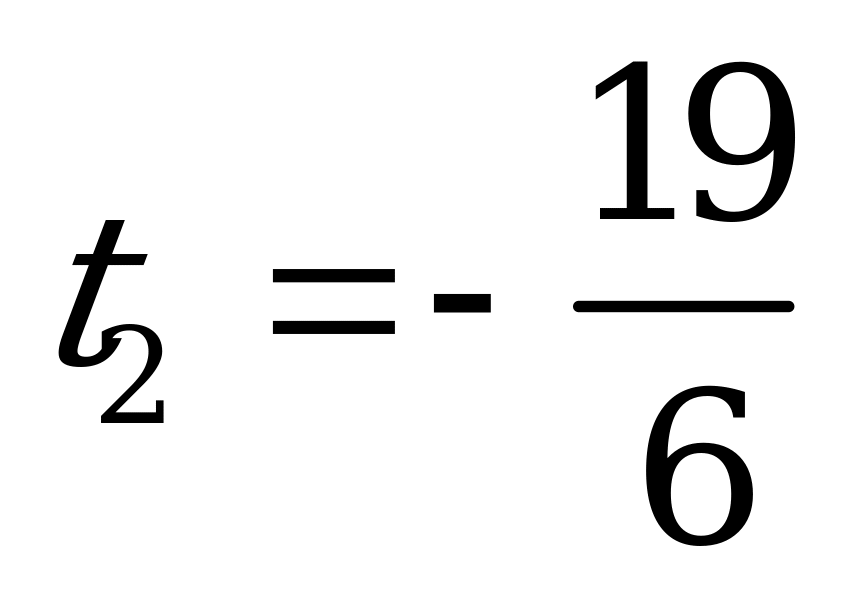 – посторонний корень. Следовательно,
– посторонний корень. Следовательно, 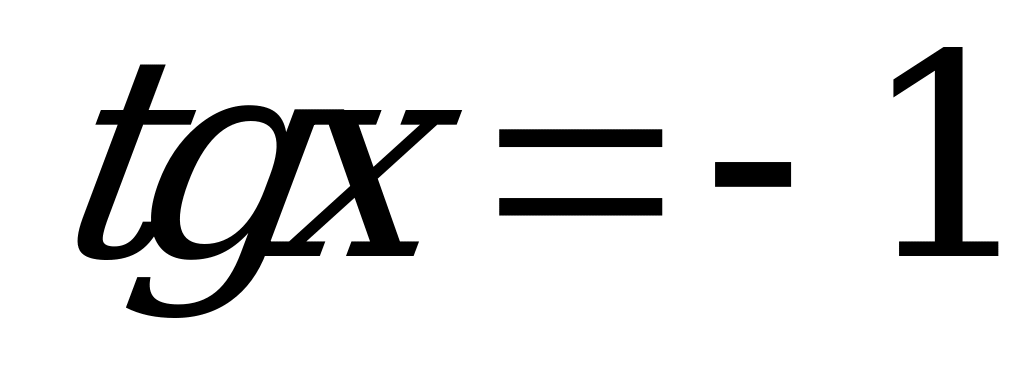 и
и 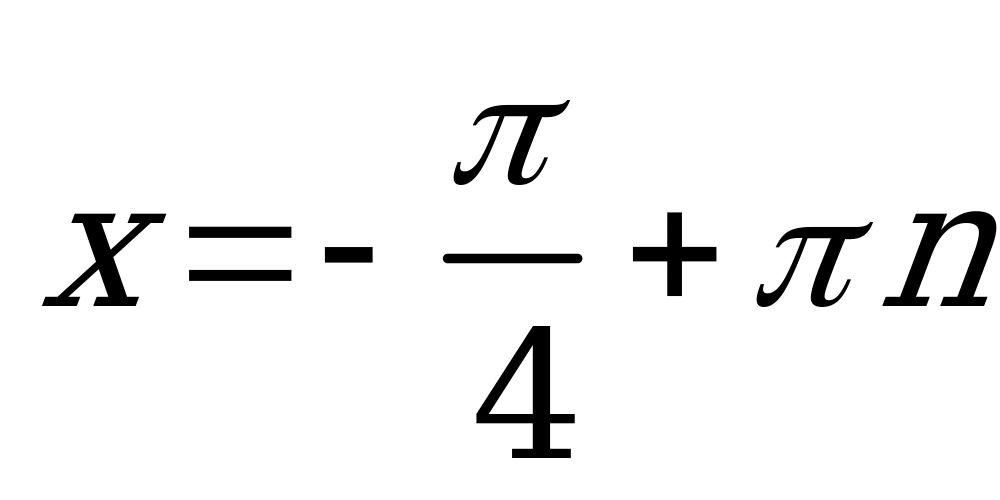 ,
,  . Отбираем корни на интервале
. Отбираем корни на интервале 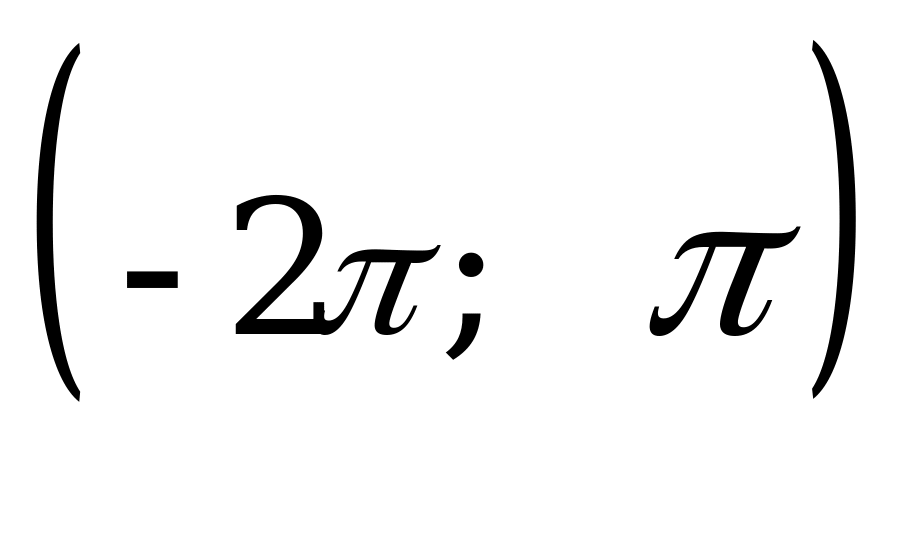 : при
: при 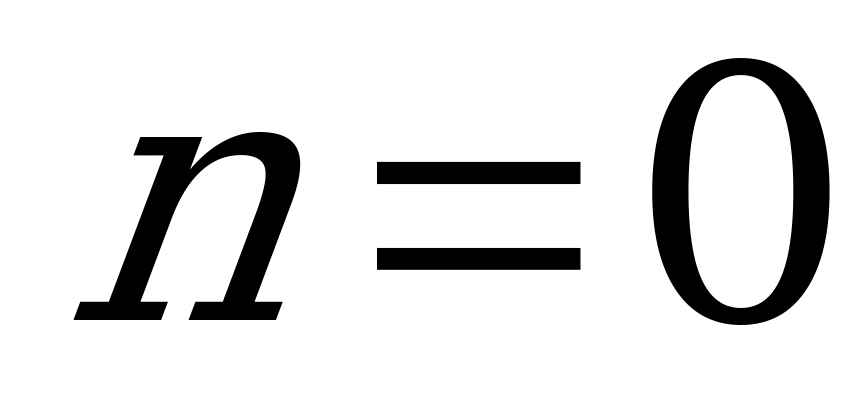
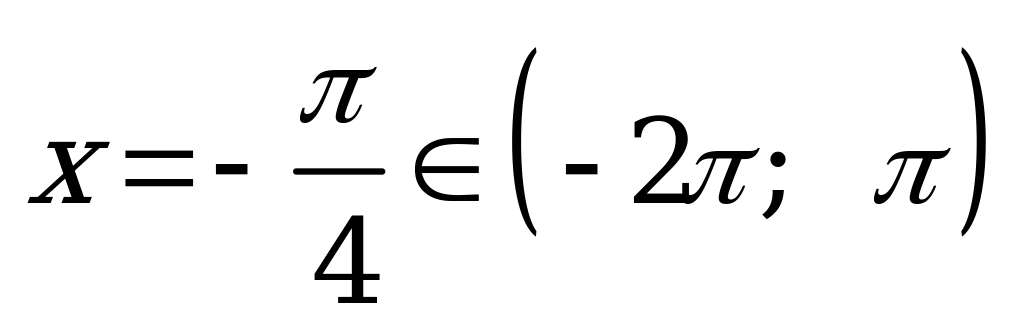 ; при
; при 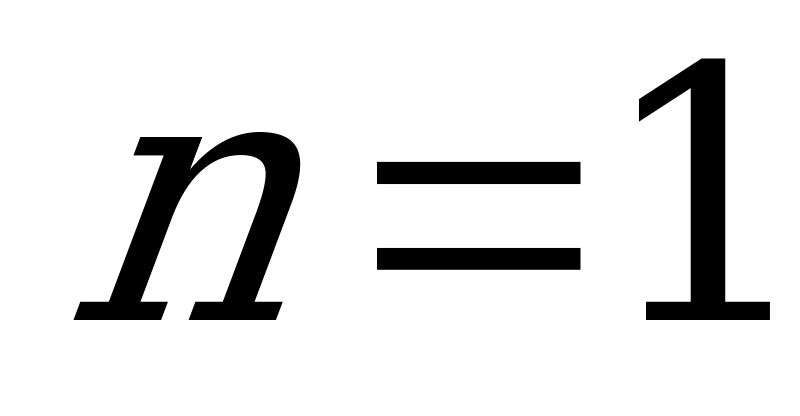
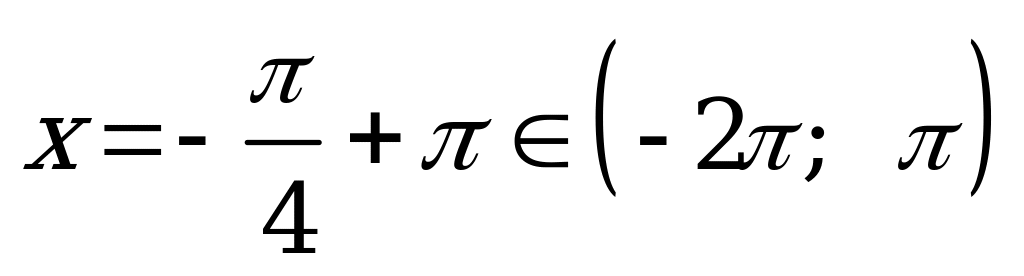 ; при
; при 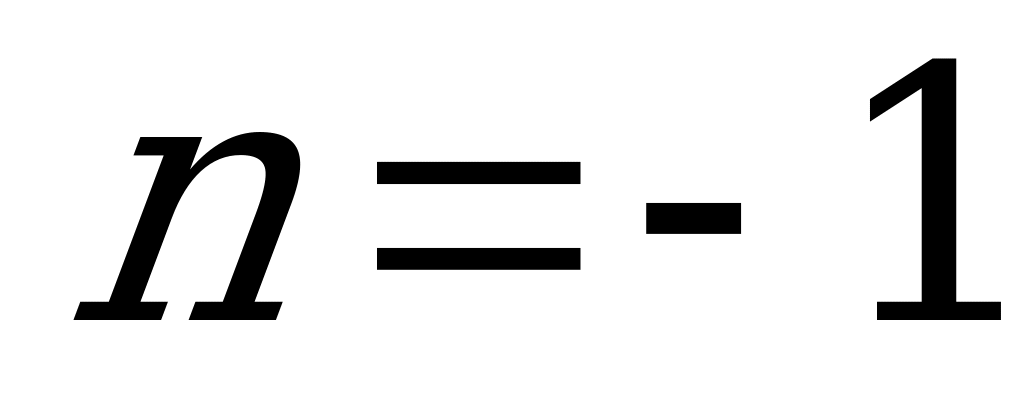
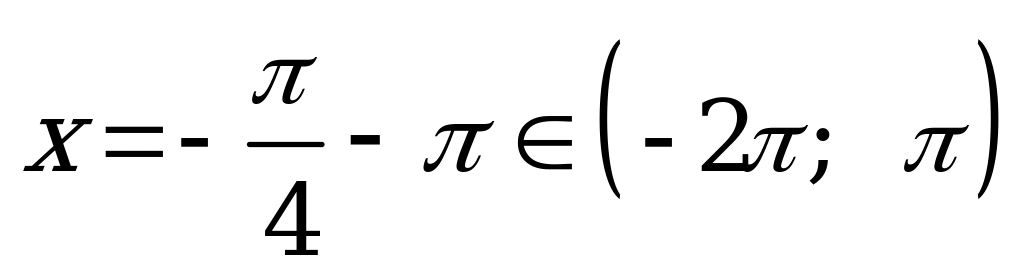 . Других корней на этом интервале нет. Следовательно, число корней равно 3.
. Других корней на этом интервале нет. Следовательно, число корней равно 3.
Ответ: 3.
Пример 4. Найти число корней уравнения 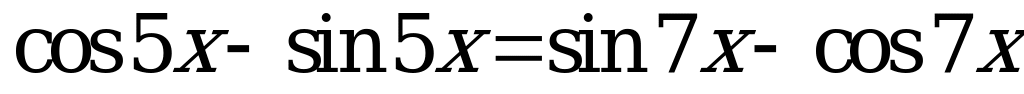 на интервале
на интервале 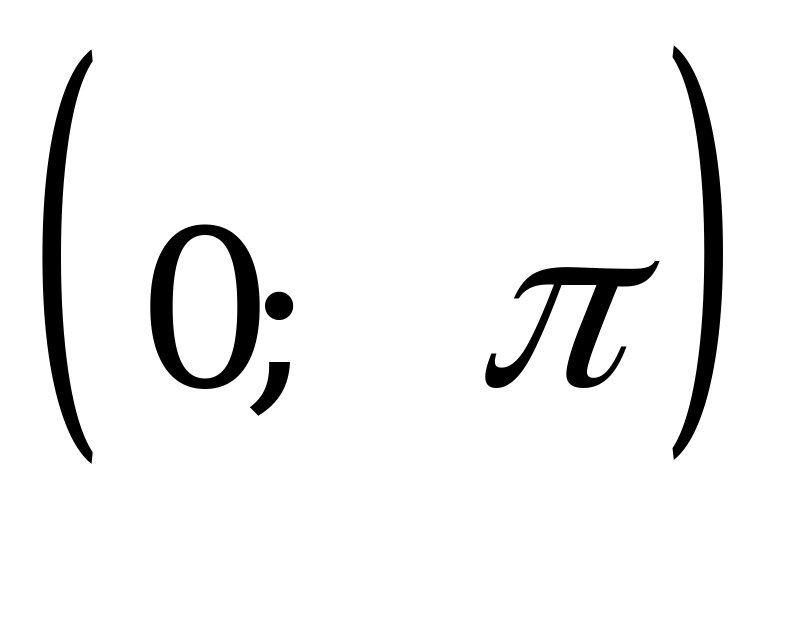 .
.
Решение. Группируя слагаемые, получим 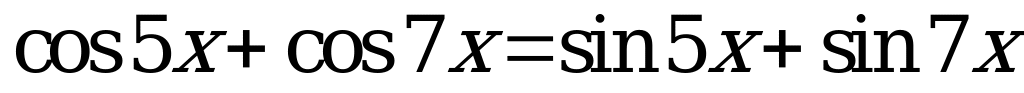 . Преобразуя суммы в произведения, приводим уравнение к виду
. Преобразуя суммы в произведения, приводим уравнение к виду 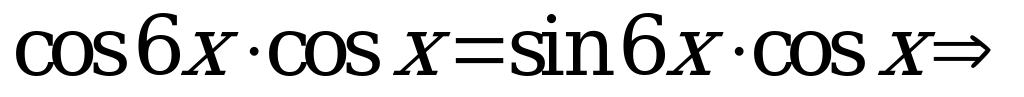
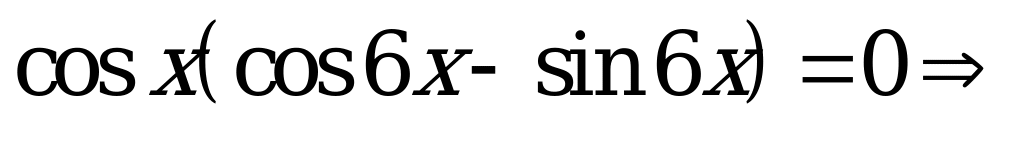
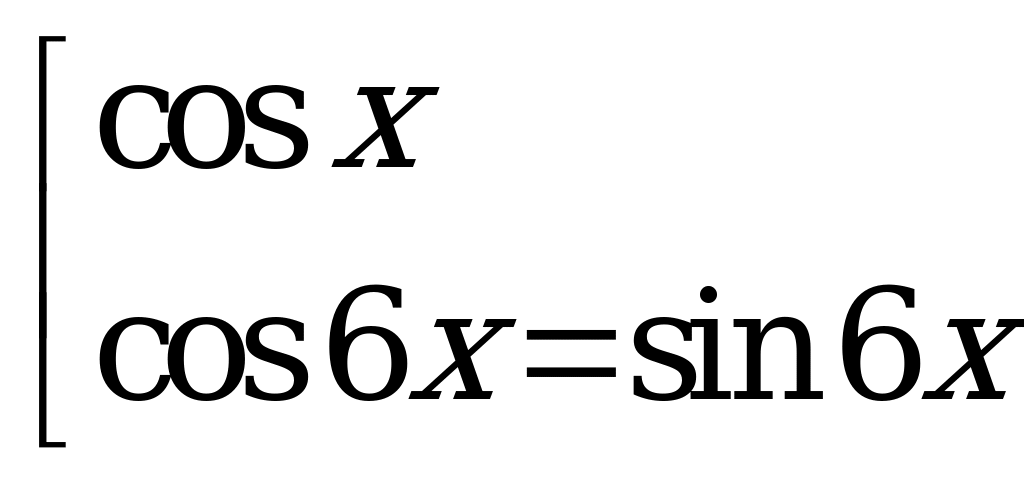 . Отсюда
. Отсюда 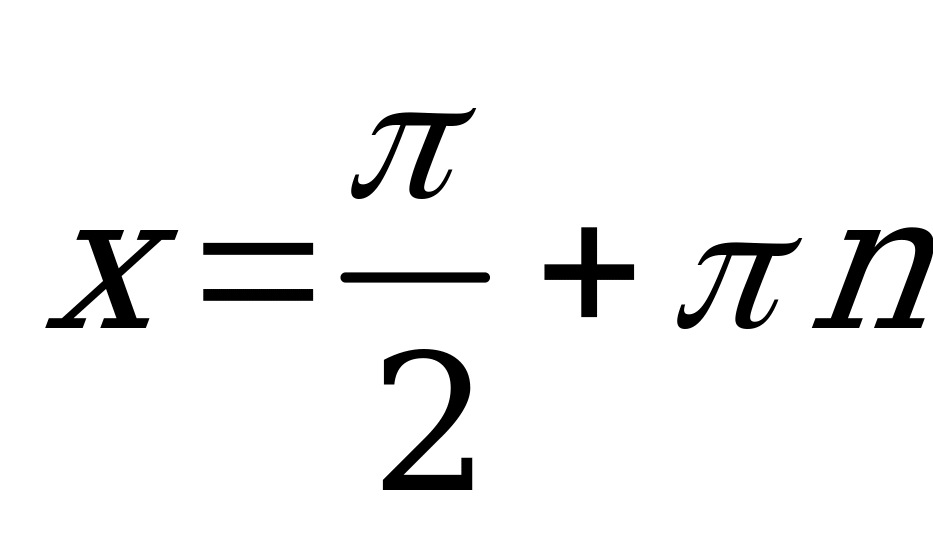 ,
,  и
и 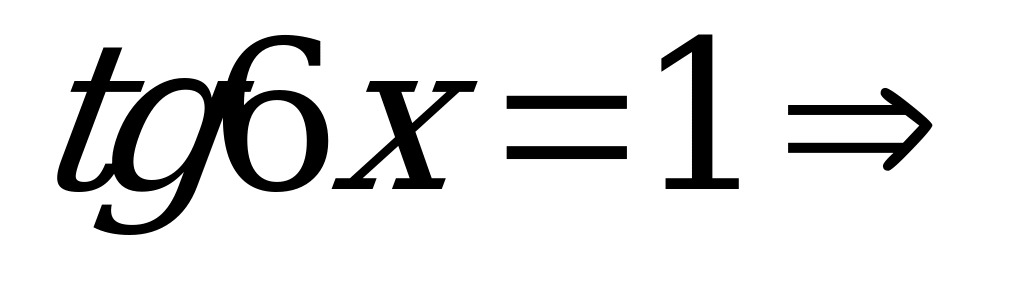
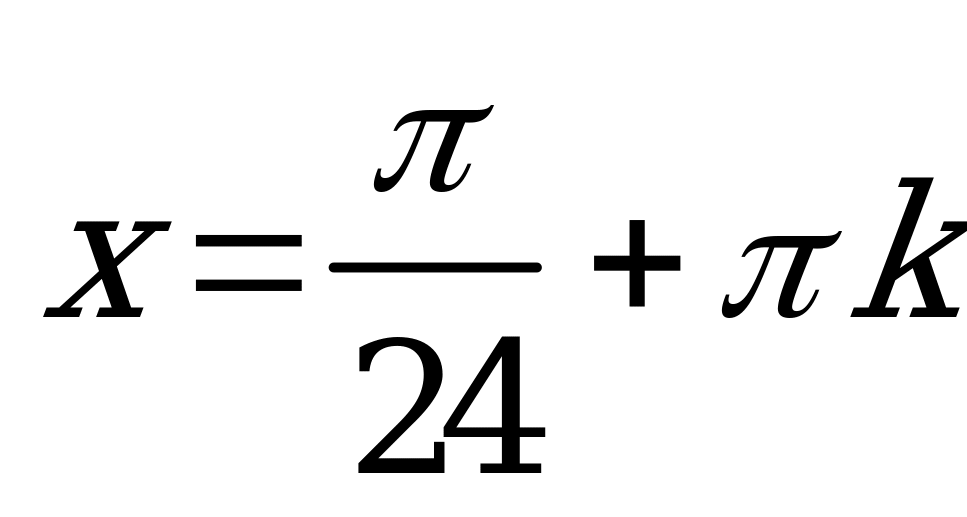 ,
, 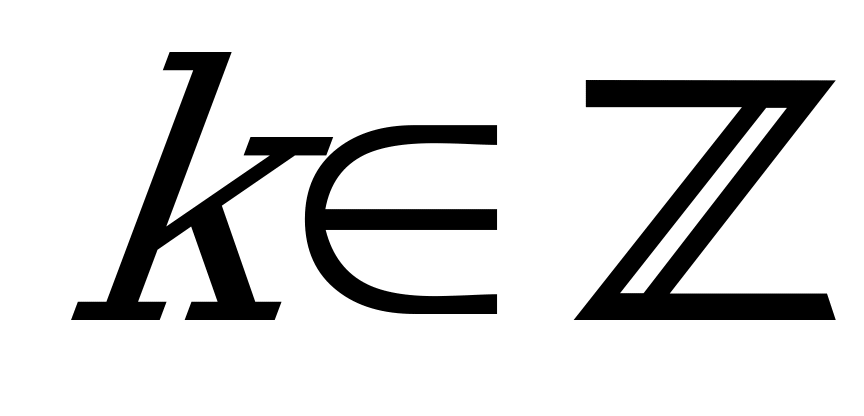 . Отбираем корни на интервале
. Отбираем корни на интервале 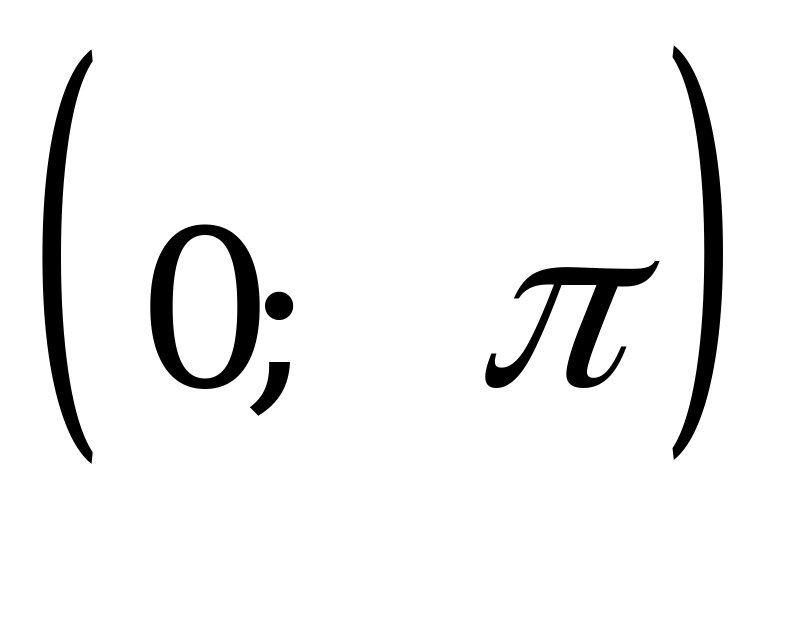 : при
: при 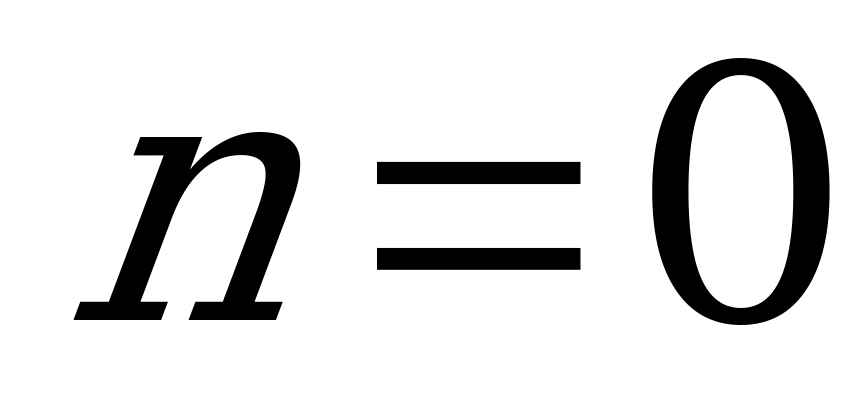
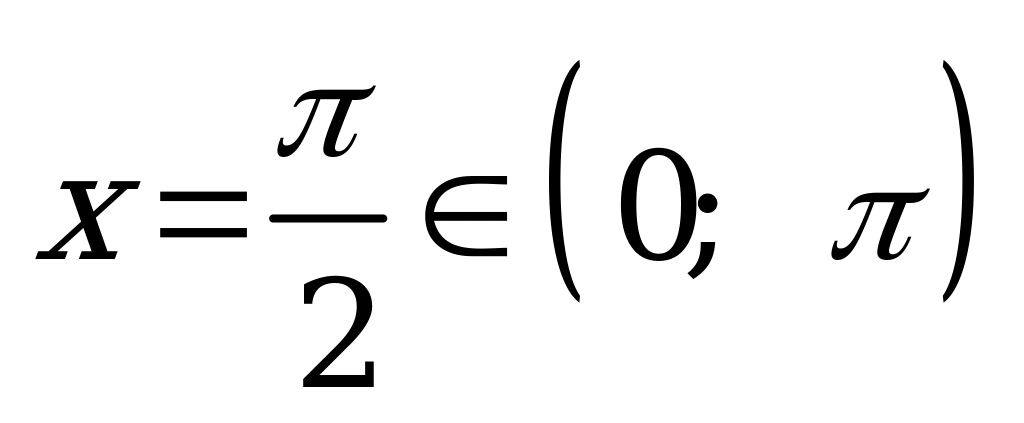 ; при
; при 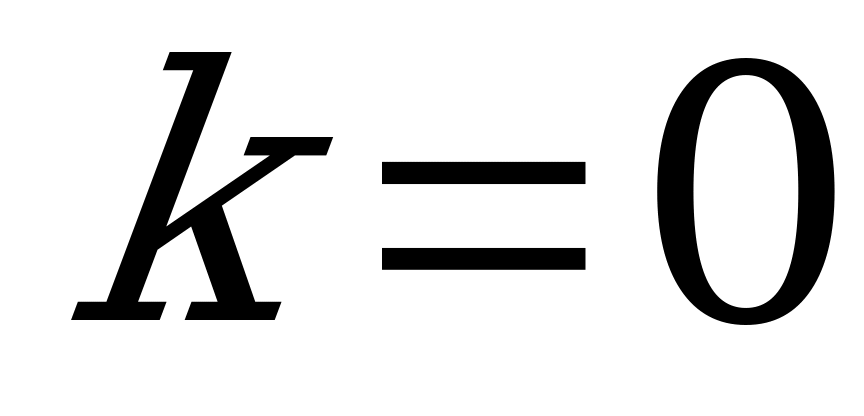
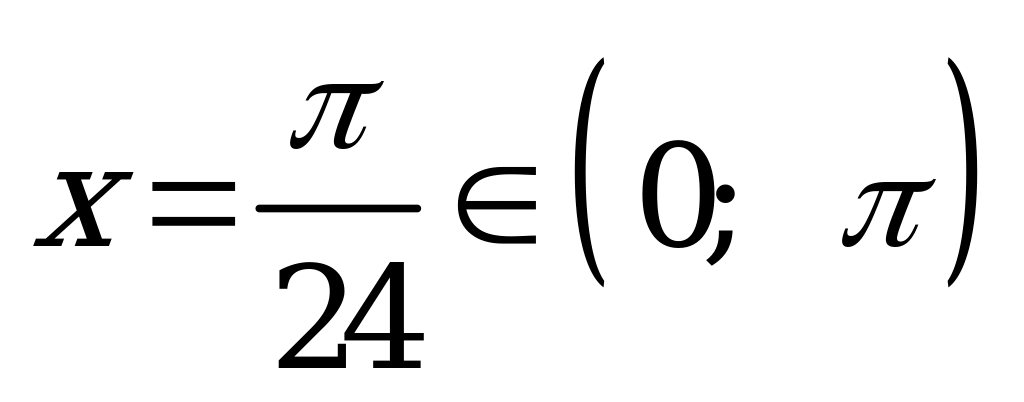 ; при
; при 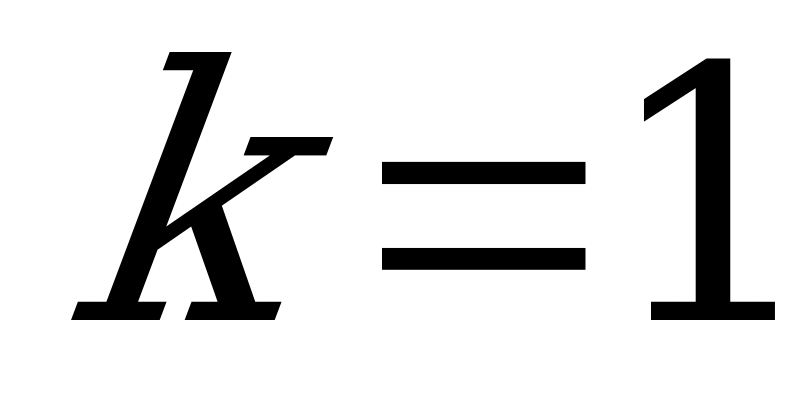
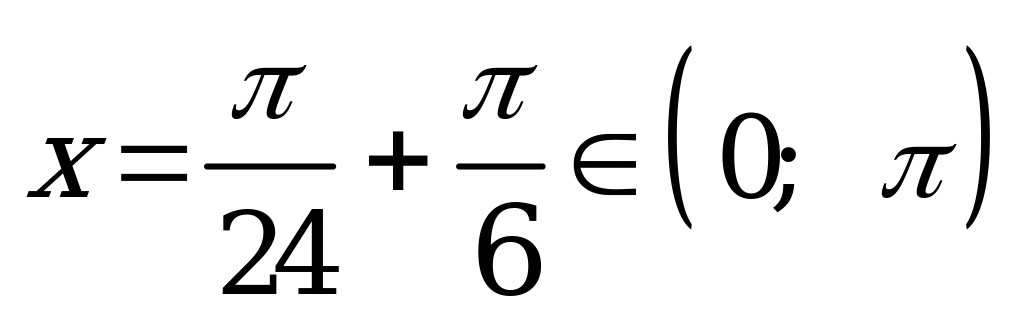 ; при
; при 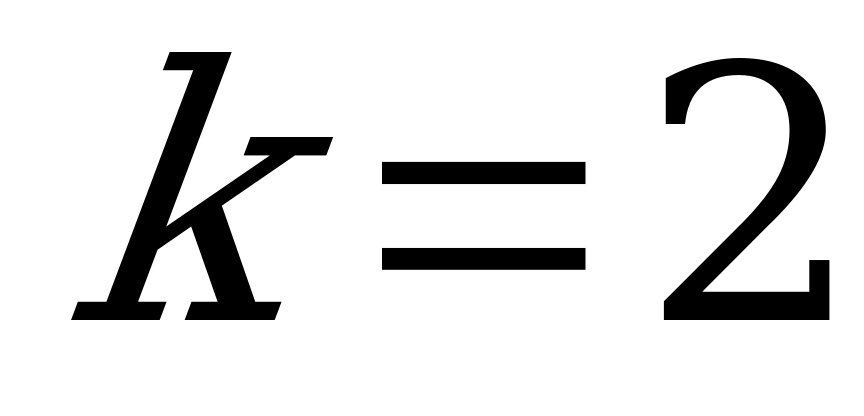
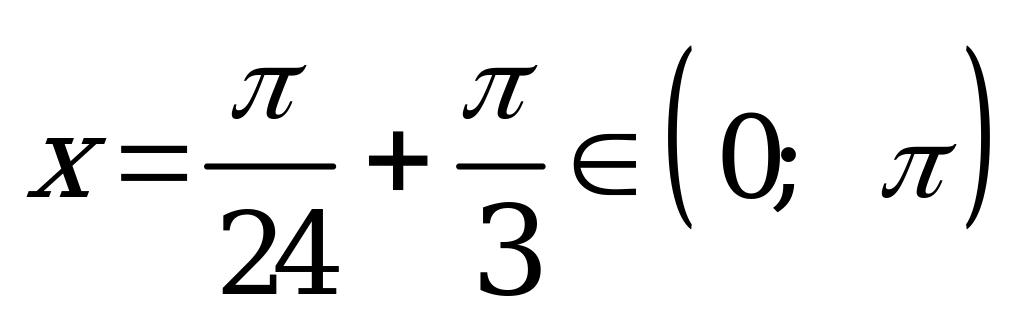 ; при
; при 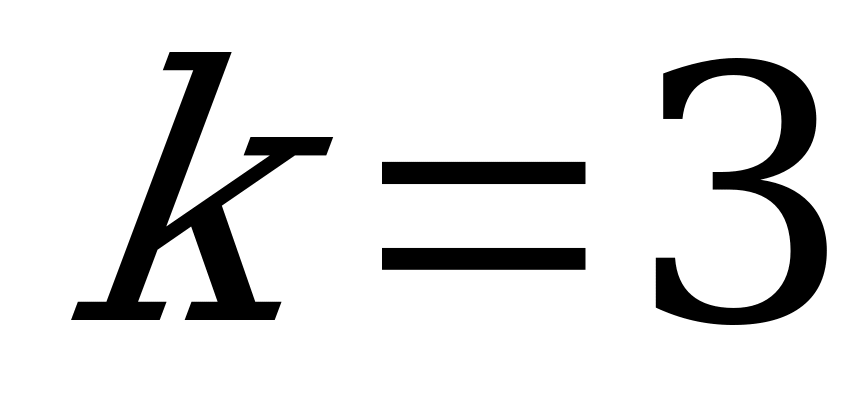
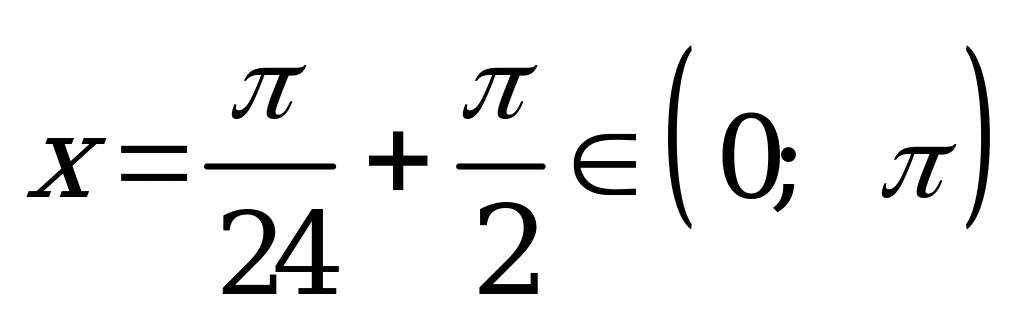 ; при
; при 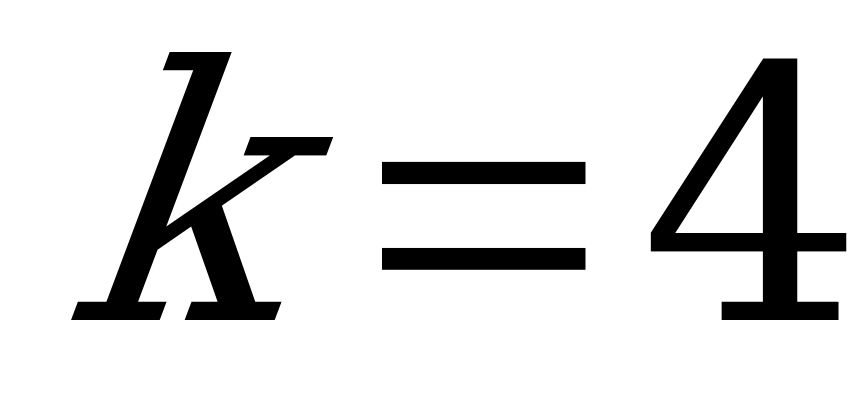
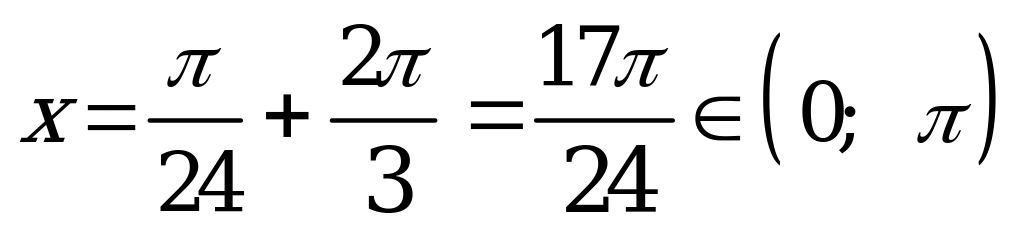 ; при
; при 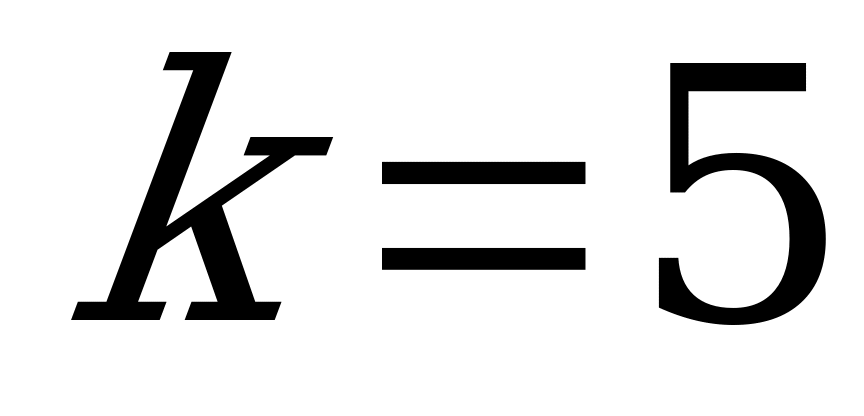
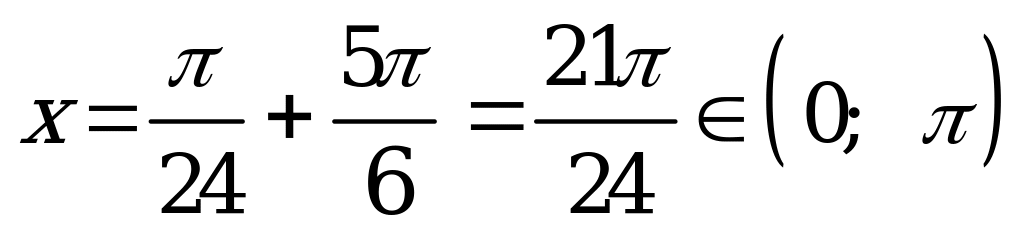 . Других корней на этом интервале нет. Следовательно, число корней равно 7.
. Других корней на этом интервале нет. Следовательно, число корней равно 7.
Ответ: 7.
Пример 5. Найдите в градусах среднее арифметическое всех различных корней уравнения 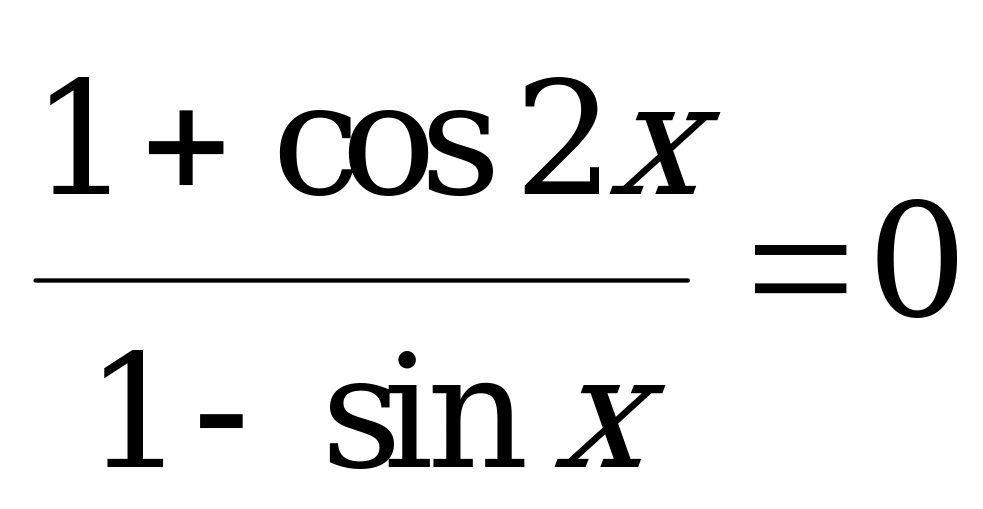 , принадлежащих промежутку
, принадлежащих промежутку 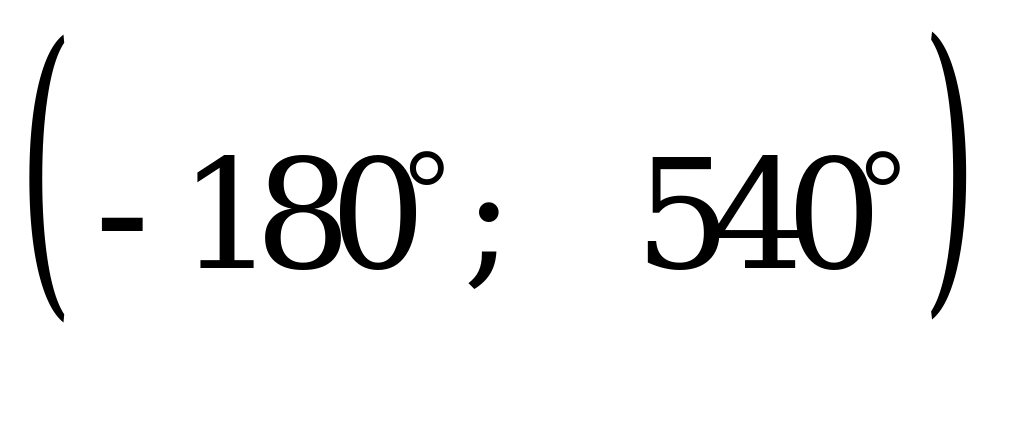 .
.
Решение. Данное уравнение равносильно системе 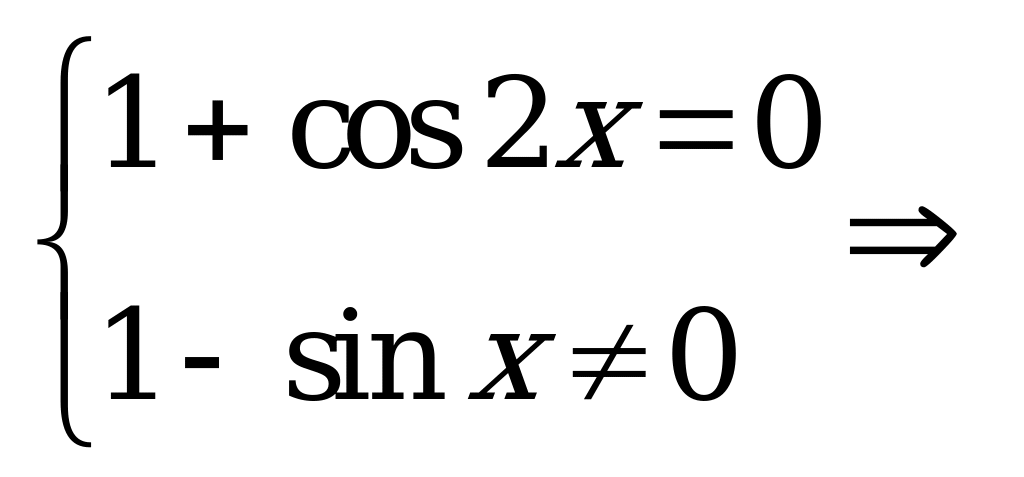
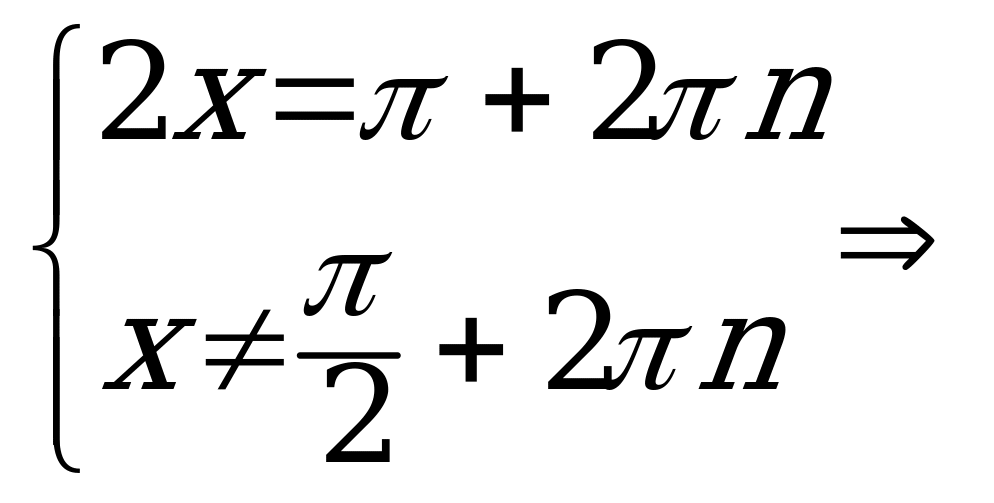
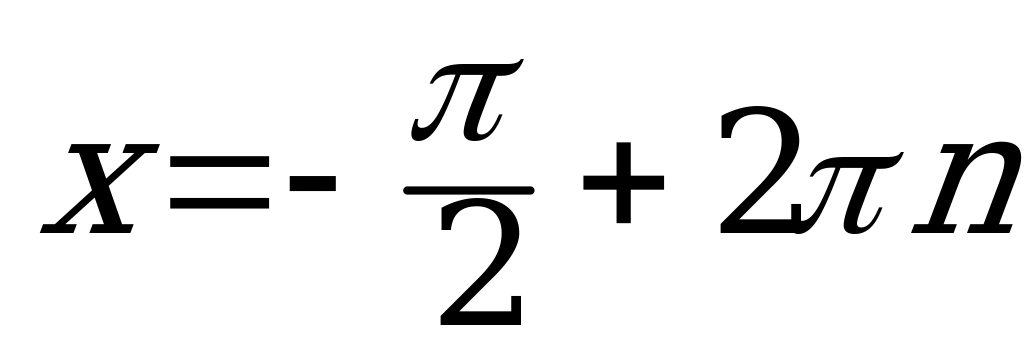 ,
,  .
.
Среди корней этого уравнения промежутку 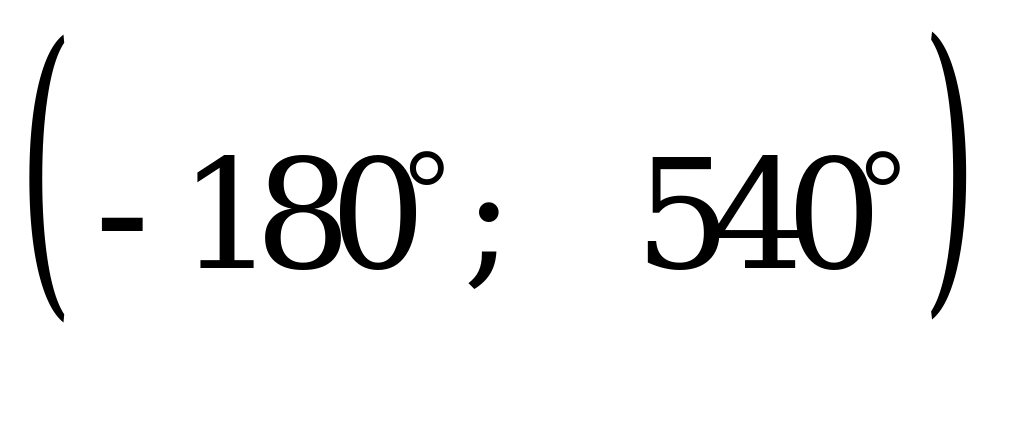 принадлежат
принадлежат  и
и  . Среднее арифметическое этих корней равно
. Среднее арифметическое этих корней равно  .
.
Ответ:  .
.
1.3 История понятия “тригонометрия”
Слово “тригонометрия” (от греческих слов “тригон” - треугольник и “метрео” - измеряю) означает “измерение треугольников”. Возникновение тригонометрии связано с развитием астрономии и географии.
Начала тригонометрии обнаружены в сохранившихся документах Древнего Вавилона, сведения тригонометрического характера встречаются и в старинных памятниках других народов древности.
Древнегреческие учёные впервые поставили перед собой задачу решения прямоугольного треугольника, т.е. определения его элементов по трём данным элементам, среди которых хотя бы один – сторона треугольника. Для решения этой задачи Гиппарх и Птолемей (II в. до н. э.) составили таблицы длин хорд, соответствующих различным центральным углам кругам постоянного радиуса (через каждые полградуса до 180°).
Понятия синуса, косинуса и тангенса угла возникли в астрономии и геометрии. По существу, ими оперировали ещё древние математики, рассматривая отношения отрезков в треугольниках и окружностях. Древнегреческий учёный Клавдий Птолемей для своих астрономических исследований составил подробную, весьма точную таблицу синусов углов, в течение многих веков служившую средством для решения треугольников.
В XI-XIII вв. в трудах математиков Средней Азии, Закавказья, Ближнего Востока и Индии началось формирование тригонометрии как отдельной науки. У индийских учёных линия синусов именовалась “архаджива”, что буквально означало “половина тетивы лука”. Для угла a линия синусов – это хорда единичной окружности, соответствующая центральному углу 2а. Её длина равна 2 sina. В Индии были составлены таблицы значений синусов для всех углов от 0 до 90° через каждые 3°45'. Эти таблицы были точнее таблиц Птолемея. Об их высокой точности говорит тот факт, что для синуса и косинуса 3°45' были вычислены значения 100/1529 и 466/467, отличающиеся от истинный менее чем на 0,00000001.
Косинус индийцы называли “котиджива”, т.е. синус остатка (до четвери окружности). В XV в. немецкий учёный Иоганн Мюллер (1436 - 1476), известный в науке под именем Региомонтам, как и другие математики, применял для понятия “косинус дуги x” латинский термин sinus complementi, т.е. синус дополнения, имея в виду sin(90° - x). От перестановки этих слов и сокращения одного из них (co-sinus) образовался термин “косинус”, встречающийся в 1620 г. у английского астронома Э. Гунтера, изобретателя счётной линейкой.
В IX-X вв. учёные стран Средней Азии (ал-Хабаш, ал-Баттани, Абу-л-Вефа и др.) ввели новые тригонометрические величины: тангенс и котангенс, секанс и косеканс. Понятия “тангенс” и “котангенс”, как и первые таблицы этих новых тригонометрических величин, родились не из рассмотрения тригонометрической окружности, а из учения о солнечный часах. Происхождение названия функции тангенс (термин введён в 1583 г. Немецким математиком Т. Финком), связана с геометрическим его представлением в виде отрезка прямой. Латинское слово tangens означает косающийся (отрезок касательной). Термин “котангенс” был образован в средние века по аналогии с термином “косинус”. Все три термина вырабатывались на протяжении веков и вышли во всеобщее употребление в первой половине XVII в.
В дальнейшем потребности географии, геодезии, военного дела способствовали развитию тригонометрии. Особенно усиленно шло её развитие в средневековое время, в первую очередь на юго-востоке: в Индии (Ариабхата, Брамагупта, Бхаскара), в Узбекистане, Азербайджане и Таджикистане (Насир ад-Дин ат-Тусси, ал-Каши, ал-Бируни), в Арибии (Ахмад Ибн-Абдаллах, ал-Баттани), а затем и в Европе (Пейрбах, Иоганн Мюллер, Коперник, Рети). Большая заслуга в формировании тригонометрии как отдельной науки принадлежит азербайджанскому учёному Насир ад-Дину ат-Туси (1201-1274), написавшему “Трактат о полном четырёхстороннике”.
Творения учёных этого периода привели к выделению тригонометрии как нового самостоятельного раздела науки. Однако в их трудах ещё не была введена необходимая символика, и поэтому развитие тригонометрии происходило очень медленно.
Современный вид тригонометрии получила в трудах Леонарда Эйлера (1707-1783). Он, в частности, вывел все тригонометрические формулы из нескольких основных, установил несколько неизвестных для него формул, ввёл единообразные знаки. Впервые в его трудах встречается запись sinx и др., доступно изложен вопрос о знаках тригонометрических функций в каждом квадрате, установлены формулы приведения.
Уже во “Введении в анализ бесконечных” (1748) Л. Эйлер впервые трактует синус, косинус и т.д. не как тригонометрические линии, обязательно связанные с окружностью, а как тригонометрические функции, которые он рассматривал как числовые величины.
До Эйлера совсем редко рассматривались тригонометрические функции дуг, превышающие π. Лишь в его трудах разрабатывается учение о тригонометрических функциях любого аргумента. На основании трудов Л. Эйлера были составлены учебники тригонометрии, излагавшие её в строгой научной последовательности.
Глава 2. Практикум по теме
«Решение тригонометрических уравнений».
Материал проекта представлен в виде практических заданий, которые позволят систематизировать и качественно улучшить уровень решения тригонометрических уравнений. В работе содержится достаточно большое количество взятых из различных источников заданий и упражнений, которые структурированы по методам решения уравнений - от самых элементарных до достаточно сложных.
Сводить тригонометрические уравнения к простейшим – задача творческая, тут нужно использовать и тригонометрические формулы, и особые методы решений уравнений:
- Метод введения новой переменной (самый популярный в ЕГЭ).
- Метод разложения на множители.
- Метод вспомогательных аргументов.
2.1 Самостоятельные работы № 1, № 2
Самостоятельная работа № 1 по теме
«Тригонометрические уравнения»
Вариант № 1 Решите уравнения:
1. 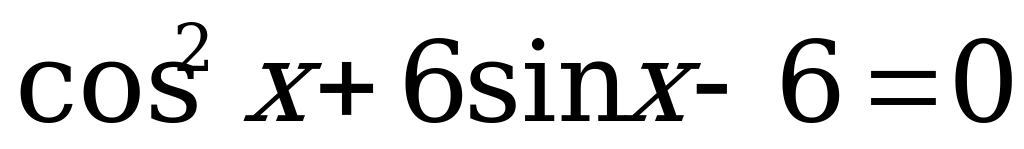
2. 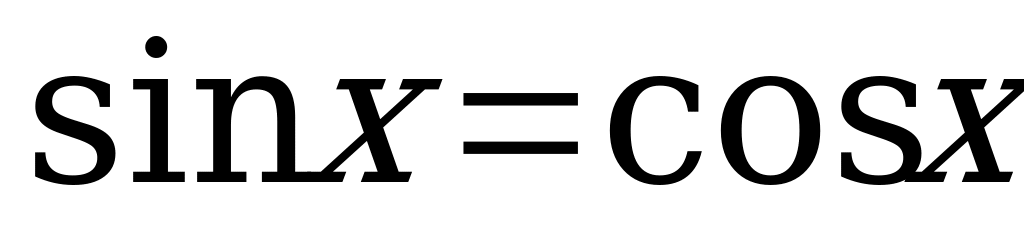
3. 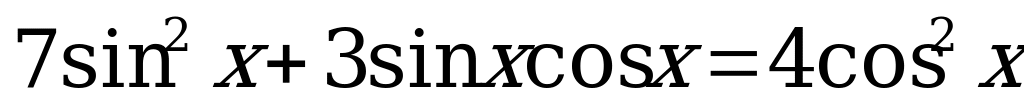
4. 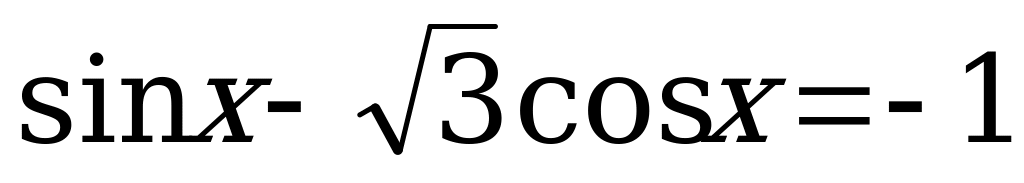
5. 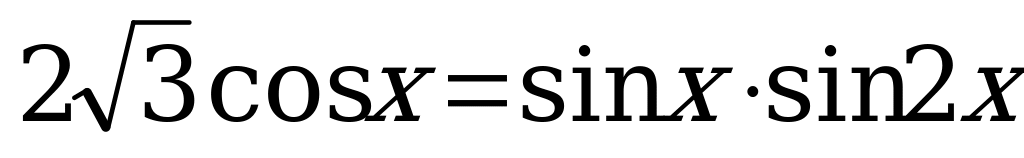
6. 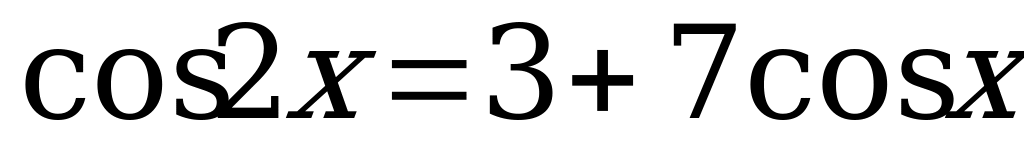
7. 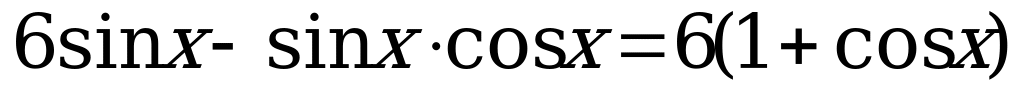
8. 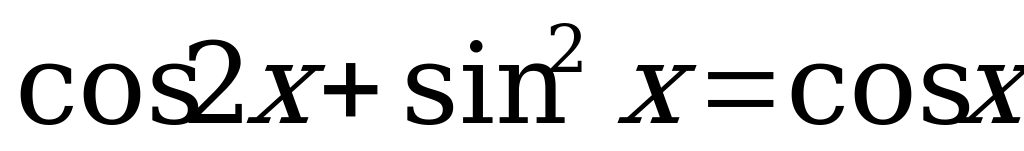 и найдите все его корни, принадлежащие промежутку
и найдите все его корни, принадлежащие промежутку 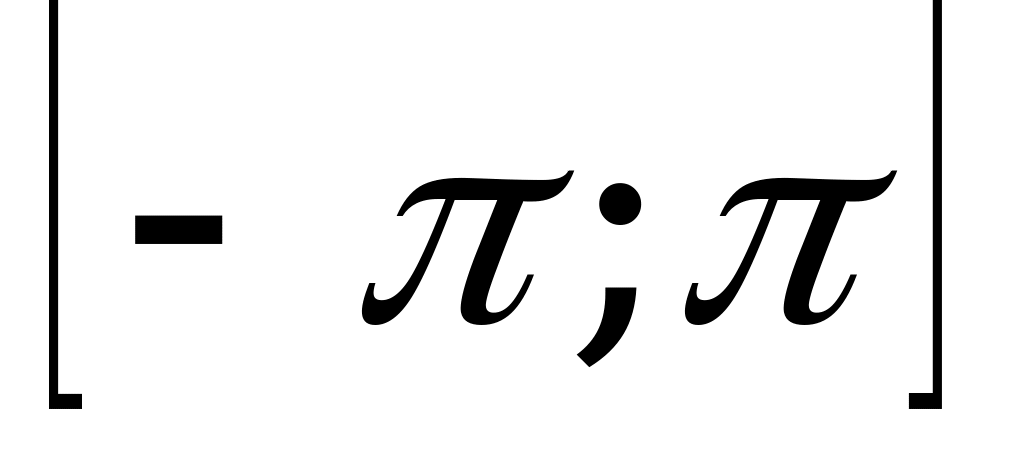 .
.
Вариант № 2 Решите уравнения:
1. 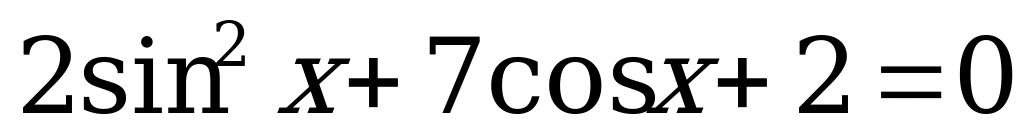
2. 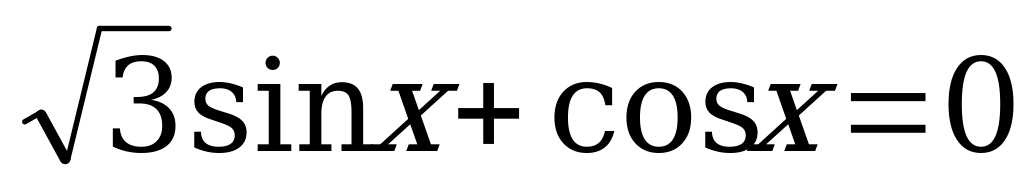
3. 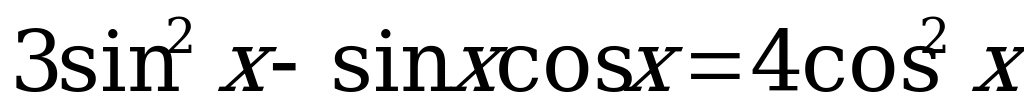
4. 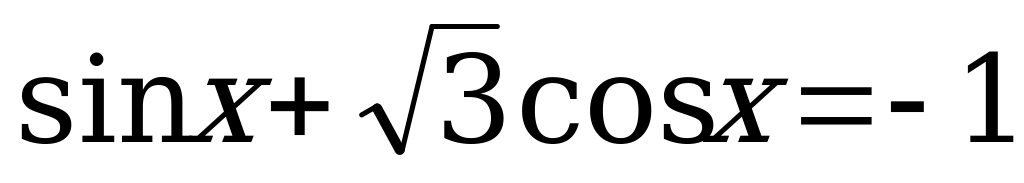
5. 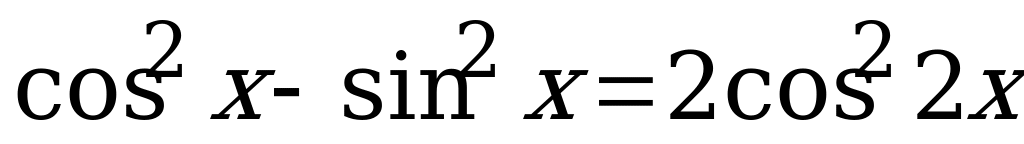
6. 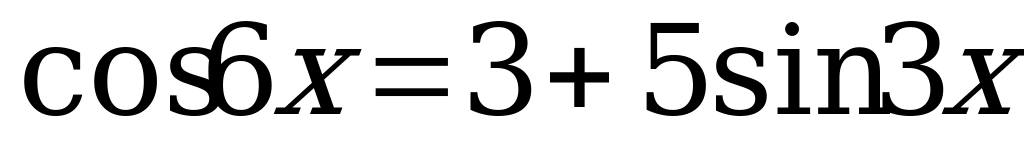
7. 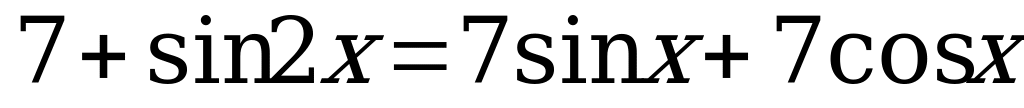 .
.
8. 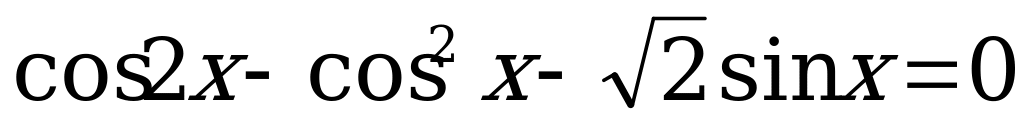 и найдите все его корни, принадлежащие промежутку
и найдите все его корни, принадлежащие промежутку 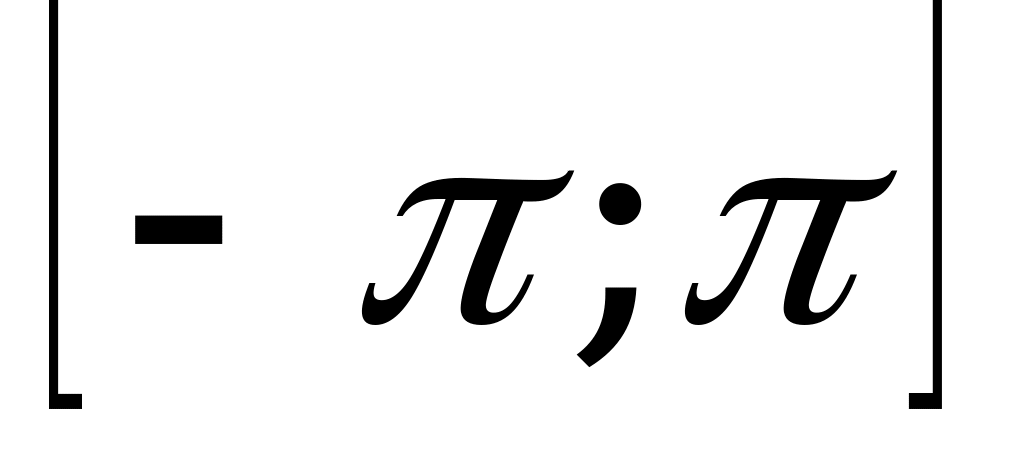 .
.
Вариант № 3 Решите уравнения:
1. 
2. 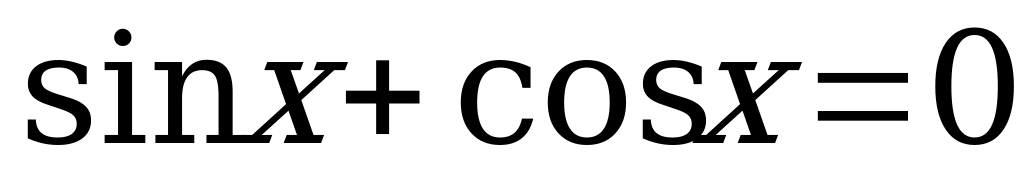
3. 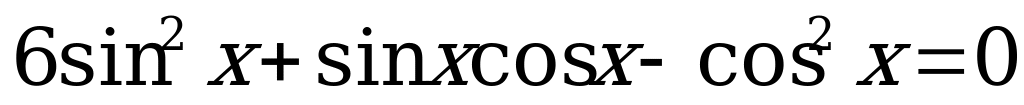
4. 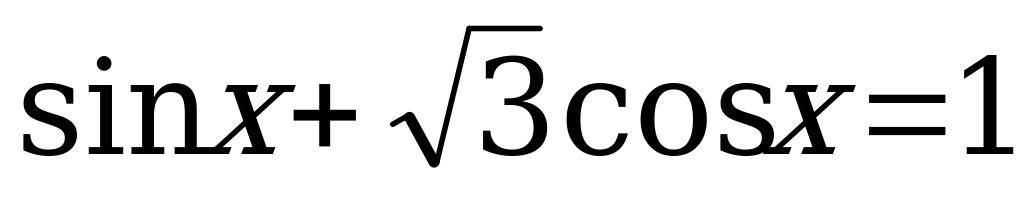
5. 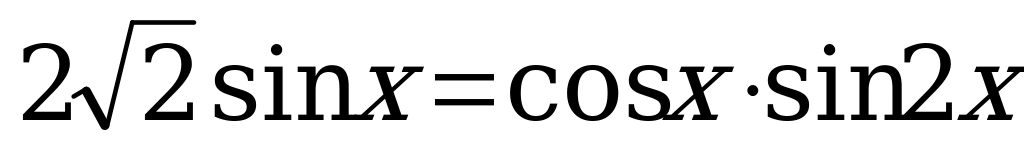
6. 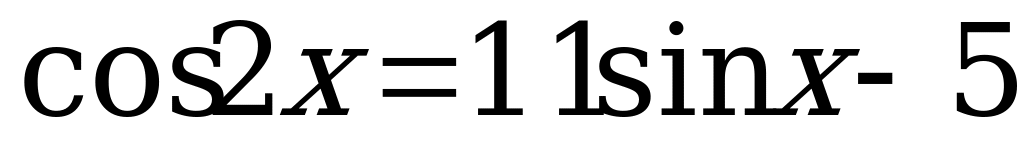
7. 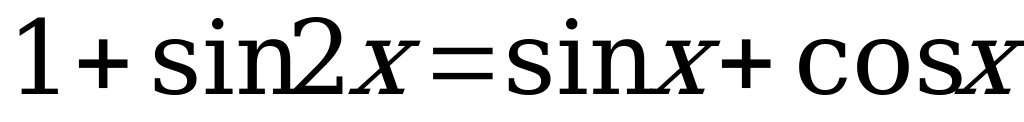
8. 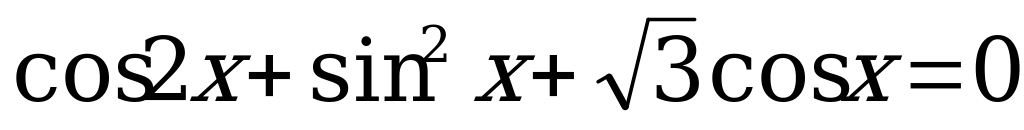 и найдите все его корни, принадлежащие промежутку
и найдите все его корни, принадлежащие промежутку 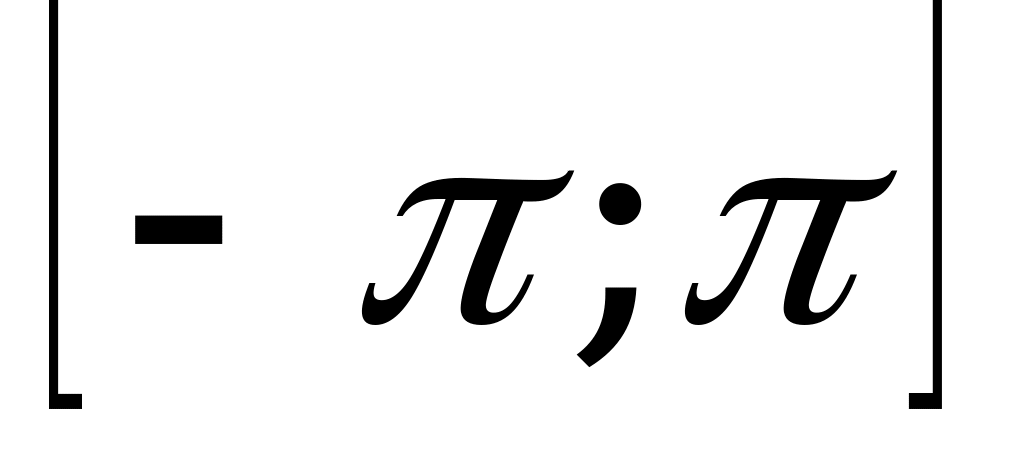 .
.
Вариант № 4 Решите уравнения:
1. 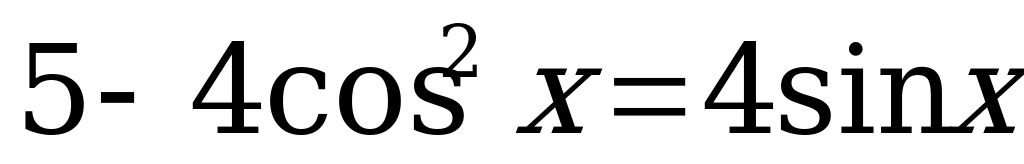
2. 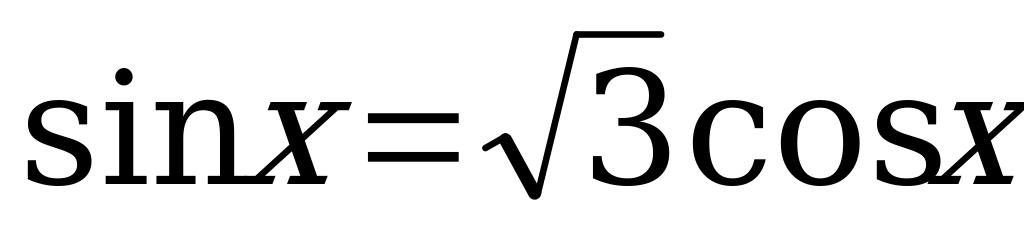
3. 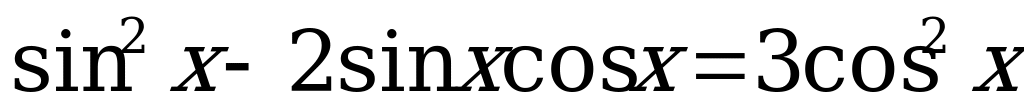
4. 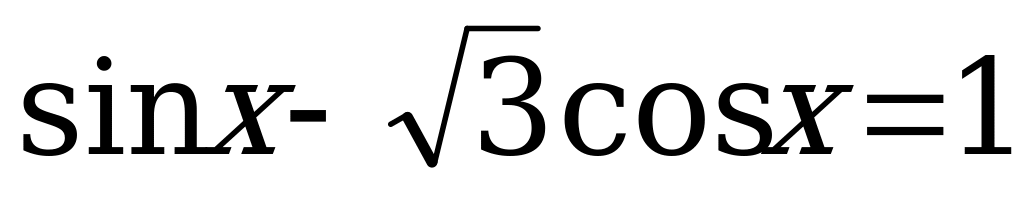
5. 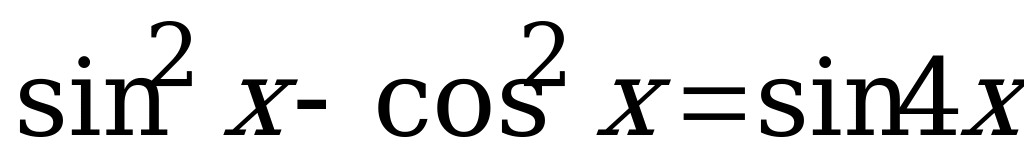
6. 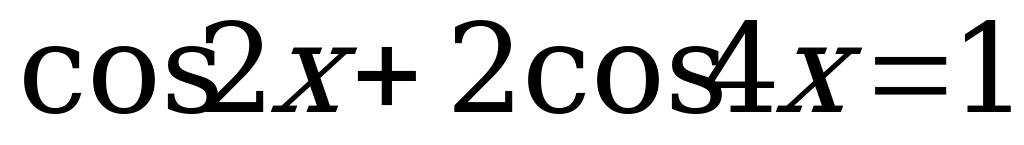
7. 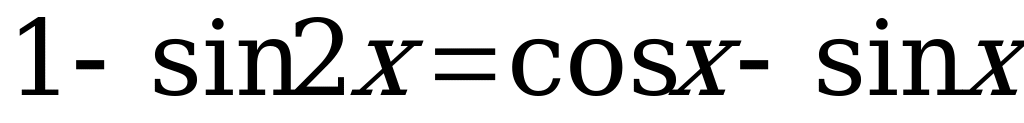
8. 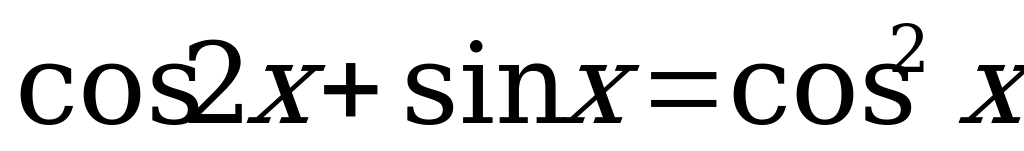 и найдите все его корни, принадлежащие промежутку
и найдите все его корни, принадлежащие промежутку 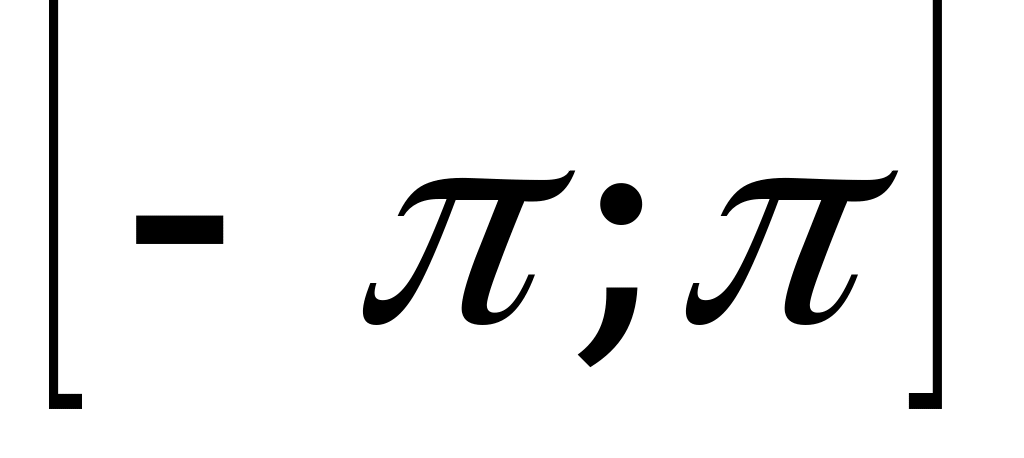 .
.
Самостоятельная работа № 2
по теме «Тригонометрические уравнения»
Вариант № 1 Решите уравнения:
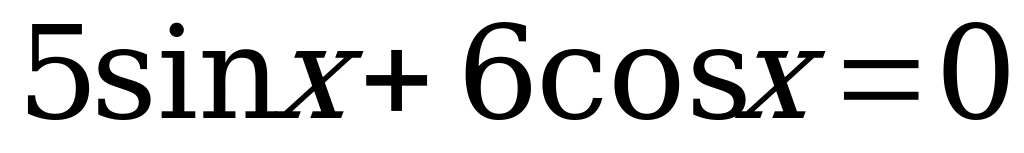
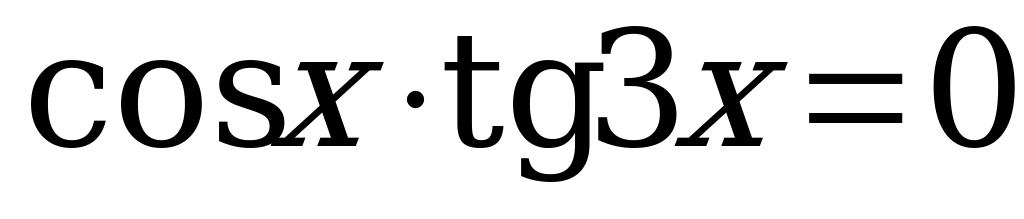
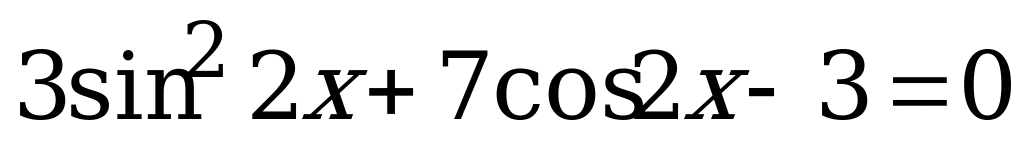
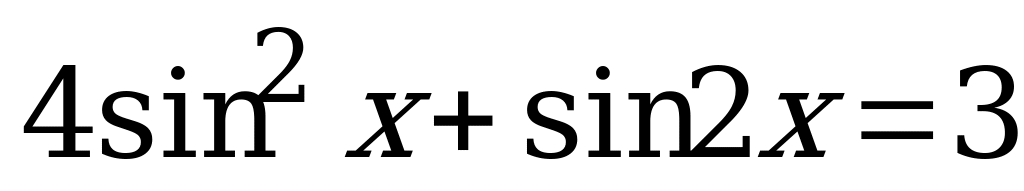
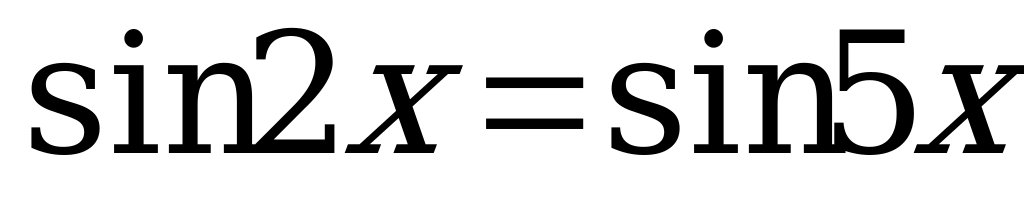
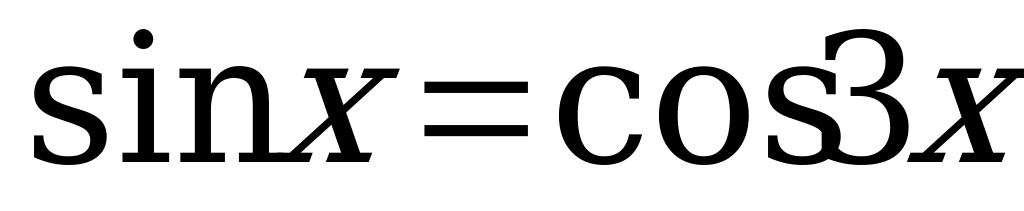
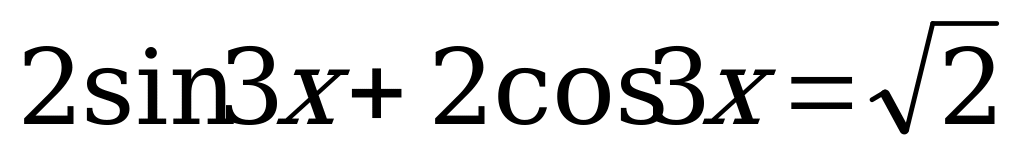
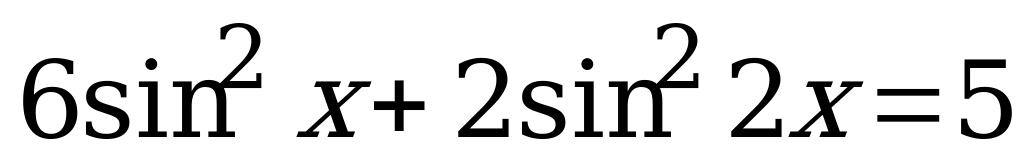
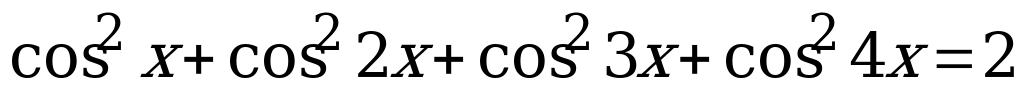
Вариант № 2 Решите уравнения:
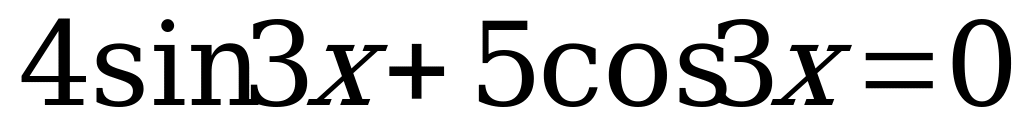
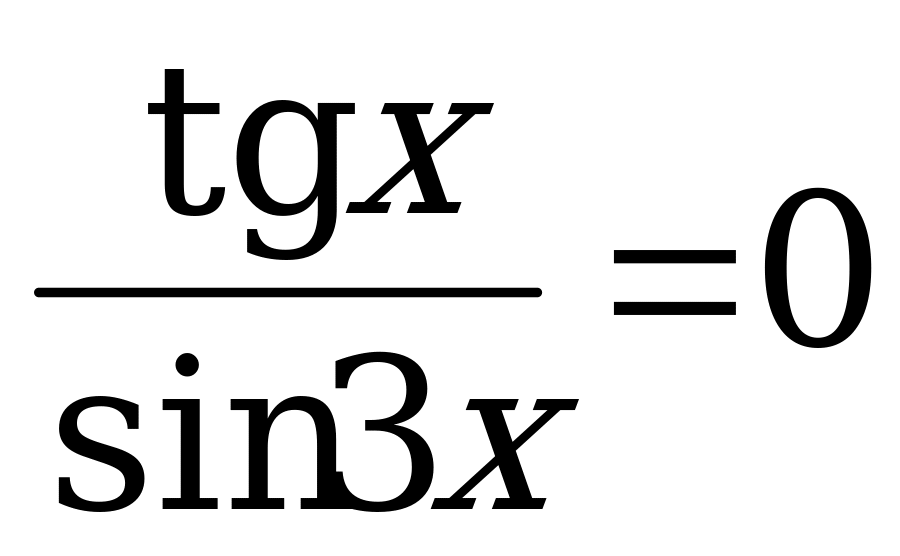
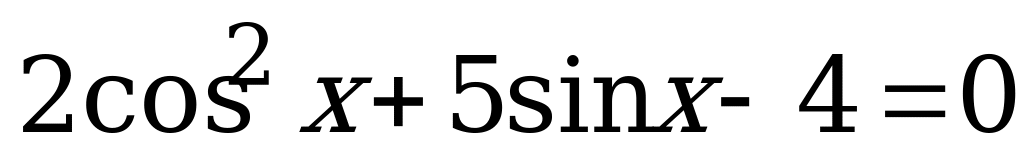
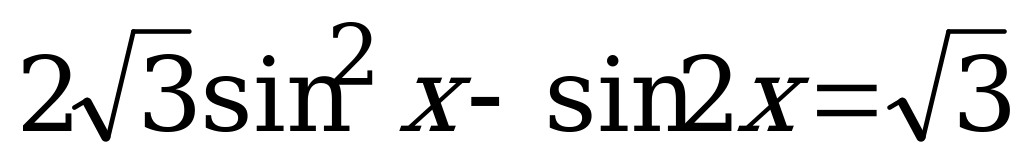
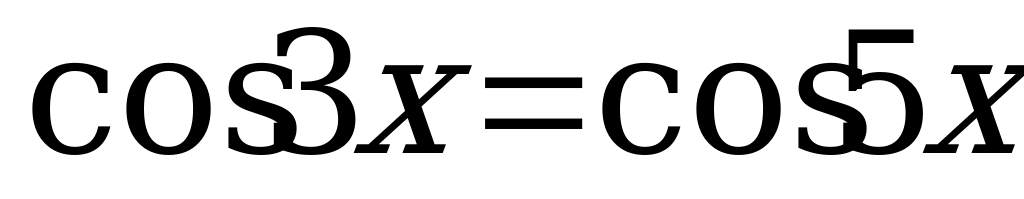
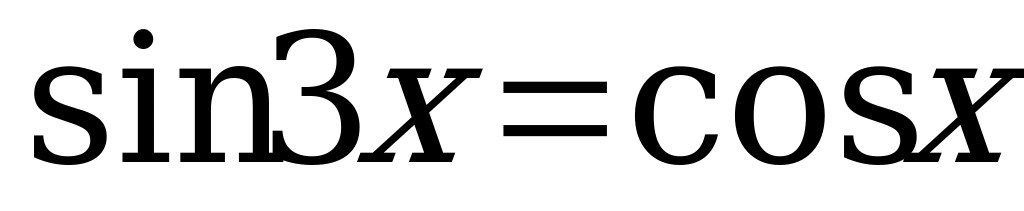
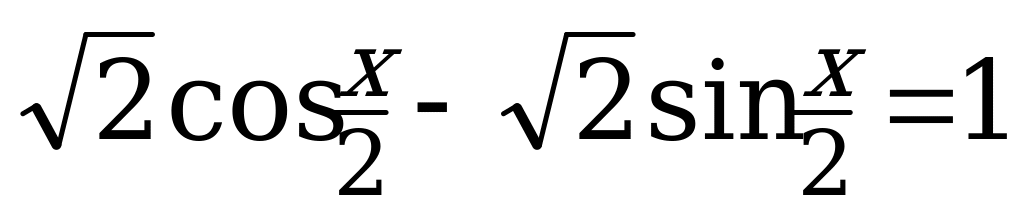
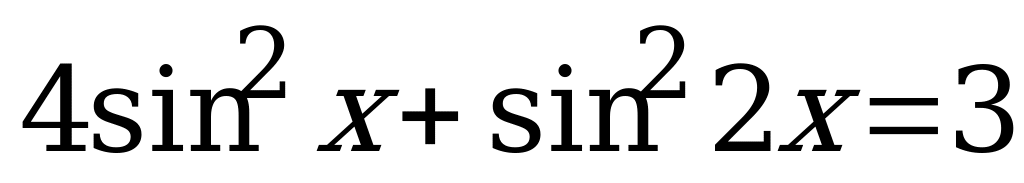
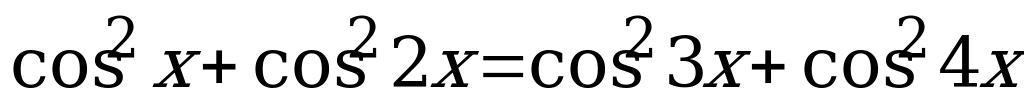
Вариант № 3 Решите уравнения:
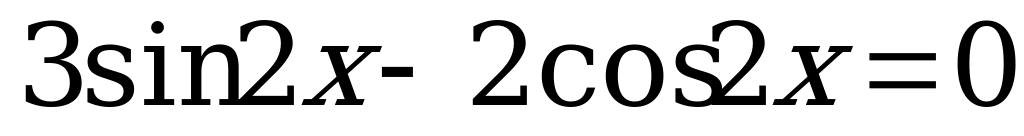
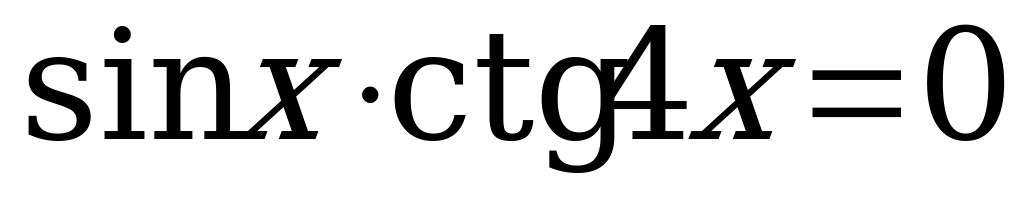
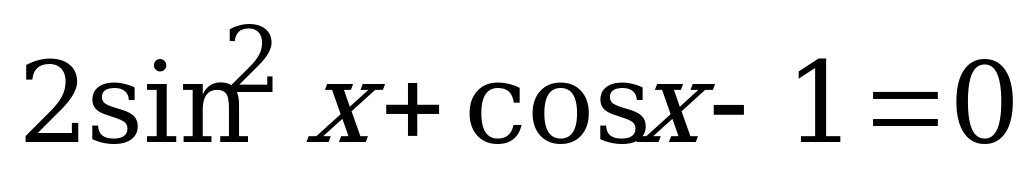
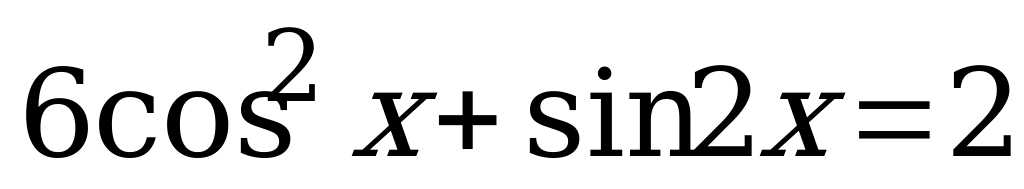
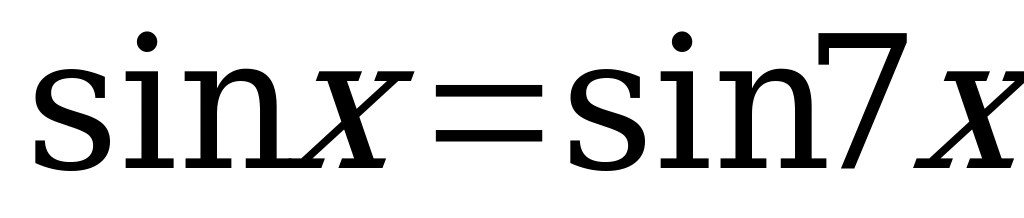
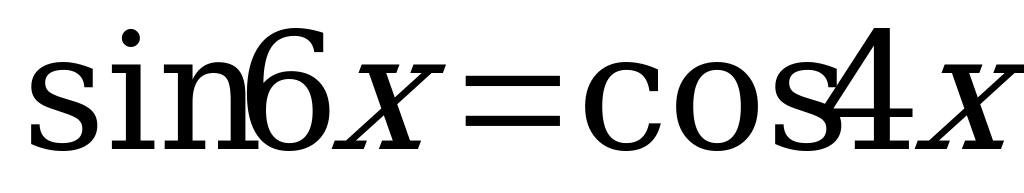
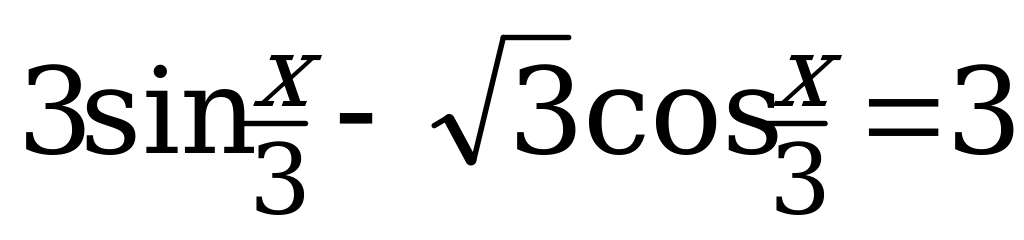
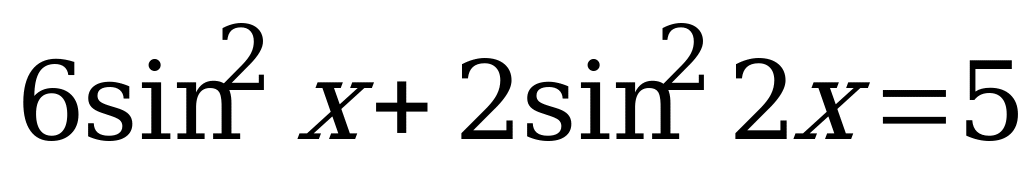
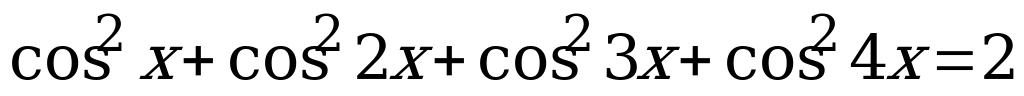
Вариант № 4 Решите уравнения:
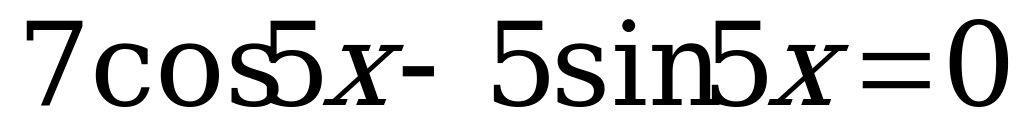
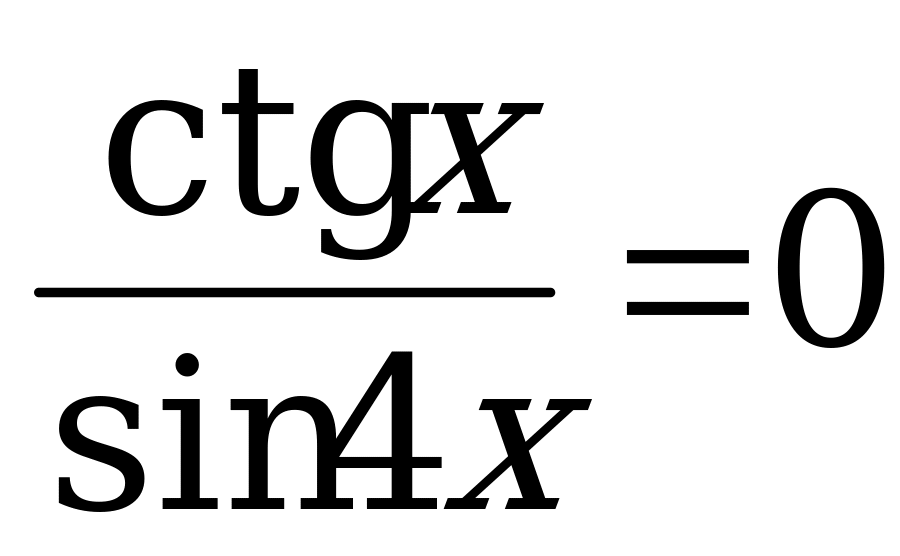

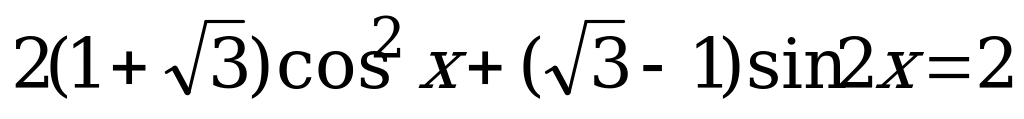
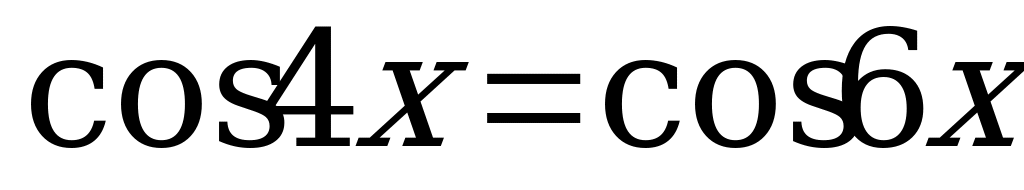
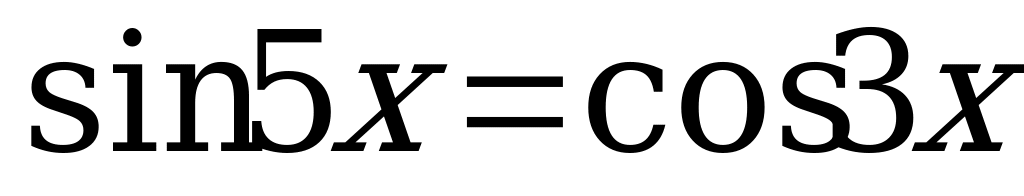
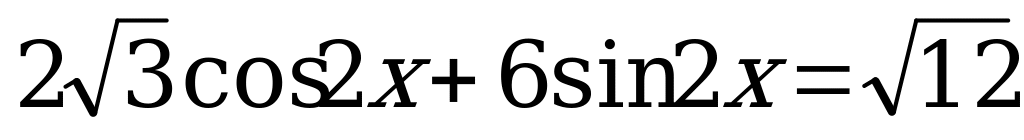
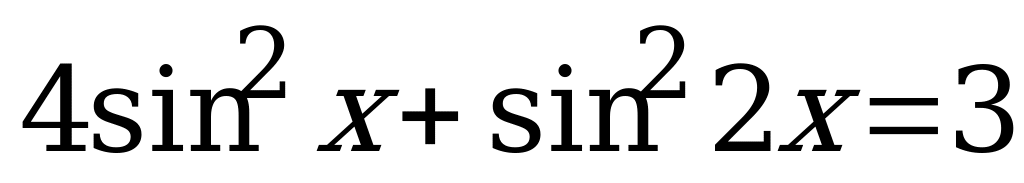
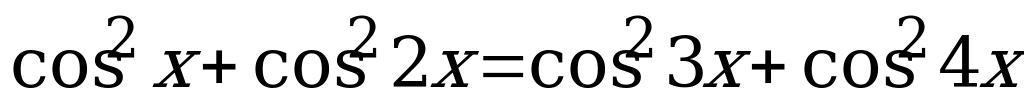
Ответы к самостоятельной работе
| № вар. | 1 | 2 | 3 | 4 | 5 | 6 |
| I | 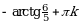 | 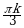 | 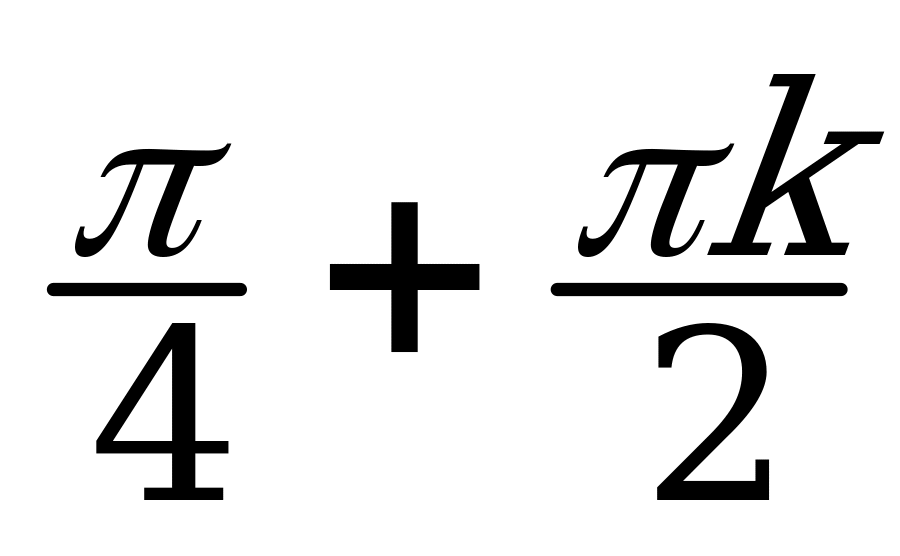 | 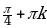 ; ;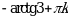 | 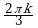 ; ; 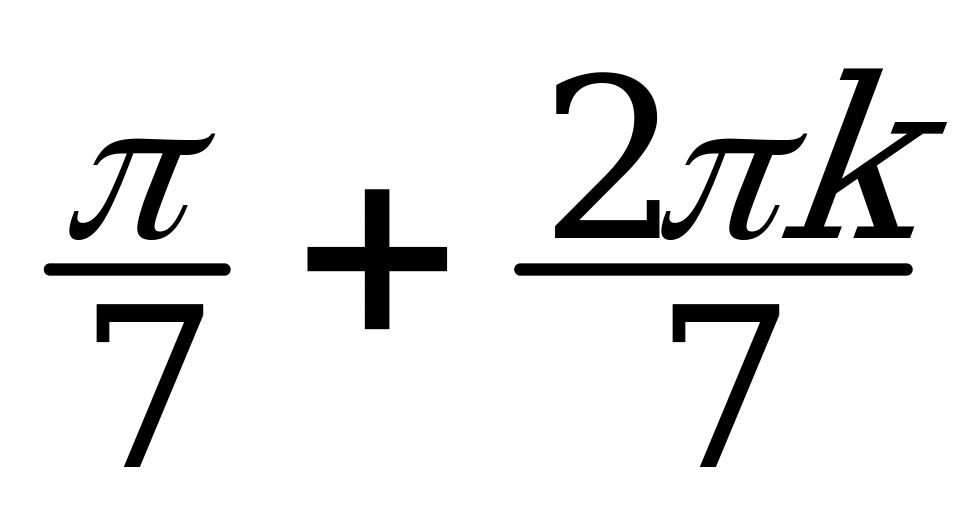 | 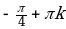 ; ; 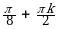 |
| II | 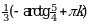 | | 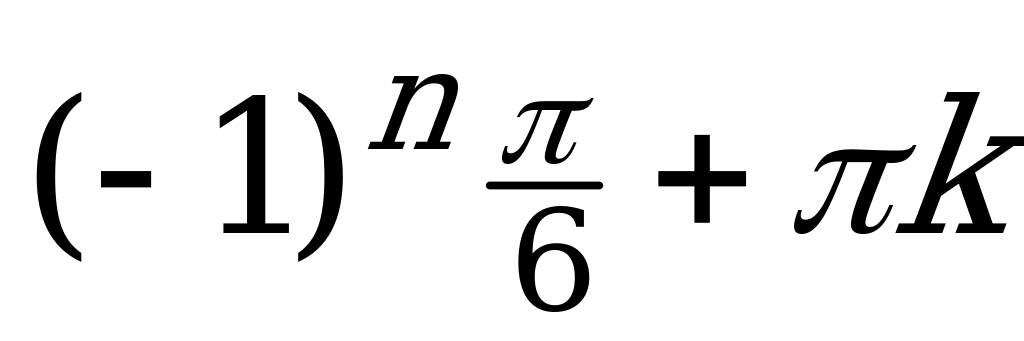 | 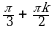 | 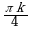 | 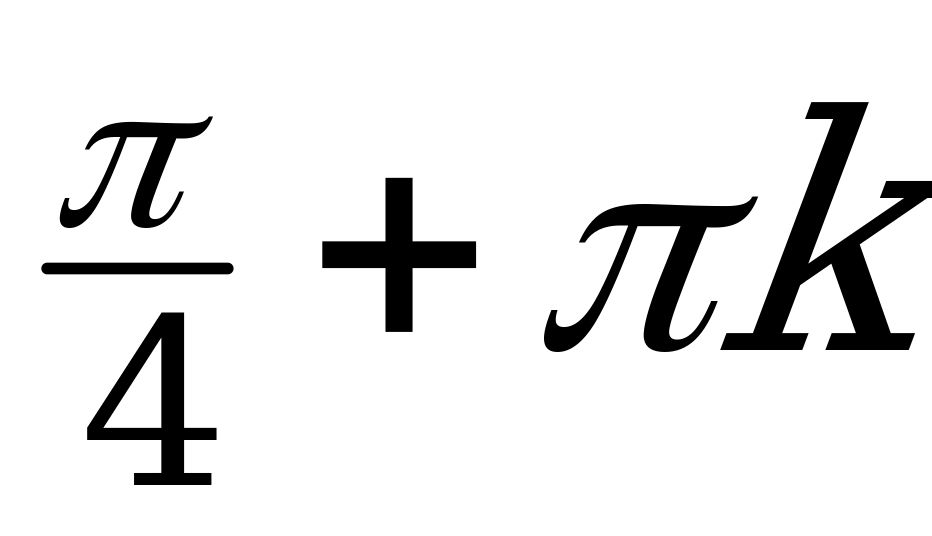 ; ; 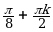 |
| III | 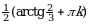 | 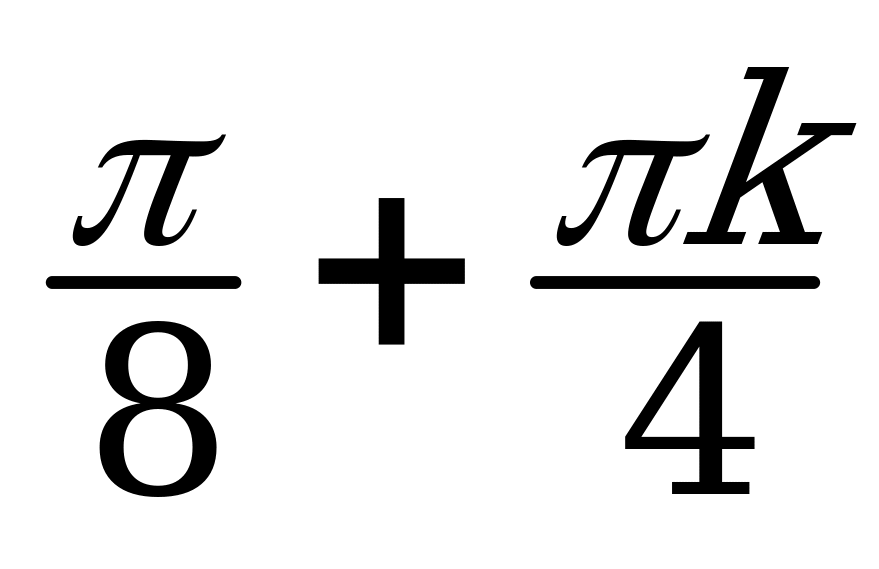 | 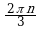 | 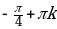 ; ;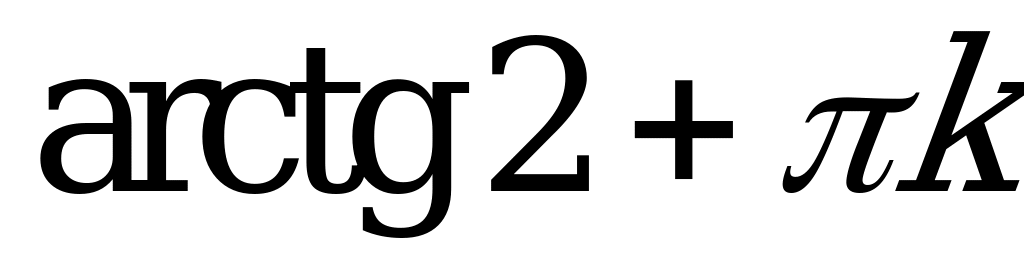 | 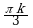 ; ; 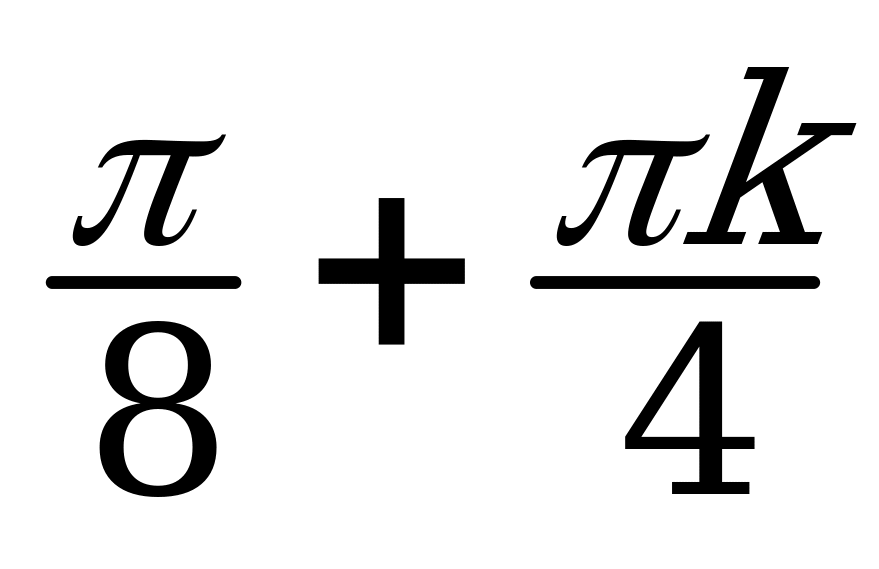 | 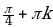 ; ; 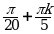 |
| IV | 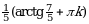 | | 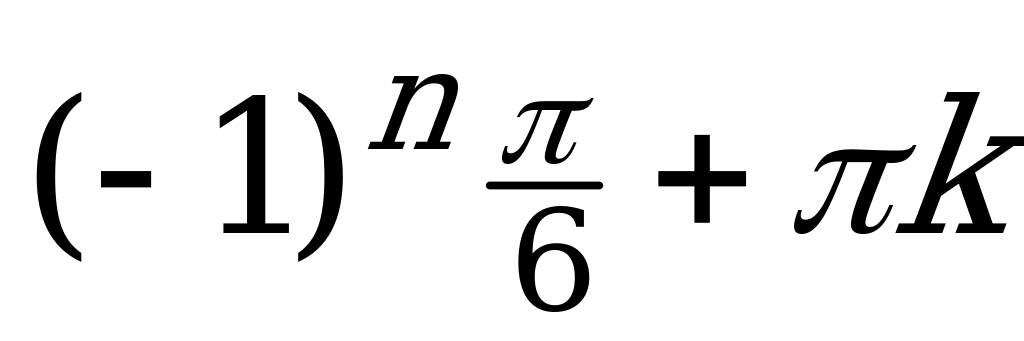 | 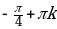 ; ; 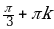 | 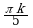 | 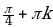 ; ;  |
| баллы | 1 | 2 | 2 | 2 | 2 | 2 |
| номер
вар. | 7 | 8 | 9 |
| I | 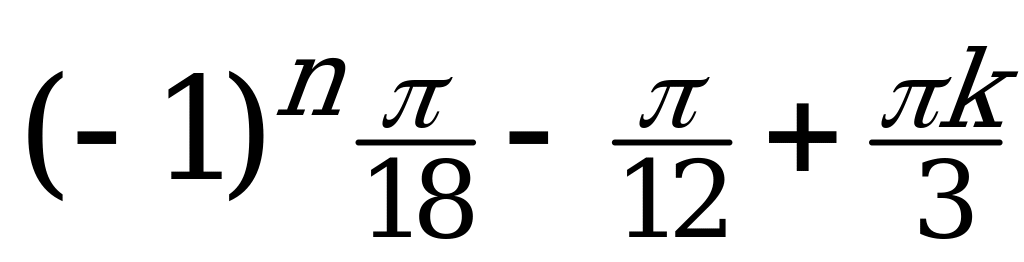 | 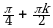 | 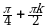 ; ; 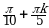 ; ; 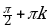 |
| II | 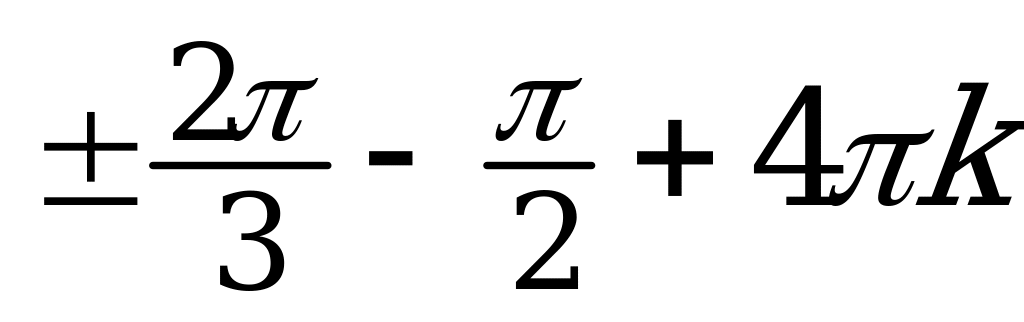 | 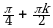 | 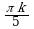 ; ; 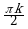 |
| III | 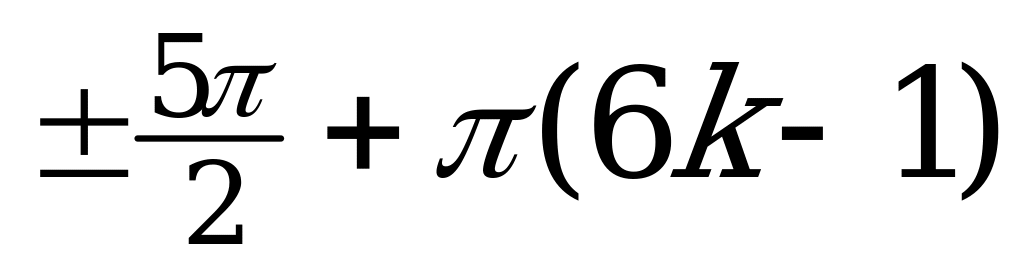 | 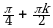 | 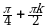 ; ; 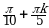 ; ; 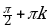 |
| IV | 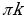 ; ; 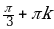 | 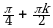 | 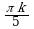 ; ; 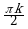 |
| баллы | 3 | 3 | 3 |
Обучающий тренажер и итоговый тест по теме
«Решение тригонометрических уравнений»
Обучающий тренажер по теме «Тригонометрические уравнения»
Найдите решение уравнения на указанном промежутке:
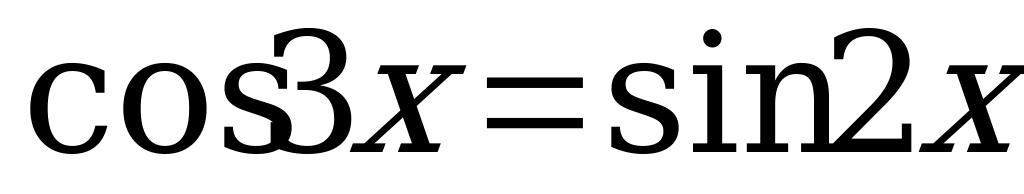 ,
, 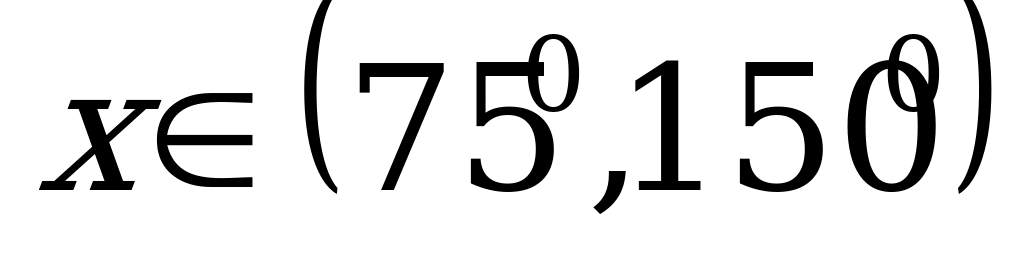 (
(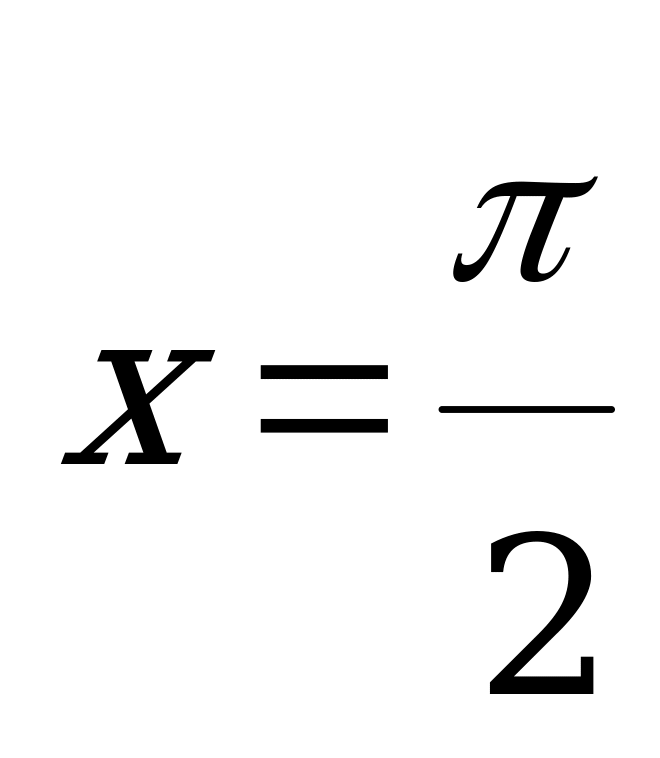 )
)
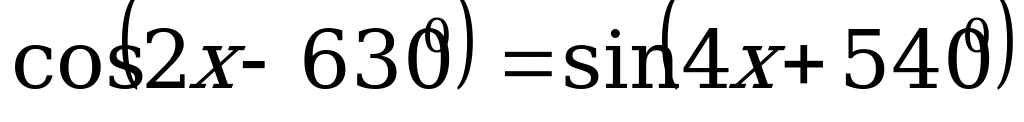 ,
, 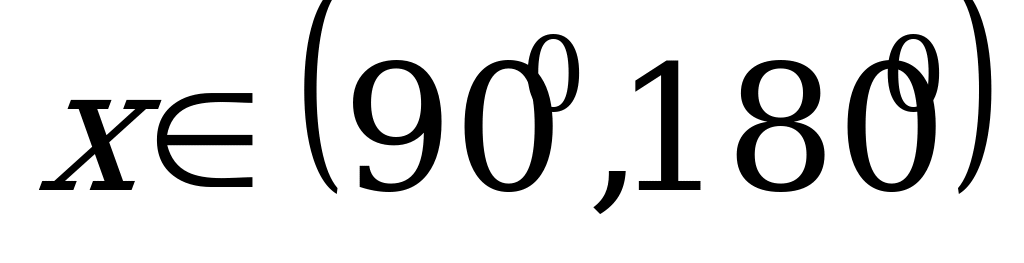 (
(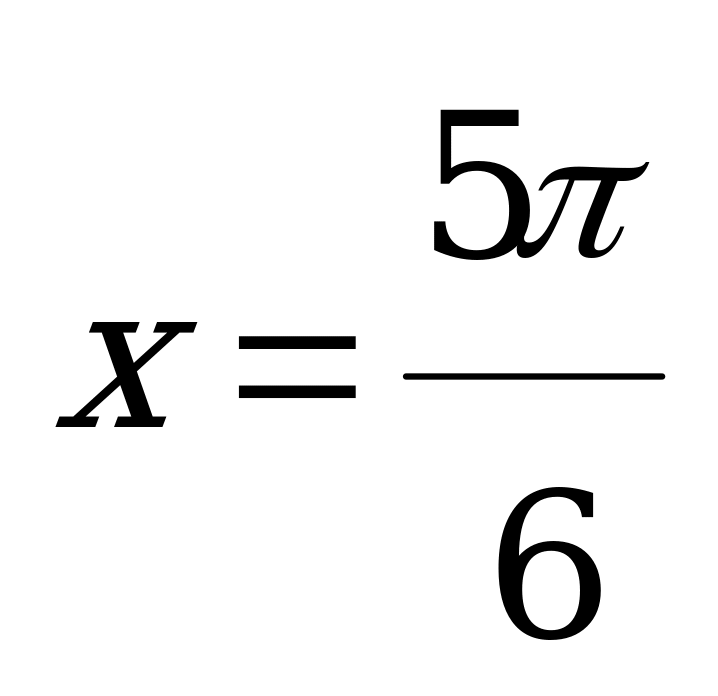 )
)
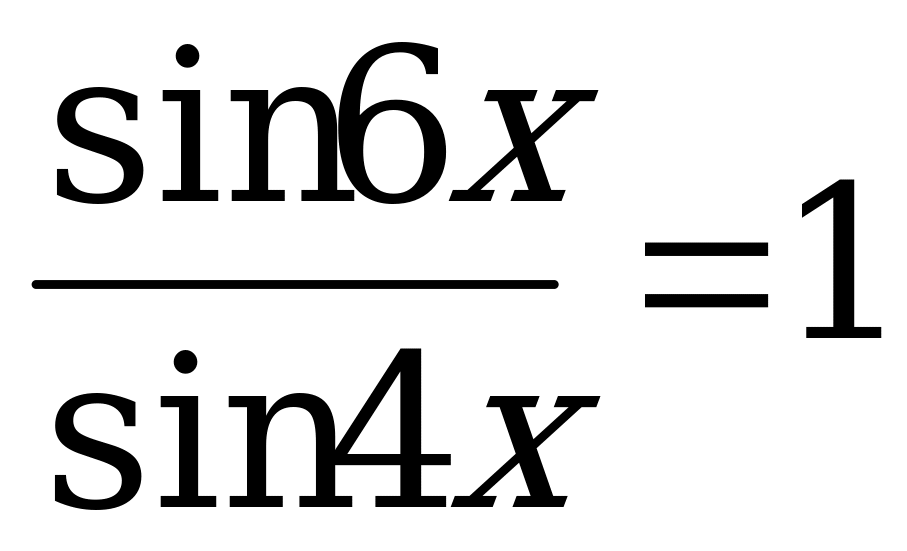 ,
, 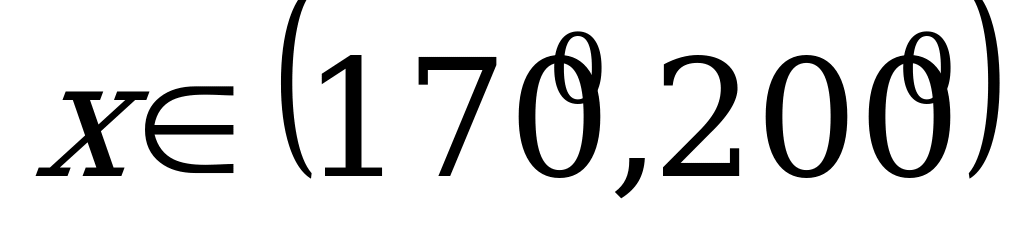 (
(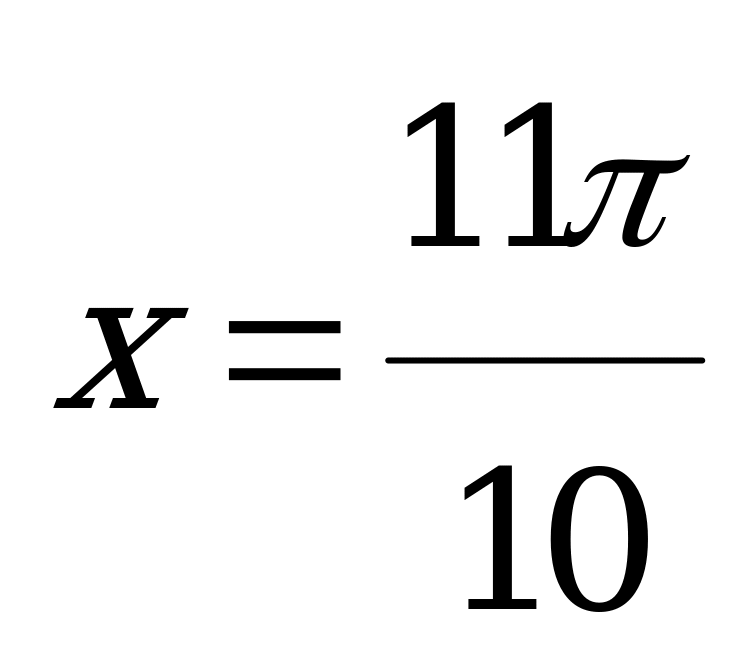 )
)
II. Решите уравнение:
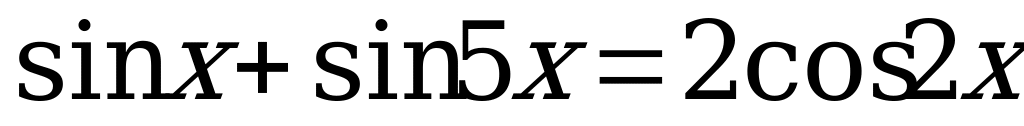 (
(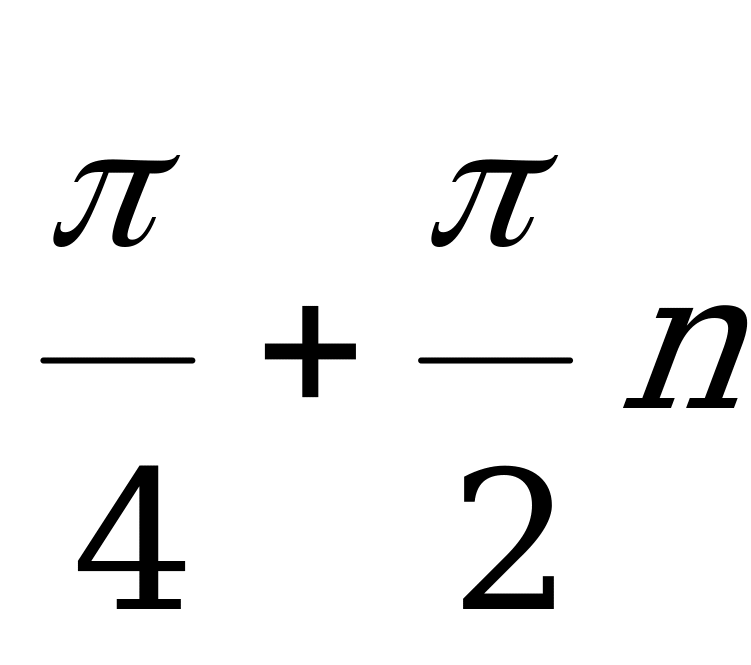 ,
, 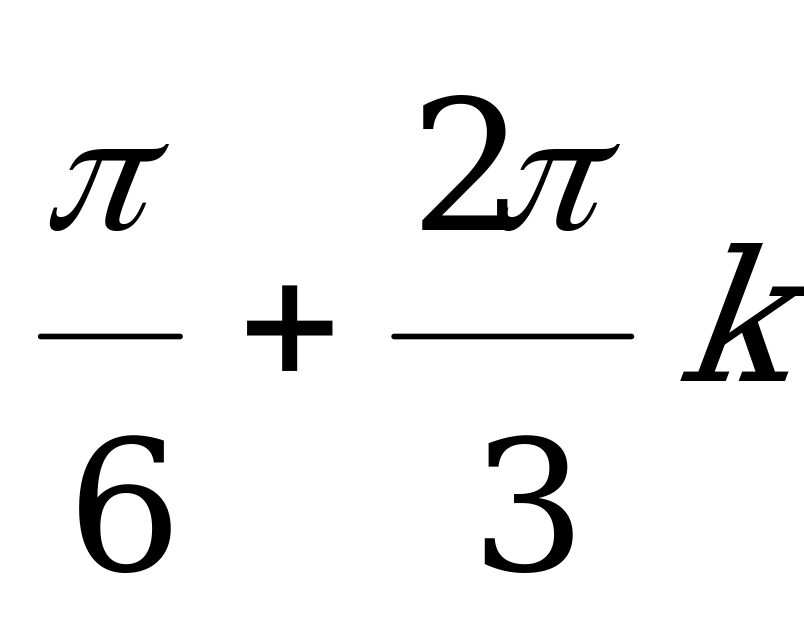 )
)
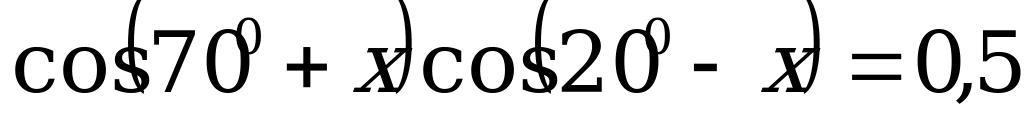 (
(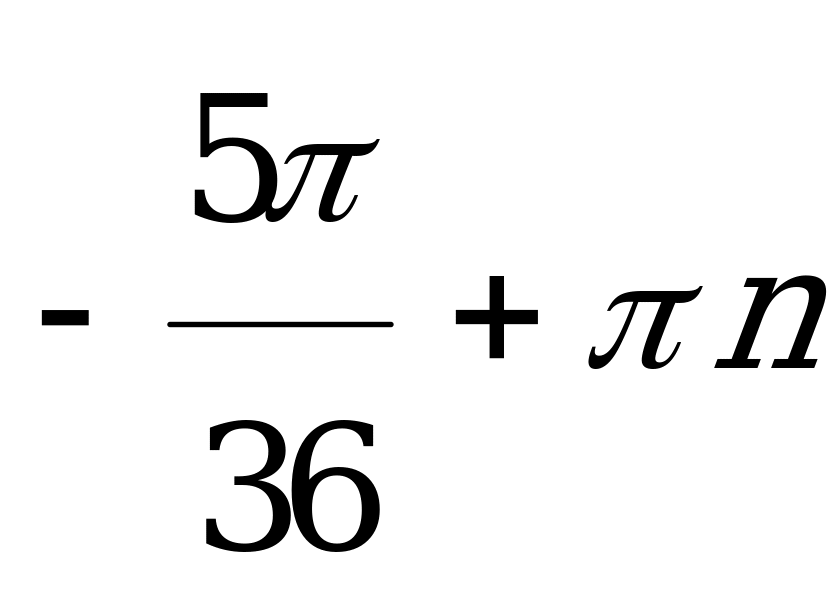 )
)
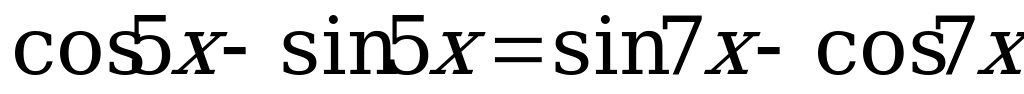 (
(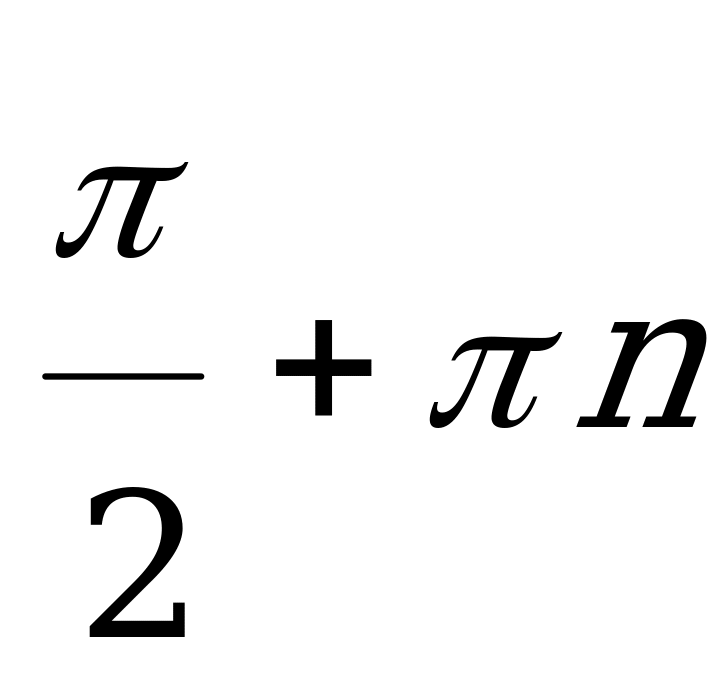 ,
, 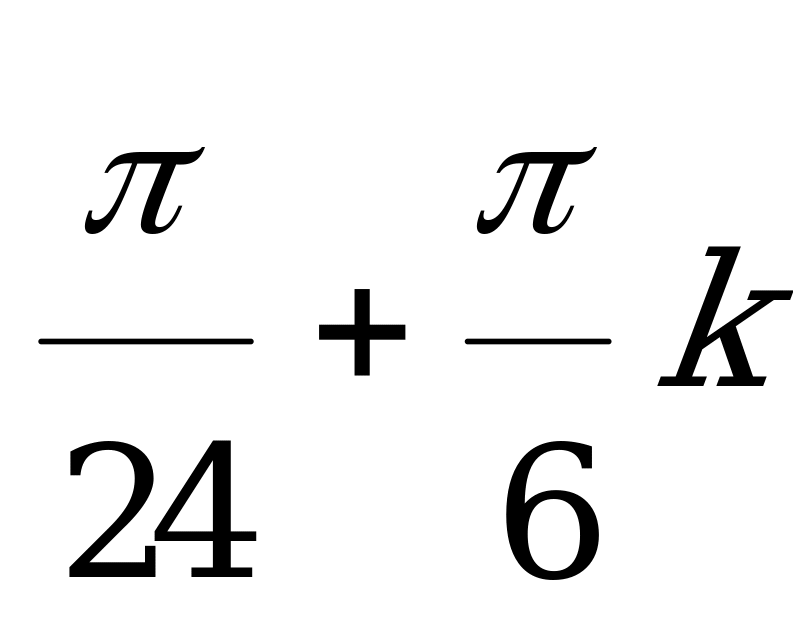 )
)
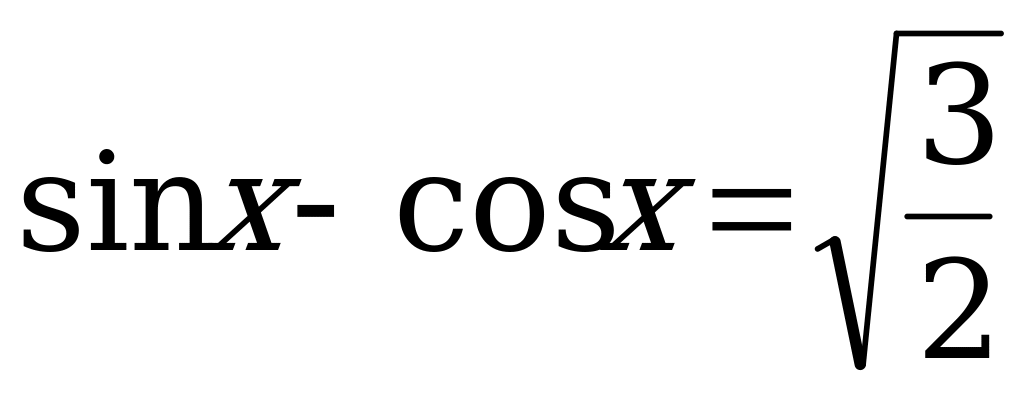 (
(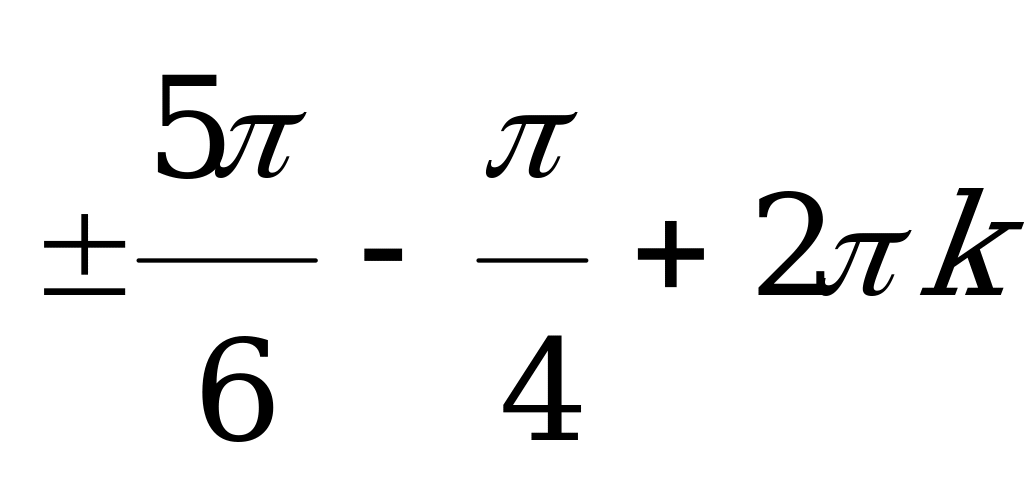 //
// 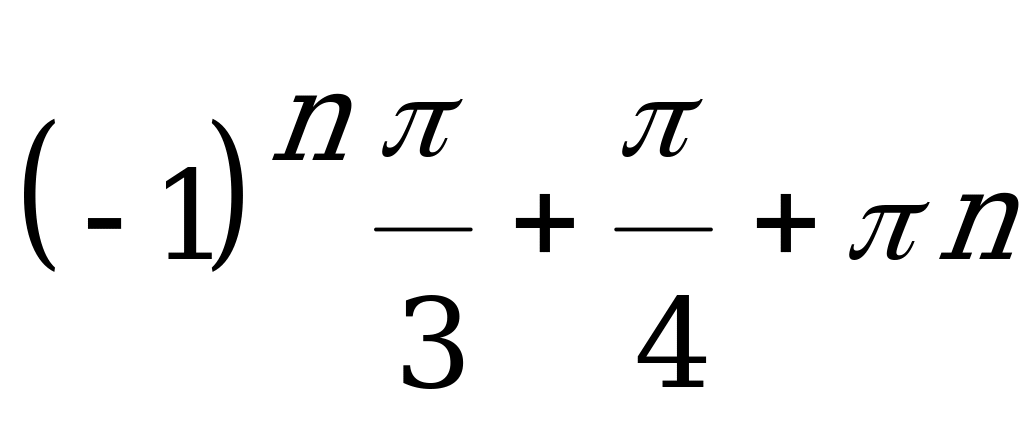 )
)
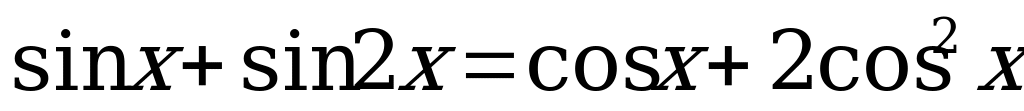 (
(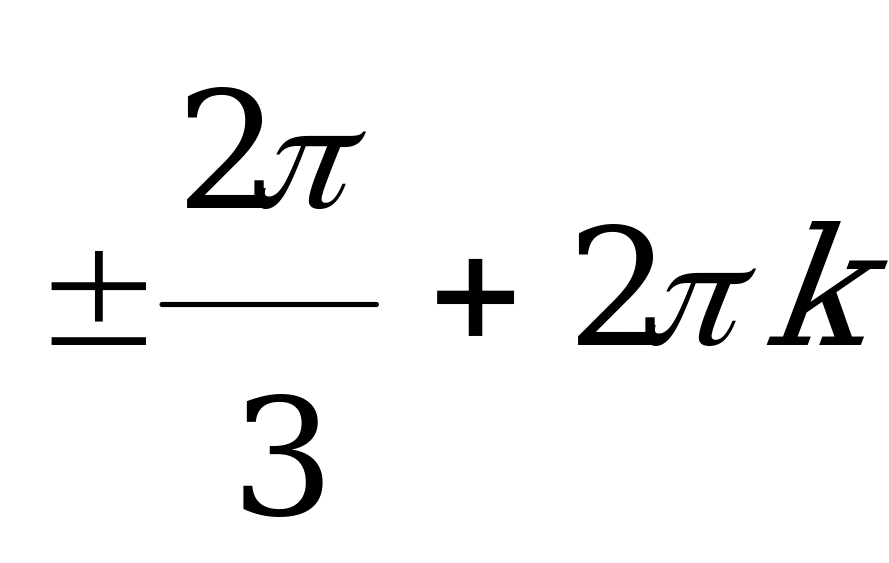 ,
, 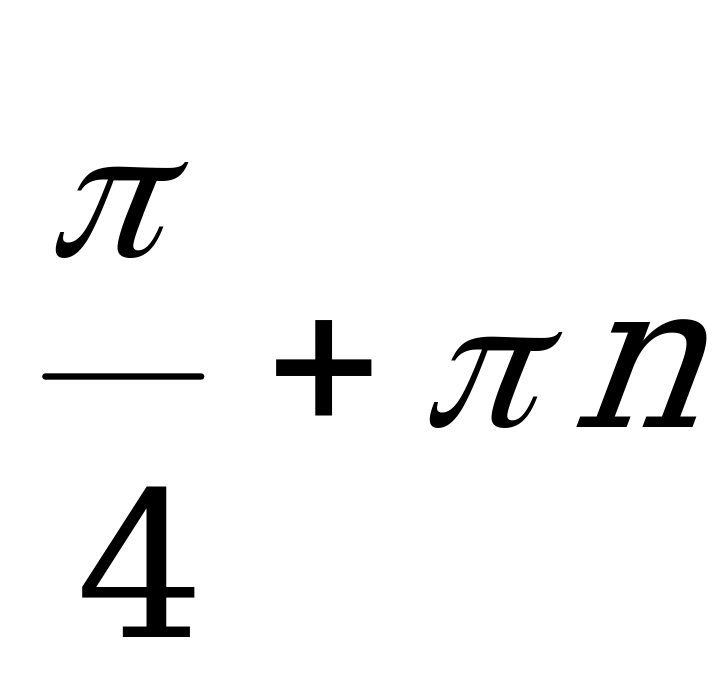 )
)
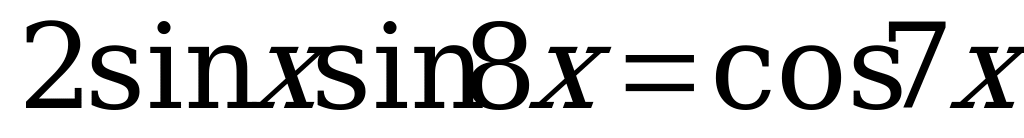 (
(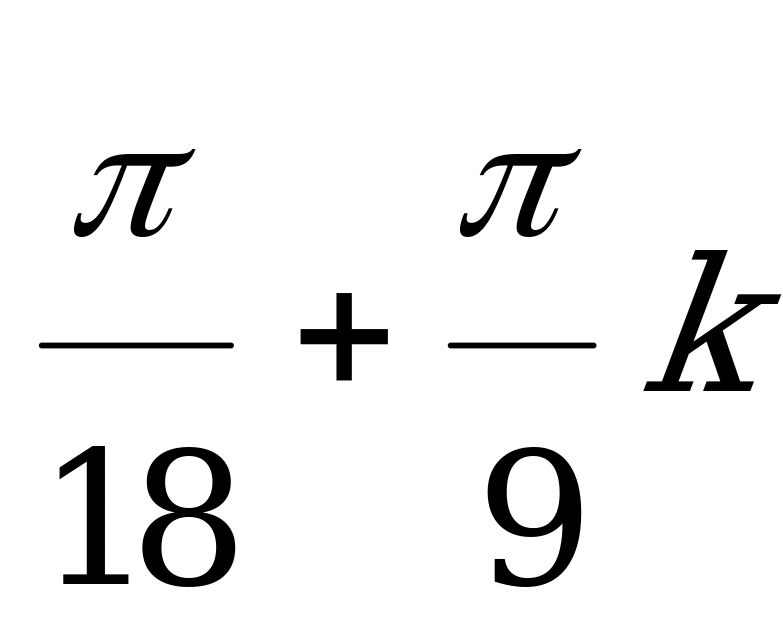 )
)
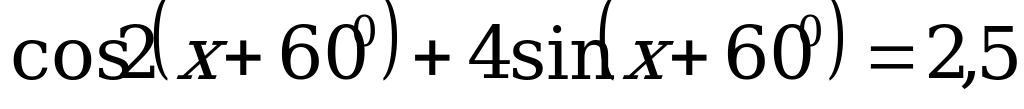 (
(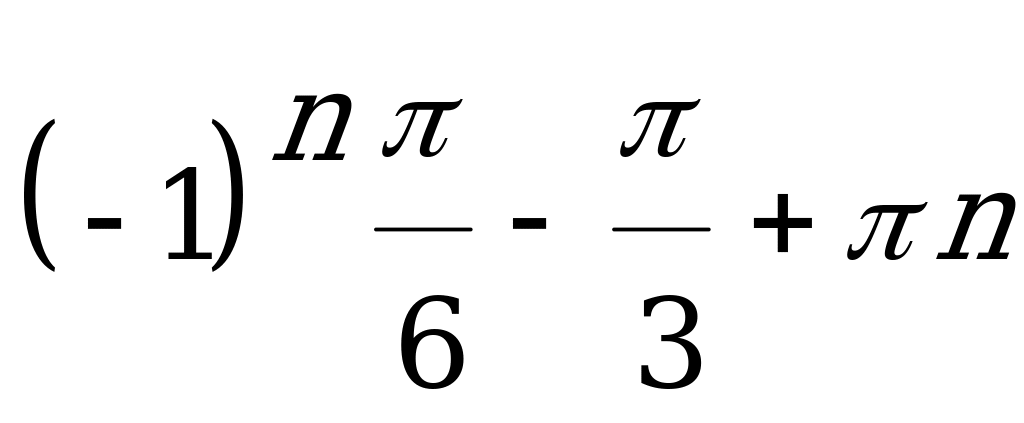 )
)
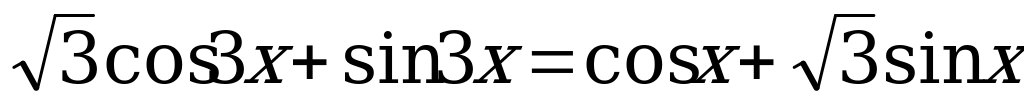 (
(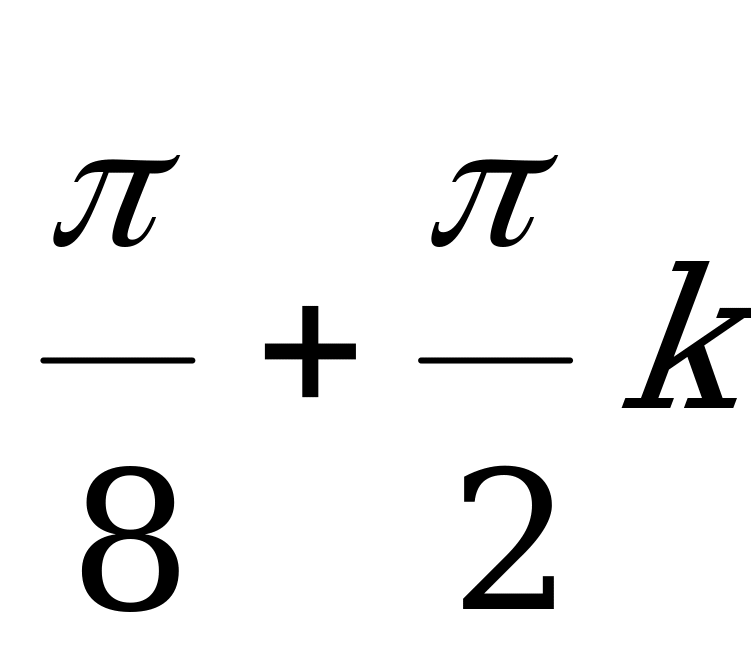 ,
, 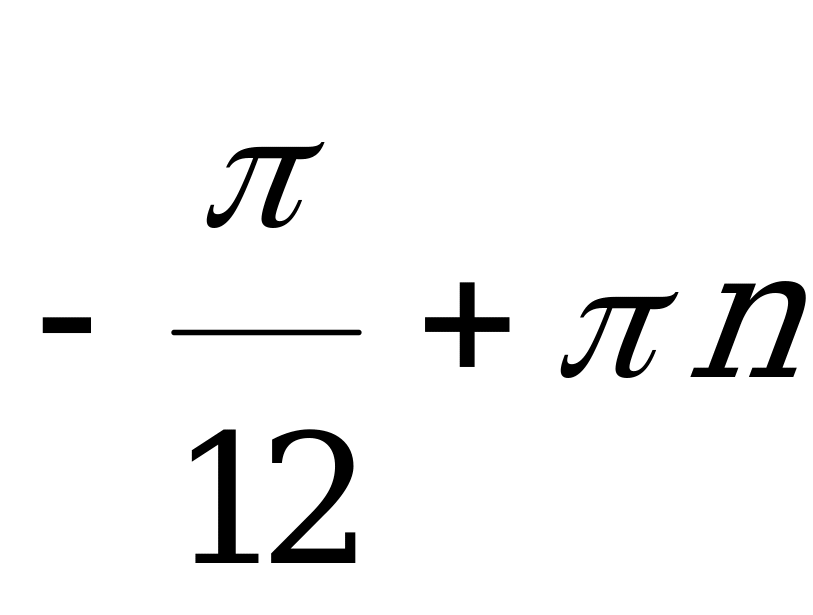 )
)
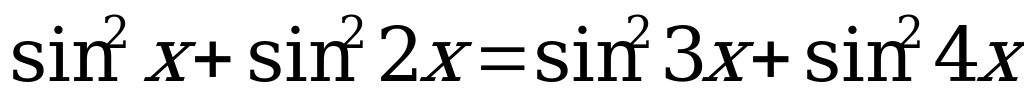 (
(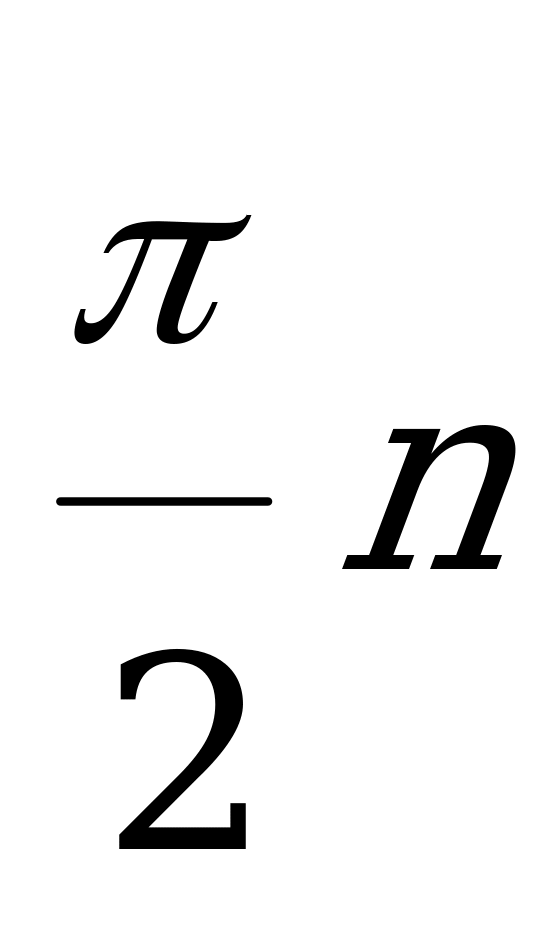 ,
, 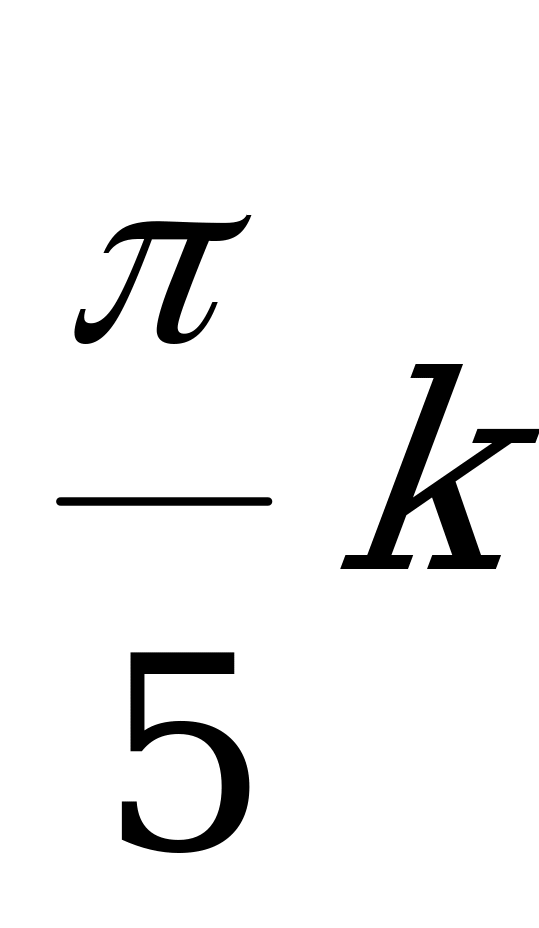 )
)
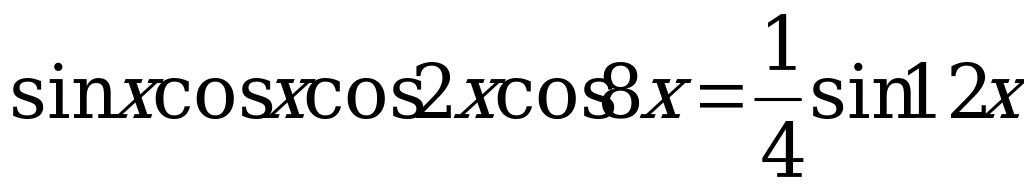 (
(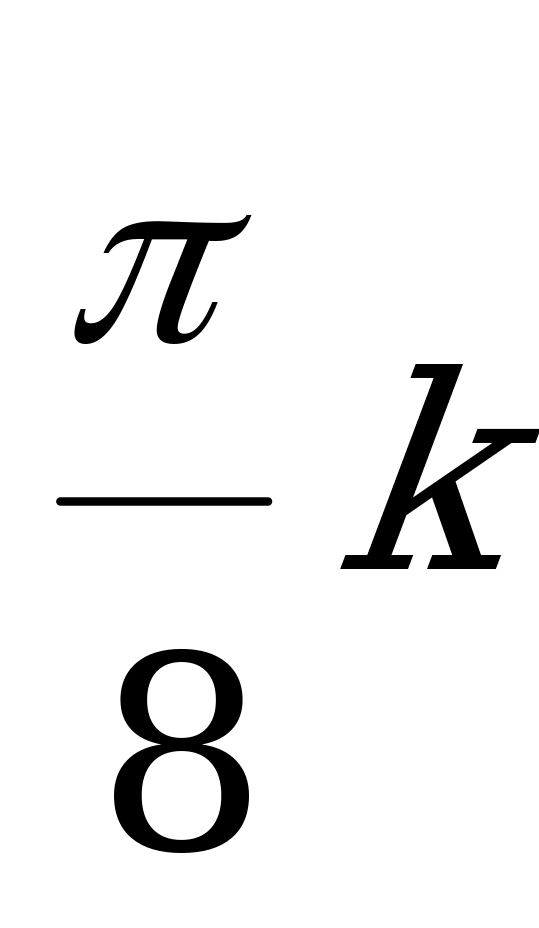 )
)
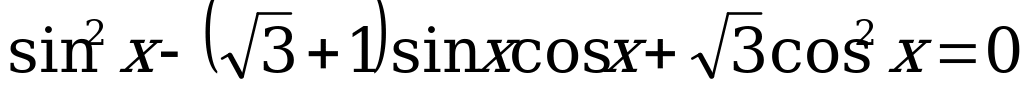 (
(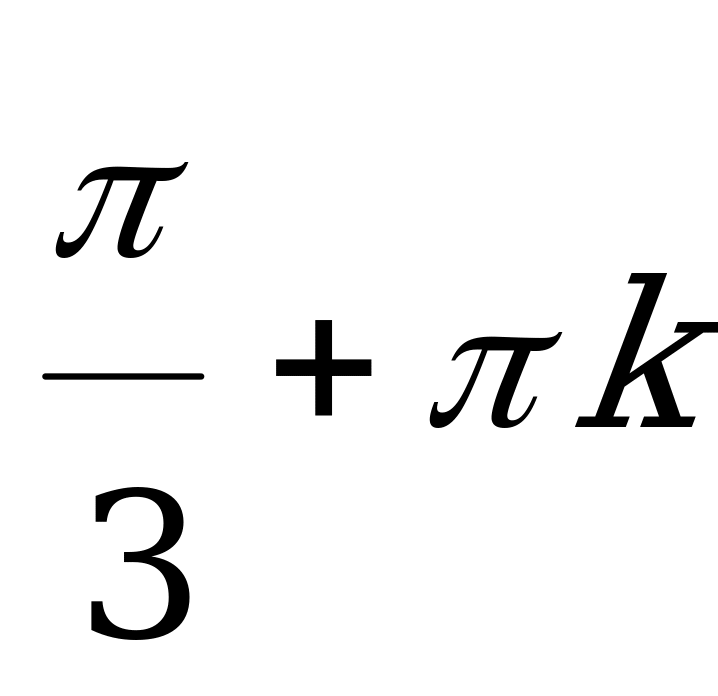 ,
, 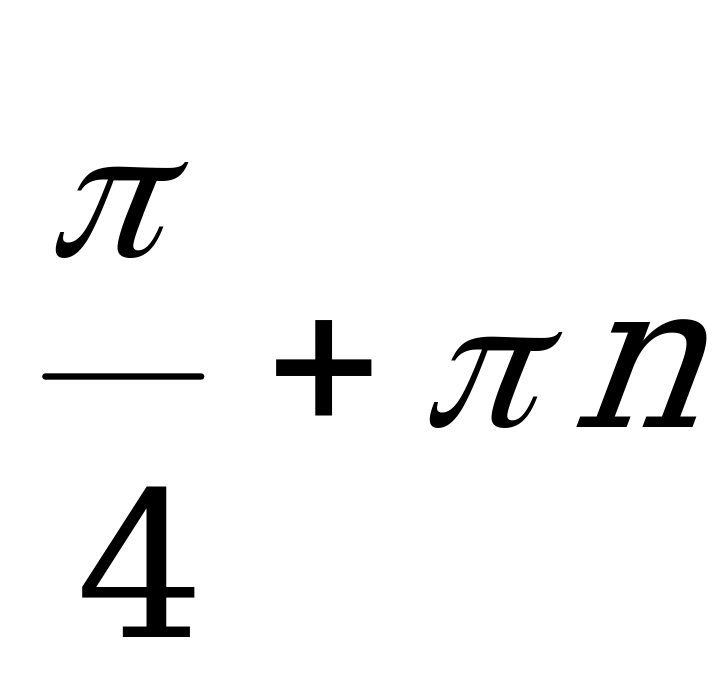 )
)
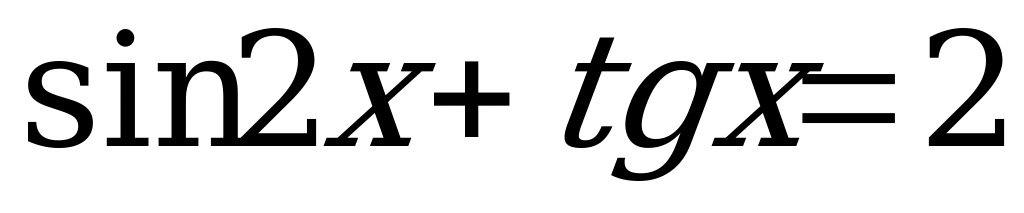 (
( )
)
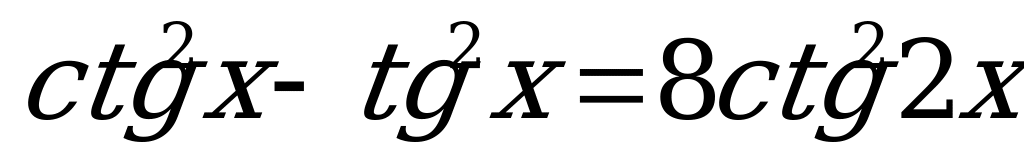 (
(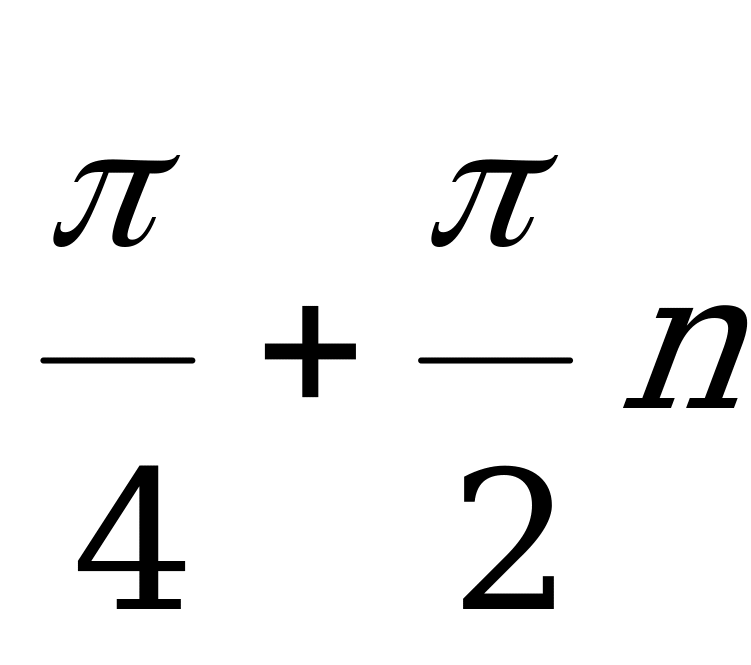 ,
, 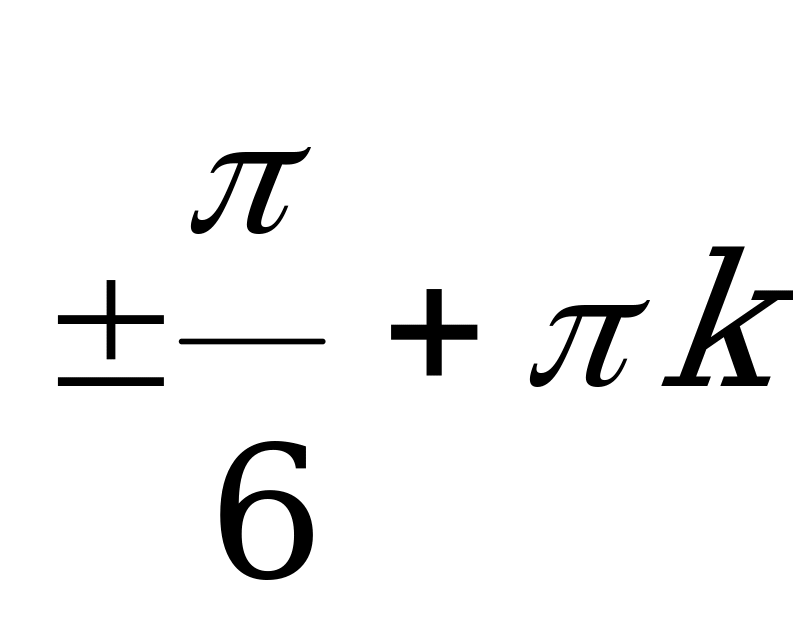 )
)
Найти число корней уравнения 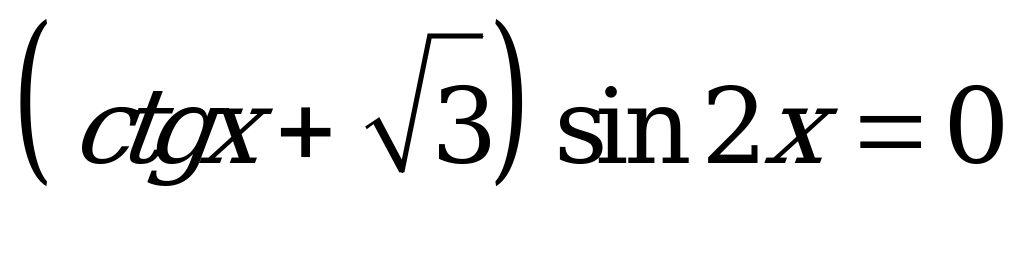 , принадлежащих интервалу
, принадлежащих интервалу 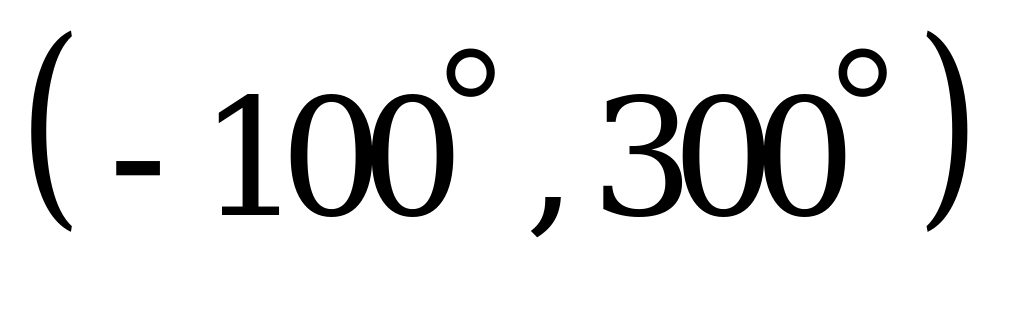 . (5)
. (5)
Итоговый тест по теме
«Решение тригонометрических уравнений»
Найдите (в градусах) сумму корней уравнения 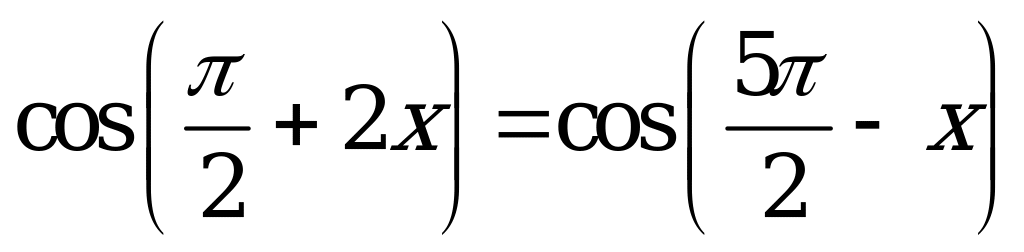 , принадлежащих интервалу
, принадлежащих интервалу 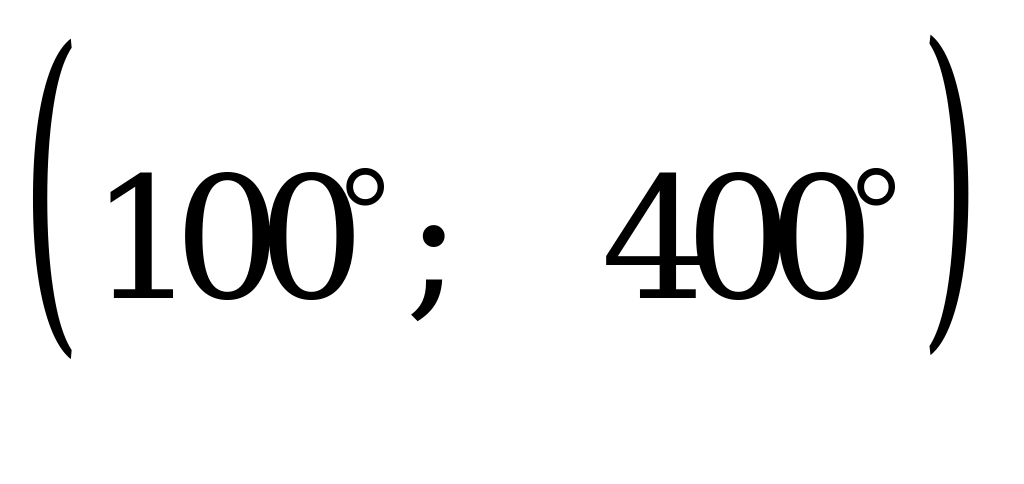
А) 280° B) 360° C) 540° D) 680° E) 900°
Сумма корней уравнения 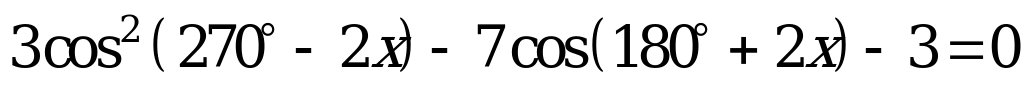 , принадлежащих интервалу
, принадлежащих интервалу 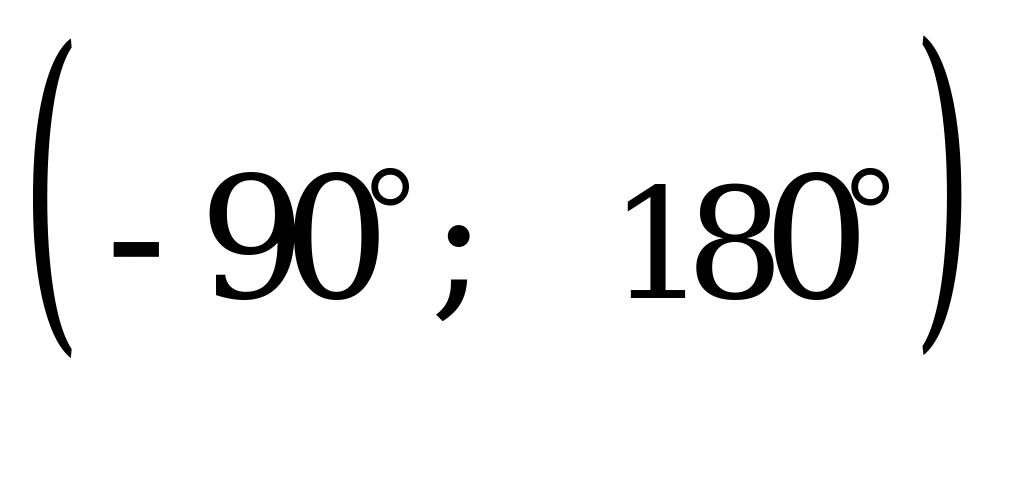
А) 90° B) 150° C) 105° D) 180° E) 135°
Среднее арифметическое всех корней уравнения 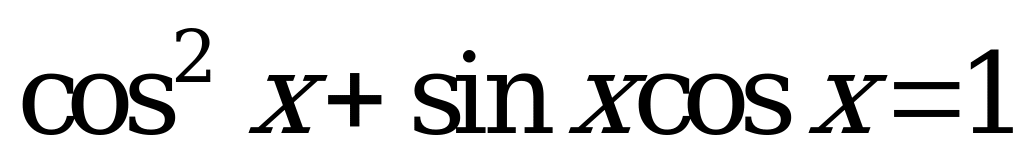 , принадлежащих промежутку
, принадлежащих промежутку 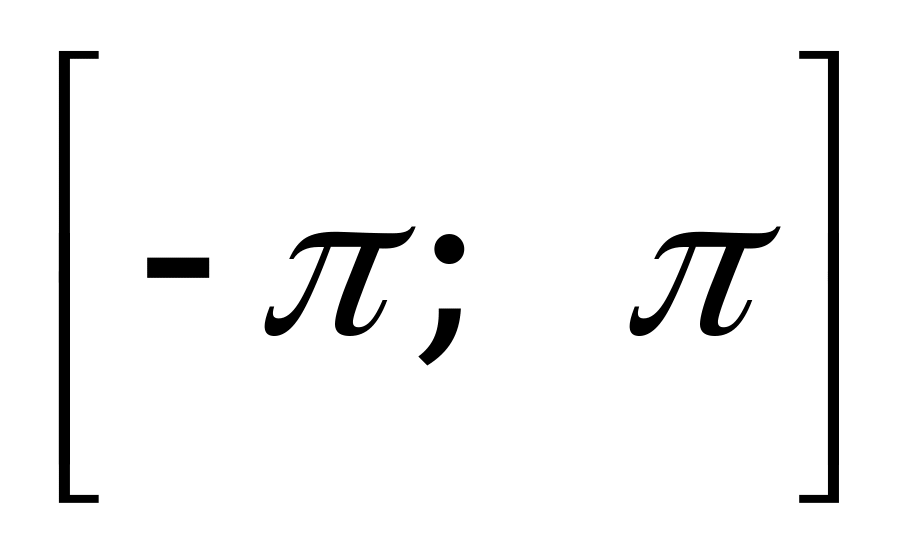 , равно
, равно
А) 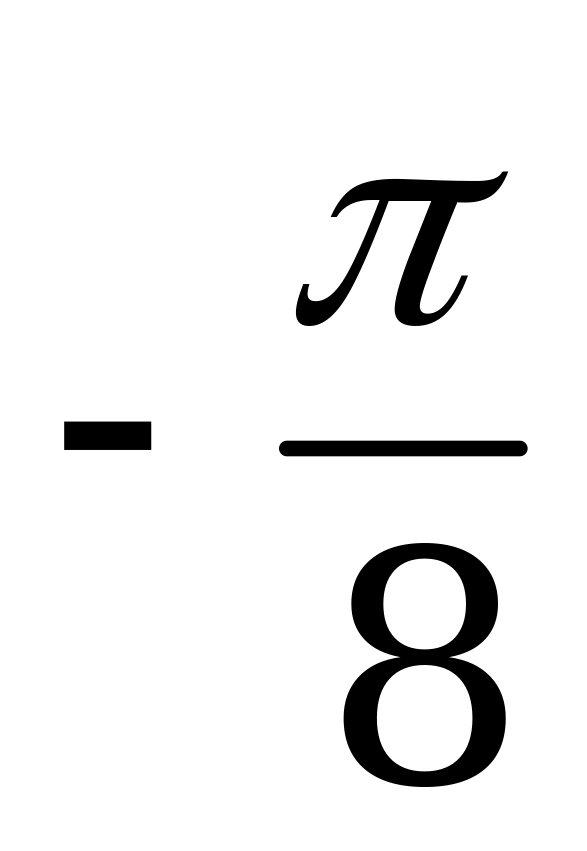 B) 0 C)
B) 0 C)  D)
D) 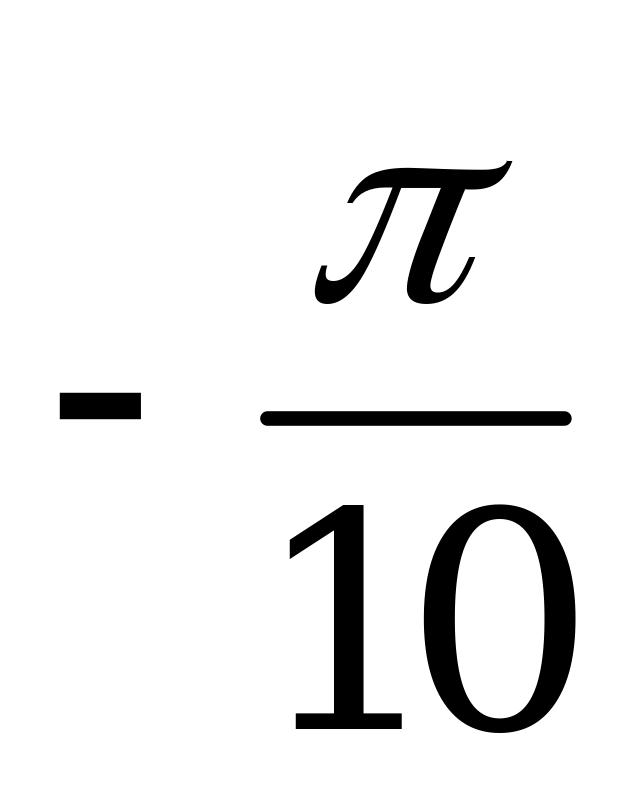 E)
E) 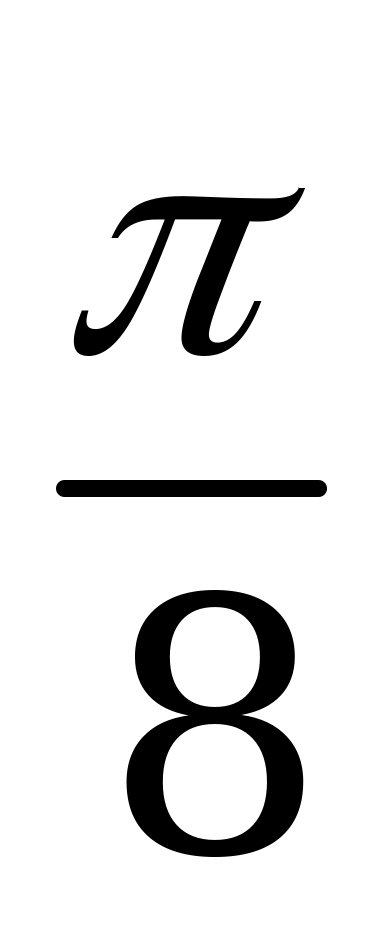
Найдите количество решений уравнения 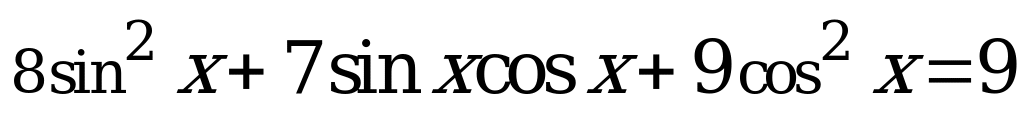 на интервале
на интервале 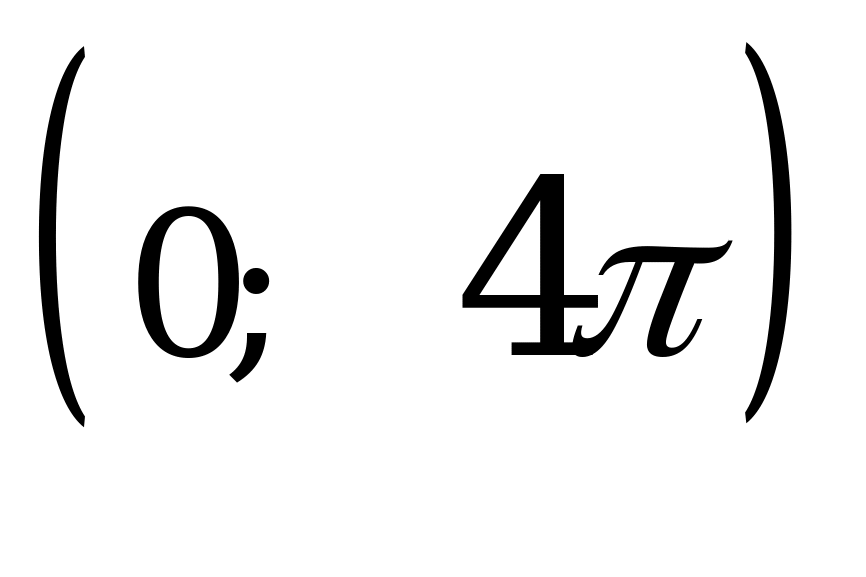
А) 3 B) 4 C) 7 D) 8 E) 9
Найдите количество решений уравнения 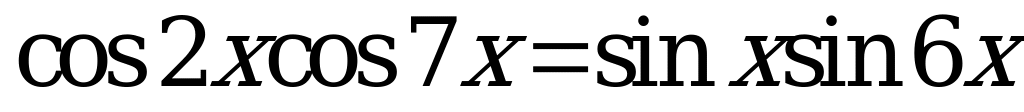 , принадлежащих интервалу
, принадлежащих интервалу 
А) 0 B) 7 C) 8 D) 9 E) 10
Сумма корней уравнения 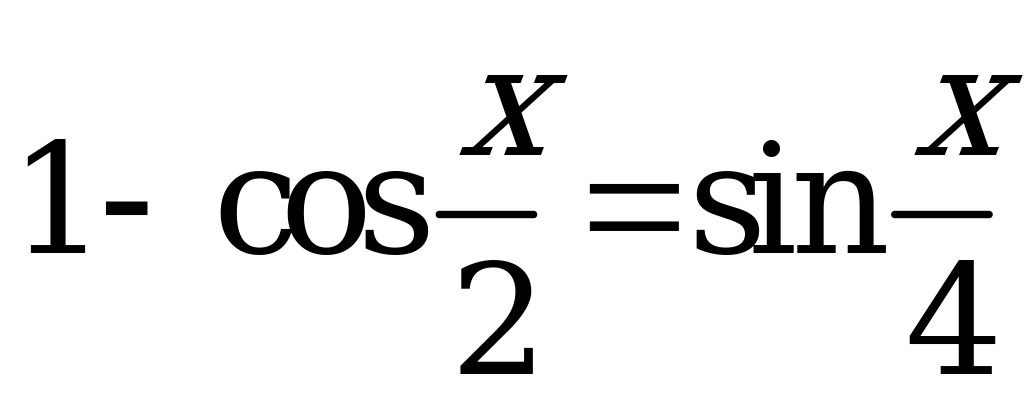 , принадлежащих промежутку
, принадлежащих промежутку 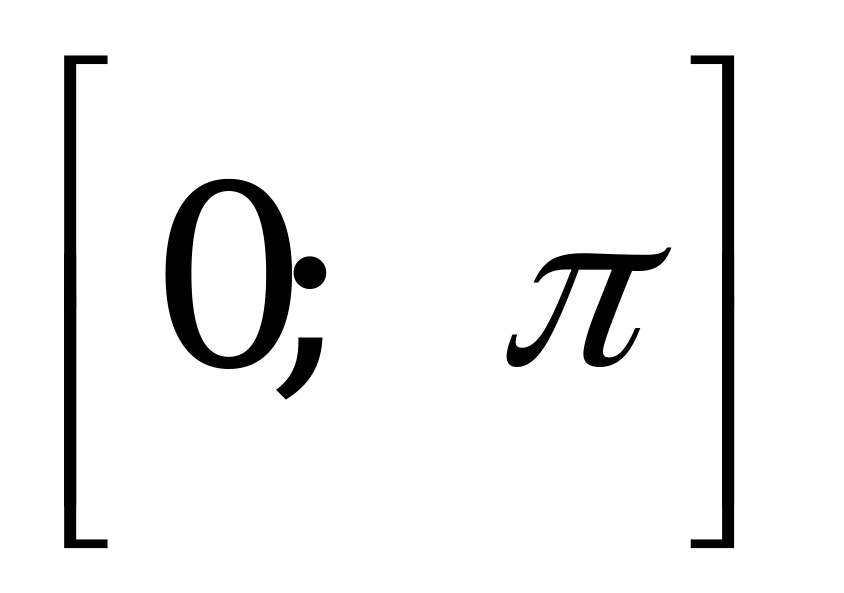 , равна числу
, равна числу
А) 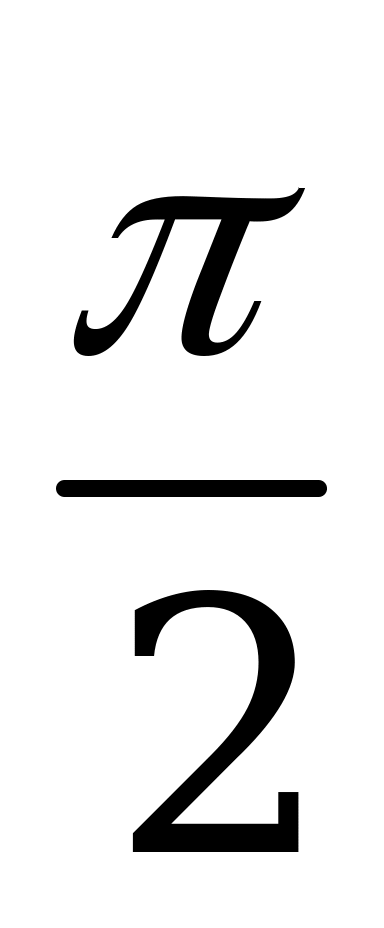 B)
B) 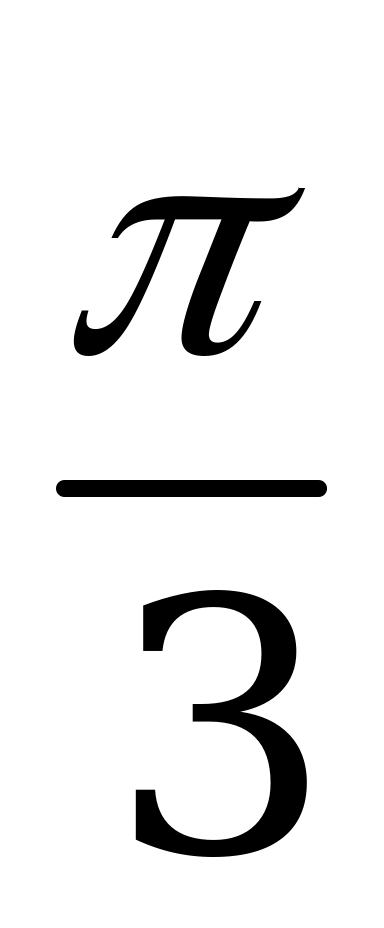 C)
C) 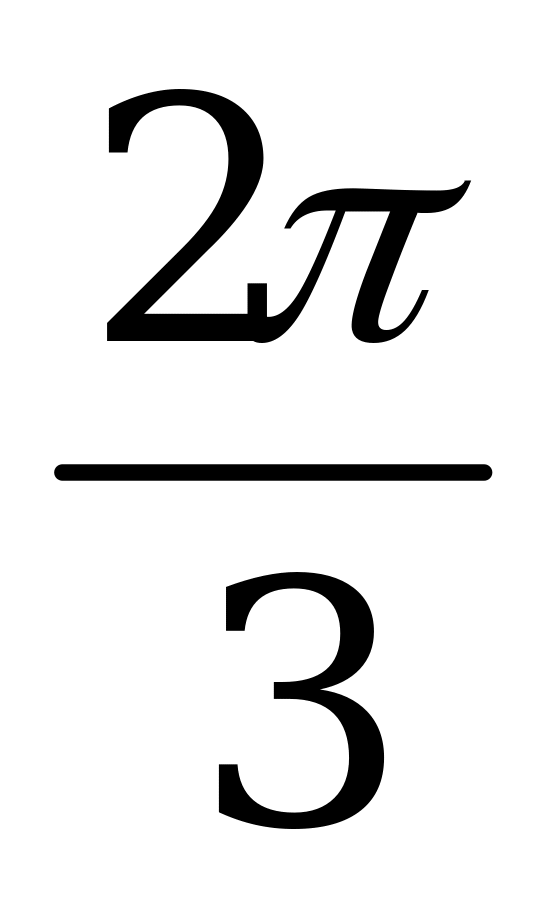 D)
D)  E)
E)
Число корней уравнения 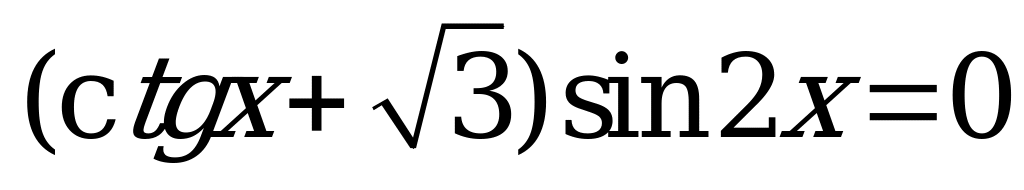 , лежащих в интервале
, лежащих в интервале 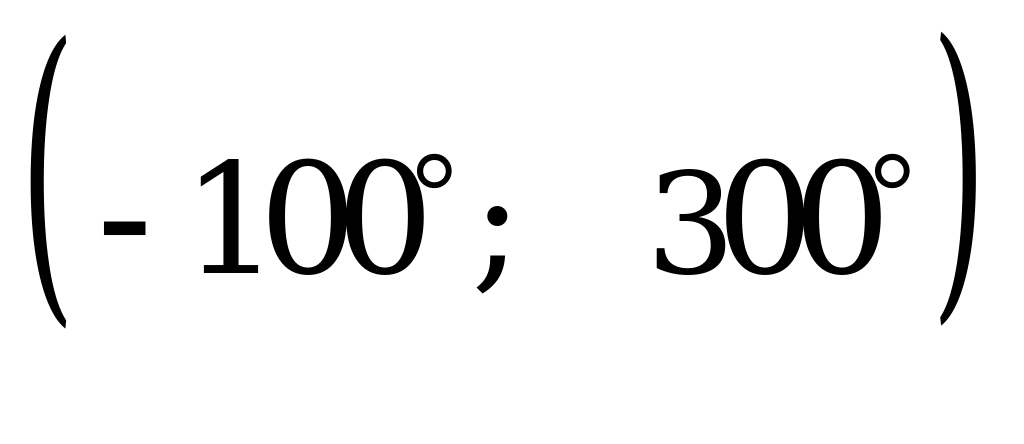 , равно
, равно
А) 3 B) 4 C) 5 D) 6 E) 7
Найдите в градусах среднее арифметическое всех различных корней уравнения 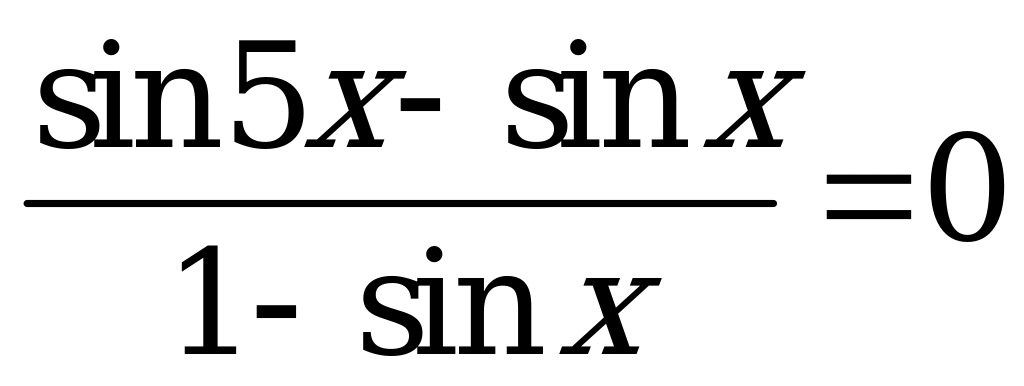 , принадлежащих промежутку
, принадлежащих промежутку 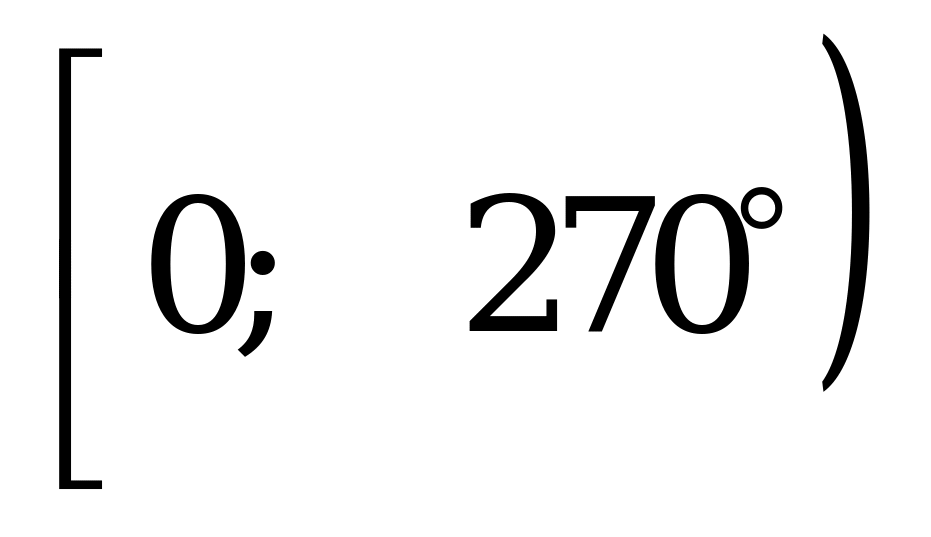 .
.
Найдите сумму (в градусах) двух самых больших корней уравнения 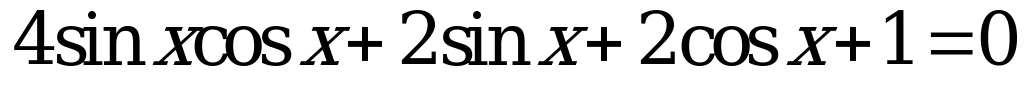 , принадлежащих промежутку
, принадлежащих промежутку 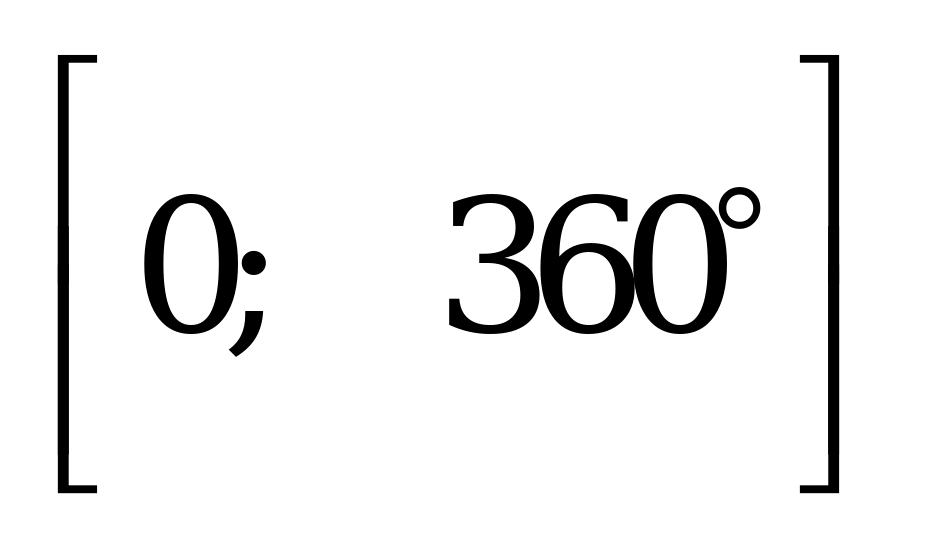
Укажите количество корней уравнения 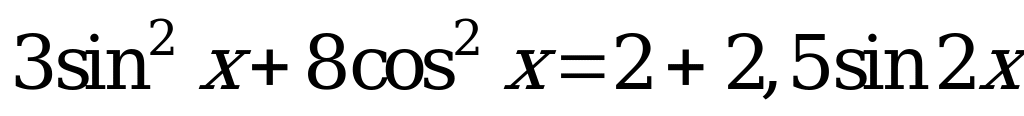 , принадлежащих отрезку
, принадлежащих отрезку 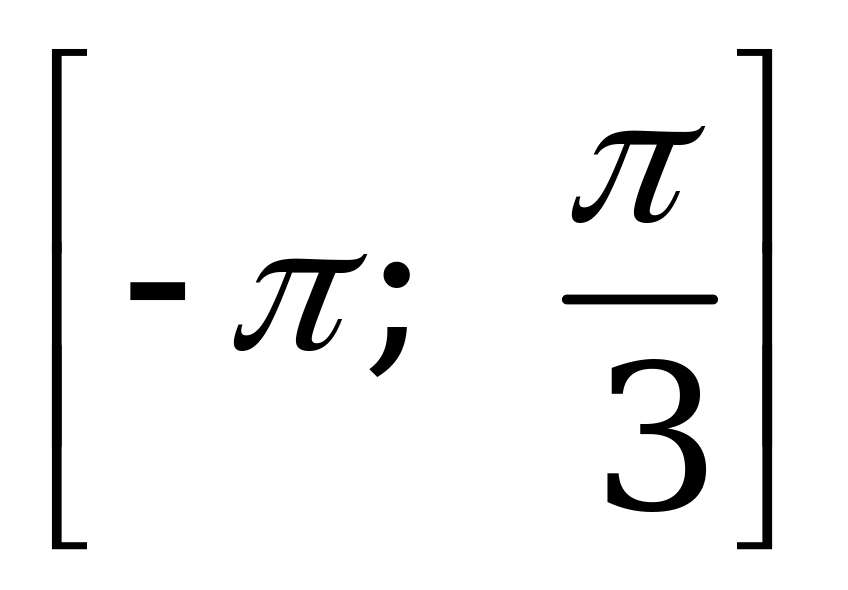 .
.
Найдите число решений уравнения  , принадлежащих отрезку
, принадлежащих отрезку 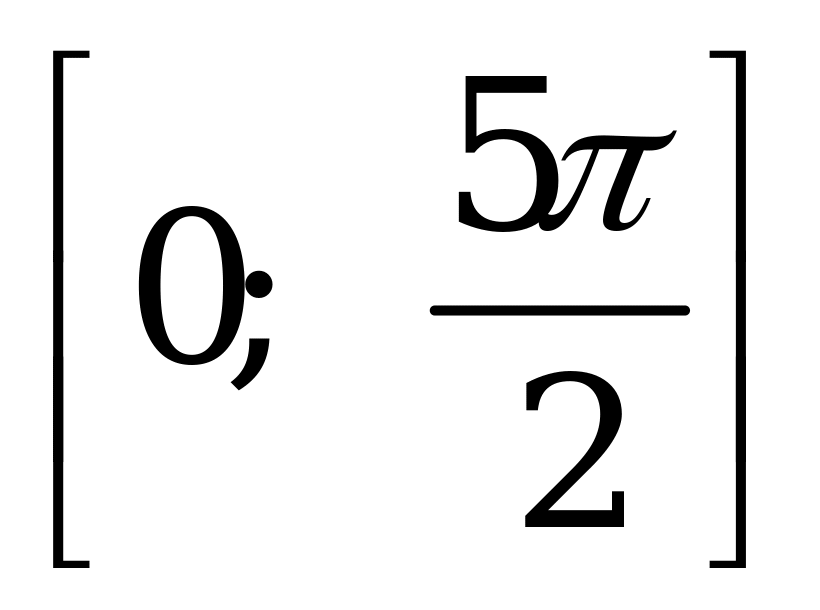
Найдите сумму корней уравнения 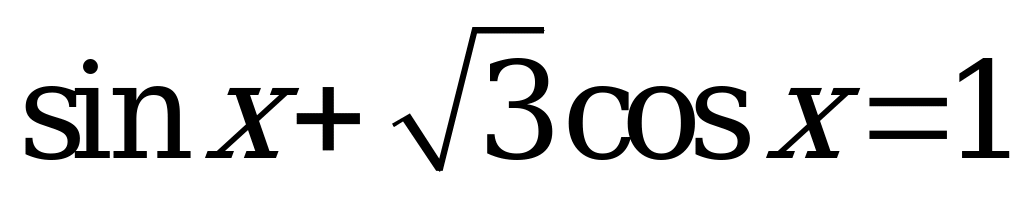 , принадлежащих интервалу
, принадлежащих интервалу 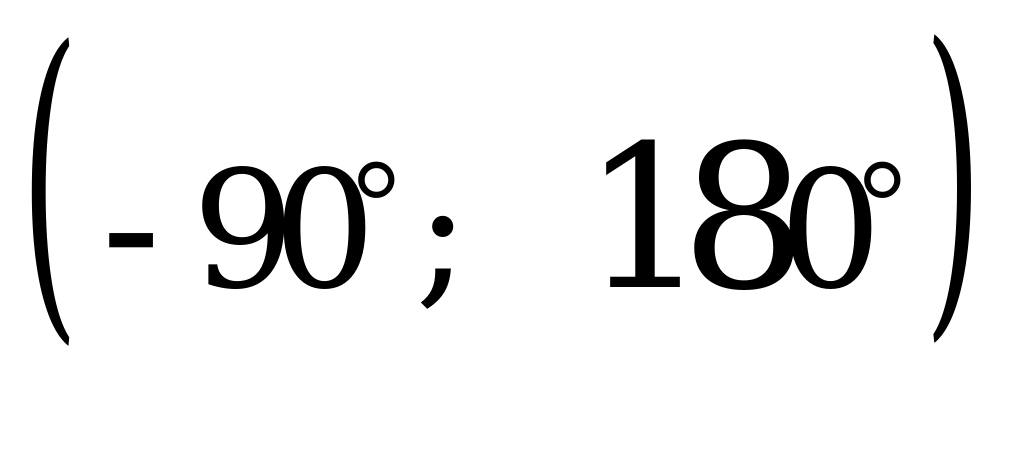
Укажите количество корней уравнения  , принадлежащих отрезку
, принадлежащих отрезку 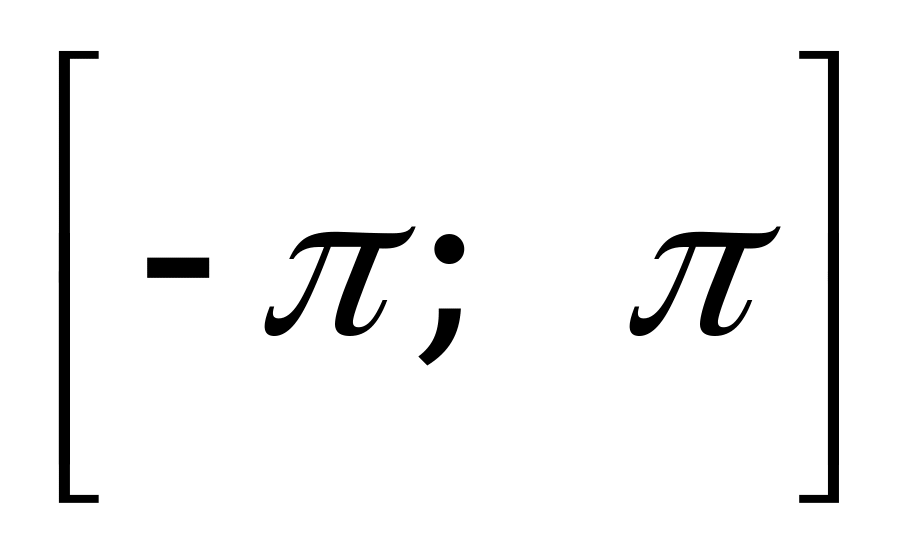 .
.
Укажите сумму корней (в градусах) уравнения 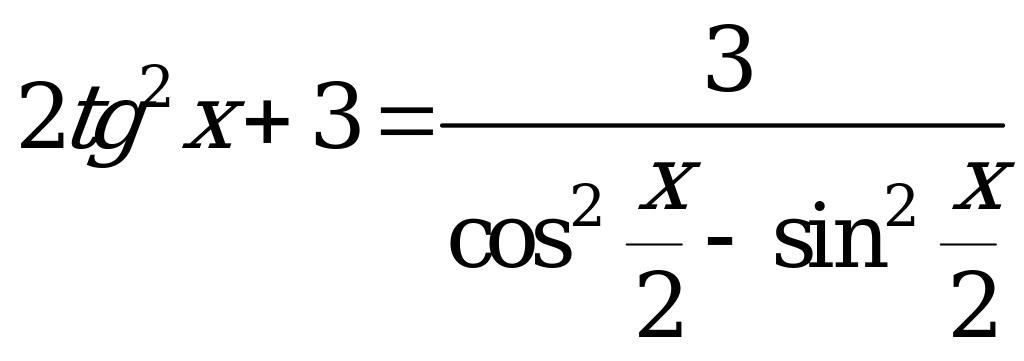 , принадлежащих отрезку
, принадлежащих отрезку 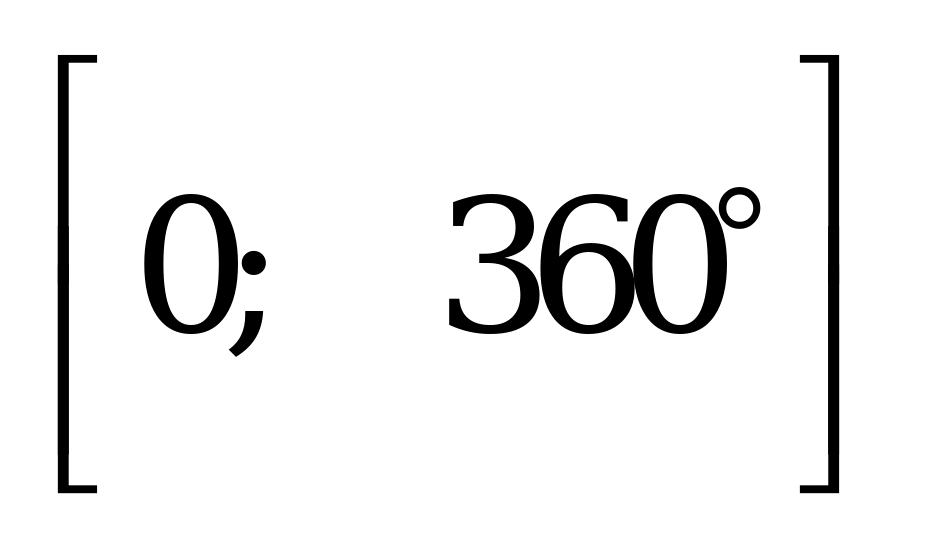 .
.
Найдите в градусах наименьший положительный корень уравнения 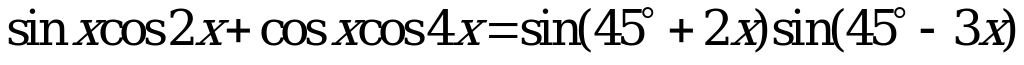 .
.
Укажите в градусах значение среднего арифметического всех корней уравнения 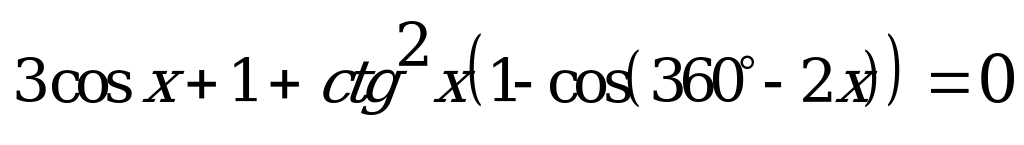 , принадлежащих промежутку
, принадлежащих промежутку 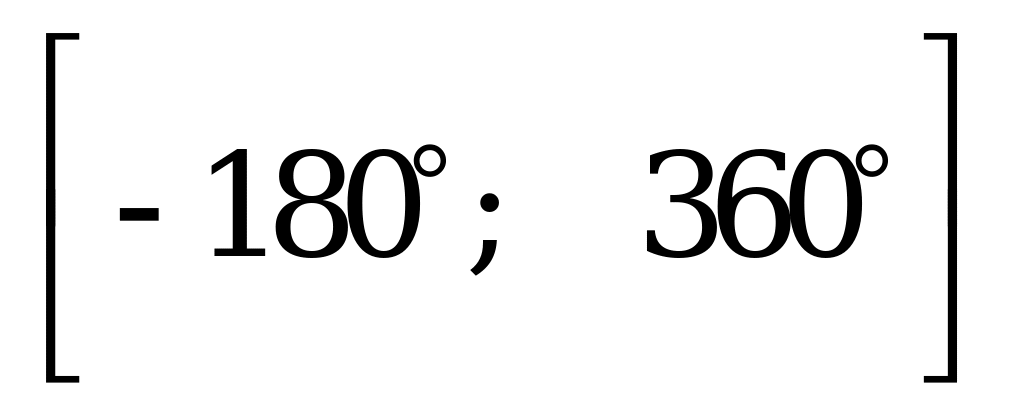 .
.
Найдите в градусах корень, если он единственный, или сумму корней уравнения 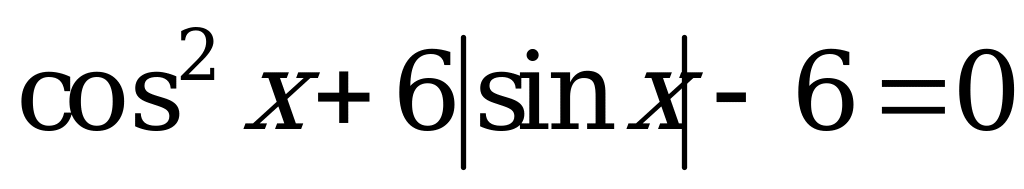 , принадлежащих промежутку
, принадлежащих промежутку 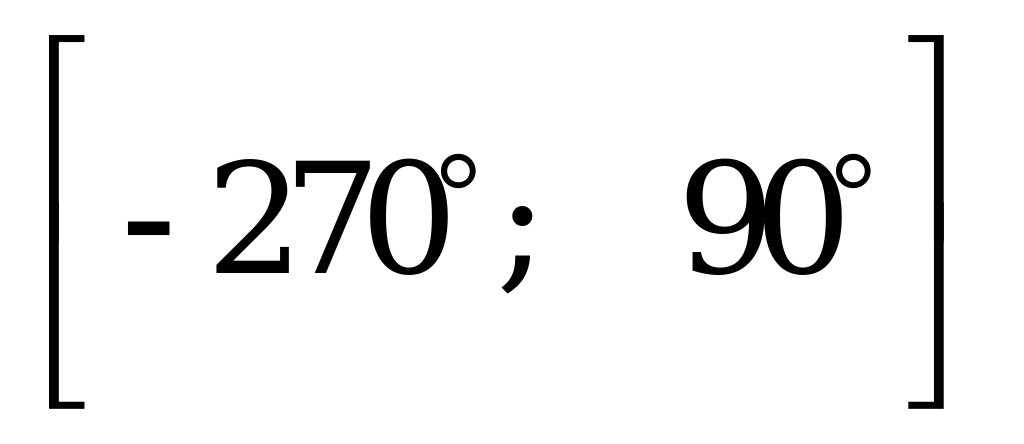 .
.
Решите уравнение 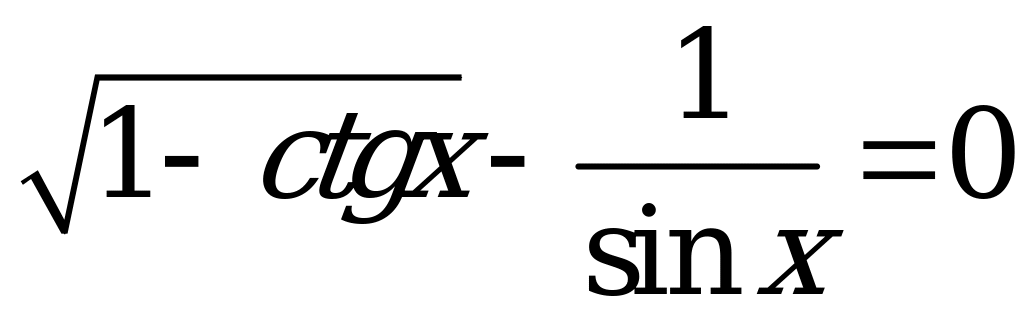 .
.
Решите уравнение 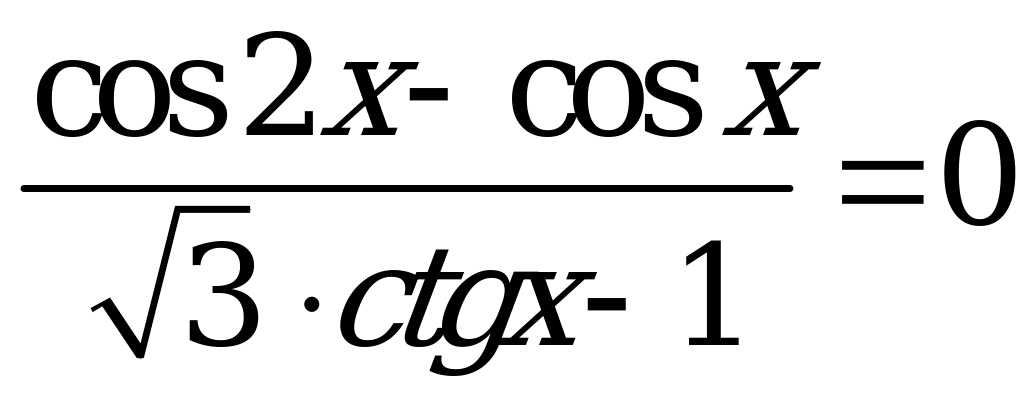 .
.
Решите уравнение 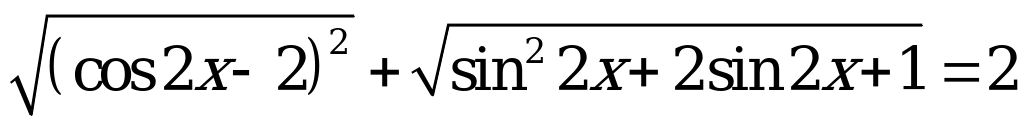 .
.
Ответы к обобщающему тесту
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| E | E | D | C | C | C | C | 114 | 570 | 2 | 6 | 60 | 2 | 360 | 45 | 80 |
Заключение
В данном проекте я изучил основные типы тригонометрических уравнений и методы их решения. Тригонометрические уравнения чаще всего встречаются в задаче 12 ЕГЭ. В большинстве случаев исходное уравнение в процессе решения сводится к простейшим тригонометрическим уравнениям. Однако для тригонометрических уравнений не существует единого метода решения. В каждом конкретном случае успех зависит от знания тригонометрических формул и от умения выбрать из них нужные. При этом обилие различных формул иногда делает этот выбор довольно трудным. В более сложных и нестандартных задачах нужно ещё догадаться, как использовать те или иные методы. Также потеря корней является распространенной грубой ошибкой. Другими такими ошибками являются неточное знание формул решений простейших тригонометрических уравнений, а также неумение правильно найти нужное значение аркфункции. Включение в ответ постороннего корня считается грубой ошибкой на ЕГЭ по математике.
В процессе работы над проектом мною составлены самостоятельные работы для подготовки к экзамену с ответами для самопроверки, собран материал о видах и способах тригонометрических задач. Разработан практикум по решению тригонометрических уравнений, содержащий задания различного уровня сложности, что позволит качественнее подготовиться к решению тригонометрических уравнений, встречающихся в контрольно-измерительных материалах ЕГЭ по математике профильного уровня.
Таким образом, в результате выполнения проекта поставленные цели достигнуты, задачи выполнены. Работая над проектом, я больше узнал об истории тригонометрии, типах и способах решения тригонометрических уравнений и, надеюсь, смогу успешно справиться с такими заданиями, которые могут встретиться мне на ЕГЭ.
СПИСОК ЛИТЕРАТУРЫ
Бородуля И.Т. Тригонометрические уравнения и неравенства: Книга для учителей/ Бородуля И.Т. – М.: Книга по требованию, 2013. [электронный вариант].
Мерзляк А.Г., Полонский В.Б., Рабинович Е.М., Якир М.С. Тригонометрия: Задачник к школьному курсу. – М.: АСТ-ПРЕСС: Магистр-S, 1998. [электронный вариант].
Шахмейстер А. Х. Тригонометрия. – 4-е издание. – М.: Издательство МЦНМО: СПб.: «Петроглиф»: «Виктория плюс», 2017. [электронный вариант].
Райхмистр Р. Б. Задачник по математике для учащихся средней школы и поступающих в вузы (с решениями и ответами). – М.: Московский Лицей, 2000. [электронный вариант].
Система тренировочных задач и упражнений по математике/ А.Я. Симонов, Д.С. Бакаев, А.Г. Эпельман и др. – М: Просвещение, 1991. [электронный вариант].
Лурье М. В. Тригонометрия. Техника решения задач: Учеб. пособие. – М.: Издательство УНЦ ДО, 2004. [электронный вариант].
Шабунин М. И. Математика: пособие для поступающих в вузы/ М.И. Шабунин. – 7-е изд., исправ. и доп. – М.: Лаборатория знаний, 2016.
Колесникова С. И. Методы решений тригонометрических уравнений. ЕГЭ. Математика/ С.И. Колесникова. – М.: ООО «Азбука-2000», 2017.
Гущин Д. Д. Сборник заданий по алгебре. Для подготовки к ЕГЭ и конкурсным экзаменам. – 10-е изд., перераб. и доп. – Париж, СПб: Стетоскоп, ВВМ, 2007.
Куланин Е. Д., Федин С. Н. 5000 конкурсных задач по математике. – М.: ООО «Фирма «Издательство АСТ», 1999.
3000 конкурсных задач по математике. – 5-е изд., исПример. – М.: Айрис-пресс, 2003.
В.С. Крамор, К.Н. Лунгу. Повторяем и систематизируем школьный курс тригонометрии: Пособие для старшеклассников и абитуриентов. – М.: АРКТИ, 2001.
Шестаков С.А., Захаров П.И. ЕГЭ 2019. Математика. Уравнения и системы уравнений. Задача 13 (профильный уровень) / Под ред. И.В. Ященко. – М.: МЦНМО, 2019. [электронный вариант].
Азаров А. И. и др. Тригонометрия. Тождества, уравнения, неравенства, системы: Учеб. пособие/ А.И. Азаров, В.И. Булатов, В.С. Федосеенко, А.С. Шибут/ – Мн.: «Полымя», 1998.
Потапов М. К. Задачи по алгебре, тригонометрии и элементарным функциям / М.К. Потапов. – М.: Издательство «Экзамен», 2008.
Данилов А. М. Математика. Тригонометрия и геометрия: Учебное пособие / А.М. Данилов, Т.В. Куликова, Т.А. Мишанина; Под общ. ред. д-ра техн. наук, проф. А.М. Данилова. – Пенза: ПГАСА, 2003.
Прокофьев А. А., Корянов А. Г. Математика. Подготовка к ЕГЭ. Тригонометрические уравнения: методы решения и отбор корней (типовые задания С1). – Изд. 2-е, доп. – Ростов-на-Дону: Легион, 2014.
Гельфанд И. М., Львовский С. М., Тоом А. Л. Тригонометрия. – 5-е изд., стереотип. - М.: МЦНМО, 2014. [электронный вариант].
Балаян Э. Н. Математика. ЕГЭ. Задачи типа С1 / Э.Н. Балаян. – Ростов н/Д: Феникс, 2013. [электронный вариант].
Крамор В.С., Михайлов П. А. Тригонометрические функции: (Система упражнений для самостоят. изучения). Пособие для учащихся. – 2-е изд., доп. – М: Просвещение, 1983.
А.И. Худобин, И.И. Худобин. Сборник задач по тригонометрии. Пособие для учителей. Изд. 2-е. – М.: Государственное учебно-педагогическое издательство Министерства просвещения РСФСР, 1955.
Просветов Г. И. Тригонометрия: задачи и решения: Учебно-практическое пособие. – М.: Издательство «Альфа-Пресс», 2010.
Севрюков П.Ф. Тригонометрические, показательные и логарифмические уравнения и неравенства: учебное пособие / П.Ф. Севрюков, А.Н. Смоляков. – М: Илекса; Народное образование; Ставрополь: Сервисшкола, 2008. [электронный вариант].
Использованные интернет-источники:
1. https://youclever.org/book/trigonometricheskie-uravneniya-1/
2. https://ege-study.ru/ru/ege/materialy/matematika/trigonometricheskie-uravneniya/
3. http://cos-cos.ru/math/93/
4.https://www.yaklass.ru/p/algebra/10-klass/trigonometricheskie-uravneniia-9145/metody-ispolzuemye-dlia-resheniia-trigonometricheskikh-uravnenii-9134/re-995e0a3e-90bc-4e3a-b784-3f48ab285dde
5. https://www.resolventa.ru/index.php/trigonometricheskie-uravnenija
6. https://resh.edu.ru/subject/lesson/6320/conspect/200019/
7. https://dl.bsu.by/mod/book/view.php?id=10177&chapterid=1270
8. https://shkolkovo.net/catalog/reshenie_uravnenij_2/trigonometricheskie
9. https://mat.1sept.ru/view_article.php?ID=200301001
10. http://egesdam.ru/page310.php
11. http://egesdam.ru/page311.php
Приложение
Практикум по теме «Решение тригонометрических уравнений»




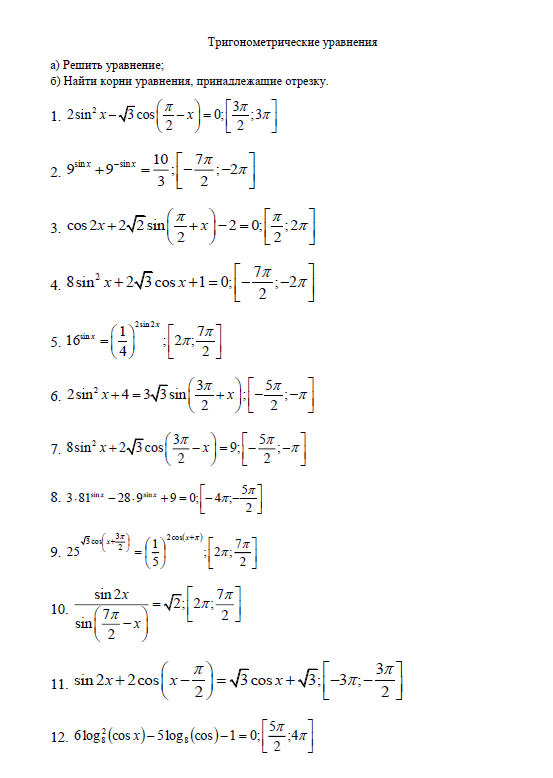








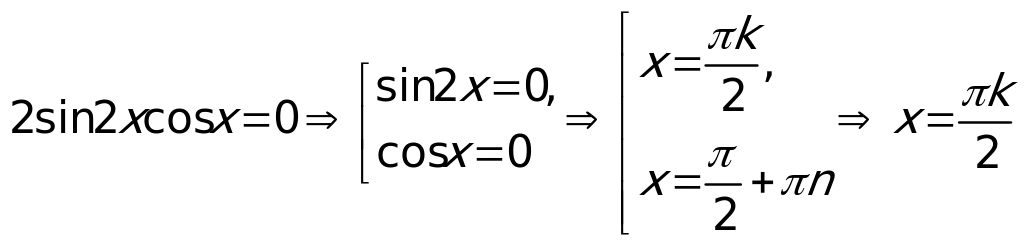 Ответ:
Ответ: 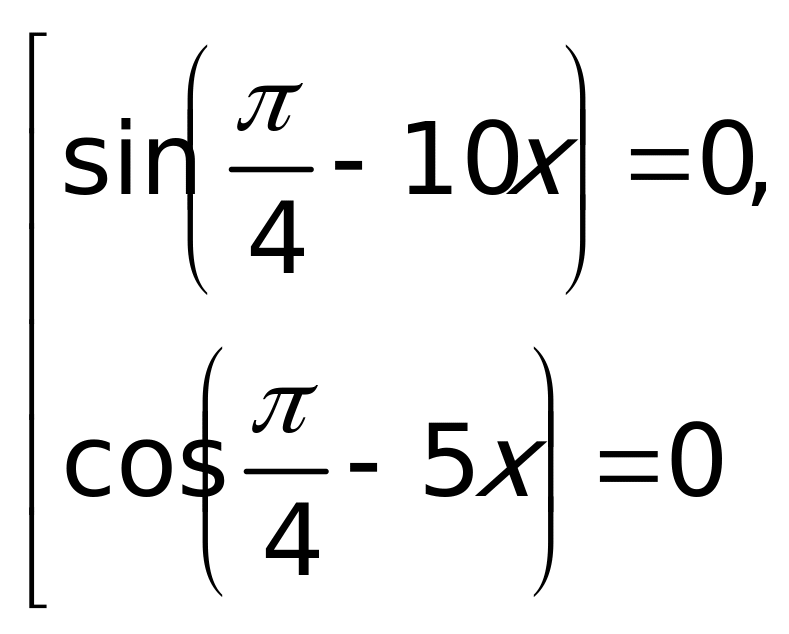
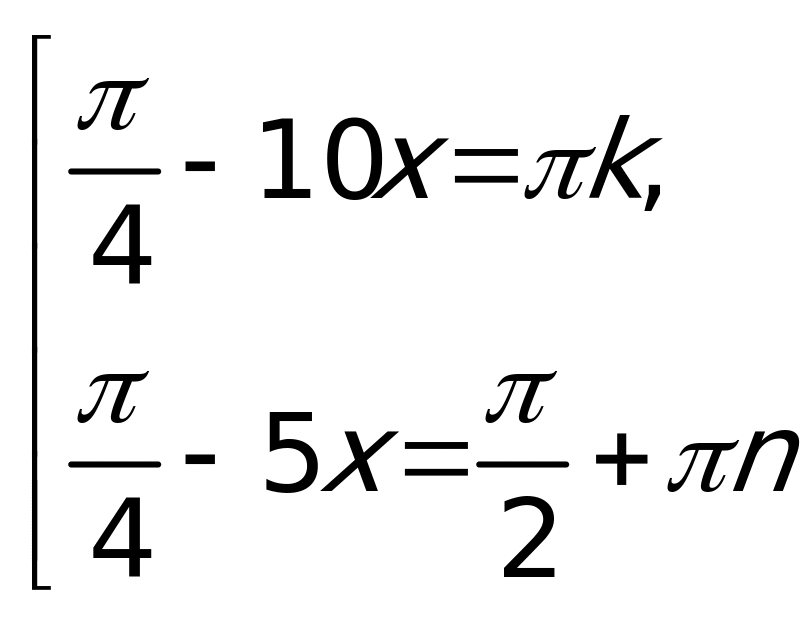
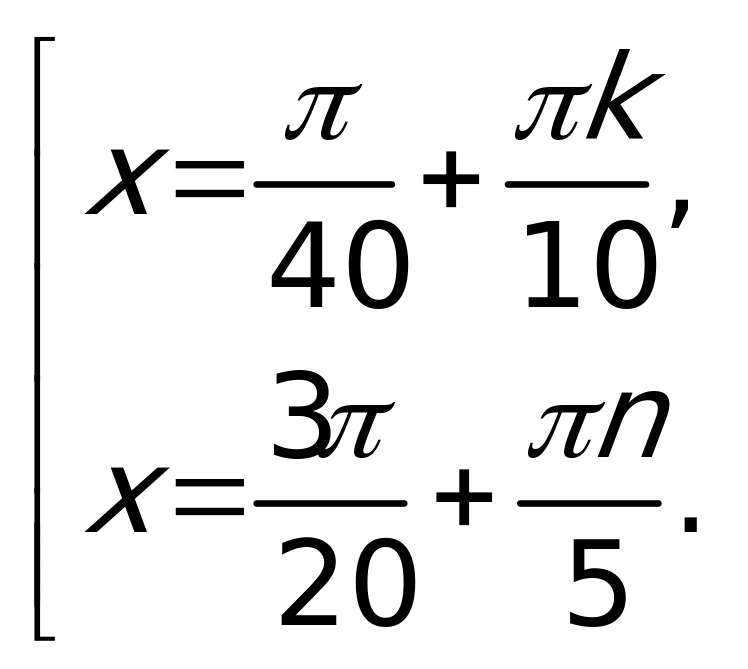
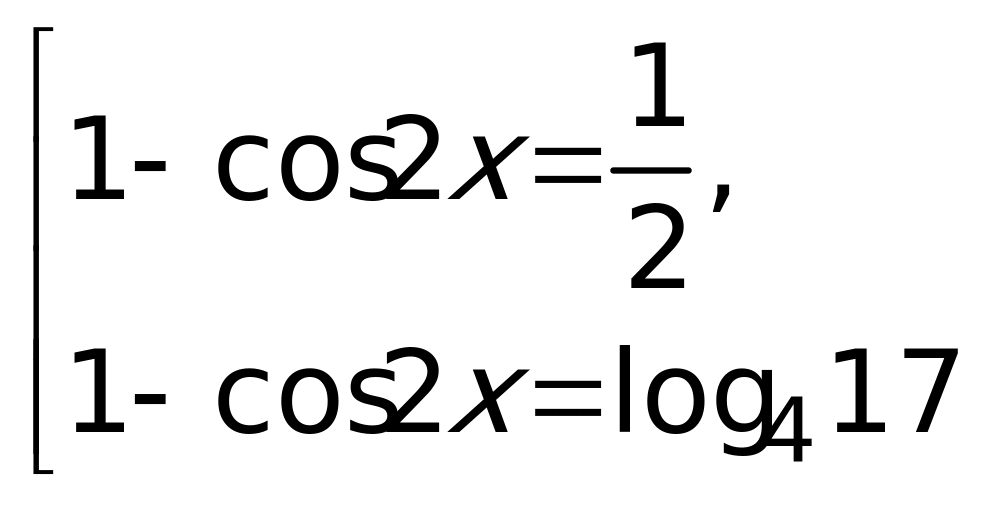
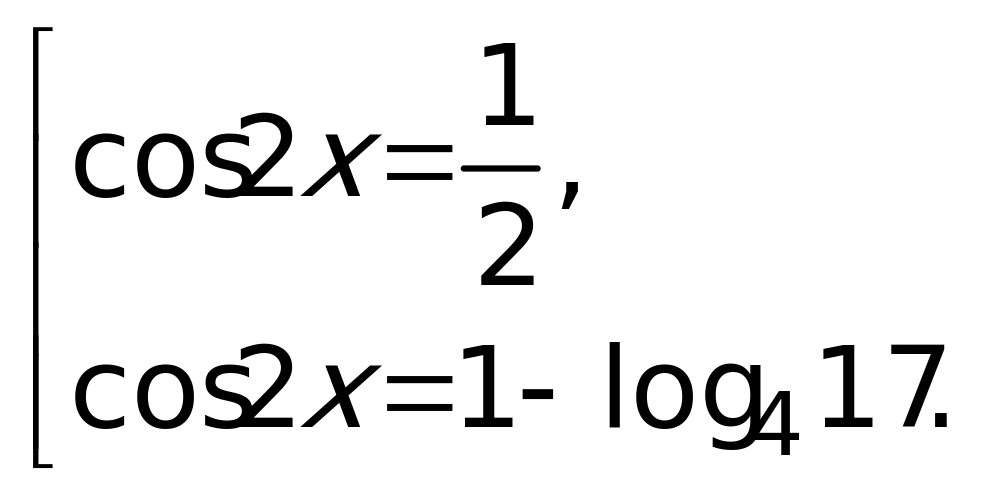
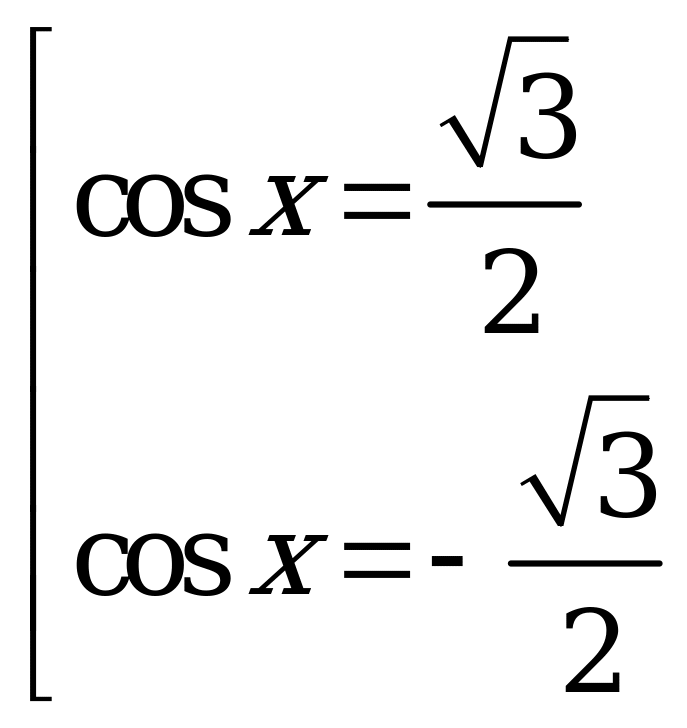 , решением которой является множество
, решением которой является множество 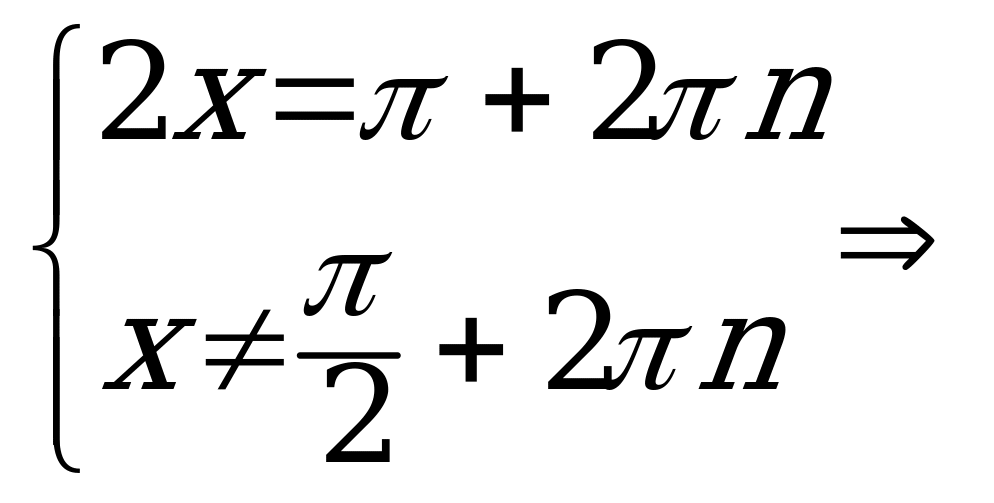
 , принадлежащих отрезку
, принадлежащих отрезку