Муниципальное бюджетное общеобразовательное учреждение
«Школа № 46» города Рязани
"Загадка чисел Фибоначчи".
Работу выполнили:
ученики 6 класса «Б»
Козловский Михаил и
Чудакова Виктория
Рязань
Оглавление
Введение………………………………………………………………………3
Глава 1. Уникальная числовая последовательность Фибоначчи ……….5
Глава 2. Числа Фибоначчи вокруг и внутри нас ..……………………… 7
Глава 3. Практическая часть………………………………………………17
Глава 4. Заключение………………………………………………..……….23
Список используемой литературы и сайтов Интернета……………….…..24
Введение
Феномен - (от греч. phainomenon - являющееся) необычный, исключительный факт, явление...
Энциклопедический словарь.
Древняя история богата выдающимися математиками. Многие достижения древней математической науки до сих пор вызывают восхищение остротой ума их авторов, а имена Евклида, Архимеда, Герона известны каждому образованному человеку. Иначе обстоит дело с математикой средневековья. Математика в эту эпоху развивалась чрезвычайно медленно, и крупных математиков тогда было очень мало. Тем больший интерес представляет для нас сочинение “Liber abacci” (“Книга об абаке”), написанная знаменитым итальянским математиком Леонардо из Пизы (ок. 1170-после 1228), более известный под прозвищем Фибоначчи, который был, безусловно, самым значительным математиком средневековья.
Мы обратились к современному источнику информации – к Интернету и прочитали о числах Фибоначчи, о магических числах, которые таят в себе великую загадку. Оказывается, эти числа можно найти в подсолнухах и сосновых шишках, в крыльях стрекозы и морских звёздах, в ритмах человеческого сердца и в музыкальных ритмах...
Почему же эта последовательность чисел столь распространена в нашем мире?
Удивительная математическая игрушка оказалась уникальным кодом, заложенным во все природные объекты самим Творцом Вселенной. Изучить этот код, как феномен нам стало также интересно, как и всем великим математикам.
Цель исследовательской работы – изучение проявления чисел Фибоначчи, связанного с ним закона золотого сечения в строении живых и неживых объектов, найти примеры использования чисел Фибоначчи в современном мире и доказать их феноменальность.
Задачи:
Познакомиться и изучить материал теории чисел Фибоначчи.
Описать способ построения ряда Фибоначчи и спирали Фибоначчи.
Найти примеры последовательности чисел Фибоначчи и Золотого сечения в строении живых и неживых объектов.
Увидеть математические закономерности, в строении человека, растительного мира и неживой природы с точки зрения феномена Золотого сечения.
Провести практическую работу по изучению человеческой кисти учеников 6-го класса на соответствие теории чисел Фибоначчи.
Провести исследование присутствия золотого сечения в стихотворениях.
Провести исследование присутствия золотого сечения в живописи.
Провести исследование присутствия золотого сечения на плакатах с рекламой.
Методы исследования:
эмпирический (наблюдение, эксперимент, измерение).
теоретический (логическая ступень познания).
Гипотеза:
Г лава 1. Уникальная числовая последовательность Фибоначчи
лава 1. Уникальная числовая последовательность Фибоначчи
Удивительные числа были открыты итальянским математиком средневековья Леонардо Пизанским, более известным под именем Фибоначчи. Путешествуя по Востоку, он познакомился с достижениями арабской математики, способствовал передаче их на Запад. В одном из своих трудов под названием «Книга вычислений» он представил Европе одно из величайших открытий всех времён и народов – десятичную систему счисления.
Однажды, он ломал голову над решением одной математической задачи. Он пытался создать формулу, описывающую последовательность размножения кроликов.
«Сколько пар кроликов в один год от одной пары родится». Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:
| Месяцы | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | и.т.д. |
| Пары кроликов | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | и.т.д |
Разгадкой стал числовой ряд, каждое последующее число которого, является суммой двух предыдущих:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, ...
Числа, образующие данную последовательность называются "числами Фибоначчи", а сама последовательность - последовательностью Фибоначчи.
«Ну и что?» - скажете вы, - «Мали ли мы сами можем придумать подобных числовых рядов, нарастающих по заданной прогрессии?» Действительно, когда появился ряд Фибоначчи, никто, в том числе и он сам, не подозревал, насколько близко ему удалось приблизиться к разгадке одной из величайших тайн мироздания!
Фибоначчи вёл отшельнический образ жизни, много времени проводил на природе, и, гуляя в лесу, он обратил внимание, что эти числа стали буквально преследовать его. Повсюду в природе он снова и снова встречал эти числа. Например, лепестки и листья растений строго укладывались в данный числовой ряд.
В числах Фибоначчи существует интересная особенность: частное от деления последующего числа Фибоначчи на предыдущее, по мере роста самих чисел, стремиться к 1,618. Именно это постоянное число деления в средние века было названо Божественной пропорцией, а ныне именуется как золотое сечение или золотая пропорция.
В алгебpе это число обозначается гpеческой буквой фи (Ф)
Итак, φ = 1,618
233 / 144 = 1,618
377 / 233 = 1,618
610 / 377 = 1,618
987 / 610 = 1,618
1597 / 987 = 1,618
2584 / 1597 = 1,618
Сколько бы раз мы не делили одно на другое, соседнее с ним число, мы всегда получим 1, 618. А если сделаем наоборот, то есть разделим меньшее число на большее, то получим 0, 618, это число, обратное к 1, 618, тоже называется золотой пропорцией.
Ряд Фибоначчи мог бы остаться только математическим казусом, если бы не то обстоятельство, что все исследователи золотого деления в растительном и в животном мире, не говоря уже об искусстве, неизменно приходили к этому ряду, как арифметическому выражению закона золотого деления.
Учёные, анализируя дальнейшее применение этого числового ряда к природным феноменам и процессам, обнаружили, что эти числа содержатся буквально во всех объектах живой природы, в растениях, в животных и в человеке.
Удивительная математическая игрушка оказалась уникальным кодом, заложенным во все природные объекты самим Творцом Вселенной.
Глава 2. Числа Фибоначчи вокруг и внутри нас.
Золотое сечение и числа Фибоначчи природе.
Если посмотреть на растения и деревья вокруг нас, то видно, сколь много листьев на каждом из них. Издалека кажется, что ветки и листья на растениях расположены случайным образом, в произвольном порядке. Однако во всех растениях чудесным образом, математически точно спланировано какая веточка откуда будет произрастать, как ветки и листья будут располагаться около стебля или ствола. С первого дня появления растение в точности следует в своём развитии этим законам, то есть ни один лист, ни один цветок не появляется случайно. Ещё до появления растение уже точно запрограммировано. Сколько будет веток на будущем дереве, где вырастут ветки, сколько будет листьев на каждой ветке, и как, в каком порядке будут располагаться листья. Совместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке (филотаксис), в числе оборотов на стебле, в числе листьев в цикле проявляет себя ряд Фибоначчи, а стало быть, проявляет себя и закон золотого сечения.
Если вы зададитесь целью отыскать числовые закономерности в живой природе, то заметите, что эти числа часто встречаются в различных спиральных формах, которыми так богат мир растений. Например, черенки листьев примыкают к стеблю по спирали, которая проходит между двумя соседними листьями: 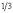 полного оборота - у орешника,
полного оборота - у орешника, 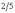 - у дуба,
- у дуба, 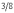 - у тополя и груши,
- у тополя и груши,  - у ивы.
- у ивы.
Семена подсолнечника, эхинацеи пурпурной и многих других растений, расположены спиралями, причем количества спиралей каждого направления - числа Фибоначчи.


Подсолнечник, 21 и 34 спирали. Эхинацея, 34 и 55 спиралей.
Чёткая, симметричная форма цветов также подчинена строгому закону.
У многих цветов количество лепесточков – именно числа из ряда Фибоначчи. Например:




ирис, 3леп. лютик, 5 леп. златоцвет, 8 леп. дельфиниум,
13 леп.



цикорий,21леп. астра, 34 леп. маргаритки,55леп.
Ряд Фибоначчи характеризует структурную организацию многих живых систем.
Громкость звука.
Известно, что максимальная громкость звука, которая вызывает болевые ощущения, равна 130 децибелам. Если разделить этот интервал золотой пропорцией 1,618, то получим 80 децибел, которые характерны для громкости человеческого крика. Если теперь 80 децибел разделить золотой пропорцией, то получим 50 децибел, что соответствует громкости человеческой речи.
Золотое сечение в строении тела человека
Если принять центром человеческого тела точку пупа, а расстояние между ступней человека и точкой пупа за единицу измерения, то рост человека эквивалентен числу 1.618
Рука человека
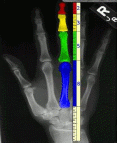
Достаточно лишь приблизить сейчас вашу ладонь к себе и внимательно посмотреть на указательный палец, и вы сразу же найдете в нем формулу золотого сечения. Каждый палец нашей руки состоит из трех фаланг.
Сумма двух первых фаланг пальца в соотношении со всей длиной пальца и дает число золотого сечения (за исключением большого пальца).
Кроме того, соотношение между средним пальцем и мизинцем также равно числу золотого сечения.
У человека 2 руки, пальцы на каждой руке состоят из 3 фаланг (за исключением большого пальца). На каждой руке имеется по 5 пальцев, то есть всего 10, но за исключением двух двухфаланговых больших пальцев только 8 пальцев создано по принципу золотого сечения. Тогда как все эти цифры 2, 3, 5 и 8 есть числа последовательности Фибоначчи.
Золотые пропорции в строении молекулы ДНК.
Все сведения о физиологических особенностях живых существ, будь то растение, животное или человек, хранятся в микроскопической молекуле ДНК, строение которой также содержит в себе закон золотой пропорции. Молекула ДНК состоит из двух вертикально переплетенных между собой спиралей. Длина каждой из этих спиралей составляет 34 ангстрема, ширина 21 ангстрема. (1 ангстрем - одна стомиллионная доля сантиметра).

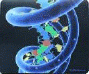

Так вот 21 и 34 - это цифры, следующие друг за другом в последовательности чисел Фибоначчи, то есть соотношение длины и ширины логарифмической спирали молекулы ДНК несет в себе формулу золотого сечения 1:1,618.
Не только прямоходящие, но и все плавающие, ползающие, летающие и прыгающие не избежали участи подчиняться числу фи. Сердечная мышца человека сокращается до 0, 618 своего объёма. Строение ракушки улитки соответствует пропорциям Фибоначчи. И таких примеров можно найти предостаточно – было бы желание исследовать природные объекты и процессы. Мир настолько пронизан числами Фибоначчи, что порой кажется: только ими Вселенная и может быть объяснена.
Спираль Фибоначчи.
В математике нет иной формы, которая обладала бы такими же уникальными свойствами, как спираль, потому, что
в основе строения спирали лежит правило Золотого сечения!
Чтобы понять математическое построение спирали, повторим, что такое Золотое сечение.
Золотое сечение - это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей, или, другими словами, меньший отрезок так относится к большему, как больший ко всему.
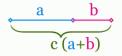
То есть (a+b) /a = a / b
Прямоугольник с именно таким отношением сторон стали называть золотым прямоугольником. Его длинные стороны соотносятся с короткими сторонами в соотношении 1,168 : 1.
Золотой прямоугольник обладает многими необычными свойствами. Отрезав от золотого прямоугольника квадрат, сторона которого равна меньшей стороне прямоугольника,
мы снова получим золотой прямоугольник меньших размеров.
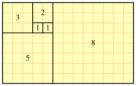
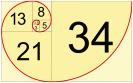
Этот процесс можно продолжать до бесконечности. Продолжая отрезать квадраты, мы будем получать все меньшие и меньшие золотые прямоугольники. Причем располагаться они будут по логарифмической спирали, имеющей важное значение в математических моделях природных объектов.
Например, спиралевидную форму можно увидеть и в расположении семян подсолнечника, в ананасах, кактусах, строении лепестков роз и так далее.


Нас удивляет и восхищает спиральное строение ракушек.



У большинства улиток, которые обладают раковинами, раковина растет в форме спирали. Однако нет сомнения, что эти неразумные существа не имеют представления не только о спирали, но не обладают даже простейшими математическими знаниями, чтобы самим создать себе спиралевидную раковину.
Но тогда как же эти неразумные существа смогли определить и избрать для себя идеальную форму роста и существования в виде спиральной раковины? Могли ли эти живые существа, которых ученых мир называет примитивными формами жизни, рассчитать, что идеальной для их существования будет спиральная форма ракушки?
Пытаться объяснить происхождение подобной даже самой примитивной формы жизни случайным стечением неких природных обстоятельств по меньшей мере абсурдно. Совершенно ясно, что этот проект является осознанным творением.
Спирали есть и в человеке. С помощью спиралей мы слышим:

Спирали есть на наших ладошках и пальцах:
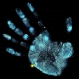
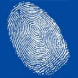
В животном мире мы также можем найти множество примеров спиралей.
В форме спирали развиваются рога и бивни животных, когти львов и клювы попугаев являют собой логарифмические формы и напоминают форму оси, склонной обратиться в спираль.



Интересно, что спиралью закручивается ураган, облака циклона и это хорошо видно из космоса:


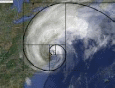
В океанских и морских волнах спираль можно математически отразить на графике с точками 1,1,2,3,5,8,13,21,34 и 55.

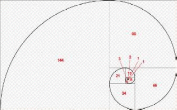
Такую «бытовую» и «прозаическую» спираль тоже все узнают.
Ведь вода убегает из ванной по спирали:

Да и живём мы с вами в спирали, ведь галактика – это спираль, соответствующая формуле Золотого сечения!

Итак, мы выяснили, что если взять Золотой прямоугольник и разбить его на более мелкие прямоугольники в точной последовательности Фибоначчи, а потом каждый из них разделить в таких пропорциях еще и еще, то получится система, которая называется спираль Фибоначчи.
Эту спираль мы обнаружили в самых неожиданных предметах и явлениях. Теперь понятно, почему спираль называют ещё «кривой жизни».
Спираль стала символом эволюции, ведь и развивается всё именно по спирали.
Золотое сечение в живописи.
Золотое сечение в живописи. Еще в эпоху Возрождения художники открыли, что любая картина имеет определенные точки, невольно приковывающие наше внимание, так называемые зрительные центры. При этом абсолютно неважно, какой формат имеет картина - горизонтальный или вертикальный. Таких точек всего четыре, они делят величину изображения по горизонтали и вертикали в золотом сечении, т.е. расположены они на расстоянии примерно 3/8 и 5/8 от соответствующих краев плоскости.
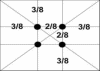
Данное открытие у художников того времени получило название "золотое сечение" картины. Поэтому, для того чтобы привлечь внимание к главному элементу фотографии, необходимо совместить этот элемент с одним из зрительных центров.
Картина Н.Н. Ге "Александр Сергеевич Пушкин в селе Михайловском".

В этой картине фигура Пушкина поставлена художником слева на линии золотого сечения. Композиционное построение картины подобно картине Репина. Голова военного, с восторгом слушающего чтение поэта, находится на другой вертикальной линии золотого сечения.
Золотое сечение в поэзии.
Примеры из поэзии бесчисленны. Особенно ими изобилует А. С. Пушкин.
Так например, основная схема построения “Евгения Онегина” основана на близости к трём числам Фибоначчи: 8, 13, 55.
Практически во всех его произведения присутствует золотое сечении.
Глава 3. Практическая часть
3.1. Исследование человека
После проведенных исследований нам стало интересно то, что почти весь человек создан по примеру чисел Фибоначчи и золотого сечения. И мы решили, проверить это на наших одноклассниках. И вот что у нас получилось:
|
| 2 фаланга / 1 фаланга = | 3 фаланга / 2 фаланга = | 4 фаланга / 3 фаланга = | расстояние от запястья до локтя / от кончиков пальцев до запястья |
| Полина Ч. | 29.1/18=1.617 | 48/29.1=1.649 | 79/48=1.645 | 25.8/16=1.613 |
| Оля | 31,7/19,4=1,634 | 51.1/31,7=1,612 | 82,2/51.1=1,608 | 29,7/17,9=1,659 |
| Юля Я. | 30.4/18.8=1,617 | 48.7/30.4=1,602 | 79,4/48.7=1,630 | 26,4/16,6=1,590 |
| Катя Г. | 30.6/19=1.611 | 49.4/30.6=1.614 | 80/49.4=1.619 | 24/15.1=1.589 |
| Катя З. | 31/19,2=1,615 | 50,1/31=1,616 | 80,1/50,1=1,599 | 29/18=1,611 |
| Наташа | 29.6/18.7=1,583 | 48/29.6=1,622 | 78,9/48=1,643 | 27,2/17=1,600 |
| Саша | 31,9/19.8=1,611 | 51/31,9=1,599 | 82,1/51=1,610 | 29/18=1,611 |
| Катя С. | 32.1/20=1.605 | 52.2/32.1=1.626 | 84/52.2=1.609 | 28.5/18=1.583 |
| Маша Кл. | 34/21=1,619 | 55/34=1,618 | 89/55=1,618 | 30,1/18=1,672 |
| Маша Кон. | 31,3/20,1=1,557 | 50.3/31,3=1,607 | 81,1/50.3=1,612 | 32/19=1,684 |
| Настя Н. | 31.4/19,5=1,610 | 49/30=1,633 | 80,1/49=1,635 | 26,5/16,9=1,568 |
| Настя А. | 31/18,6=1,667 | 50/31=1,613 | 80,7/50=1,614 | 27,5/17=1,618 |
| Полина Х. | 32/21=1,667 | 51,8/32=1,619 | 83,4/51,8=1,610 | 29,2/17,8=1,640 |
| Алеша | 34/21=1,619 | 55/34=1,617 | 89/55=1,618 | 30/18,6=1,613 |
| Вася | 35/21,5=1,628 | 55,5/35=1,586 | 90,4/55,5=1,629 | 30,6/19=1,610 |
| Родион | 34,9/21,6=1,582 | 56,8/34,9=1,627 | 90,3/56,8=1,600 | 30,6/19=1,610 |
| Юра | 29/18=1,611 | 48/29=1,655 | 79,2/48=1,650 | 27/16,7=1,617 |
| Максим | 31/19,5=1,600 | 50/31=1,613 | 80/50=1,600 | 26,1/16,1=1,621 |
| Коля | 31/18,6=1,667 | 49,5/31=1,597 | 82/49,5=1,656 | 27,3/17=1,606 |
| Артем | 30.8/18.9=1,629 | 49.8/30.8=1,617 | 80/49.8=1,606 | 27,2/16,9=1,609 |
| Егор | 31/19=1,631 | 50/31=1,613 | 80/50=1,600 | 30,4/18,7=1,626 |
| Антон | 35,6/22,1=1,611 | 57/35,6=1,601 | 90,3/57=1,584 | 30,9/19,2=1,609 |
| Рома | 29/18=1,611 | 48/29=1,655 | 80/50=1,600 | 29/18=1,611 |
| Ср.ариф. девоч. | 1,616 | 1,618 | 1,619 | 1,618 |
| Ср.ариф. мал. | 1,619 | 1,618 | 1,614 | 1,613 |
| Ср.ариф | 1,618 | 1,618 | 1,617 | 1,616 |
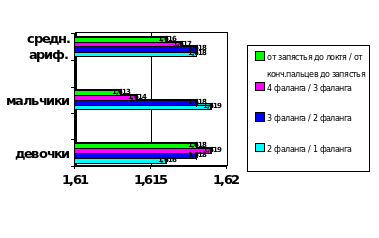
Вывод:
1. Проведя исследование, мы показали, что числа Фибоначчи и золотое сечение прослеживаются в строении нашего организма - в данном случае в строении кистей рук.
2. Пропорции тела человека формируются с годами
3.2. Анализ стихотворения
Анализ стихотворения А.С. Пушкина
Не дорого ценю я громкие права,
От коих не одна кружится голова.
Я не ропщу о том, что отказали боги
Мне в сладкой участи оспаривать налоги
Или мешать царям друг с другом воевать;
И мало горя мне, свободно ли печать
Морочит олухов, иль чуткая цензура
В журнальных замыслах стесняет балагура.
Все это, видите ль, слова, слова, слова.
Иные, лучшие, мне дороги права:
Иная, лучшая, потребна мне свобода:
Зависеть от царя, зависеть от народа –
Не все ли нам равно? Бог с ними.
Никому
Отчета не давать, себе лишь самому
Служить и угождать; для власти, для ливреи
Не гнуть ни совести, ни помыслов, ни шеи;
По прихоти своей скитаться здесь и там,
Дивясь божественным природы красотам,
И пред созданьями искусств и вдохновенья
Трепеща радостно в восторгах умиленья,
Вот счастье! Вот права ...
Одно из последних стихотворений Пушкина - "Не дорого ценю я громкие права..." состоит из 21 строки и в нем выделяется две смысловые части: в 13 и 8 строк. Характерно, что и первая часть этого стиха (13 строк) по смысловому содержанию делится на 8 и 5 строк, то есть все стихотворение построено по законам золотой пропорции. Преобладание в метрике стихотворений А.С. Пушкина чисел ряда Фибоначчи никак нельзя признать случайностью. Наличие этих чисел выражает одну из закономерностей творческого метода поэта, его эстетические требования, чувство гармонии.
После изучения золотого сечения в литературе нам стало интересно, проявляется ли оно и в стихах нашего времени.
Следует учесть, что законы стихосложения требуют, как правило, наличия четного числа строк в стихотворении, так как строки попарно рифмуются. Неудивительно, что стихотворения с числом строк в 12 и 14 встречаются гораздо чаще, чем с числом строк 13. Это же справедливо и для интервала 20-22 строки.
Стихи нашей пермской поэтессы Натальи Разбитновой
Родилась Наталья Разбитнова в Закамске 2 августа 1975 года. Детство провела в родном городе. Училась в школе № 69 (ныне гимназия № 6). С детства любила много читать, писала стихи и, как вспоминают педагоги, "была яркой, цельной, неординарной девочкой". Наталья училась в ПГУ на филологическом факультете. Более десяти лет работала постоянным корреспондентом газеты "Кировец", где писала статьи о культурной жизни города и искусстве.
Перелётная песня
Отпусти меня, пожалуйста, на волю!
Я устала, я измучена тоскою,
Я испугана безумием ветров…
Отпусти меня, не трать напрасных слов.
Отпусти меня, пожалуйста, не мучай:
Я так больше не могу… На всякий случай
Заходи почаще в Интернет,
Может встретишь там меня, а может, нет…
Отпусти меня — уже настала осень,
И свободного полёта крылья просят —
Над рекою, над тайгою и вперёд
Мой стремительный безудержный полёт.
Отпусти, не слушай злые крики чаек:
Я в разлуке по тебе почти скучаю,
И хрустальною слезинкой тает грусть:
Я весною обязательно вернусь…
В расцветающем саду тебя я встречу,
Просто выйду утром розовым на встречу —
Неожиданно-негаданно и вдруг…
Отпусти, меня, пожалуйста, на юг!
Анализ стихотворения:
В стихотворении 20 строк. В 12 строке заканчивается мысль, почему героиня просит, чтобы ее отпустили. 20:1,618=12 – золотое сечение. После 12 строки начинается новая мысль. Всего 107 cлов. Разделим 107:1,618=66 – золотое сечение, получаем «безудержный полет» - на этих словах также заканчивается основная мысль.
Вывод:
Рассчитав золотое сечение, мы видим, что указанная строчка является эмоциональной и смысловым центром произведения.
3.3 Анализ рекламы
После проведенных исследований в живописи нам стало интересно проанализировать рекламные щиты. Что будет находиться в определенных точках, невольно приковывающие наше внимание, так называемые зрительные центры. Таких точек всего четыре, они делят величину изображения по горизонтали и вертикали в золотом сечении, т.е. расположены они на расстоянии примерно 3/8 и 5/8 от соответствующих краев плоскости.
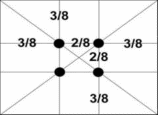



После проведенных исследований мы убедились, для того чтобы привлечь внимание главный элемент размещают в точках золотого сечения.
Глава 4. Заключение
Мы изучили проявление чисел Фибоначчи и связанного с ним закона золотого сечения в строении живых и неживых объектов.
Мы обнаружили удивительную математическую связь между числом спиралей у растений, числом веток в любой горизонтальной плоскости и числами в последовательности Фибоначчи. Мы увидели, как морфология различных организмов тоже подчиняется этому таинственному закону. Также мы увидели строгую математику в строении человека. Молекула ДНК человека, в которой зашифрована вся программа развития человеческого существа, дыхательная система, строение уха, - всё подчиняется определённым числовым соотношениям.
Мы узнали, что сосновые шишки, раковины улиток, волны океана, рога животных, облака циклона и галактики – все они образуют логарифмические спирали. Даже человеческий палец, который составлен из трех фаланг, находящихся по отношению друг к другу в Золотой пропорции, принимает спиральную форму, когда сжимается.
Вечность времени и световые годы космоса разделяют сосновую шишку и спиральную галактику, но строение остаётся тем же самым: коэффициент 1,618! Возможно, это первостепенный закон, управляющий природными явлениями.
Таким образом, наша гипотеза о существовании особых числовых закономерностей, которые отвечают за гармонию, подтверждается.
Действительно, всё в мире продуманно и просчитано самым главным нашим дизайнером – Природой!
Мы убедились, что у Природы есть свои законы, выраженные с помощью математики. И математика – это очень важный инструмент
для познания тайн природы.
Список литературы.
1. Воробьев Н. Н. Числа Фибоначчи. – М., Наука, 1984.
2. Гика М. Эстетика пропорций в природе и искусстве. – М., 1936.
3. Дмитриев А. Хаос, фракталы и информация. // Наука и жизнь, № 5, 2001.
4. Кашницкий С. Е. Гармония, сотканная из парадоксов // Культура и жизнь. – 1982.– № 10.
5. Малай Г. Гармония – тождество парадоксов // МН. – 1982.– № 19.
6. Соколов А. Тайны золотого сечения // Техника молодежи. – 1978.– № 5.
7. Стахов А. П. Коды золотой пропорции. – М., 1984.
8. Урманцев Ю. А. Симметрия природы и природа симметрии. – М., 1974.
9. Урманцев Ю. А. Золотое сечение // Природа. – 1968.– № 11.
10. Шевелев И.Ш., Марутаев М.А., Шмелев И.П. Золотое сечение/Три
взгляда на природу гармонии.-М., 1990.
11.Шубников А. В., Копцик В. А. Симметрия в науке и искусстве. -М.:
Наука, 1972.
1.http://www.chydesa-sveta.ru/en/chisla_fibonachchi.html
2.http://zagadkamozga.ru/node/630
3.http://magov.net/blog/3621.html
4.http://greenword.ru/2009/06/fibonacci-sequence.html
5.http://esopedia.ru/ChislaFibonachchi
6.http://reflection.org.ua/vselennaya/zagadka-chisel-fibonachi.html
7.http://dip-ref.ru/diplom/778.htm
8.http://evolutionoftruth.com/abennett
9.http://evolutionoftruth.com/goldensection/solarsys.htm
10.http://www.goldenmuseum.com/
11.http://www.mcs.surrey.ac.uk/Personal/R.Knott






 лава 1. Уникальная числовая последовательность Фибоначчи
лава 1. Уникальная числовая последовательность Фибоначчи 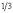 полного оборота - у орешника,
полного оборота - у орешника, 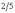 - у дуба,
- у дуба, 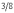 - у тополя и груши,
- у тополя и груши, 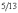 - у ивы.
- у ивы.