
1
Оглавление
Введение 3
ГЛАВА 1. История возникновения задач с параметрами 5
ГЛАВА 2. Методы решения заданий с параметром...................................................7
2.1. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ,АНАЛИТИЧЕСКИЙ МЕТОД.............................................7
2.2.графический метод..................................................................................................................8
2.2МЕТОД РЕШЕНИЯ ОТНОСИТЕЛЬНО ПАРАМЕТРА(XOA)..................................................8
Глава 3. Решение уравнения с параметром тремя способами 10
Глава 4. Виды уравнений с параметром........................................................................11
Заключение 12
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ................................................................................13
Введение
Задачи с параметрами относятся к существенной и важной части содержания современного математического образования. Они играют большую роль в формировании и развитии у учащихся логического мышления, а также математической культуры. Умение решать данные задания считается признаком высокого уровня знаний математики. Недостаточно простого применения «зазубренных» формул, необходимо понимание учениками закономерностей, наличие у них навыка анализа конкретного случая на основе общих свойств объекта, системности и последовательности. Зачастую оказывается, что выпускник школы не имеет представления о решении задач с параметрами. Отсюда возникает вопрос: почему же так происходит, ведь данный материал входит в итоговую аттестацию учащихся и как это исправить? Можно заметить, что в учебных программах по математике общеобразовательных школ задачам с параметрами отводится незначительное место, а реальное изучение таких задач начинается только в 11-м классе. Хотя данный материал можно вводить и изучать, начиная с линейных и квадратных уравнений (неравенств).
Это могут быть задания:
на нахождение решений в общем виде;
на определение корней, удовлетворяющих каким-либо свойствам;
на исследование количества корней в зависимости от значений параметра.
Кроме того, итоги выполнения задания № 18 Единого государственного экзамена показали, что его решают примерно 1–2% учащихся. Для решения данных заданий используются всем известные методы: аналитический и графический.
Актуальность темы исследования: Задачи с параметрами содержатся в контрольно-измерительных материалах Основного и Единого государственных экзаменов.
Противоречие в том, что для успешной сдачи ЕГЭ учащимся 10-11 классов необходимо знать , как решать различные уравнения с параметром, но школьный курс не подразумевает глубокого изучения данной темы.
Проблема: как подготовиться к решению заданий с параметрами из ЕГЭ.
Цель проекта: Рассмотреть способы решения различных примеров с параметром. Создать удобный и полный справочный материал для изучения способов решения примеров с параметром, который поможет выпускникам школ успешно аттестоваться по математике.
Задачи проекта:
1). Проанализировать представленный материал по решению примеров с параметром.
2). Найти оптимальный способ их решения, для дальнейшего предоставления его учащимся 10-11 классов.
3). Составить грамотный информационный продукт, который будет прост и понятен для восприятия.
1. История возникновения задач с параметрами
Подтверждение интереса к параметрическим задачам можно найти в учениях древнейших ученых. В астрономическом трактате «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой уже встречаются задачи на уравнения с параметром .
В алгебраическом трактате Ал-Хорезми дается классификация линейных и квадратных уравнений с параметром а. Автор насчитывает 6 видов уравнений, выражая их следующим образом:
- «Квадраты равны корням», т. е. αx2 = bx.
- «Квадраты равны числу», т. е. αx2 = c.
- «Корни равны числу», т. е. αx = c.
- «Квадраты и числа равны корням», т. е. αx2 + c = bx.
- «Квадраты и корни равны числу», т. е. αx2 + bx = c.
- «Корни и числа равны квадратам», т. е. αx2 + bx = c.
Формулы решения квадратных уравнений по Ал-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи, где была заложена основа аналитического метода решения уравнений с параметром.
Понятие переменной величины было введено в науку французским философом и математиком Рене Декартом (1596-1650). Именно Декарт пришел к идеям о единстве алгебры и геометрии и о роли переменных величин, Декарт ввел фиксированный единичный отрезок и стал рассматривать отношения других отрезков к нему – основа графического метода решения уравнений с параметром.
Понятие параметра: Параметр (от греческого слова parametron - отмеривающий) - величина, значение которой служат для различения некоторого множества между собой.
Определение: Параметром называется независимая переменная, значение которой в задаче считается заданным, фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству.
Под задачами с параметрами понимают задачи, в которых технический и логический ход решения и форма результата зависят от входящих в условие величин, численные значения которых не заданы конкретно, но должны считаться известными. Изучению задач с параметрами в школе отводится незначительное место, хотя неявно с этим понятием мы сталкиваемся уже при изучении функции y=kx. Для этой функции в качестве параметра выступает коэффициент k прямой пропорциональности. Если параметру, содержащемуся в уравнении (неравенстве) придать некоторое числовое значение, то возможен один из двух случаев:
- либо получится уравнение (неравенство), содержащее лишь данные числа и неизвестные, и не содержащие параметров;
- либо получится условие, лишенное смысла. В первом случае значение параметра называют допустимым , во втором - недопустимым. Определение: Уравнение с параметром – это семейство уравнений, определяемых параметром. Решить уравнение с параметром означает:
• Найти все значения параметра, при которых данное уравнение имеет решение.
• Найти все решения для каждого найденного значения параметра, то есть для неизвестного и параметра должны быть указаны свои области допустимых значений.
К основным методам решения линейных уравнений с параметром относятся аналитический метод и графический метод.
2. Методы решения заданий с параметром
2.1.АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ
АНАЛИТИЧЕСКИЙ МЕТОД
В процессе создания проекта, я прорешал большое количество различных уравнений с параметром, и нашел алгоритм для решения многих видов задач.Для решения уравнений данным алгоритмом, удобно знать решение хотя бы одной задачи этого типа. Продемонстрирую этот алгоритм.
Пример.
Найдите все значения a, при каждом из которых уравнение
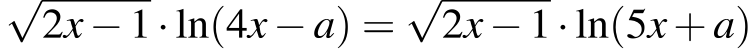
имеет ровно один корень на отрезке [0; 1].
Решение.
Исходное уравнение равносильно уравнению
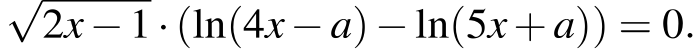
Рассмотрим два случая. Первый случай:
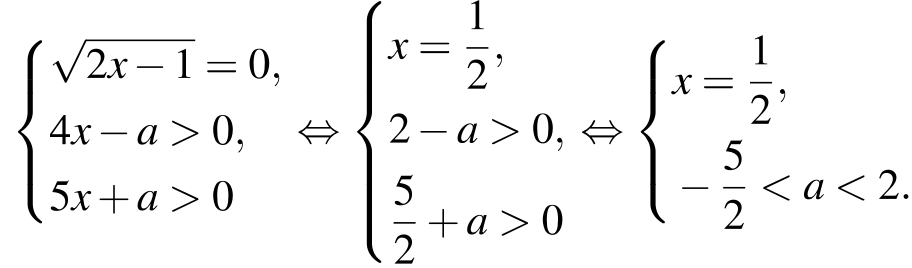
Второй случай:
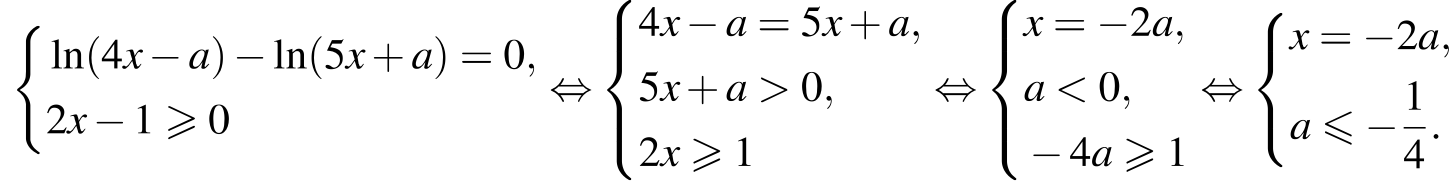
Корень уравнения x2 = −2a принадлежит отрезку [0; 1] при 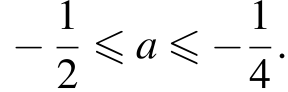 Корни уравнения
Корни уравнения 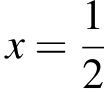 и
и 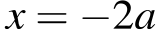 совпадают при
совпадают при 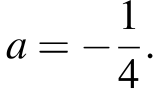
Получаем, что исходное уравнение имеет ровно один корень на отрезке [0; 1] при 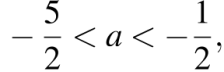 или
или 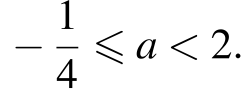
Для того чтобы найти количество корней на отрезке можно начертить прямую, на которой отметить корни, принадлежащие определенным отрезкам.
нет корней x1 x2 x1= x2 нет корней
нет корней x1 x1 x2 x1 нет корней
 -2,5 -0,5 -0,25 2 а
-2,5 -0,5 -0,25 2 а
Ответ: 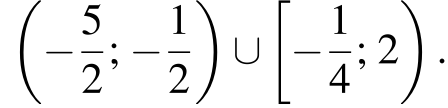
2.2.графический метод
МЕТОД РЕШЕНИЯ ОТНОСИТЕЛЬНО ПАРАМЕТРА(XOA)
Для решения уравнений с параметром графическим способом, необходимо изучить базовые элементы:
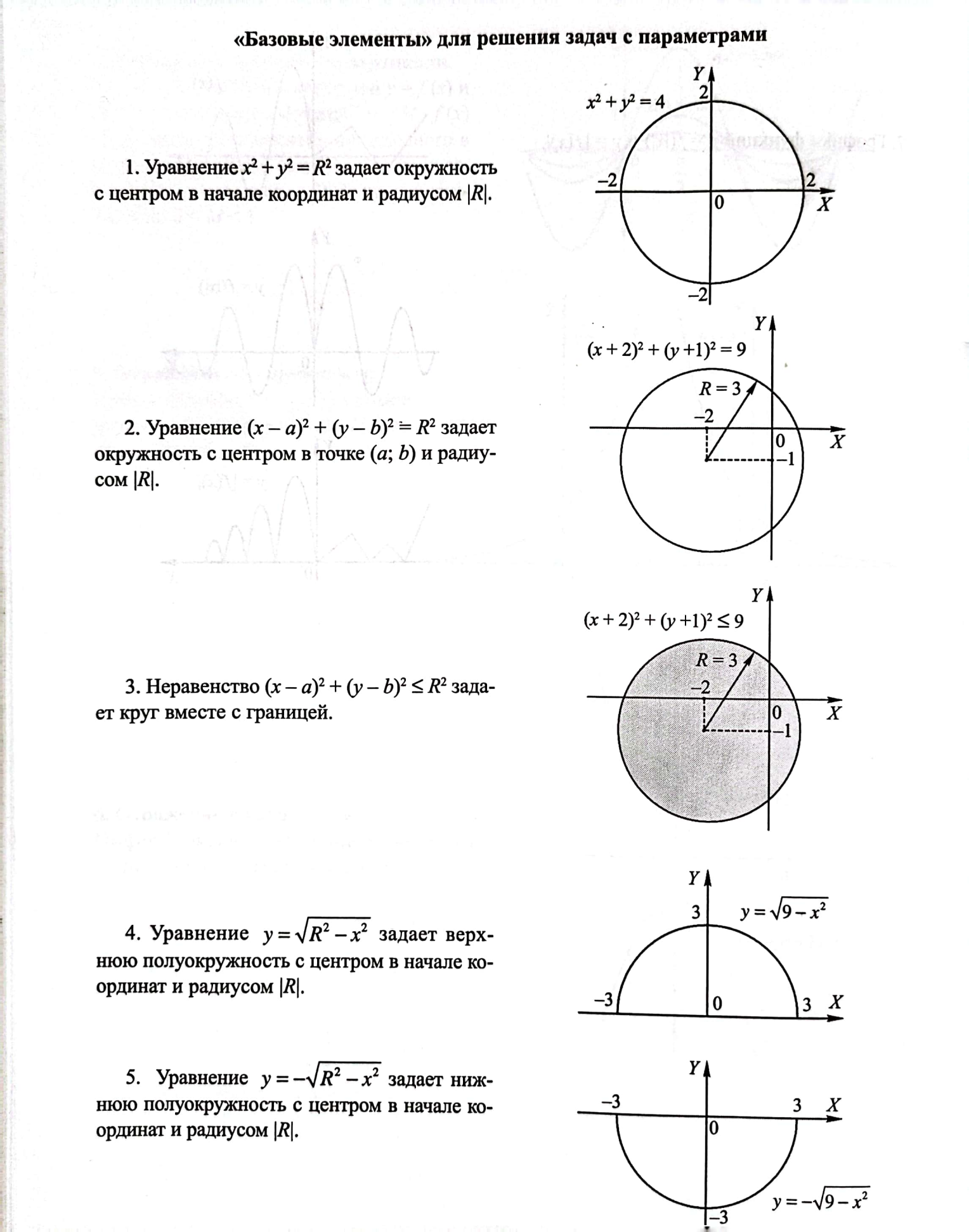
Пример:
Найдите все значения параметра а, при каждом из которых система
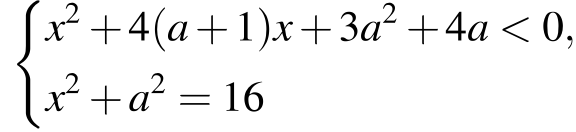
имеет решения.
Решение.
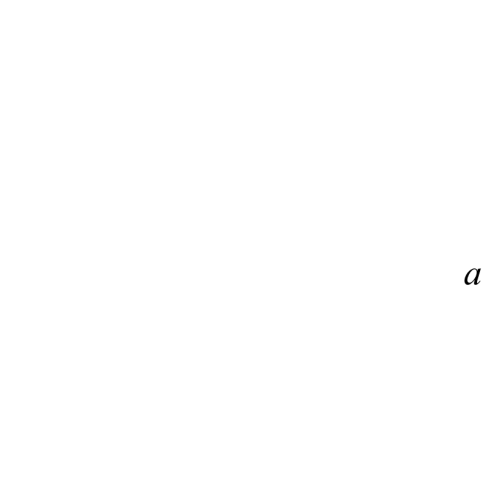
Разложим левую часть неравенства на множители: 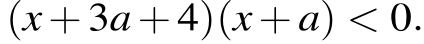 Поэтому неравенство задаёт пару вертикальных углов в плоскости Oax. Уравнение
Поэтому неравенство задаёт пару вертикальных углов в плоскости Oax. Уравнение 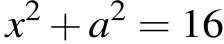 задаёт окружность с центром (0; 0) радиуса 4 в этой же плоскости. Решения системы — точки дуг окружности, лежащие в указанных вертикальных углах.
задаёт окружность с центром (0; 0) радиуса 4 в этой же плоскости. Решения системы — точки дуг окружности, лежащие в указанных вертикальных углах.
Абсциссы концов этих дуг находим из систем
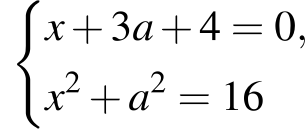 и
и 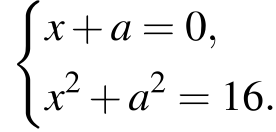
Из первой системы получаем: 
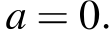 Из второй системы получаем:
Из второй системы получаем: 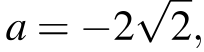
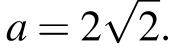
Ответ: 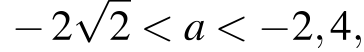
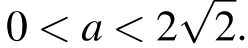
3.Решение уравнения Двумя способами
Найдите все значения k, при каждом из которых уравнение
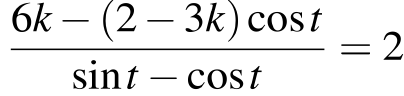
имеет хотя бы одно решение на отрезке 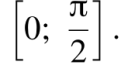
Аналитический метод
областью определения заданного уравнения являются все числа отрезка 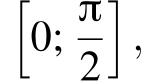 кроме точки, в которой
кроме точки, в которой 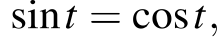 то есть кроме точки
то есть кроме точки 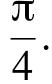 На этой области имеем:
На этой области имеем:
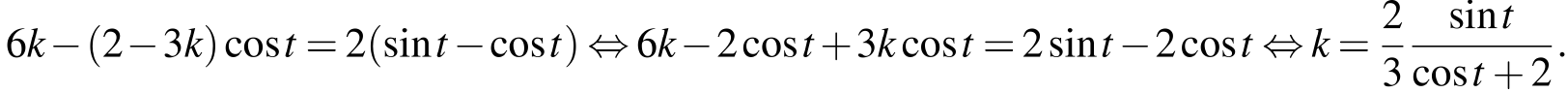
Найдём множество значений левой части. Пусть 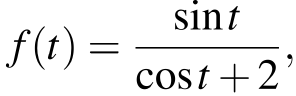 тогда
тогда
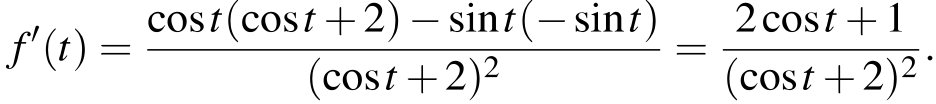
Найденная производная положительна на области определения уравнения, функция f (t) возрастает на ней, принимая все значения из отрезка 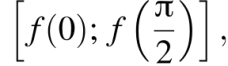 кроме значения
кроме значения 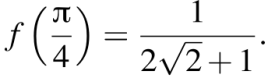 Тем самым,
Тем самым, 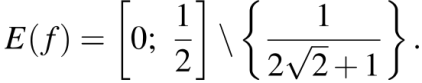
Следовательно, искомыми значениями параметра являются все числа из отрезка 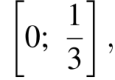 кроме
кроме 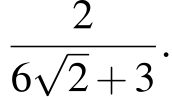
Графический метод
ОДЗ данного уравнения: 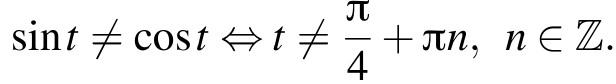
Задачу можно переформулировать так: найдите все значения k, при каждом из которых уравнение
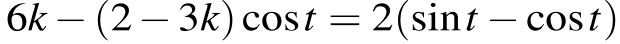
имеет на отрезке 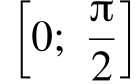 хотя бы одно решение, не равное
хотя бы одно решение, не равное 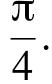
Преобразуем уравнение:

Обозначим 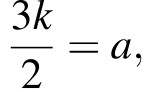 тогда последнее уравнение примет вид
тогда последнее уравнение примет вид 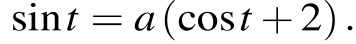 В системе координат, изображённой на рисунке, оно задаёт пучок прямых (отмечены оранжевым цветом), проходящих через точку
В системе координат, изображённой на рисунке, оно задаёт пучок прямых (отмечены оранжевым цветом), проходящих через точку 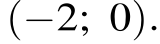
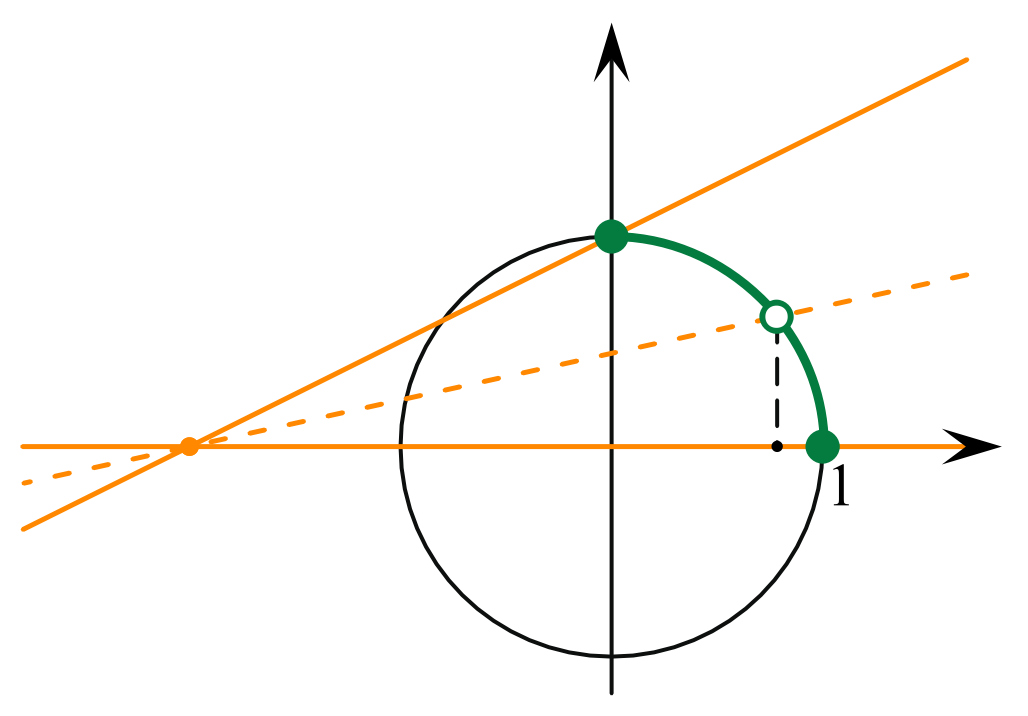
Точки пересечения этих прямых с тригонометрической окружностью представляют собой решения уравнения. Чтобы на промежутке 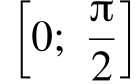 были решения, прямая должна пересекать дугу окружности, выделенную зелёным цветом, и не проходить через точку
были решения, прямая должна пересекать дугу окружности, выделенную зелёным цветом, и не проходить через точку 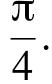
Угловой коэффициент горизонтальной прямой 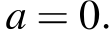
У прямой, проходящей через верхнюю точку дуги, угловой коэффициент 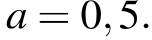
У прямой, проходящей через точку 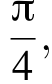 угловой коэффициент
угловой коэффициент 
Таким образом, условие задачи выполняется при 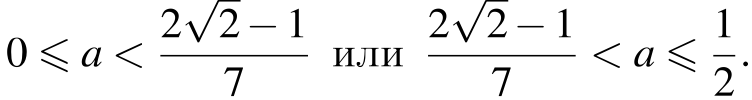
Вернувшись к параметру 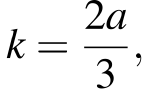 получаем:
получаем:
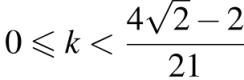 или
или 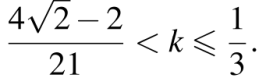
Таким образом, видно, что задание с параметром нужно решать, выбирая рациональный способ.
4. Виды уравнений с параметром
1)Рациональные уравнения с параметром;
Пример: Найдите все значения a, при которых уравнение
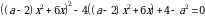
имеет ровно два решения.
2) Дробно-рациональные уравнения с параметром;
Пример: Найдите все значения a, при каждом из которых уравнение
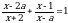 имеет ровно один корень.
имеет ровно один корень.
3) Уравнения с параметром, содержащие корни;
Пример:Найдите все значения a, при каждом из которых уравнение
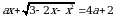 имеет единственный корень.
имеет единственный корень.
4)Уравнения с параметром, содержащие модуль;
Пример: Найдите все значения 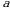 , при которых уравнение
, при которых уравнение 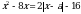 имеет ровно три решения.
имеет ровно три решения.
5)Тригонометрические уравнения с параметром;
Пример: Найдите все значения а, при каждом из которых уравнение
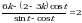 имеет хотя бы одно решение на отрезке
имеет хотя бы одно решение на отрезке 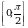 .
.
6) Показательные уравнения с параметром;
Пример:Найдите все значения а, при каждом из которых уравнение
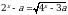 имеет единственный корень.
имеет единственный корень.
7) Логарифмические уравнения с параметром
Пример:При каких значениях параметра a уравнение
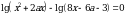 имеет единственное решение.
имеет единственное решение.
Заключение
В течении всего времени создания данного проекта: от задумки до реализации продукта - я узнавал все больше нюансов решения примеров с параметром и совершенствовал свои знания в данной теме. Я считаю, что данную тему хотя бы косвенно, но должен затронуть каждый учащийся 10-11 классов во время подготовки к Единому Государственному Экзамену. Ведь параметры встречаются гораздо чаще, чем мы можем себе представить.
Я пришел к выводу, что необходимо изучать данную тему более детально. Решение уравнений с параметром способствует развитию логического мышления человека, что позволит ему улучшить свои знания и умения. В моей работе рассмотрены часто встречающиеся типы уравнений, и я надеюсь, что знания, которые я получил в процессе работы, а также использовал при выполнении данной проектной работы, помогут мне и другим одиннадцатиклассникам при сдаче ЕГЭ.
Во время более детального рассмотрения данной темы я выделил для себя наиболее удобный подход к решению уравнений с параметром: аналитический. Я склоняюсь к использованию данного способа и во время сдачи профильного ЕГЭ по математике.
Список используемой литературы:
1) СдамГИА/РешуЕГЭ – образовательный портал для подготовки к
экзаменам.
2) ИНФОУРОК – ведущий образовательный портал России.
3) Википедия.
4) А. Шахмейстер «Задачи с параметрами в ЕГЭ» – «Петроглиф», №1 2004 г.
5). «ЕГЭ. Математика. Задания высокой и повышенной сложности» - Малкова А.Г.







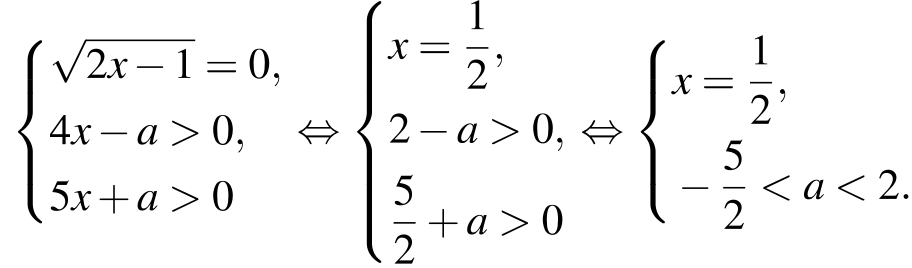
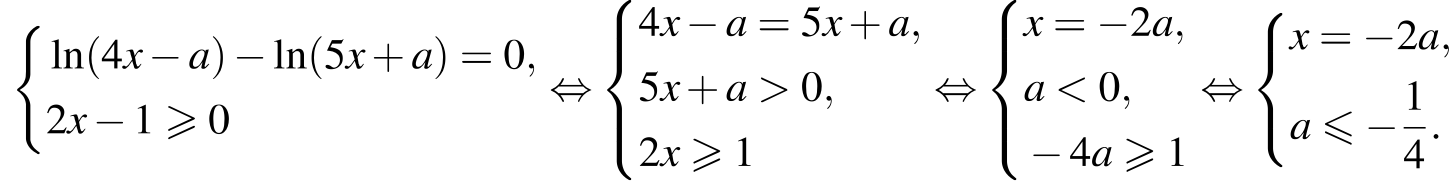
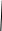
 -2,5 -0,5 -0,25 2 а
-2,5 -0,5 -0,25 2 а
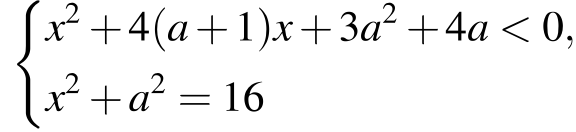
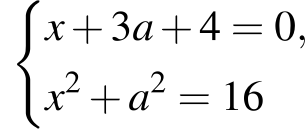 и
и 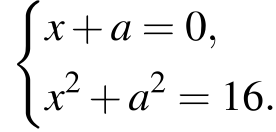

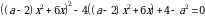
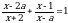 имеет ровно один корень.
имеет ровно один корень.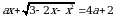 имеет единственный корень.
имеет единственный корень.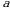 , при которых уравнение
, при которых уравнение 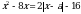 имеет ровно три решения.
имеет ровно три решения.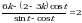 имеет хотя бы одно решение на отрезке
имеет хотя бы одно решение на отрезке 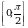 .
.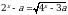 имеет единственный корень.
имеет единственный корень.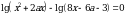 имеет единственное решение.
имеет единственное решение.









