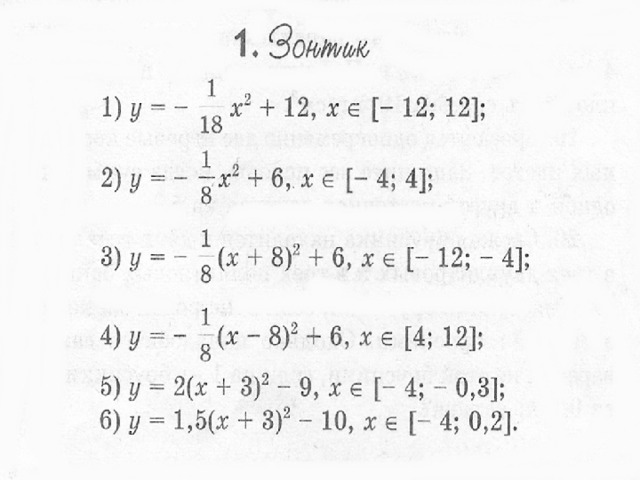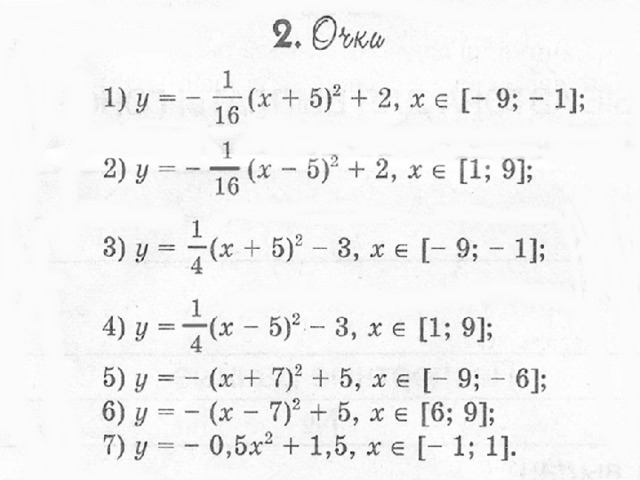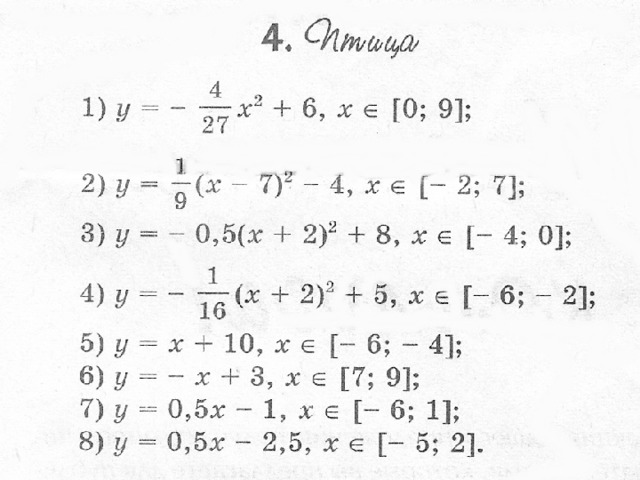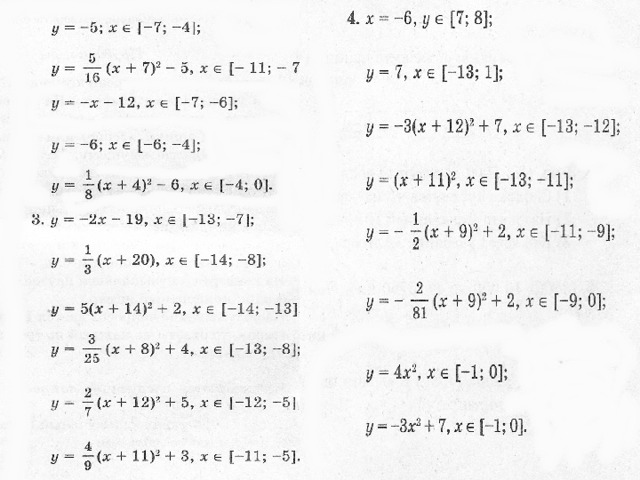Проектная работа "Рисунки в графиках"

Проектная работа Рисунки в графиках Авторы: Расулова Лейла Руководитель: Зенина Е.Н. (Данилина Е.Н.) МОУ «Гимназия №4» 2019-2020 уч.год.

Введение.

Тема нашего проекта называется «Рисунки в графиках». Мы выбрали этот проект так как знали, что существует декартова система координат на плоскости и умели строить некоторые графики функций. Нам стало интересно сможем ли мы построить различные фигуры с помощью известных нам графиков? Эти вопросы нас заинтересовали и мы решили работать над данным проектом.

Таким образом, мы поставили перед собой цель: научиться строить фигуры с помощью графиков функций в декартовой системе координат.

Для достижения цели, мы наметили план работы и сформулировали задачи, способствующие раскрытию творческих способностей каждого из нас, взаимопонимания, индивидуальности.

Задачи проекта:

• научиться строить фигуры с помощью графиков в декартовой системе координат, расширив свой кругозор и продолжив работу над графической культурой;
• научиться работать с различными источниками информации;
• научиться составлять презентации, используя навыки работы с компьютером;
• научиться выступать перед аудиторией.

В процессе работы над проектом, мы обращались к математическому словарю, учебникам по высшей математике, методической литературе, интернету. Построили каждый по двефигуры в системе координат с помощью графиков функций, и одну общую фигуру, описали их и выполнили соответствующие построения, т.е. выполнили творческие работы, наглядно показав степень овладения полученной информацией.

Элементарные функции и их графики.

1). Пропорциональные величины . Если переменные y и x прямо пропорциональны, то функциональная зависимость между ними выражается уравнением:

y = k x, где k - постоянная величина ( коэффициент пропорциональности ).

График прямой пропорциональности – прямая линия, проходящая через начало координат и образующая с осью X угол , тангенс которого равен k : tan = k ( рис.8 ). Поэтому, коэффициент пропорциональности называется также угловым коэффициентом. На рис.8 показаны три графика для k = 1/3, k = 1 и k = -3.

2. Линейная функция . Если переменные y и x связаны уравнением 1-ой степени:A x + B y = C , где по крайней мере одно из чисел A или B не равно нулю, то графиком этой функциональной зависимости является прямая линия. Если C = 0, то она проходит через начало координат, в противном случае - нет. Графики линейных функций для различных комбинаций A, B, C показаны на рис.9.

3. Обратная пропорциональность . Если переменные y и x обратно пропорциональны, то функциональная зависимость между ними выражается уравнением: y = k / x , где k - постоянная величина. График обратной пропорциональности – гипербола ( рис.10 ). У этой кривой две ветви. Гиперболы получаются при пересечении кругового конуса плоскостью ( о конических сечениях см. раздел «Конус» в главе «Стереометрия» ). Как показано на рис.10, произведение координат точек гиперболы есть величина постоянная, в нашем примере равная 1. В общем случае эта величина равна k, что следует из уравнения гиперболы: xy = k.

4. Квадратичная функция . Это функция: y = ax ² + bx + c, где a, b, c - постоянные, a 0. В простейшем случае имеем: b = c = 0 и y = ax². График этой функции квадратная парабола - кривая, проходящая через начало координат ( рис.11 ). Каждая парабола имеет ось симметрии OY, которая называется осью параболы. Точка O пересечения параболы с её осью называется вершиной параболы.

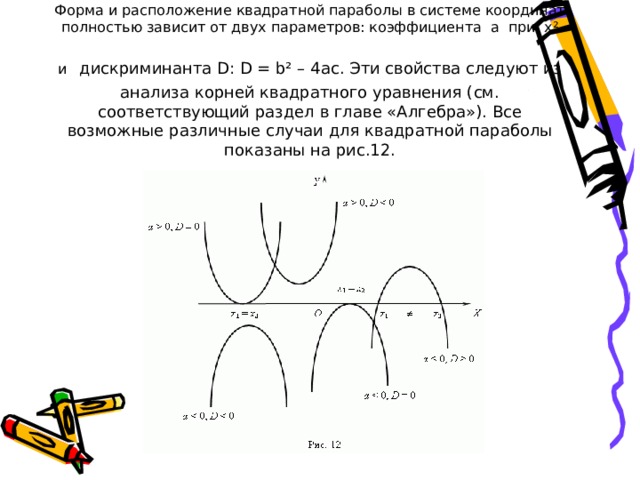
Форма и расположение квадратной параболы в системе координат полностью зависит от двух параметров: коэффициента a при x² и дискриминанта D: D = b² – 4ac. Эти свойства следуют из анализа корней квадратного уравнения (см. соответствующий раздел в главе «Алгебра»). Все возможные различные случаи для квадратной параболы показаны на рис.12.

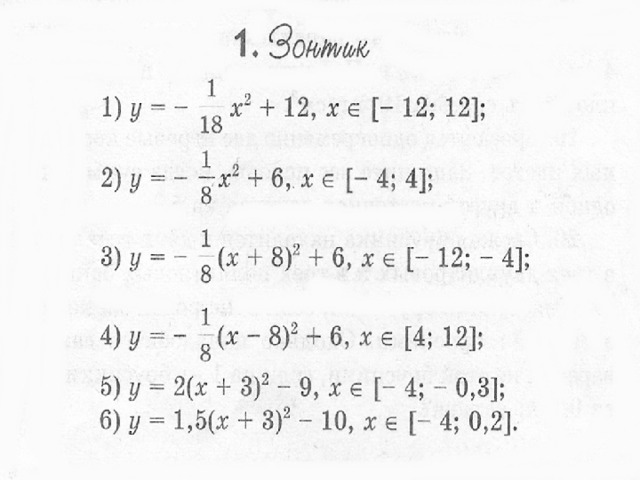
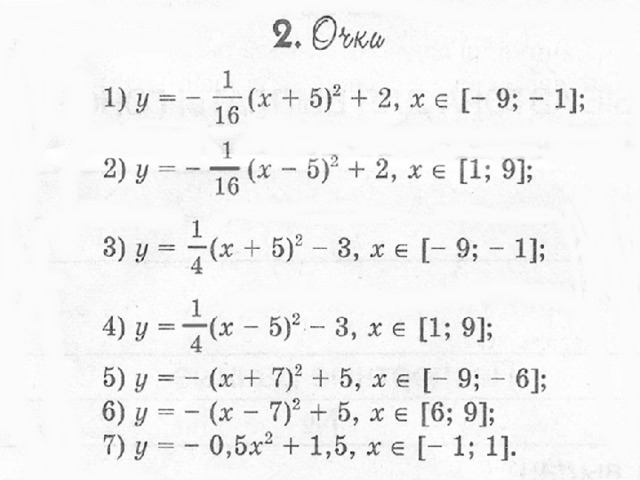
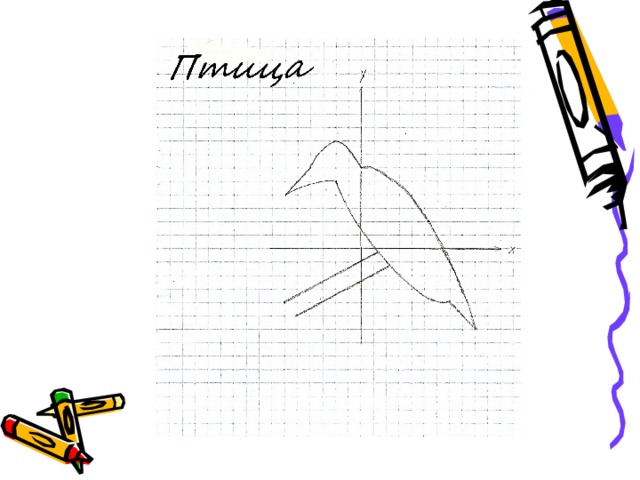
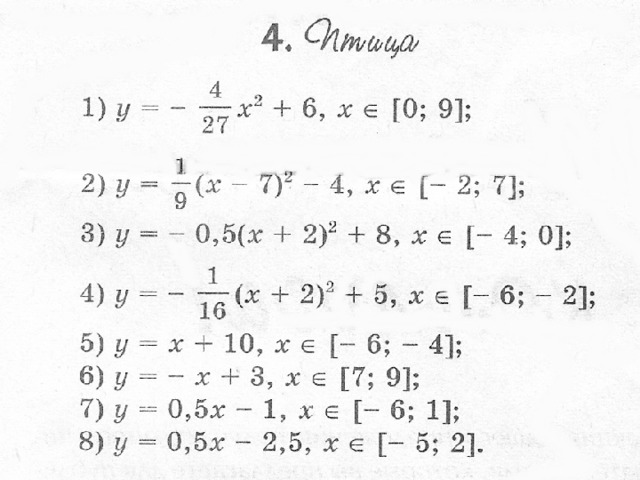
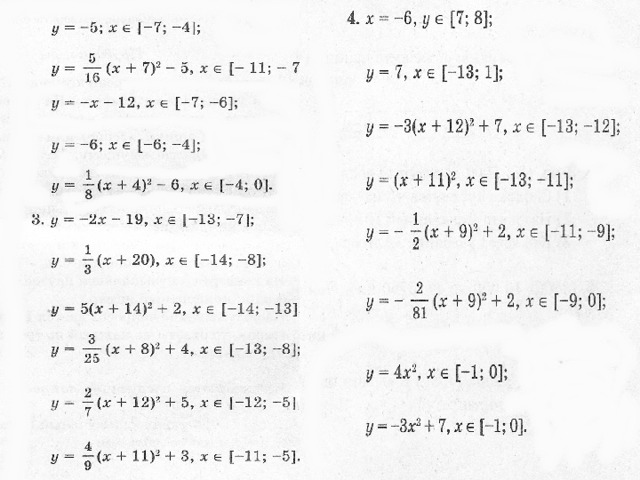
Заключение. Таким образом, при работе над проектом «Рисунки в графиках» мы научились строить фигуры с помощью графиков функций, заданных каждый своей формулой на рассматриваемых промежутках.

При выполнении творческих работ, мы:

• придумали и построили каждый свой рисунок;
• описали этот рисунок;
• проверили друг у друга выполненные творческие работы и внесли, если это необходимо, соответствующие коррективы;
• оформили результаты на листах;
• составили презентации своих творческих работ.

Выполняя творческие работы, мы закрепили навыки вычислительной техники; показали степень овладения графической культурой, хотя это было нелегко.

Наш проект имеет свою практическую направленность:

• создание дидактического материала;
• расширение кругозора;
• закрепление навыков графических построений;
• использование материалов проектной работы при проведении уроков;
• поиск и отбор информации.

Спасибо за внимание