РИСУЕМ УРАВНЕНИЯМИ
Помазкина Екатерина,
ученица 7в класса
МАОУ СОШ № 4
Недавно передвигаясь из школы на танцы в машине у дедушки, я услышала песню «Где же моя черноглазая, где, в Вологде-где-где-где, в Вологде где, в доме, где резной палисад». Тут же перед глазами возник уютный домик в окружении цветов на одной из улиц Вологды. «А как найти этот домик? Наверно только по адресу?», – подумала я.
Из дошкольного детства вспоминается еще случай, когда мы с родителями пошли в кинотеатр. Тогда, войдя в зал, у меня, можно сказать, глаза разбежались - куда же сесть, какое место выбрать? Родители меня остановили: «Это твоё место: ряд 8, место 16». Получается, что и в кинотеатре бывают адреса!
Какое же было у меня удивление, когда с адресами мы встретились на уроках математики и географии в шестом классе – оказывается их можно назвать координаты. С координатами в жизни мы сталкиваемся постоянно, можно сказать «на каждом шагу».
Но меня заинтересовал вопрос – а где еще можно использовать координаты. Учитель мне предложил применить свои знания при решении уравнений.
Тема «Уравнения» непростая, потому, что мы часто ошибаемся при счете, а использование координат даст возможность всем ученикам «видеть» ошибки и исправлять их.
Объект исследования: решение линейных уравнений
Предмет нашего исследования: практическая работа по решению линейных уравнений на координатной плоскости
В работе были использованы методы анализа, изучения различных литературных и интернет источников, наблюдения, опросы.
В моей работе первая часть посвящена вопросам истории координатной плоскости и уравнений. Во второй части описан процесс работы по созданию картины на координатной плоскости с использованием уравнений.
Хотелось бы несколько слов сказать об истории рассматриваемой темы
Еще за 200 лет до нашей эры греческий ученый Гиппарх ввёл географические координаты. Он предложил нарисовать на географической карте параллели и меридианы и обозначить числами широту и долготу. С помощью этих двух чисел можно точно определить положение острова, поселка, горы или колодца в пустыне и нанести их на карту или глобус. Научившись определять в открытом мире широту и долготу местонахождения корабля, моряки получили возможность выбирать нужное им направление.
31 марта 1596 родился французский философ, математик, физик Рене Декарт. Систему координат, изучаемую в школе, называют прямоугольной декартовой системой координат – в честь этого французского математика. В качестве координатных осей берутся прямые, перпендикулярные друг другу, то система координат называется прямоугольной.
Координаты используются в практической деятельности человека.
Например, в информатике: Рисунки, схемы, чертежи, графики – графические формы представления информации. Метод кодирования – это один из удобных способов представления числовой информации с помощью графиков, которые строятся в различных системах координат.
Инженерной графике. Координатные системы разных видов применяют для моделирования эскизов промышленных машин, оборудования, объектов на местности.
Биологии. Построение схем молекул, построение диаграмм и графиков, прослеживающих эволюцию развития.
Говоря об уравнениях стоит отметить, что некоторые алгебраические приемы решения линейных уравнений были известны еще 4000 лет назад в Древнем Вавилоне. В древних математических задачах Междуречья, Индии, Китая, Греции неизвестные величины выражали число павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущества. В XVI в. Франсуа Виета первым из математиков ввел буквенные обозначения для коэффициентов уравнения и неизвестных величин. А традицией обозначать неизвестные величины последними буквами латинского алфавита мы обязаны соотечественнику Виета – известному нам Рене Декарту.
Благодаря всем перечисленным математикам сегодня мы можем отмечать координаты и решать уравнения
Для того, чтобы научиться решать уравнения нужно решать много и внимательно проверять свои ошибки. Но не всегда интересно, поэтому мы, посоветовавшись с учителем, решили сделать эту работу интересней: раз рисовать нравится по координатам всем, то сделаем так, чтобы был рисунок по уравнениям.
Для своей картины мы взяли сюжет из песни про Черепаху и Львенка, немного изменив сюжет.
Каждый рисунок записан в координатах. К одной из координат точки по каждому рисунку составлено уравнение. Вот так:
Рисунок 7 Чайка
| Координата | Уравнение | Ответы в координатах |
| (27;y) | 5x+52=150 | (27;25) |
| (25;y) | 5x=125 | (25;25) |
| (24;y) | x-4=20 | (24;24) |
| (25;y) | 3x=81 | (25;27) |
| (27;y) | 5x+52=150 | (27;25) |
| (27;y) | x:4+15=22 | (27;28) |
| (30;y) | 2x-18=x+11 | (30;29) |
| (27;y) | 5x=125 | (27;25) |
Составив уравнения для всех точек, мы получили следующую картину:
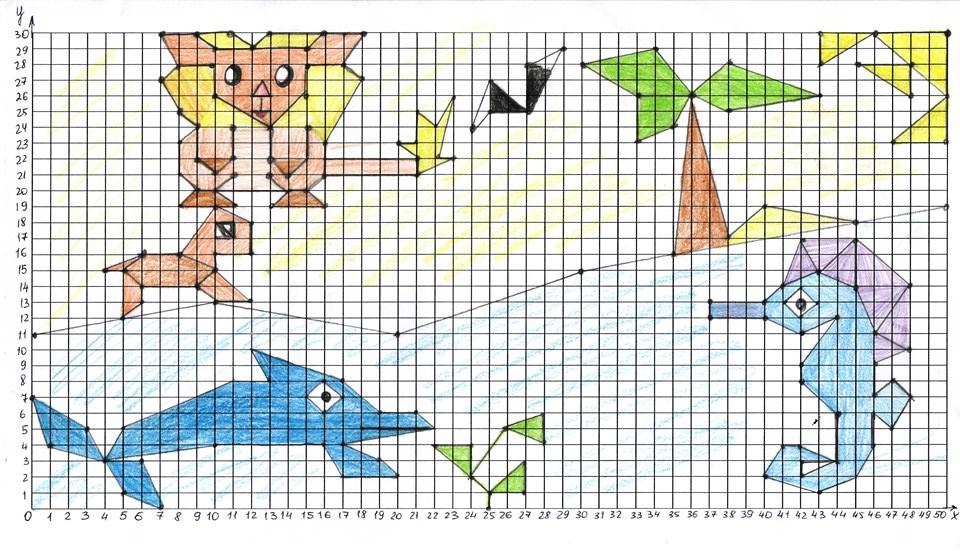
Рисование на координатной плоскости увлекательнейшее занятие. Мы хотели сделать увлекательной тему «Решение уравнений» и я думаю, что данная работа удалась – мы картину нарисовали уравнениями. Возможно, она получилась не очень красивая. Но это значит – ее можно дальше совершенствовать и уточнять, добавляя новые координаты и уравнения.
Один из известных ученых сказал: «Математика остаётся олицетворением науки, символом мудрости, царицей всех наук. Красота математики среди наук недосягаема, а красота является одним из связующих звеньев науки и искусства». Я согласна с этим высказыванием – ведь мы можем даже скучную работу превратить в интересное занятие, зная математику.
Думаю, что данную работу можно использовать не только в седьмых, но и в более старших классах с целью повторения темы «Уравнения». Кроме этого для рисования и решения уравнений можно попробовать использовать компьютер. Следовательно, у данной темы есть будущее.


















