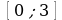Учитель математики Мамона Т.П.
Тема: Производная и её применение
Цель урока: обобщить и систематизировать материал по теме «Производная и её применение»; подготовить обучающихся к контрольной работе; развивать умение анализировать и обобщать изученный материал; навыки общения в группе; воспитывать самостоятельность, взаимоуважение.
Ожидаемые результаты: обучающиеся должны понимать значение понятия производная для описания реальных процессов; находить угловой коэффициент и угол наклона касательной к графику функции в данной точке; скорость изменения величины в точке; дифференцировать функции; применять производную для исследования функции на монотонность и экстремум; находить наибольшее и наименьшее значения функции.
Оборудование: учебник, раздаточный материал
Тип урока: обобщение и систематизация знаний
Ход урока
Организационный этап
Учитель объединяет обучающихся в группы.
Проверка домашнего задания
В процессе проверки домашнего задания обучающиеся повторяют правила дифференцирования, алгоритм нахождения промежутков монотонности и точек экстремума, алгоритм нахождения наибольшего и наименьшего значений функции, нахождение критических точек.
Формулировка темы, цели и заданий урока; мотивация учебной деятельности
Сегодня знания темы «Производная и её применение» будут обобщены. Это позволит вам лучше увидеть, какие вопросы темы требуют большего внимания и коррекции. Нужно подготовиться к контрольной работе максимально тщательно.
Повторение и анализ фактов
Фронтальный опрос по технологии «Микрофон»
Дайте определение производной.
Что такое производная с геометрической точки зрения?
Что такое производная с механической точки зрения?
Запишите уравнение касательной к графику функции 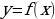 в точке с абсциссой
в точке с абсциссой 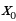 .
.
Сформулируйте определение критических точек функции.
Сформулируйте достаточное условие возрастания (убывания) функции.
Дайте определение точек экстремума функции.
Сформулируйте необходимое условие экстремума функции.
Сформулируйте достаточное условие существования экстремума в точке.
По какому алгоритму решается задача на нахождение наибольшего и наименьшего значений функции на промежутке 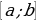 ?
?
Совершенствование умений и навыков
Работа в группах.
По окончании времени, которое определяет учитель, представитель каждой группы защищает у доски решение одного из заданий.
Карточка для работы группы
1. Точка движется прямолинейно по закону 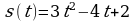 . Найти: а) скорость точки в произвольный момент времени
. Найти: а) скорость точки в произвольный момент времени 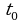 ; б) скорость точки в момент времени
; б) скорость точки в момент времени 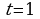 с.
с.
2. Написать уравнение касательной к графику функции 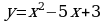 в точке
в точке 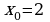 .
.
3. Исследовать функцию 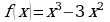 и построить схематически её график.
и построить схематически её график.
4. Найти наибольшее и наименьшее значения функции 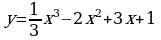 на промежутке
на промежутке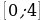 .
.
Решение:
1. Поскольку 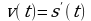 , то в этом случае
, то в этом случае 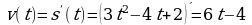 . Тогда
. Тогда 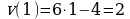
Ответ: а) 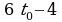 ; б) 2 м/с
; б) 2 м/с
2. Уравнение касательной к графику функции 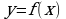 в точке
в точке 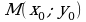 имеет вид
имеет вид 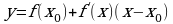
1) находим производную функции 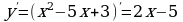
2) вычисляем значение производной в точке 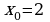
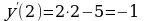
3) находим значение функции в заданной точке 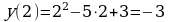
4) подставляем эти значения в уравнение касательной
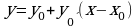 , имеем
, имеем 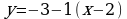 ,
, 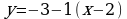 - уравнение касательной
- уравнение касательной
Ответ: 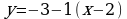
3. 1) Область определения функции 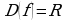
2) Найдем точки пересечения графика функции с координатными осями.
При пересечении с осью 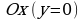

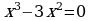 ,
, 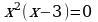
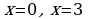
При пересечении с осью 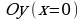 имеем
имеем 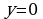 . В точке
. В точке 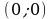 график функции пересекает ось
график функции пересекает ось 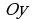 .
.
3) Находим производную 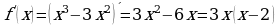
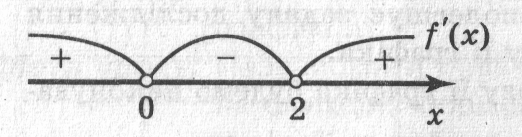 Находим критические точки
Находим критические точки 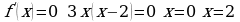
4) Находим промежутки монотонности функции
5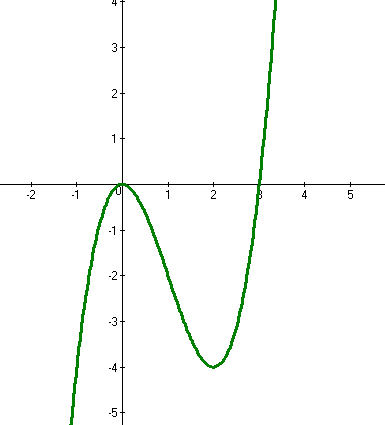 ) Находим экстремум функции
) Находим экстремум функции 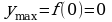 ,
, 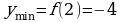
6) Используя результаты исследования, строим график функции 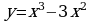
4. Функция 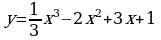 определена и дифференцирована на промежутке
определена и дифференцирована на промежутке 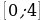 .
.
Найдем производную заданной функции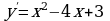 . Решив уравнение
. Решив уравнение 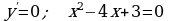 , находим критические точки функции
, находим критические точки функции 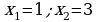 - оба корня принадлежат отрезку
- оба корня принадлежат отрезку 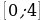 . Вычислим значения функции на концах отрезка и в критических точках:
. Вычислим значения функции на концах отрезка и в критических точках: 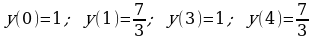 .
.
Ответ: 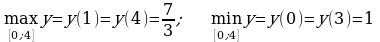 .
.
Подведение итога урока
Беседа.
1. Нравится ли вам групповая форма работы?
2. Была ли достигнута цель урока?
3. На какие задания нужно обратить больше внимания во время подготовки к контрольной работе?
4. В чем причина трудностей на уроке? Как устранить пробелы в знаниях?
Домашнее задание.
Выполнить домашнюю контрольную работу.
Найдите промежутки возрастания и убывания функции 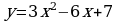
Найдите экстремумы функции 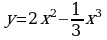
Исследуйте функцию 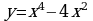 и постройте её график.
и постройте её график.
Составьте уравнение касательной к графику функции 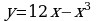 в точке с абсциссой
в точке с абсциссой 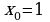
Найдите наибольшее и наименьшее значения функции 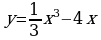 на отрезке
на отрезке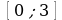






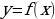 в точке с абсциссой
в точке с абсциссой 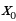 .
.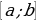 ?
?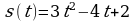 . Найти: а) скорость точки в произвольный момент времени
. Найти: а) скорость точки в произвольный момент времени 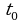 ; б) скорость точки в момент времени
; б) скорость точки в момент времени 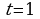 с.
с.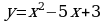 в точке
в точке 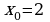 .
.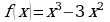 и построить схематически её график.
и построить схематически её график. 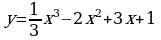 на промежутке
на промежутке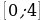 .
.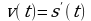 , то в этом случае
, то в этом случае 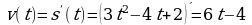 . Тогда
. Тогда 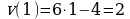
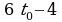 ; б) 2 м/с
; б) 2 м/с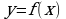 в точке
в точке 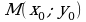 имеет вид
имеет вид 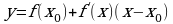
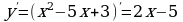
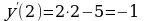
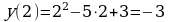
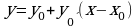 , имеем
, имеем 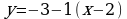 ,
, 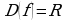
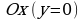

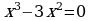 ,
, 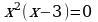
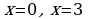
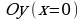 имеем
имеем 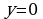 . В точке
. В точке 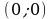 график функции пересекает ось
график функции пересекает ось 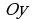 .
.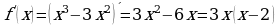
 Находим критические точки
Находим критические точки 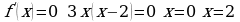
 ) Находим экстремум функции
) Находим экстремум функции 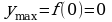 ,
, 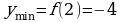
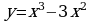
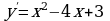 . Решив уравнение
. Решив уравнение 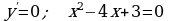 , находим критические точки функции
, находим критические точки функции 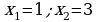 - оба корня принадлежат отрезку
- оба корня принадлежат отрезку 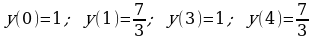 .
.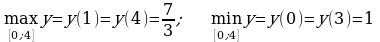 .
.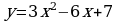
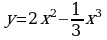
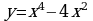 и постройте её график.
и постройте её график.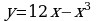 в точке с абсциссой
в точке с абсциссой 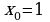
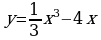 на отрезке
на отрезке