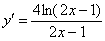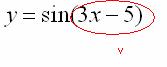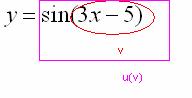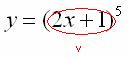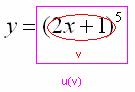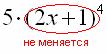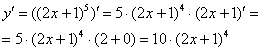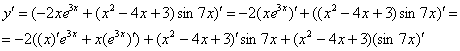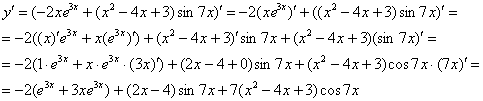Производная сложной функции

Уважаемые студенты! В данном ниже материале более подробно рассмотрена тема «Нахождение производной сложной функции» (параграф 46, пункт 5 в учебнике). Внимательно изучите и выполните задания.

- запишите тему «Нахождение производной сложной функции»

- Запишите формулу (5) из параграфа 46 учебника. Она аналогична формуле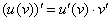

- перенесите в тетрадь примеры решения без словесных пояснений. Решение, например, первого задания должно выглядеть так: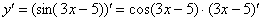

- выполните номера учебника: 831 – 839, 845 – 848. (Задание рассчитано на 2 пары + Д/З)

- выполненные задания сфотографировать или отсканировать и прислать на почту, указав в теме фамилию и тему работы

Производная сложной функции. Примеры решений

На данном уроке мы научимся находить производную сложной функции. Урок является логическим продолжением занятия Как найти производную?, на котором мы разобрали простейшие производные, а также познакомились с правилами дифференцирования и некоторыми техническими приемами нахождения производных. Таким образом, если с производными функций у Вас не очень или какие-нибудь моменты данной статьи будут не совсем понятны, то сначала ознакомьтесь с вышеуказанным уроком. Пожалуйста, настройтесь на серьезный лад – материал не из простых, но я все-таки постараюсь изложить его просто и доступно.

На практике с производной сложной функции приходится сталкиваться очень часто, я бы даже сказал, почти всегда, когда Вам даны задания на нахождение производных.

Смотрим в таблицу на правило (№5) дифференцирования сложной функции:

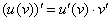
Разбираемся. Прежде всего, обратим внимание на запись 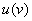 . Здесь у нас две функци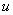и –   и 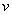 , причем функция  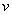, образно говоря, вложена в функцию  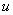. Функция такого вида (когда одна функция вложена в другую) и называется сложной функцией.

Функцию 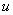  я буду называть внешней функцией, а функцию  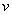 – внутренней (или вложенной) функцией.

! Данные определения не являются теоретическими и не должны фигурировать в чистовом оформлении заданий. Я применяю неформальные выражения «внешняя функция», «внутренняя» функция только для того, чтобы Вам легче было понять материал.

Для того, чтобы прояснить ситуацию, рассмотрим:

Пример 1

Найти производную функции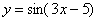 

Под синусом у нас находится не просто буква «икс», а целое выражение 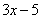 , поэтому найти производную сразу по таблице не получится. Также мы замечаем, что здесь невозможно применить первые четыре правила, вроде бы есть разность, но дело в том, что «разрывать на части» синус нельзя:

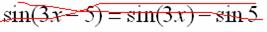
В данном примере уже из моих объяснений интуитивно понятно, что функция 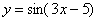  – это сложная функция, причем многочлен  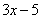 является внутренней функцией (вложением), а  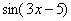 – внешней функцией.

Первый шаг, который нужно выполнить при нахождении производной сложной функции состоит в том, чтобы разобраться, какая функция является внутренней, а какая – внешней.

В случае простых примеров вроде 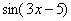  понятно, что под синус вложен многочлен  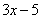. А как же быть, если всё не очевидно? Как точно определить, какая функция является внешней, а какая внутренней? Для этого я предлагаю использовать следующий прием, который можно проводить мысленно или на черновике.

Представим, что нам нужно вычислить на калькуляторе значение выражения 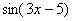  при 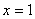  (вместо единицы может быть любое число).

Что мы вычислим в первую очередь? В первую очередь нужно будет выполнить следующее действие: 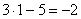 , поэтому многочлен  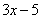 и будет внутренней функцией  :
 
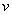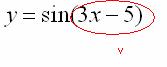
Во вторую очередь нужно будет найти 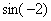 , поэтому синус – будет внешней функцией:

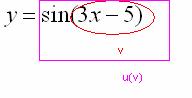
После того, как  мы РАЗОБРАЛИСЬ с внутренней и внешней функциями самое время применить правило дифференцирования сложной функции  .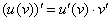

Начинаем решать. Из урока Как найти производную? мы помним, что оформление решения любой производной всегда начинается так – заключаем выражение в скобки и ставим справа вверху штрих:

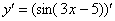
Сначала находим производную внешней функции 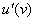  (синуса), смотрим на таблицу производных элементарных функций и замечаем, что  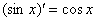. Все табличные формулы применимы и в том, случае, если «икс» заменить сложным выражением, в данном случае:

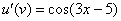
Обратите внимание, что внутренняя функция 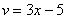  не изменилась, её мы не трогаем.

Ну и совершенно очевидно, что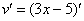 

Результат применения формулы 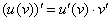  в чистовом оформлении выглядит так:

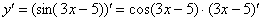
Далее мы берем производную внутренней функции, она очень простая:

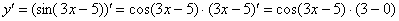
Постоянный множитель обычно выносят в начало выражения:

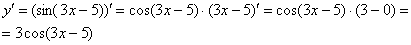
Готово

Если осталось какое-либо недопонимание, перепишите решение на бумагу и еще раз прочитайте объяснения.

Пример 2

Найти производную функции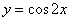 

Это пример для самостоятельного решения (ответ в конце урока).

Пример 3

Найти производную функции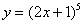 

Как всегда записываем:

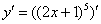
Разбираемся, где у нас внешняя функция, а где внутренняя. Для этого пробуем (мысленно или на черновике) вычислить значение выражения 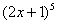  при 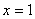 . Что нужно выполнить в первую очередь? В первую очередь нужно сосчитать чему равно основание:  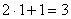, значит, многочлен  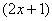 – и есть внутренняя функция:

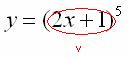
И, только потом выполняется возведение в степень 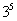 , следовательно, степенная функция – это внешняя функция:

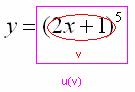
Согласно формуле 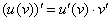 , сначала нужно найти производную от внешней функции, в данном случае, от степени. Разыскиваем в таблице нужную формулу:  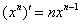. Повторяем еще раз: любая табличная формула справедлива не только для «икс», но и для сложного выражения. Таким образом, результат применения правила дифференцирования сложной функции  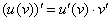  следующий:

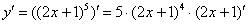
Снова подчеркиваю, что когда мы берем производную от внешней функции 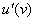 , внутренняя функция  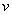 у нас не меняется:

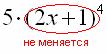
Теперь осталось найти совсем простую производную от внутренней функции и немного «причесать» результат:

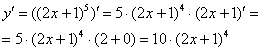
Готово.

Пример 4

Найти производную функции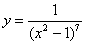 

Это пример для самостоятельного решения (ответ в конце урока).

Пример 5

Найти производную функции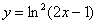 

Это пример для самостоятельного решения (ответ в конце урока).

На практике правило дифференцирования сложной функции почти всегда применяется в комбинации с остальными правилами дифференцирования.

Пример 6

Найти производную функции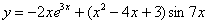 

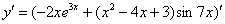
Сначала используем правило дифференцирования суммы 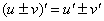 , заодно в первом слагаемом выносим постоянный множитель за знак производной по правилу  :

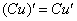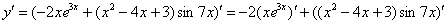
В обоих слагаемых под штрихами у нас находится произведение функций, следовательно, нужно дважды применить правило  :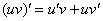

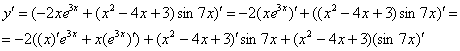
Замечаем, что под некоторыми штрихами у нас находятся сложные функции 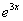 ,  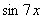. Каламбур, но это простейшие из сложных функций, и при определенном опыте решения производных Вы будете легко находить их устно.
А пока запишем подробно, согласно правилу 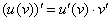 , получаем:

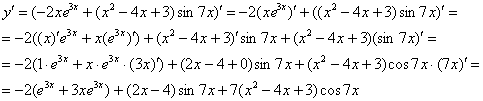
Готово.

! Обратите внимание на приоритет (порядок) применения правил: правило дифференцирования сложной функции применяется в последнюю очередь.

Желаю успехов!

Ответы:

Пример 2: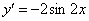 

Пример 4: 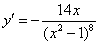  Указание: перед дифференцированием необходимо перенести степень наверх, сменив у показателя знак  .

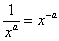Пример 5: