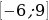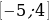"Производная в ЕГЭ"

Производная в ЕГЭ (база)

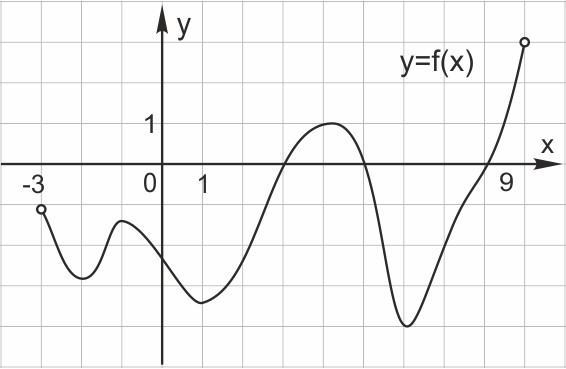
1. На рисунке 1 изображен график функции y=f(x), определенной на интервале (−3;9). Найдите количество точек, в которых производная функции f(x) равна 0.

Рисунок 1 Рисунок 2

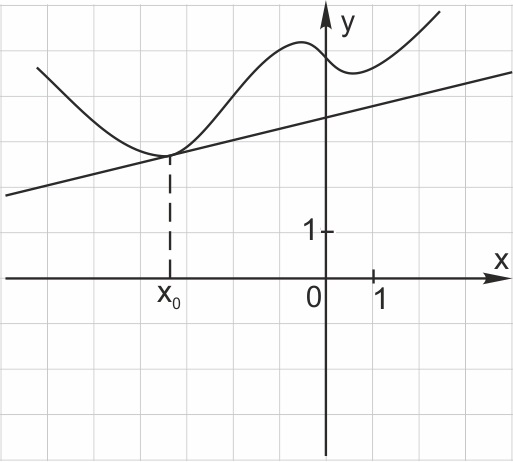
1. На рисунке 2 изображён график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке

Рисунок 3 Рисунок 4

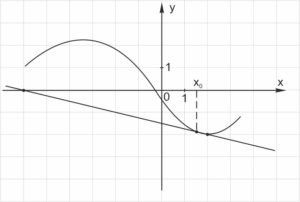
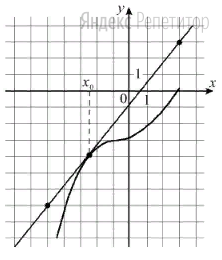
1. На рисунке 3 изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции y=f(x) в точке х0.

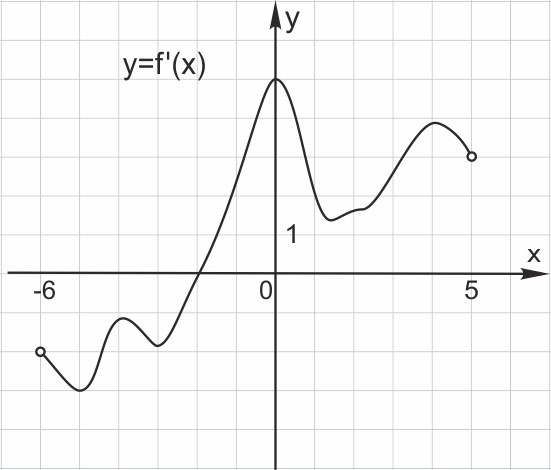
1. На рисунке 4 изображён график y=f′(x) — производной функции f(x), определённой на интервале (−6;5). В какой точке отрезка [−1;3] функция f(x) принимает наибольшее значение?

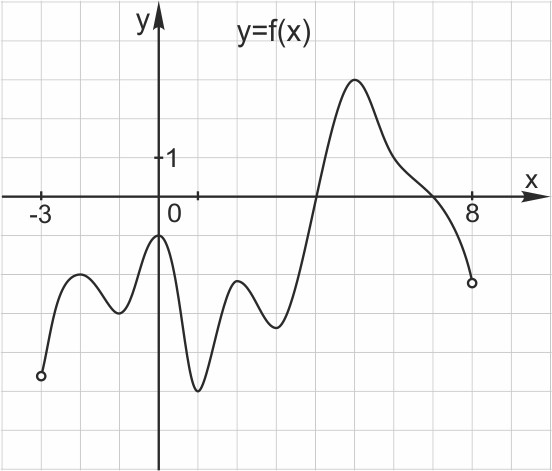
1. На рисунке 5 изображён график функции y=f(x), определённой на интервале (−3;8). Найдите количество точек, в которых касательная к графику функции параллельна прямой.

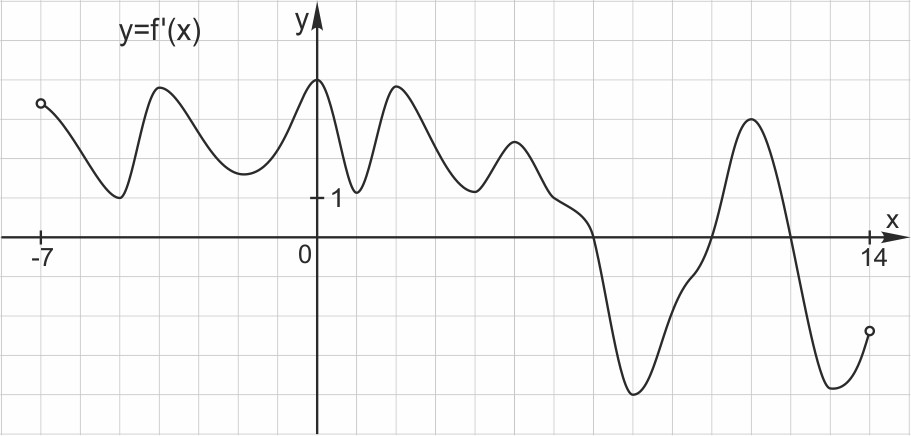
1. На рисунке 6 изображен график производной функции f(x), определенной на интервале (−7;14). Найдите количество точек максимума функции f(x) на отрезке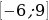 

Рисунок 5  Рисунок 6

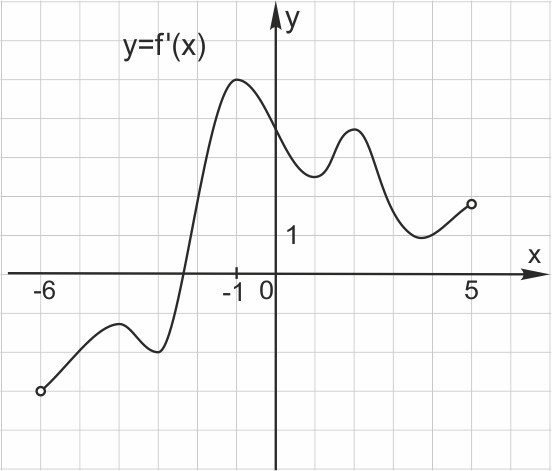
1. На рисунке 7 изображен график производной функции f(x), определенной на интервале (−6;5). Найдите точку экстремума функции f(x) на отрезке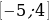 

Рисунок 7

1. Прямая y = − 4x − 11 является касательной к графику функции y = x3+ 7x2+ 7x − 6. Найдите абсциссу точки касания.

Производная в ЕГЭ (профиль)

1. На рисунке изображены график функции у=f(х) и касательная к нему в точке с абсциссой х₀. Найдите значение производной функции у=f(х)  в точке х₀

1. На рисунке изображен график у=f'(х) — производной функции f(х), определенной на интервале (−10;10).

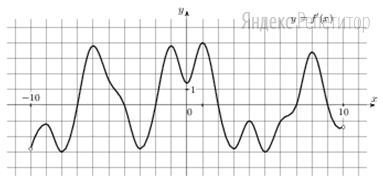
Найдите количество точек максимума функции у = f(х),  принадлежащих отрезку [−9;8].

1. На рисунке изображен график у=f'(х) — производной функции f(х), определенной на интервале (−1;10) .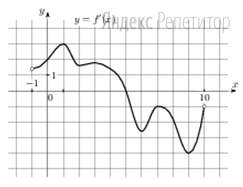

В какой точке отрезка [1; 5] функция у = f(х) принимает наименьшее значение?

1. На рисунке изображен график у=f'(х) — производной функции f(х), определенной на интервале (−11;3).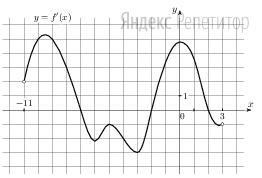

Найдите количество точек, в которых касательная к графику функции   у = f(х) параллельна прямой у=4х +10  или совпадает с ней.

1. На рисунке изображён график функции  у = f(х) и двенадцать точек на оси абсцисс: 

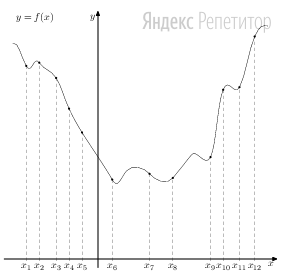
В скольких из этих точек производная функции  у = f(х) положительна?

1. На рисунке изображён график функции у = f(х). На оси абсцисс отмечены точки −2, −1, 2, 3.

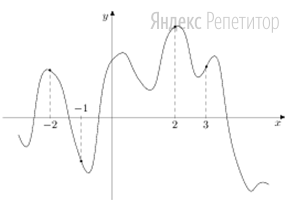
В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.