Частное образовательное учреждение
средняя общеобразовательная школа
«Царицынская №1»
ПРОМЕЖУТОЧНАЯ АТТЕСТАЦИЯ
ПО МАТЕМАТИКЕ
мини-ЕГЭ
10 класс
2014 – 2015 учебный год
Учебник: Алгебра и начала математического анализа. 10-11 классы. В 2 ч. Для учащихся общеобразовательных учреждений (базовый уровень)/ [А.Г. Мордкович и др.]; под ред. А.Г. Мордковича. – 10-е изд., стер. – М.: Мнемозина, 2009.
Геометрия. 10-11 классы: учеб.для общеобразоват. учреждений: базовый и профильный уровни/ [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.], – 17-е изд. - М.: Просвещение, 2008.
Интернет-ресурс: http://reshuege.ru/
Автор-составитель: учитель математики Шевченко Т.И.
Волгоград, 2015.
Вариант 1
1. Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 21 дня. В одной упаковке 10 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения?
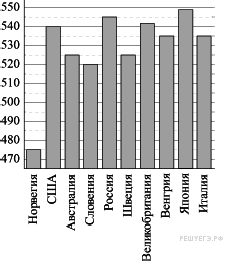
2. На диаграмме показан средний балл участников 10 стран в тестировании учащихся 4-го класса, по естествознанию в 2007 году (по 1000-балльной шкале). По данным диаграммы найдите число стран, в которых средний балл участников выше, чем в Венгрии.
3. От дома до дачи можно доехать на автобусе, на электричке или на маршрутном такси. В таблице показано время, которое нужно затратить на каждый участок пути. Какое наименьшее время потребуется на дорогу? Ответ дайте в часах.
| | 1 | 2 | 3 |
| Автобусом | От дома до автобусной
станции — 5 мин. | Автобус в пути:
2 ч 5 мин. | От остановки автобуса
до дачи пешком 10 мин. |
| Электричкой | От дома до станции железной
дороги — 30 мин. | Электричка в пути:
1 ч 40 мин. | От станции до дачи
пешком 5 мин. |
| Маршрутным такси | От дома до остановки маршрутного
такси — 20 мин. | Маршрутное такси в дороге:
1 ч 30 мин. | От остановки маршрутного такси
до дачи пешком 35 мин. |
4.  Найдите площадь прямоугольника, если его периметр равен 18, а отношение соседних сторон равно 1:2.
Найдите площадь прямоугольника, если его периметр равен 18, а отношение соседних сторон равно 1:2.
5. В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по неравенствам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам.
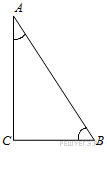
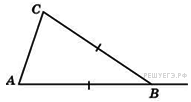
6. В треугольнике 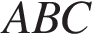 угол
угол 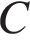 равен 90°,
равен 90°, 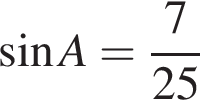 . Найдите
. Найдите  .
.
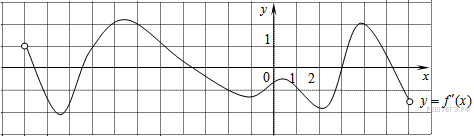
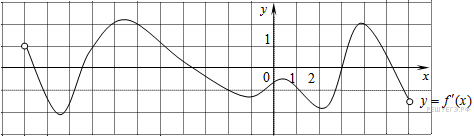
7. На рисунке изображен график функции 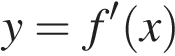 — производной функции f(x), определенной на интервале (−10; 6). В какой точке отрезка [−2; 4] функция f(x) принимает наименьшее значение?
— производной функции f(x), определенной на интервале (−10; 6). В какой точке отрезка [−2; 4] функция f(x) принимает наименьшее значение?
8. Площадь поверхности куба равна 18. Найдите его диагональ.
9. Найдите 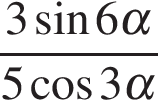 , если
, если 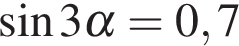 .
.
10. Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально и на исследуемом интервале температур определяется выражением 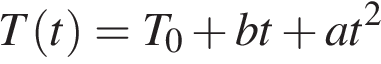 , где
, где 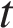 – время в минутах,
– время в минутах, 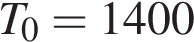 К,
К, 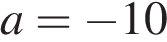 К/мин
К/мин ,
,  К/мин. Известно, что при температуре нагревателя свыше 1760 К прибор может испортиться, поэтому его нужно отключать. Определите, через какое наибольшее время после начала работы нужно отключать прибор. Ответ выразите в минутах.
К/мин. Известно, что при температуре нагревателя свыше 1760 К прибор может испортиться, поэтому его нужно отключать. Определите, через какое наибольшее время после начала работы нужно отключать прибор. Ответ выразите в минутах.
11.Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.
12. Первый и второй насосы наполняют бассейн за 9 минут, второй и третий — за 12 минут, а первый и третий — за 18 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?
13. Найдите наименьшее значение функции 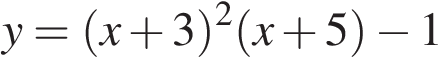 на отрезке
на отрезке 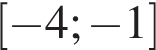 .
.
14. Решите систему уравнений 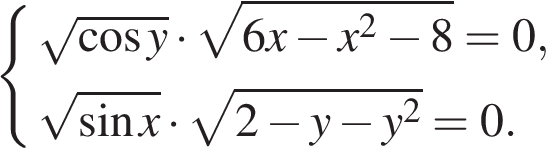
15. В правильной четырёхугольной пирамиде 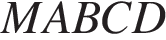 с вершиной
с вершиной 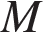 стороны основания равны
стороны основания равны 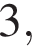 а боковые рёбра равны
а боковые рёбра равны 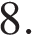 Найдите площадь сечения пирамиды плоскостью, проходящей через точку
Найдите площадь сечения пирамиды плоскостью, проходящей через точку 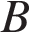 и середину ребра
и середину ребра 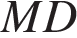 параллельно прямой
параллельно прямой 
Вариант 2
1. Магазин делает пенсионерам скидку на определенное количество процентов от цены покупки. Упаковка пельменей стоит в магазине 75 рублей. Пенсионер заплатил за упаковку пельменей 72 рубля. Сколько процентов составляет скидка для пенсионеров?
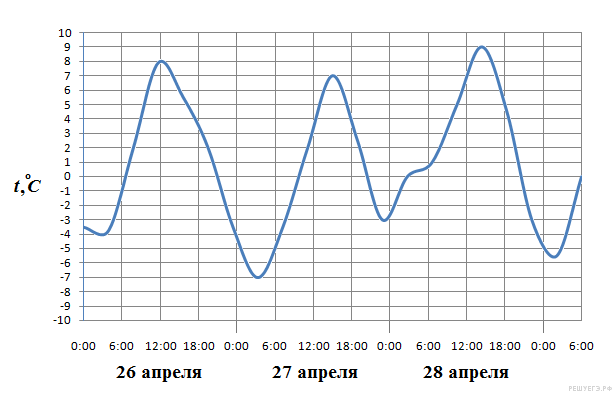
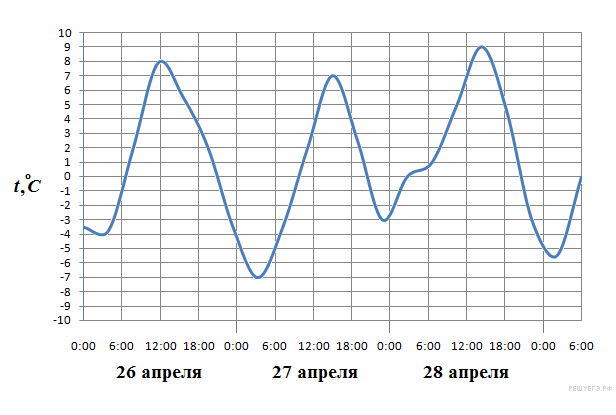
2. На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку наименьшую температуру воздуха 27 апреля. Ответ дайте в градусах Цельсия.
3. В таблице указаны средние цены (в рублях) на некоторые основные продукты питания в трех городах России (по данным на начало 2010 года).
| Наименование продукта | Петрозаводск | Павловск | Тверь |
| Пшеничный хлеб (батон) | 13 | 18 | 11 |
| Молоко (1 литр) | 26 | 28 | 26 |
| Картофель (1 кг) | 14 | 9 | 9 |
| Сыр (1 кг) | 230 | 240 | 240 |
| Мясо (говядина) | 280 | 275 | 280 |
| Подсолнечное масло (1 литр) | 38 | 38 | 38 |
Определите, в каком из этих городов окажется самым дешевым следующий набор продуктов: 2 батона пшеничного хлеба, 2 кг говядины, 1 л подсолнечного масла. В ответ запишите стоимость данного набора продуктов в этом городе (в рублях).
4. Точки O(0,0), 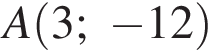 ,
, 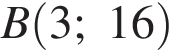 ,
, 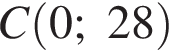 являются вершинами четырехугольника. Найдите ординату точки
являются вершинами четырехугольника. Найдите ординату точки 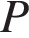 пересечения его диагоналей.
пересечения его диагоналей.
5. Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 7 очков в двух играх. Если команда выигрывает, она получает 6 очков, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,3.
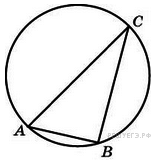
6. 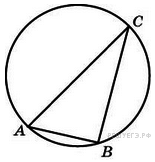 Угол
Угол 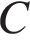 треугольника
треугольника 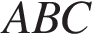 , вписанного в окружность радиуса 3, равен
, вписанного в окружность радиуса 3, равен  . Найдите сторону
. Найдите сторону 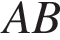 этого треугольника.
этого треугольника.
7. 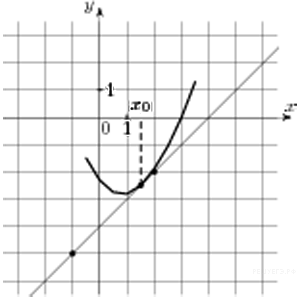 На рисунке изображён график функции
На рисунке изображён график функции 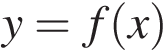 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой 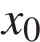 . Найдите значение производной функции
. Найдите значение производной функции 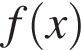 в точке
в точке 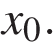
8. 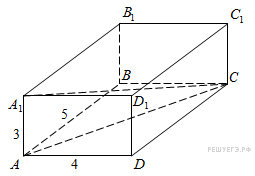 Найдите квадрат расстояния между вершинами C и A1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1=3.
Найдите квадрат расстояния между вершинами C и A1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1=3.
9. Найдите значение выражения 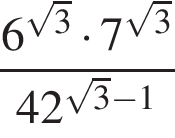 .
.
10. Скейтбордист прыгает на стоящую на рельсах платформу, со скоростью  м/с под острым углом
м/с под острым углом  к рельсам. От толчка платформа начинает ехать со скоростью
к рельсам. От толчка платформа начинает ехать со скоростью 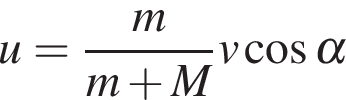 (м/с), где
(м/с), где  кг – масса скейтбордиста со скейтом, а
кг – масса скейтбордиста со скейтом, а  кг – масса платформы. Под каким максимальным углом
кг – масса платформы. Под каким максимальным углом  (в градусах) нужно прыгать, чтобы разогнать платформу не менее чем до 0,25 м/с?.
(в градусах) нужно прыгать, чтобы разогнать платформу не менее чем до 0,25 м/с?.
11. Найдите объем правильной шестиугольной призмы, все ребра которой равны  .
.
12. Смешали некоторое количество 15–процентного раствора некоторого вещества с таким же количеством 19–процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
13. Найдите наименьшее значение функции на отрезке  .
.
14. а) Решите уравнение
б)Найдите все корни этого уравнения, принадлежащие промежутку
15. Радиус основания конуса с вершиной P равен 6, а длина его образующей равна 9. На окружности основания конуса выбраны точки A и B, делящие окружность на две дуги, длины которых относятся как 1:3. Найдите площадь сечения конуса плоскостью ABP.
Вариант 3
1. Оптовая цена учебника 170 рублей. Розничная цена на 20% выше оптовой. Какое наибольшее число таких учебников можно купить по розничной цене на 7000 рублей?
2. На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру во второй половине 1973 года. Ответ дайте в градусах Цельсия.
3. Семья из трех человек едет из Москвы в Чебоксары. Можно ехать поездом, а можно — на своей машине. Билет на поезд на одного человека стоит 930 рублей. Автомобиль расходует 11 литров бензина на 100 километров пути, расстояние по шоссе равно 700 км, а цена бензина равна 18,5 рублей за литр. Сколько рублей придется заплатить за наиболее дешевую поездку на троих?
4.

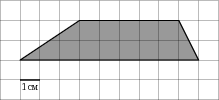
На клетчатой бумаге с клетками размером 1 см  1 см изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
1 см изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
5. За круглый стол на 17 стульев в случайном порядке рассаживаются 15 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.
6. Одна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий этой стороне. Ответ дайте в градусах
7.
На рисунке изображен график производной функции f(x), определенной на интервале (−6; 5). Найдите точку экстремума функции f(x) на отрезке [−5; 4].
8. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.
9. Найдите значение выражения , если .
10. Трактор тащит сани с силой  кН, направленной под острым углом
кН, направленной под острым углом  к горизонту. Мощность (в киловаттах) трактора при скорости
к горизонту. Мощность (в киловаттах) трактора при скорости  м/с равна . При каком максимальном угле
м/с равна . При каком максимальном угле  (в градусах) эта мощность будет не менее 75 кВт?
(в градусах) эта мощность будет не менее 75 кВт?
11. В правильной шестиугольной призме все ребра равны 1. Найдите тангенс угла
12 Клиент А. сделал вклад в банке в размере 6200 рублей. Проценты по вкладу начисляются раз в год и прибавляются к текущей сумме вклада. Ровно через год на тех же условиях такой же вклад в том же банке сделал Б. Ещё ровно через год клиенты А. и Б. закрыли вклады и забрали все накопившиеся деньги. При этом клиент А. получил на 682 рубля больше клиента Б.Какой процент годовых начислял банк по этим вкладам?
13. Найдите наибольшее значение функции на отрезке  .
.
14. а) Решите уравнение
б) Укажите корни уравнения, принадлежащие отрезку
15. Дана правильная четырехугольная пирамида Боковое ребро сторона основания равна  . Найдите расстояние от точки
. Найдите расстояние от точки  до плоскости где
до плоскости где 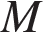 — середина ребра
— середина ребра 
Вариант 4
1. В летнем лагере на каждого участника полагается 30 г сахара в день. В лагере 103 человека. Сколько килограммовых упаковок сахара понадобится на весь лагерь на 6 дней?
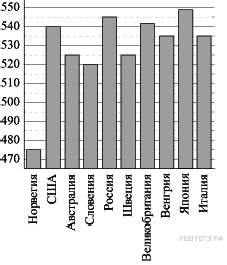
2. На диаграмме показан средний балл участников 10 стран в тестировании учащихся 8-го класса по математике в 2007 году (по 1000-балльной шкале). Найдите средний балл участников из Болгарии.
3. Для изготовления книжных полок требуется заказать 48 одинаковых стекол в одной из трех фирм. Площадь каждого стекла 0,25  . В таблице приведены цены на стекло, а также на резку стекол и шлифовку края. Сколько рублей будет стоить самый дешевый заказ?
. В таблице приведены цены на стекло, а также на резку стекол и шлифовку края. Сколько рублей будет стоить самый дешевый заказ?
| Фирма | Цена стекла (руб. за 1 м2) | Резка и шлифовка (руб. за одно стекло) |
| A | 420 | 75 |
| Б | 440 | 65 |
| В | 470 | 55 |
4. В треугольнике 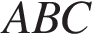 . Внешний угол при вершине
. Внешний угол при вершине 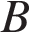 равен . Найдите угол
равен . Найдите угол 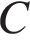 . Ответ дайте в градусах.
. Ответ дайте в градусах.
5. Конкурс исполнителей проводится в 5 дней. Всего заявлено 65 выступлений — по одному от каждой страны. В первый день 13 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?
6. В треугольнике 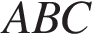 угол
угол  равен 90°, . Найдите
равен 90°, . Найдите  .
.
7.
На рисунке изображен график функции y=f(x), определенной на интервале (−1; 12). Определите количество целых точек, в которых производная функции отрицательна.
8. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
9. Найдите  , если .
, если .
10. Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объeм и давление связаны соотношением , где  (атм.) – давление в газе,
(атм.) – давление в газе,  – объeм газа в литрах. Изначально объeм газа равен 1,6 л, а его давление равно одной атмосфере. В соответствии с техническими характеристиками поршень насоса выдерживает давление не более 128 атмосфер. Определите, до какого минимального объeма можно сжать газ. Ответ выразите в литрах.
– объeм газа в литрах. Изначально объeм газа равен 1,6 л, а его давление равно одной атмосфере. В соответствии с техническими характеристиками поршень насоса выдерживает давление не более 128 атмосфер. Определите, до какого минимального объeма можно сжать газ. Ответ выразите в литрах.
11. В правильной шестиугольной призме все ребра равны 1. Найдите тангенс угла 
12. Из одной точки кольцевой дороги, длина которой равна 12 км, одновременно в одном направлении выехали два автомобиля. Скорость первого автомобиля равна 101 км/ч, и через 20 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
13. Найдите наибольшее значение функции на отрезке .
14. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
15. В правильной четырёхугольной пирамиде SABCD точка S — вершина. Точка M — середина ребра SA, точка K — середина ребра SC. Найдите угол между плоскостями BMK и ABC, если AB=8, SC=10.







 Найдите площадь прямоугольника, если его периметр равен 18, а отношение соседних сторон равно 1:2.
Найдите площадь прямоугольника, если его периметр равен 18, а отношение соседних сторон равно 1:2.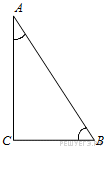
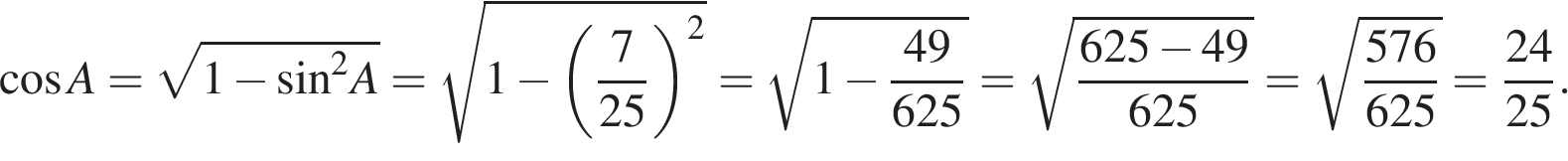
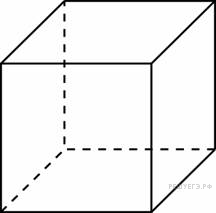 Площадь поверхности куба равна 18. Найдите его диагональ.
Площадь поверхности куба равна 18. Найдите его диагональ.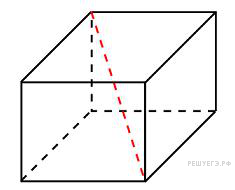 Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.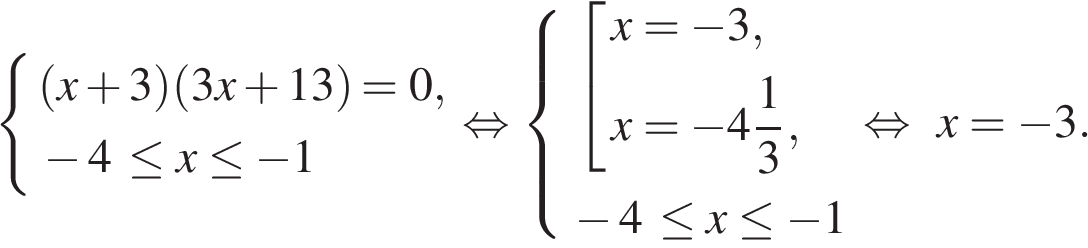
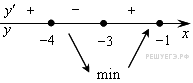
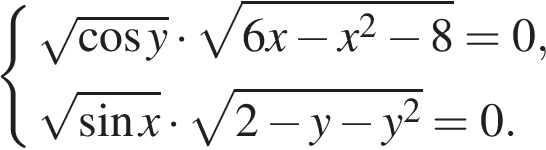
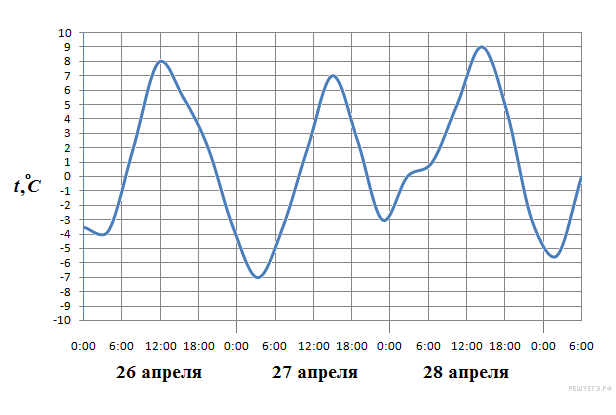
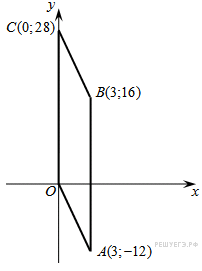 Найдём длины сторон четырёхугольника:
Найдём длины сторон четырёхугольника:
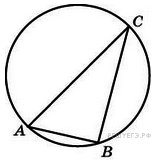 Угол
Угол 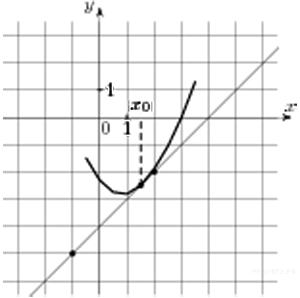 На рисунке изображён график функции
На рисунке изображён график функции 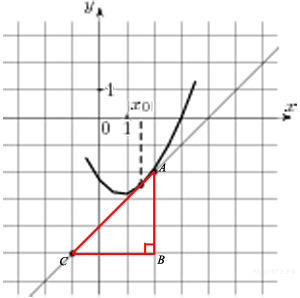 Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (2; −2), B (2; −5), C(−1; −5). Тангенс угла наклона касательной к оси абсцисс будет равен тангенсу угла ACB:
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (2; −2), B (2; −5), C(−1; −5). Тангенс угла наклона касательной к оси абсцисс будет равен тангенсу угла ACB: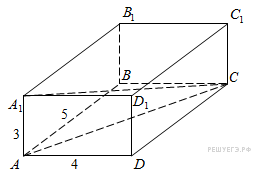 Найдите квадрат расстояния между вершинами C и A1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1=3.
Найдите квадрат расстояния между вершинами C и A1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1=3.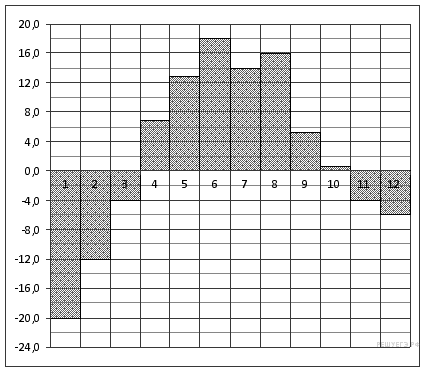
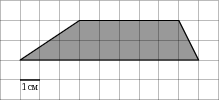 На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см 
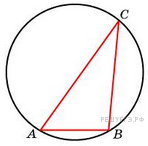 Одна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий этой стороне. Ответ дайте в градусах
Одна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий этой стороне. Ответ дайте в градусах
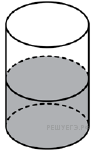 В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр основания которого в 2 раза больше диаметра основания первого? Ответ выразите в см.
В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр основания которого в 2 раза больше диаметра основания первого? Ответ выразите в см.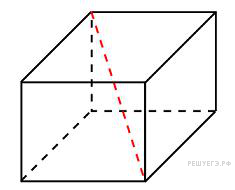 Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.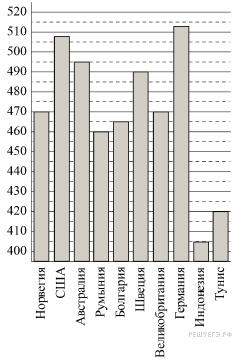
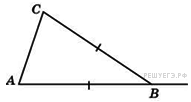 В треугольнике
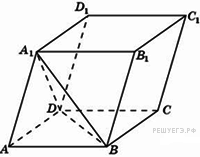
В треугольнике 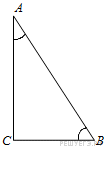 Имеем:
Имеем: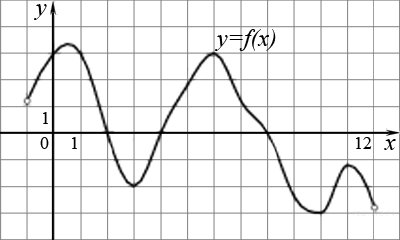
 Объем параллелепипеда
Объем параллелепипеда 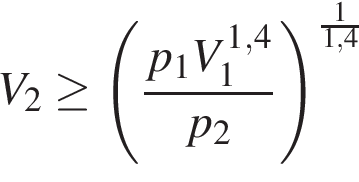 , где
, где 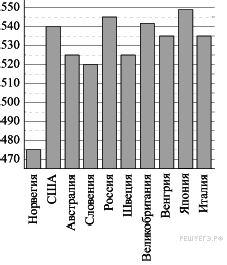
 Найдите площадь прямоугольника, если его периметр равен 18, а отношение соседних сторон равно 1:2.
Найдите площадь прямоугольника, если его периметр равен 18, а отношение соседних сторон равно 1:2.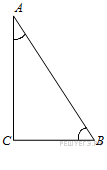
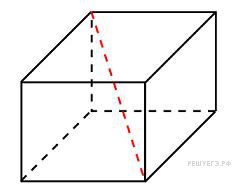 Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.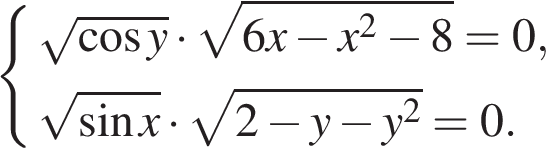
 Угол
Угол 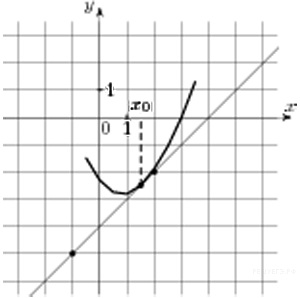 На рисунке изображён график функции
На рисунке изображён график функции 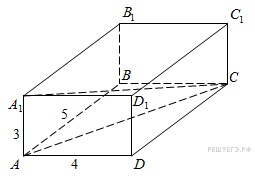 Найдите квадрат расстояния между вершинами C и A1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1=3.
Найдите квадрат расстояния между вершинами C и A1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1=3.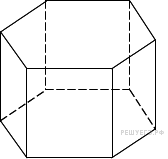 Найдите объем правильной шестиугольной призмы, все ребра которой равны
Найдите объем правильной шестиугольной призмы, все ребра которой равны 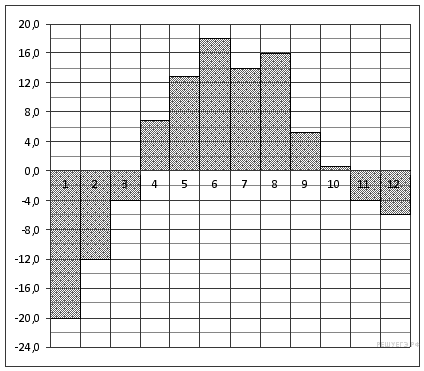
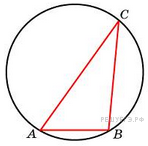 Одна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий этой стороне. Ответ дайте в градусах
Одна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий этой стороне. Ответ дайте в градусах
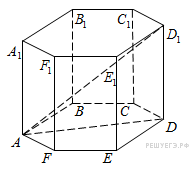 В правильной шестиугольной призме
В правильной шестиугольной призме 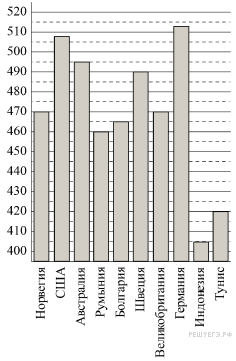
 В треугольнике
В треугольнике 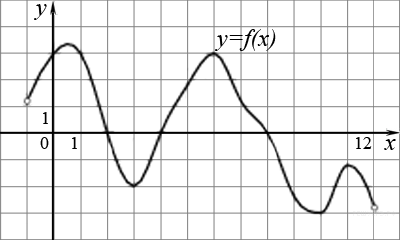
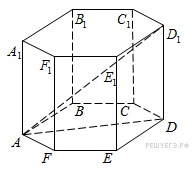 В правильной шестиугольной призме
В правильной шестиугольной призме 
 Найдите площадь прямоугольника, если его периметр равен 18, а отношение соседних сторон равно 1:2.
Найдите площадь прямоугольника, если его периметр равен 18, а отношение соседних сторон равно 1:2.

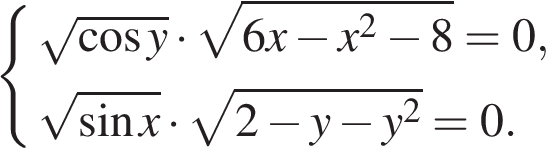

 Угол
Угол  На рисунке изображён график функции
На рисунке изображён график функции  Найдите квадрат расстояния между вершинами C и A1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1=3.
Найдите квадрат расстояния между вершинами C и A1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1=3.









